10.1: A elipse
- Page ID
- 189342
- Escreva equações de elipses na forma padrão.
- Elipses gráficas centradas na origem.
- Elipses gráficas não centradas na origem.
- Resolva problemas aplicados envolvendo elipses.
Você consegue se imaginar em uma extremidade de uma sala grande e ainda ouvir um sussurro de uma pessoa parada do outro lado? O National Statuary Hall em Washington, D.C., mostrado na Figura\(\PageIndex{1}\), é uma dessas salas. É uma sala de formato oval chamada câmara sussurrante porque a forma possibilita que o som viaje pelas paredes. Nesta seção, investigaremos a forma desta sala e suas aplicações no mundo real, incluindo a distância entre duas pessoas no Statuary Hall e ainda ouvirem uma à outra sussurrar.

Figura\(\PageIndex{1}\): O National Statuary Hall em Washington, D.C. (crédito: Greg Palmer, Flickr)
Escrevendo equações de elipses na forma padrão
Uma seção cônica, ou cônica, é uma forma resultante da interseção de um cone circular reto com um plano. O ângulo no qual o plano cruza o cone determina a forma, conforme mostrado na Figura\(\PageIndex{2}\).
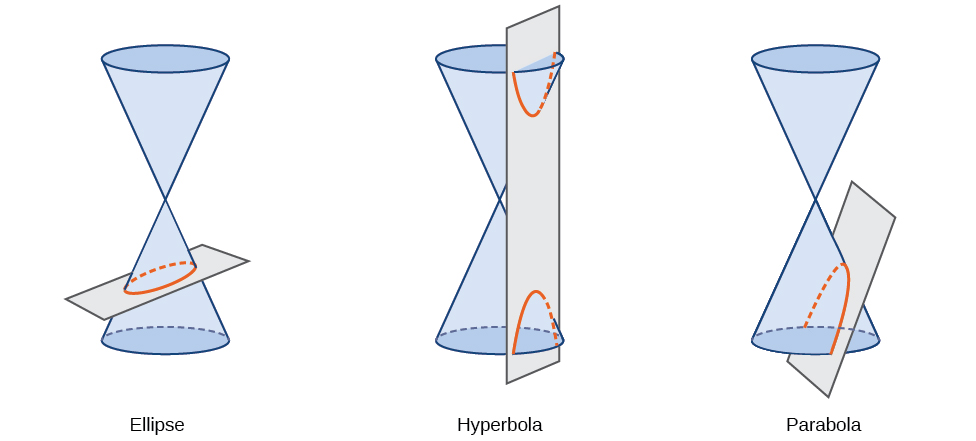
Figura\(\PageIndex{2}\)
As seções cônicas também podem ser descritas por um conjunto de pontos no plano coordenado. Mais adiante neste capítulo, veremos que o gráfico de qualquer equação quadrática em duas variáveis é uma seção cônica. Os sinais das equações e os coeficientes dos termos variáveis determinam a forma. Esta seção se concentra nas quatro variações da forma padrão da equação da elipse. Uma elipse é o conjunto de todos os pontos\((x,y)\) em um plano de forma que a soma de suas distâncias de dois pontos fixos seja uma constante. Cada ponto fixo é chamado de foco (plural: focos).
Podemos desenhar uma elipse usando um pedaço de papelão, duas tachinhas, um lápis e um barbante. Coloque as tachinhas no papelão para formar os focos da elipse. Corte um pedaço de barbante maior do que a distância entre as duas tachinhas (o comprimento da corda representa a constante na definição). Prenda cada extremidade da corda no papelão e trace uma curva com um lápis esticado contra a corda. O resultado é uma elipse. Veja a Figura\(\PageIndex{3}\).
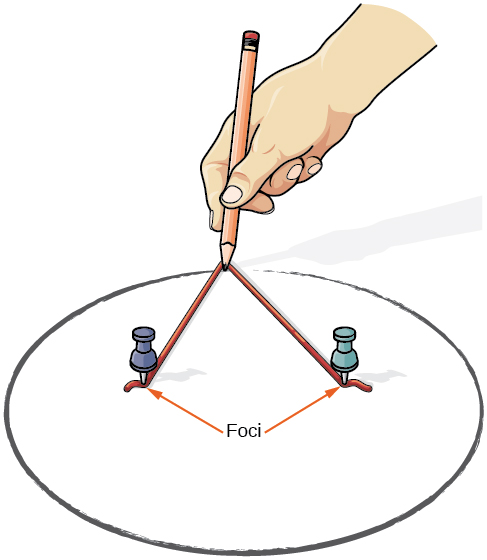
Figura\(\PageIndex{3}\)
Cada elipse tem dois eixos de simetria. O eixo mais longo é chamado de eixo maior e o eixo mais curto é chamado de eixo menor. Cada extremidade do eixo maior é o vértice da elipse (plural: vértices), e cada extremidade do eixo menor é um co-vértice da elipse. O centro de uma elipse é o ponto médio dos eixos maior e menor. Os eixos são perpendiculares no centro. Os focos sempre estão no eixo maior, e a soma das distâncias dos focos a qualquer ponto da elipse (a soma constante) é maior que a distância entre os focos (Figura\(\PageIndex{4}\)).
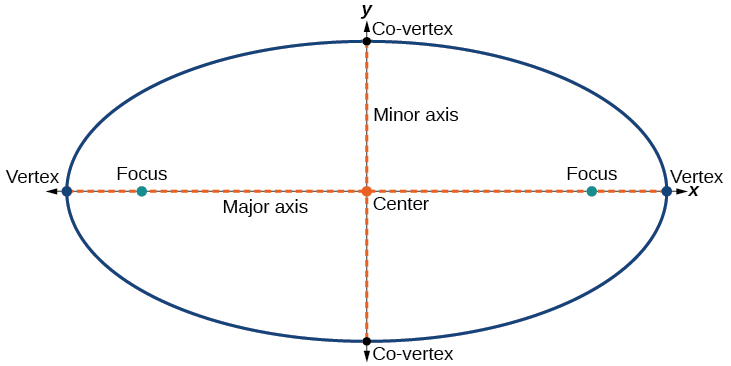
Figura\(\PageIndex{4}\)
Nesta seção, restringimos as elipses àquelas que estão posicionadas vertical ou horizontalmente no plano coordenado. Ou seja, os eixos ficarão sobre ou ficarão paralelos aos\(y\) eixos\(x\) - e -. Mais adiante no capítulo, veremos elipses que são giradas no plano coordenado.
Para trabalhar com elipses horizontais e verticais no plano coordenado, consideramos dois casos: aqueles que estão centrados na origem e aqueles que estão centrados em um ponto diferente da origem. Primeiro, aprenderemos a derivar as equações das elipses e, em seguida, aprenderemos como escrever as equações das elipses na forma padrão. Posteriormente, usaremos o que aprendemos para desenhar os gráficos.
Derivando a equação de uma elipse centrada na origem
Para derivar a equação de uma elipse centrada na origem, começamos com os focos\((−c,0)\)\((c,0)\) e. A elipse é o conjunto de todos os pontos de\((x,y)\) forma que a soma das distâncias\((x,y)\) até os focos seja constante, conforme mostrado na Figura\(\PageIndex{5}\).
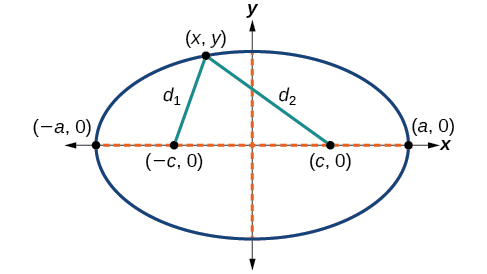
Figura\(\PageIndex{5}\)
Se\((a,0)\) for um vértice da elipse, a distância de\((−c,0)\) até\((a,0)\) é\(a−(−c)=a+c\). A distância de\((c,0)\) para\((a,0)\) é\(a−c\). A soma das distâncias dos focos ao vértice é
\((a+c)+(a−c)=2a\)
Se\((x,y)\) for um ponto na elipse, então podemos definir as seguintes variáveis:
- \(d_1=\)a distância de\((−c,0)\) até\((x,y)\)
- \(d_2=\)a distância de\((c,0)\) até\((x,y)\)
Pela definição de uma elipse,\(d_1+d_2\) é constante para qualquer ponto\((x,y)\) na elipse. Sabemos que a soma dessas distâncias é\(2a\) para o vértice\((a,0)\). Isso se segue\(d_1+d_2=2a\) para qualquer ponto da elipse. Começaremos a derivação aplicando a fórmula da distância. O resto da derivação é algébrica.
\[\begin{align*} d_1+d_2&= 2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}+\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance formula}\\ \sqrt{{(x+c)}^2+y^2}+\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a-\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={\left[2a-\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2-4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining squares.}\\ 2cx&=4a^2-4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=-4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=-a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {\left[ cx-a^2\right]}^2&=a^2{\left[ \sqrt{{(x-c)}^2+y^2}\right] }^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^2x^2-c^2x^2+a^2y^2&=a^4-a^2c^2\qquad \text{Rewrite.}\\ x^2(a^2-c^2)+a^2y^2&=a^2(a^2-c^2)\qquad \text{Factor common terms.}\\ x^2b^2+a^2y^2&=a^2b^2\qquad \text{Set } b^2=a^2-c^2\\ \dfrac{x^2b^2}{a^2b^2}+\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}&=1\qquad \text{Simplify} \end{align*}\]
Assim, a equação padrão de uma elipse é\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) .Essa equação define uma elipse centrada na origem. Se\(a>b\), a elipse for esticada ainda mais na direção horizontal e, se\(b>a\), a elipse for esticada ainda mais na direção vertical.
Escrevendo equações de elipses centradas na origem na forma padrão
As formas padrão de equações nos informam sobre as principais características dos gráficos. Reserve um momento para relembrar algumas das formas padrão de equações com as quais trabalhamos no passado: linear, quadrática, cúbica, exponencial, logarítmica e assim por diante. Ao aprender a interpretar formas padrão de equações, estamos estabelecendo uma ponte entre representações algébricas e geométricas de fenômenos matemáticos.
As principais características da elipse são seu centro, vértices, co-vértices, focos e comprimentos e posições dos eixos maior e menor. Assim como com outras equações, podemos identificar todas essas características apenas observando a forma padrão da equação. Há quatro variações da forma padrão da elipse. Essas variações são categorizadas primeiro pela localização do centro (a origem ou não a origem) e depois pela posição (horizontal ou vertical). Cada um é apresentado junto com uma descrição de como as partes da equação se relacionam com o gráfico. Interpretar essas partes nos permite formar uma imagem mental da elipse.
A forma padrão da equação de uma elipse com centro\((0,0)\) e eixo maior no\(x\) eixo -é
\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\]
onde
- \(a>b\)
- o comprimento do eixo principal é\(2a\)
- as coordenadas dos vértices são\((\pm a,0)\)
- o comprimento do eixo menor é\(2b\)
- as coordenadas dos co-vértices são\((0,\pm b)\)
- as coordenadas dos focos são\((\pm c,0)\), onde\(c^2=a^2−b^2\). Veja a Figura\(\PageIndex{6a}\).
A forma padrão da equação de uma elipse com centro\((0,0)\) e eixo maior no\(y\) eixo -é
\[\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\]
onde
- \(a>b\)
- o comprimento do eixo principal é\(2a\)
- as coordenadas dos vértices são\((0,\pm a)\)
- o comprimento do eixo menor é\(2b\)
- as coordenadas dos co-vértices são\((\pm b,0)\)
- as coordenadas dos focos são\((0,\pm c)\), onde\(c^2=a^2−b^2\). Veja a Figura\(\PageIndex{6b}\).
Observe que os vértices, co-vértices e focos estão relacionados pela equação\(c^2=a^2−b^2\). Quando recebemos as coordenadas dos focos e vértices de uma elipse, podemos usar essa relação para encontrar a equação da elipse na forma padrão.
Figura\(\PageIndex{6}\): (a) Elipse horizontal com centro\((0,0)\) (b) Elipse vertical com centro\((0,0)\)
- Determine se o eixo principal está no eixo x ou y.
- Se as coordenadas dadas dos vértices e focos tiverem a forma\((\pm a,0)\) e\((\pm c,0)\) respectivamente, o eixo principal será o eixo x. Use o formulário padrão\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
- Se as coordenadas dadas dos vértices e focos tiverem a forma\((0,\pm a)\) e\((\pm c,0)\), respectivamente, o eixo principal será o eixo y. Use o formulário padrão\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
- Use a equação\(c^2=a^2−b^2\), junto com as coordenadas dadas dos vértices e focos, para resolver\(b^2\).
- Substitua os valores por\(a^2\) e\(b^2\) na forma padrão da equação determinada na Etapa 1.
Qual é a equação de forma padrão da elipse que tem vértices\((\pm 8,0)\) e focos\((\pm 5,0)\)?
Solução
Os focos estão no\(x\) eixo -, então o eixo principal é o\(x\) eixo -. Assim, a equação terá a forma\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Os vértices são\((\pm 8,0)\), então\(a=8\)\(a^2=64\) e.
Os focos são\((\pm 5,0)\), então\(c=5\)\(c^2=25\) e.
Sabemos que os vértices e focos estão relacionados pela equação\(c^2=a^2−b^2\). Resolvendo para\(b^2\), temos:
\[\begin{align*} c^2&=a^2-b^2\\ 25&=64-b^2\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=39\qquad \text{Solve for } b^2 \end{align*}\]
Agora precisamos apenas substituir\(a^2=64\) e\(b^2=39\) entrar na forma padrão da equação. A equação da elipse é\(\dfrac{x^2}{64}+\dfrac{y^2}{39}=1\).
Qual é a equação de forma padrão da elipse que tem vértices\((0,\pm 4)\) e focos\((0,\pm \sqrt{15})\)?
- Resposta
-
\(x^2+\dfrac{y^2}{16}=1\)
Podemos escrever a equação de uma elipse centrada na origem dadas as coordenadas de apenas um foco e vértice?
Sim. As elipses são simétricas, então as coordenadas dos vértices de uma elipse centrada em torno da origem sempre terão a forma\((\pm a,0)\) ou\((0, \pm a)\). Da mesma forma, as coordenadas dos focos sempre terão a forma\((\pm c,0)\) ou\((0, \pm c)\). Sabendo disso, podemos usar\(a\) e a\(c\) partir dos pontos dados, junto com a equação\(c^2=a^2−b^2\), para encontrar\(b^2\).
Escrevendo equações de elipses não centradas na origem
Como os gráficos de outras equações, o gráfico de uma elipse pode ser traduzido. Se uma elipse for traduzida em\(h\) unidades horizontalmente e\(k\) unidades verticalmente, o centro da elipse será\((h,k)\). Essa tradução resulta na forma padrão da equação que vimos anteriormente, com\(x\) substituído por\((x−h)\) e y substituído por\((y−k)\).
A forma padrão da equação de uma elipse com centro\((h, k)\) e eixo maior paralelos ao\(x\) eixo -é
\[\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\]
onde
- \(a>b\)
- o comprimento do eixo principal é\(2a\)
- as coordenadas dos vértices são\((h\pm a,k)\)
- o comprimento do eixo menor é\(2b\)
- as coordenadas dos co-vértices são\((h,k\pm b)\)
- as coordenadas dos focos são\((h\pm c,k)\), onde\(c^2=a^2−b^2\). Veja a Figura\(\PageIndex{7a}\).
A forma padrão da equação de uma elipse com centro\((h,k)\) e eixo maior paralelos ao\(y\) eixo -é
\[\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\]
onde
- \(a>b\)
- o comprimento do eixo principal é\(2a\)
- as coordenadas dos vértices são\((h,k\pm a)\)
- o comprimento do eixo menor é\(2b\)
- as coordenadas dos co-vértices são\((h\pm b,k)\)
- as coordenadas dos focos são\((h,k\pm c)\), onde\(c^2=a^2−b^2\). Veja a Figura\(\PageIndex{7b}\).
Assim como as elipses centradas na origem, as elipses centradas em um ponto\((h,k)\) têm vértices, co-vértices e focos relacionados pela equação\(c^2=a^2−b^2\). Podemos usar essa relação junto com as fórmulas do ponto médio e da distância para encontrar a equação da elipse na forma padrão quando os vértices e focos são fornecidos.
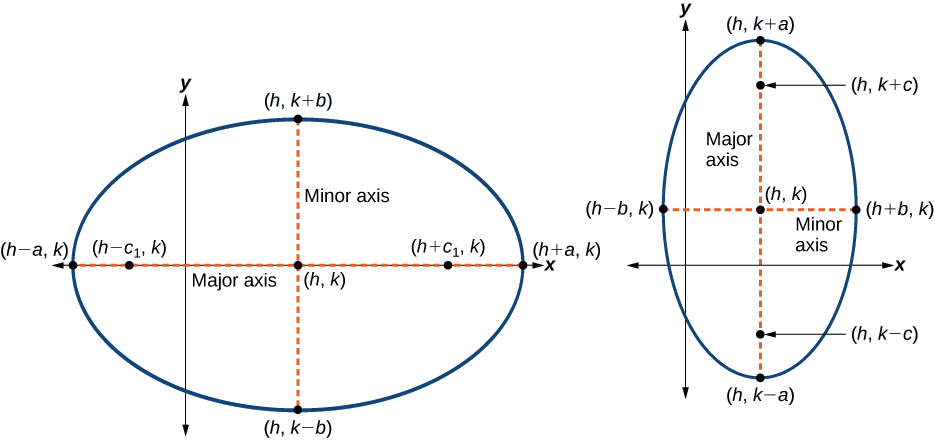
Figura\(\PageIndex{7}\): (a) Elipse horizontal com centro\((h,k)\) (b) Elipse vertical com centro\((h,k)\)
- Determine se o eixo principal é paralelo ao\(y\) eixo\(x\) - ou -.
- Se as coordenadas y dos vértices e focos fornecidos forem as mesmas, o eixo maior será paralelo ao\(x\) eixo y. Use o formulário padrão\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\)
- Se as coordenadas x dos vértices e focos fornecidos forem as mesmas, o eixo maior será paralelo ao eixo y. Use o formulário padrão\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\)
- Identifique o centro da elipse\((h,k)\) usando a fórmula do ponto médio e as coordenadas dadas para os vértices.
- \(a^2\)Determine resolvendo o comprimento do eixo principal,\(2a\), que é a distância entre os vértices fornecidos.
- Encontre\(c^2\) usando\(h\) e\(k\), encontrado na Etapa 2, junto com as coordenadas fornecidas para os focos.
- Resolva o\(b^2\) uso da equação\(c^2=a^2−b^2\).
- Substitua os valores por\(h\)\(k\)\(a^2\),, e\(b^2\) na forma padrão da equação determinada na Etapa 1.
Qual é a equação da forma padrão da elipse que tem vértices\((−2,−8)\)\((−2,2)\) e focos\((−2,−7)\) e\((−2,1)\)?
Solução
As\(x\) coordenadas -dos vértices e focos são as mesmas, então o eixo maior é paralelo ao\(y\) eixo -. Assim, a equação da elipse terá a forma
\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1 \nonumber\)
Primeiro, identificamos o centro,\((h,k)\). O centro está a meio caminho entre os vértices,\((−2,−8)\)\((−2,2)\) e. Aplicando a fórmula do ponto médio, temos:
\[\begin{align} (h,k) &=\left(\dfrac{−2+(−2)}{2},\dfrac{−8+2}{2}\right) \nonumber \\ &=(−2,−3) \nonumber \end{align} \nonumber\]
Em seguida, encontramos\(a^2\). O comprimento do eixo principal,\(2a\), é limitado pelos vértices. Resolvemos para\(a\) encontrando a distância entre as coordenadas y dos vértices.
\[\begin{align} 2a &=2−(−8) \nonumber \\ 2a &=10 \nonumber\\ a&=5 \nonumber \end{align} \nonumber\]
Então\(a^2=25\).
Agora encontramos\(c^2\). Os focos são dados por\((h,k\pm c)\). Então,\((h,k−c)=(−2,−7)\)\((h,k+c)=(−2,1)\) e. Substituímos\(k=−3\) usando qualquer um desses pontos para resolver\(c\).
\[\begin{align} k+c &=1 \nonumber \\ −3+c&=1 \nonumber \\ c&=4 \nonumber \end{align} \nonumber\]
Então\(c^2=16\).
Em seguida, resolvemos o\(b^2\) uso da equação\(c^2=a^2−b^2\).
\[\begin{align} c^2&=a^2−b^2 \nonumber \\ 16&=25−b^2 \nonumber \\ b^2&=9 \nonumber \end{align} \nonumber\]
Finalmente, substituímos os valores encontrados por\(h\),\(k\)\(a^2\), e\(b^2\) na equação de forma padrão por uma elipse:
\[\dfrac{{(x+2)}^2}{9}+\dfrac{{(y+3)}^2}{25}=1 \nonumber\]
Qual é a equação da forma padrão da elipse que tem vértices\((−3,3)\)\((5,3)\) e focos\((1−2\sqrt{3},3)\) e\((1+2\sqrt{3},3)\)?
- Resposta
-
\(\dfrac{{(x−1)}^2}{16}+\dfrac{{(y−3)}^2}{4}=1 \nonumber\)
Representação gráfica de elipses centradas na origem
Assim como podemos escrever a equação para uma elipse dado seu gráfico, podemos representar graficamente uma elipse dada sua equação. Para representar graficamente elipses centradas na origem, usamos a forma padrão
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1, a>b\)para elipses horizontais
e
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1, a>b\)para elipses verticais
- Use as formas padrão das equações de uma elipse para determinar o eixo principal, os vértices, os co-vértices e os focos.
- Se a equação estiver na forma\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), onde\(a>b\), então
- o eixo principal é o\(x\) eixo -
- as coordenadas dos vértices são\((\pm a,0)\)
- as coordenadas dos co-vértices são\((0,\pm b)\)
- as coordenadas dos focos são\((\pm c,0)\)
- Se a equação estiver na forma\(x^2b^2+y^2a^2=1\), onde\(a>b\), então
- o eixo principal é o\(y\) eixo -
- as coordenadas dos vértices são\((0,\pm a)\)
- as coordenadas dos co-vértices são\((\pm b,0)\)
- as coordenadas dos focos são\((0,\pm c)\)
- Se a equação estiver na forma\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), onde\(a>b\), então
- Resolva o\(c\) uso da equação\(c^2=a^2−b^2\).
- Faça um gráfico do centro, vértices, co-vértices e focos no plano coordenado e desenhe uma curva suave para formar a elipse.
Faça um gráfico da elipse dada pela equação,\(\dfrac{x^2}{9}+\dfrac{y^2}{25}=1\). Identifique e rotule o centro, os vértices, os co-vértices e os focos.
Solução
Primeiro, determinamos a posição do eixo principal. Porque\(25>9\), o eixo principal está no\(y\) eixo -. Portanto, a equação está na forma\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\), onde\(b^2=9\)\(a^2=25\) e. Daqui resulta que:
- o centro da elipse é\((0,0)\)
- as coordenadas dos vértices são\((0,\pm a)=(0,\pm \sqrt{25})=(0,\pm 5)\)
- as coordenadas dos co-vértices são\((\pm b,0)=(\pm 9,0)=(\pm 3,0)\)
- as coordenadas dos focos são\((0,\pm c)\), onde\(c^2=a^2−b^2\) Resolvendo para\(c\), temos:
\[\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−9} \nonumber\\ &=\pm \sqrt{16} \nonumber\\ &=\pm 4 \nonumber \end{align} \nonumber\]
Portanto, as coordenadas dos focos são\((0,\pm 4)\).
Em seguida, traçamos e rotulamos o centro, os vértices, os co-vértices e os focos e desenhamos uma curva suave para formar a elipse. Veja a Figura\(\PageIndex{8}\).
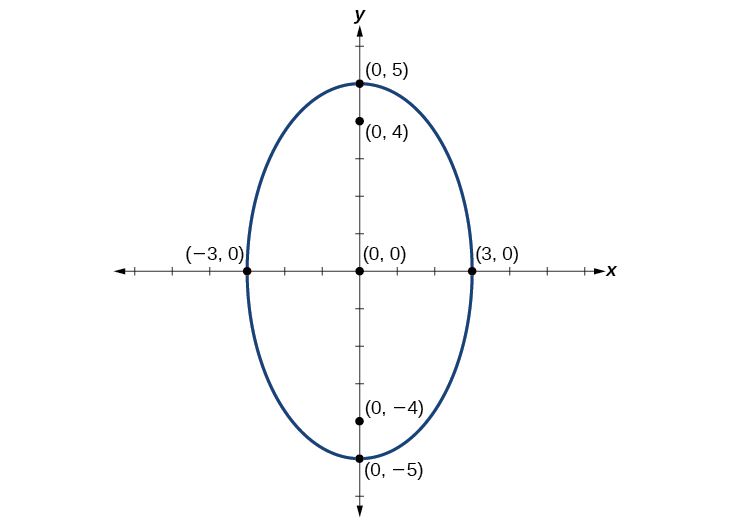
Figura\(\PageIndex{8}\)
Faça um gráfico da elipse dada pela equação\(\dfrac{x^2}{36}+\dfrac{y^2}{4}=1\). Identifique e rotule o centro, os vértices, os co-vértices e os focos.
- Resposta
-
centro:\((0,0)\); vértices:\((\pm 6,0)\); co-vértices:\((0,\pm 2)\); focos:\((\pm 4\sqrt{2},0)\)
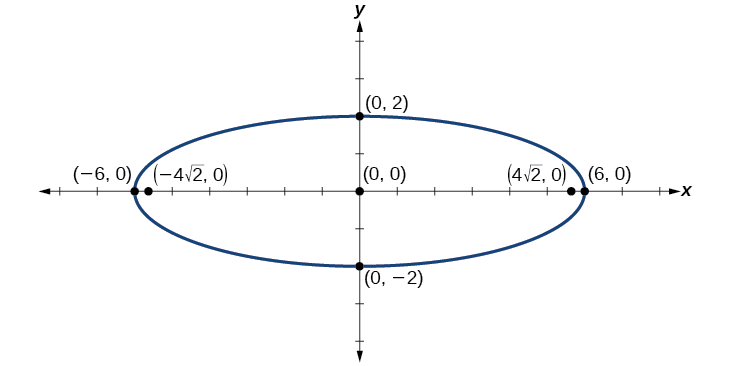
Figura\(\PageIndex{9}\)
Faça um gráfico da elipse dada pela equação\(4x^2+25y^2=100\). Reescreva a equação na forma padrão. Em seguida, identifique e rotule o centro, os vértices, os co-vértices e os focos.
Solução
Primeiro, use álgebra para reescrever a equação na forma padrão.
\[\begin{align} 4x^2+25y^2&=100 \nonumber \\ \dfrac{4x^2}{100}+\dfrac{25y^2}{100}&=\dfrac{100}{100} \nonumber \\ \dfrac{x^2}{25}+\dfrac{y^2}{4}&=1 \nonumber \end{align} \nonumber \]
Em seguida, determinamos a posição do eixo principal. Porque\(25>4\), o eixo principal está no\(x\) eixo -. Portanto, a equação está na forma\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), onde\(a^2=25\)\(b^2=4\) e. Daqui resulta que:
- o centro da elipse é\((0,0)\)
- as coordenadas dos vértices são\((\pm a,0)=(\pm \sqrt{25},0)=(\pm 5,0)\)
- as coordenadas dos co-vértices são\((0,\pm b)=(0,\pm \sqrt{4})=(0,\pm 2)\)
- as coordenadas dos focos são\((\pm c,0)\), onde\(c^2=a^2−b^2\). Resolvendo para\(c\), temos:
\[\begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\ &=\pm \sqrt{25−4} \nonumber \\ &=\pm \sqrt{21} \nonumber \end{align} \nonumber \]
Portanto, as coordenadas dos focos são\((\pm \sqrt{21},0)\).
Em seguida, traçamos e rotulamos o centro, os vértices, os co-vértices e os focos e desenhamos uma curva suave para formar a elipse.
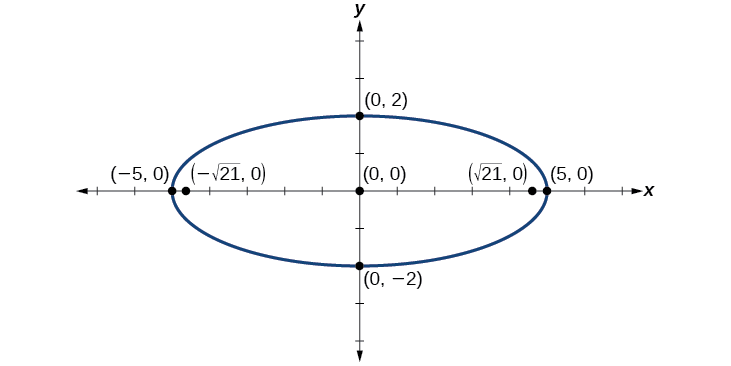
Figura\(\PageIndex{10}\)
Faça um gráfico da elipse dada pela equação\(49x^2+16y^2=784\). Reescreva a equação na forma padrão. Em seguida, identifique e rotule o centro, os vértices, os co-vértices e os focos.
- Resposta
-
Forma padrão:\(\dfrac{x^2}{16}+\dfrac{y^2}{49}=1\); centro:\((0,0)\); vértices:\((0,\pm 7)\); co-vértices:\((\pm 4,0)\); focos:\((0,\pm \sqrt{33})\)
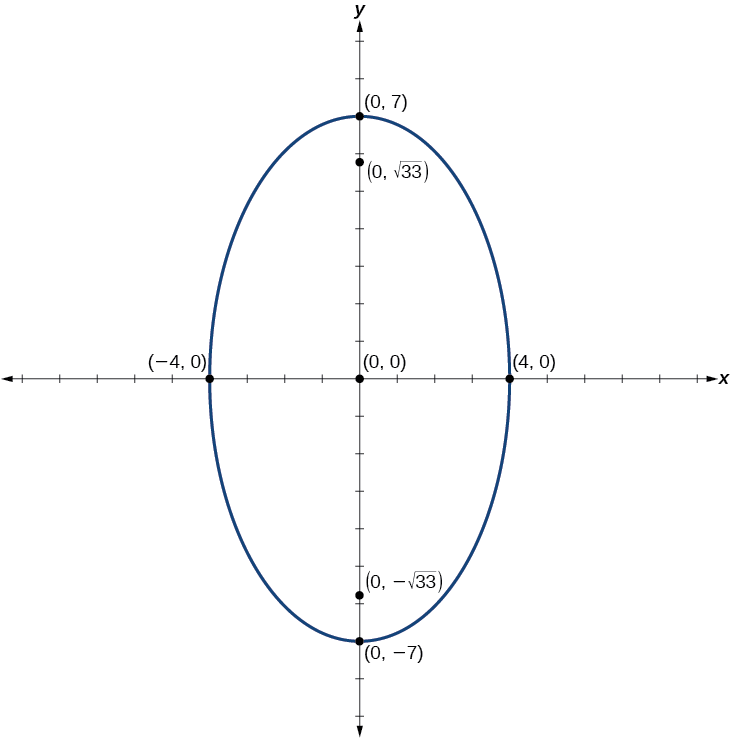
Figura\(\PageIndex{11}\)
Representação gráfica de elipses não centradas na origem
Quando uma elipse não está centralizada na origem, ainda podemos usar as formas padrão para encontrar as principais características do gráfico. Quando a elipse está centralizada em algum ponto\((h,k)\), usamos as formas padrão\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\),\(a>b\) para elipses horizontais e\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\),\(a>b\) para elipses verticais. A partir dessas equações padrão, podemos determinar facilmente o centro, vértices, co-vértices, focos e posições dos eixos maior e menor.
- Use as formas padrão das equações de uma elipse para determinar o centro, a posição do eixo maior, vértices, co-vértices e focos.
- Se a equação estiver na forma\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\), onde\(a>b\), então
- o centro é\((h,k)\)
- o eixo principal é paralelo ao\(x\) eixo -
- as coordenadas dos vértices são\((h\pm a,k)\)
- as coordenadas dos co-vértices são\((h,k\pm b)\)
- as coordenadas dos focos são\((h\pm c,k)\)
- Se a equação estiver na forma\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\), onde\(a>b\), então
- o centro é\((h,k)\)
- o eixo principal é paralelo ao\(y\) eixo -
- as coordenadas dos vértices são\((h,k\pm a)\)
- as coordenadas dos co-vértices são\((h\pm b,k)\)
- as coordenadas dos focos são\((h,k\pm c)\)
- Se a equação estiver na forma\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\), onde\(a>b\), então
- Resolva o\(c\) uso da equação\(c^2=a^2−b^2\).
- Faça um gráfico do centro, vértices, co-vértices e focos no plano coordenado e desenhe uma curva suave para formar a elipse.
Faça um gráfico da elipse dada pela equação,\(\dfrac{{(x+2)}^2}{4}+\dfrac{{(y−5)}^2}{9}=1\). Identifique e rotule o centro, os vértices, os co-vértices e os focos.
Solução
Primeiro, determinamos a posição do eixo principal. Porque\(9>4\), o eixo principal é paralelo ao\(y\) eixo -. Portanto, a equação está na forma\(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\), onde\(b^2=4\)\(a^2=9\) e. Daqui resulta que:
- o centro da elipse é\((h,k)=(−2,5)\)
- as coordenadas dos vértices são\((h,k\pm a)=(−2,5\pm \sqrt{9})=(−2,5\pm 3)\), ou\((−2,2)\) e\((−2,8)\)
- as coordenadas dos co-vértices são\((h\pm b,k)=(−2\pm \sqrt{4},5)=(−2\pm 2,5)\), ou\((−4,5)\) e\((0,5)\)
- as coordenadas dos focos são\((h,k\pm c)\), onde\(c^2=a^2−b^2\). Resolvendo para\(c\), temos:
\[ \begin{align} c&=\pm \sqrt{a^2−b^2} \nonumber \\[4pt] &=\pm \sqrt{9−4} \nonumber \\[4pt] &=\pm \sqrt{5} \nonumber \end{align} \nonumber\]
Portanto, as coordenadas dos focos são\((−2,5−\sqrt{5})\)\((−2,5+\sqrt{5})\) e.
Em seguida, traçamos e rotulamos o centro, os vértices, os co-vértices e os focos e desenhamos uma curva suave para formar a elipse.
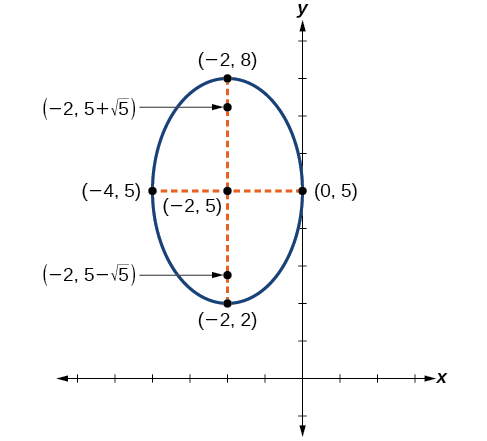
Figura\(\PageIndex{12}\)
Faça um gráfico da elipse dada pela equação\(\dfrac{{(x−4)}^2}{36}+\dfrac{{(y−2)}^2}{20}=1\). Identifique e rotule o centro, os vértices, os co-vértices e os focos.
- Resposta
-
Centro:\((4,2)\); vértices:\((−2,2)\) e\((10,2)\); co-vértices:\((4,2−2\sqrt{5})\) e\((4,2+2\sqrt{5})\); focos:\((0,2)\) e\((8,2)\)
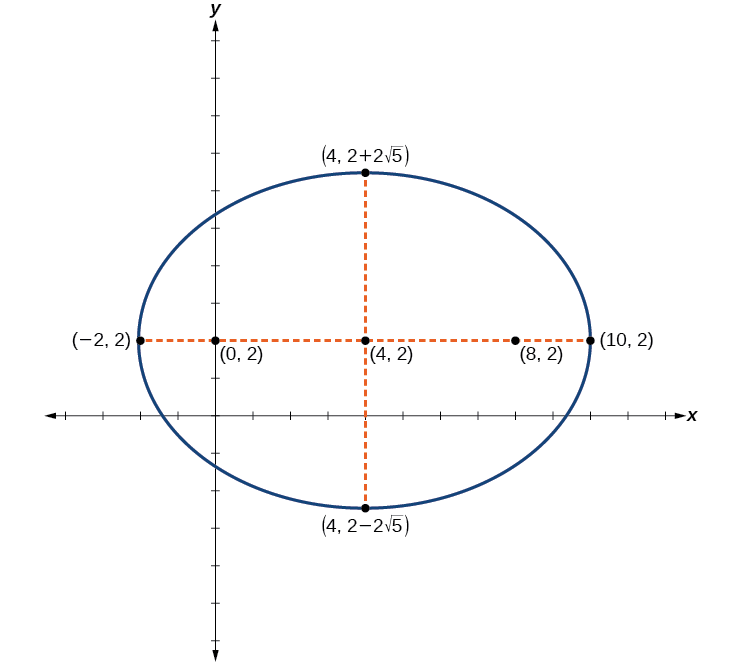
Figura\(\PageIndex{13}\)
- Reconheça que uma elipse descrita por uma equação no formulário\(ax^2+by^2+cx+dy+e=0\) está na forma geral.
- Reorganize a equação agrupando termos que contêm a mesma variável. Mova o termo constante para o lado oposto da equação.
- Considere os coeficientes dos\(y^2\) termos\(x^2\) e na preparação para completar o quadrado.
- Complete o quadrado de cada variável para reescrever a equação na forma da soma dos múltiplos de dois binômios ao quadrado definido igual a uma constante\(m_1{(x−h)}^2+m_2{(y−k)}^2=m_3\),\(m_1\), onde\(m_2\), e\(m_3\) são constantes.
- Divida os dois lados da equação pelo termo constante para expressar a equação na forma padrão.
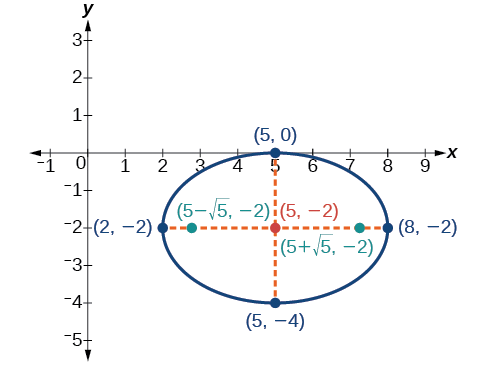
Faça um gráfico da elipse dada pela equação\(4x^2+9y^2−40x+36y+100=0\). Identifique e rotule o centro, os vértices, os co-vértices e os focos.
Solução
Devemos começar reescrevendo a equação na forma padrão.
\(4x^2+9y^2−40x+36y+100=0\)
Agrupe termos que contêm a mesma variável e mova a constante para o lado oposto da equação.
\((4x^2−40x)+(9y^2+36y)=−100\)
Fatize os coeficientes dos termos quadrados.
\(4(x^2−10x)+9(y^2+4y)=−100\)
Complete o quadrado duas vezes. Lembre-se de equilibrar a equação adicionando as mesmas constantes em cada lado.
\(4(x^2−10x+25)+9(y^2+4y+4)=−100+100+36\)
Reescreva como quadrados perfeitos.
\(4{(x−5)}^2+9{(y+2)}^2=36\)
Divida os dois lados pelo termo constante para colocar a equação na forma padrão.
\(\dfrac{{(x−5)}^2}{9}+\dfrac{{(y+2)}^2}{4}=1\)
Agora que a equação está na forma padrão, podemos determinar a posição do eixo principal. Porque\(9>4\), o eixo principal é paralelo ao\(x\) eixo -. Portanto, a equação está na forma\(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\), onde\(a^2=9\)\(b^2=4\) e. Daqui resulta que:
- o centro da elipse é\((h,k)=(5,−2)\)
- as coordenadas dos vértices são\((h\pm a,k)=(5\pm \sqrt{9},−2)=(5\pm 3,−2)\), ou\((2,−2)\) e\((8,−2)\)
- as coordenadas dos co-vértices são\((h,k\pm b)=(5,−2\pm \sqrt{4})=(5,−2\pm 2)\), ou\((5,−4)\) e\((5,0)\)
- as coordenadas dos focos são\((h\pm c,k)\), onde\(c^2=a^2−b^2\). Resolvendo para\(c\), temos:
\[\begin{align*} c&=\pm \sqrt{a^2-b^2}\\ &=\pm \sqrt{9-4}\\ &=\pm \sqrt{5} \end{align*}\]
Portanto, as coordenadas dos focos são\((5−\sqrt{5},−2)\)\((5+\sqrt{5},−2)\) e.
Em seguida, traçamos e rotulamos o centro, os vértices, os co-vértices e os focos e desenhamos uma curva suave para formar a elipse, conforme mostrado na Figura\(\PageIndex{14}\).

Figura\(\PageIndex{14}\)
Expresse a equação da elipse dada na forma padrão. Identifique o centro, os vértices, os co-vértices e os focos da elipse.
\(4x^2+y^2−24x+2y+21=0\)
- Resposta
-
\(\dfrac{{(x−3)}^2}{4}+\dfrac{{(y+1)}^2}{16}=1\); centro:\((3,−1)\); vértices:\((3,−5)\) e\((3,3)\); co-vértices:\((1,−1)\) e\((5,−1)\); focos:\((3,−1−2\sqrt{3})\) e\((3,−1+2\sqrt{3})\)
Resolvendo problemas aplicados envolvendo elipses
Muitas situações do mundo real podem ser representadas por elipses, incluindo órbitas de planetas, satélites, luas e cometas, e formas de quilhas de barcos, lemes e algumas asas de avião. Um dispositivo médico chamado litotriptor usa refletores elípticos para quebrar cálculos renais gerando ondas sonoras. Alguns edifícios, chamados de câmaras sussurrantes, são projetados com cúpulas elípticas para que uma pessoa sussurrando em um foco possa ser facilmente ouvida por alguém parado no outro foco. Isso ocorre devido às propriedades acústicas de uma elipse. Quando uma onda sonora se origina em um foco de uma câmara sussurrante, a onda sonora é refletida pela cúpula elíptica e volta para o outro foco (Figura\(\PageIndex{15}\)). Na câmara de sussurros do Museu da Ciência e Indústria de Chicago, duas pessoas em pé no foco - a cerca de um\(43\) metro de distância - podem ouvir uma à outra sussurrar.
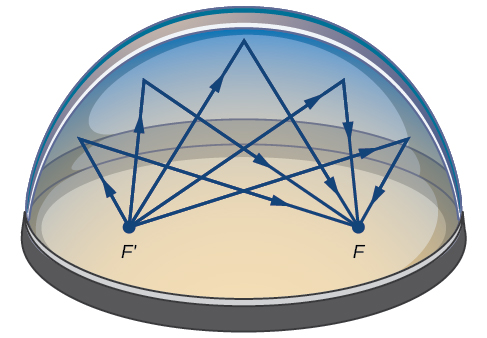
Figura\(\PageIndex{15}\): As ondas sonoras são refletidas entre os focos em uma sala elíptica, chamada de câmara sussurrante.
O Salão Estatuário no Edifício do Capitólio em Washington, D.C. é uma câmara sussurrante. Suas dimensões são\(46\) pés de largura por\(96\) pés de comprimento, conforme mostrado na Figura\(\PageIndex{16}\).
- Qual é a forma padrão da equação da elipse que representa o contorno da sala? Dica: assuma uma elipse horizontal e deixe o centro da sala ser o ponto\((0,0)\).
- Se dois senadores que estão nos focos desta sala puderem ouvir um ao outro sussurrar, a que distância estão os senadores? Arredonde até o pé mais próximo.
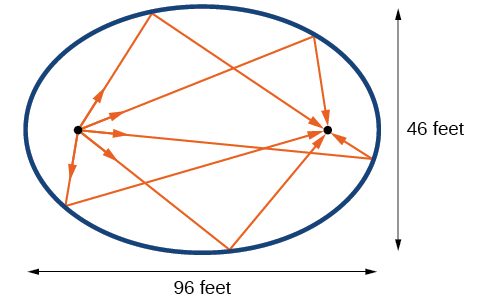
Figura\(\PageIndex{16}\)
Solução
- Estamos assumindo uma elipse horizontal com centro\((0,0)\), então precisamos encontrar uma equação da forma\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), onde\(a>b\). Sabemos que o comprimento do eixo maior,\(2a\), é maior que o comprimento do eixo menor,\(2b\). Portanto, o comprimento da sala, 96, é representado pelo eixo principal, e a largura da sala, 46, é representada pelo eixo menor.
Portanto, a equação da elipse é\ [(dfrac {x^2} {2304} +\ dfrac {y^2} {529} =1\)
- Resolvendo para\(a\), temos\(2a=96\), então\(a=48\),\(a^2=2304\) e.
- Resolvendo para\(b\), temos\(2b=46\), então\(b=23\),\(b^2=529\) e.
- Para encontrar a distância entre os senadores, devemos encontrar a distância entre os focos,\((\pm c,0)\), onde\(c^2=a^2−b^2\). Resolvendo para\(c\), temos:
\[\begin{align*} c^2&=a^2-b^2\\ c^2&=2304-529\qquad \text{Substitute using the values found in part } (a)\\ c&=\pm \sqrt{2304-529}\qquad \text{Take the square root of both sides.}\\ c&=\pm \sqrt{1775}\qquad \text{Subtract.}\\ c&\approx \pm 42\qquad \text{Round to the nearest foot.} \end{align*}\]
Os pontos\((\pm 42,0)\) representam os focos. Assim, a distância entre os senadores é de\(2(42)=84\) pés.
Suponha que uma câmara sussurrante tenha\(480\) pés de comprimento e\(320\) pés de largura.
- Qual é a forma padrão da equação da elipse que representa a sala? Dica: assuma uma elipse horizontal e deixe o centro da sala ser o ponto\((0,0)\).
- Se duas pessoas estão nos focos desta sala e podem ouvir uma à outra sussurrar, a que distância estão as pessoas? Arredonde até o pé mais próximo.
- Responda a um
-
\(\dfrac{x^2}{57,600}+\dfrac{y^2}{25,600}=1\)
- Resposta b
-
As pessoas estão a poucos\(358\) metros de distância.
Acesse esses recursos on-line para obter instruções adicionais e praticar com elipses.
Equações-chave
| Elipse horizontal, centro na origem | \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\),\(a>b\) |
| Elipse vertical, centro na origem | \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\),\(a>b\) |
| Elipse horizontal, centro\((h,k)\) | \(\dfrac{{(x−h)}^2}{a^2}+\dfrac{{(y−k)}^2}{b^2}=1\),\(a>b\) |
| Elipse vertical, centro\((h,k)\) | \(\dfrac{{(x−h)}^2}{b^2}+\dfrac{{(y−k)}^2}{a^2}=1\),\(a>b\) |
Conceitos-chave
- Uma elipse é o conjunto de todos os pontos\((x,y)\) em um plano de forma que a soma de suas distâncias de dois pontos fixos seja uma constante. Cada ponto fixo é chamado de foco (plural: focos).
- Quando dadas as coordenadas dos focos e vértices de uma elipse, podemos escrever a equação da elipse na forma padrão. Veja o exemplo\(\PageIndex{1}\) e o exemplo\(\PageIndex{2}\).
- Quando é dada uma equação para uma elipse centrada na origem na forma padrão, podemos identificar seus vértices, co-vértices, focos e os comprimentos e posições dos eixos maior e menor para representar graficamente a elipse. Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- Quando dada a equação de uma elipse centrada em algum ponto diferente da origem, podemos identificar suas principais características e representar graficamente a elipse. Veja o exemplo\(\PageIndex{5}\) e o exemplo\(\PageIndex{6}\).
- Situações do mundo real podem ser modeladas usando as equações padrão das elipses e depois avaliadas para encontrar as principais características, como comprimentos de eixos e distância entre focos. Veja o exemplo\(\PageIndex{7}\).


