6.E: Funções periódicas (exercícios)
- Page ID
- 189171
6.1: Gráficos das funções seno e cosseno
No capítulo sobre Funções trigonométricas, examinamos funções trigonométricas, como a função seno. Nesta seção, vamos interpretar e criar gráficos de funções de seno e cosseno
Verbal
1) Por que as funções seno e cosseno são chamadas de funções periódicas?
- Resposta
-
As funções seno e cosseno têm a propriedade de,\(f(x+P)=f(x)\) por um certo tempo\(P\). Isso significa que os valores da função se repetem para cada\(P\) unidade no\(x\) eixo y.
2) Como o gráfico de se\(y=\sin x\) compara com o gráfico de\(y=\cos x\)? Explique como você pode traduzir horizontalmente o gráfico de\(y=\sin x\) para obter\(y=\cos x\).
3) Para a equação\(A \cos(Bx+C)+D\)
- Resposta
-
O valor absoluto da constante\(A\) (amplitude) aumenta o intervalo total e a constante\(D\) (deslocamento vertical) desloca o gráfico verticalmente.
4) Como o intervalo de uma função senoidal traduzida se relaciona com a equação\(y=A \sin(Bx+C)+D\)
5) Como o círculo unitário pode ser usado para construir o gráfico de\(f(t)=\sin t\)?
- Resposta
-
No ponto em que o lado terminal de\(t\) cruza o círculo unitário, você pode determinar se\(\sin t\) é igual à\(y\) coordenada -do ponto.
Gráfica
Para os exercícios a seguir, faça um gráfico de dois períodos completos de cada função e indique a amplitude, o período e a linha média. Indique os\(y\) valores máximo e mínimo e seus\(x\) valores -correspondentes em um período para\(x>0\). Arredonde as respostas para duas casas decimais, se necessário.
6)\(f(x)=2\sin x\)
7)\(f(x)=\dfrac{2}{3}\cos x\)
- Resposta
-
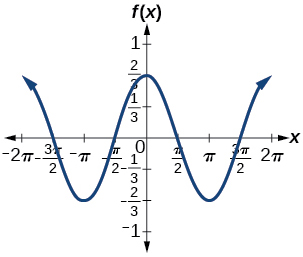
amplitude:\(\dfrac{2}{3}\)
; ; ; ; ;
8)\(f(x)=-3\sin x\)
9)\(f(x)=4\sin x\)
- Resposta
-
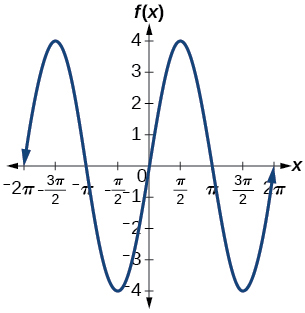
amplitude:\(4\); período:\(2\pi \)
; ; ; ;
10)\(f(x)=2\cos x\)
11)\(f(x)=\cos (2x)\)
- Resposta
-
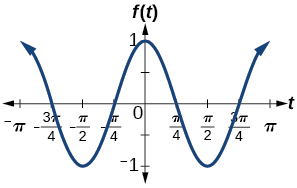
amplitude:\(1\); período:\(\pi\)
; ; ; ;
12)\(f(x)=2 \sin \left(\dfrac{1}{2}x\right)\)
13)\(f(x)=4 \cos(\pi x)\)
- Resposta
-
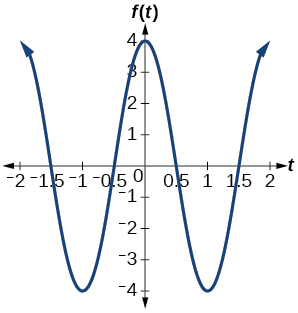
amplitude:\(4\); período:\(2\); linha média:\(y=0\)
; ;
14)\(f(x)=3 \cos\left(\dfrac{6}{5}x\right)\)
15)\(y=3 \sin(8(x+4))+5\)
- Resposta
-
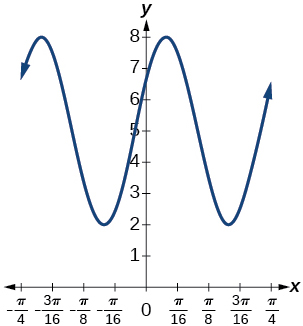
amplitude:\(3\); período:\(\dfrac{\pi}{4}\); linha média:\(y=5\);
máximo:\(y=8\) ocorre em\(x = -4+\frac{21\pi}{16} \approx 0.123\);
mínimo:\(y=2\) ocorre em\(x = -4+\frac{23\pi}{16} \approx 0.516\); deslocamento
horizontal:\(-4\); translação vertical\(5\);
um período ocorre de\(x=-4+\frac{22\pi}{16} \approx 0.320\) a\(x=-4+\frac{26\pi}{16} \approx 1.105 \)
16)\(y=2 \sin(3x-21)+4\)
17)\(y=5 \sin(5x+20)-2\)
- Resposta
-
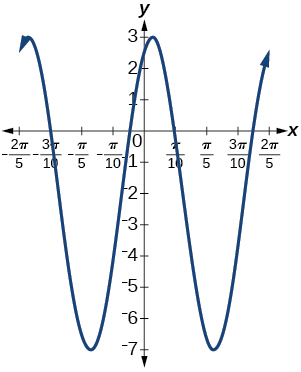
amplitude:\(5\); período:\(\dfrac{2\pi }{5}\); linha média:\(y=-2\);
máximo:\(y=3\) ocorre em\(x= -4+\frac{13\pi}{10} \approx 0.084\);
mínimo:\(y=-7\) ocorre em\(x=-4+\frac{15\pi}{10} \approx 0.712\); mudança de
fase:\(-4\); translação vertical:\(-2\);
um período completo pode ser representado graficamente\(x=-4+\frac{7\pi}{5} \approx 0.398\) em\(x=-4+\frac{9\pi}{5} \approx 1.655 \)
Para os exercícios a seguir, faça um gráfico de um período completo de cada função, começando em\(x=0\).
Para cada função, indique a amplitude, o período e a linha média.
Indique os\(y\) valores máximo e mínimo e seus\(x\) valores -correspondentes em um período para\(x>0\).
Indique a mudança de fase e a translação vertical, se aplicável.
Arredonde as respostas para duas casas decimais, se necessário.
18)\(f(t)=2\sin \left(t-\dfrac{5\pi}{6} \right)\)
19)\(f(t)=-\cos \left(t+\dfrac{\pi}{3} \right)+1\)
- Resposta
-
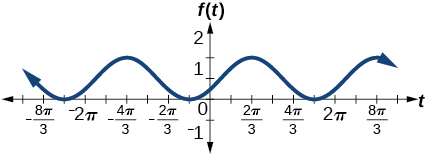
amplitude:\(1\); período:\(2\pi \); linha média:\(y=1\);
máximo:\(y=2\) ocorre em\(t=\frac{2\pi}{3} \approx 2.094\);
mínimo:\(y=0\) ocorre em\(t=\frac{2\pi}{3} \approx5.24\); mudança de
fase:\(-\dfrac{\pi}{3}\); translação vertical:\(1\);
um período completo é de\(t=\frac{2\pi}{3} \approx 2.094\) para\(t=\frac{8\pi}{3} \approx 8.378 \)
20)\(f(t)=4\cos \left(2\left (t+\dfrac{\pi}{4} \right ) \right)-3\)
21)\(f(t)=-\sin \left (\dfrac{1}{2}t+\dfrac{5\pi}{3} \right )\)
- Resposta
-
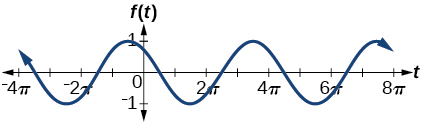amplitude:\(1\); período:\(4\pi\); linha média:\(y=0\);
máximo:\(y=1\) ocorre em\(t=\frac{11\pi}{3} \approx 11.52\);
mínimo:\(y=-1\) ocorre em\(t=\frac{5\pi}{3} \approx 5.24\); mudança de
fase:\(-\dfrac{10\pi}{3}\); mudança vertical:\(0\);
um período completo é de \(t=\frac{2\pi}{3} \approx 2.094\)para\(t=\frac{14\pi}{3} \approx 14.661 \)
22)\(f(x)=4\sin \left (\dfrac{\pi}{2}(x-3) \right )+7\)
23) Determine a amplitude, a linha média, o período e uma equação envolvendo a função seno para o gráfico mostrado na Figura abaixo.
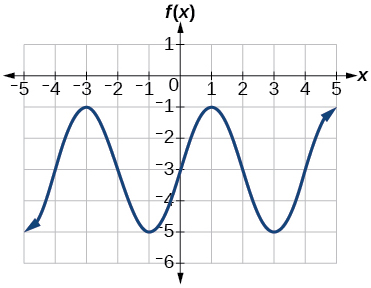
- Resposta
-
23. amplitude:\(2\); linha média:\(y=-3\) período:\(4\); equação:\(f(x)=2\sin \left (\dfrac{\pi}{2}x \right )-3\)
24) Determine a amplitude, a linha média, o período e uma equação envolvendo a função cosseno para o gráfico mostrado na Figura abaixo.
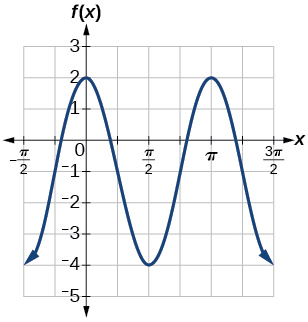
25) Determine a amplitude, a linha média, o período e uma equação envolvendo a função cosseno para o gráfico mostrado na Figura abaixo.
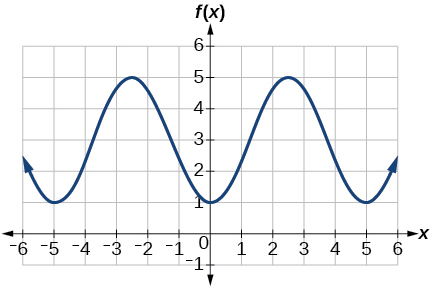
- Resposta
-
25. amplitude:\(2\); período:\(5\); linha média:\(y=3\) equação:\(f(x)=-2\cos \left (\dfrac{2\pi}{5}x \right )+3\)
26) Determine a amplitude, a linha média, o período e uma equação envolvendo a função seno para o gráfico mostrado na Figura abaixo.
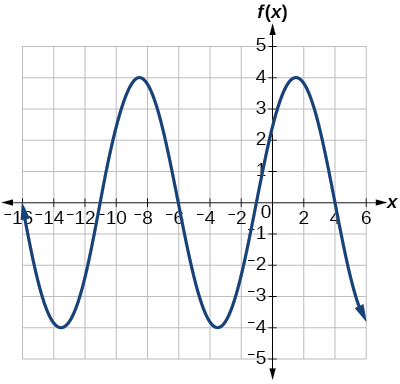
27) Determine a amplitude, a linha média, o período e uma equação envolvendo a função cosseno para o gráfico mostrado na Figura abaixo.
- Resposta
-
27. amplitude:\(4\); período:\(2\); linha média:\(y=0\); equação:\(f(x)=-4\cos \left (\pi \left (x-\dfrac{\pi}{2} \right ) \right )\)
28) Determine a amplitude, a linha média, o período e uma equação envolvendo a função seno para o gráfico mostrado na Figura abaixo.
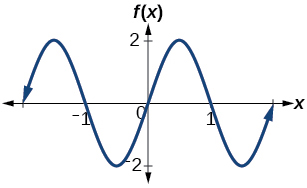
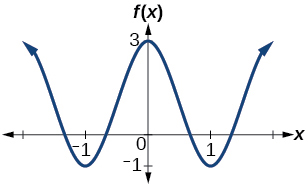
29) Determine a amplitude, a linha média, o período e uma equação envolvendo a função cosseno para o gráfico mostrado na Figura abaixo.
- Resposta
-
29. amplitude:\(2\); período:\(2\);\(y=1\) equação da linha média:\(f(x)=2\cos \left (\pi x \right )+1\)
30) Determine a amplitude, a linha média, o período e uma equação envolvendo a função seno para o gráfico mostrado na Figura abaixo.
Algébrico
Para os exercícios a seguir, deixe\(f(x)=\sin x \)
31) Ativado\([0,2\pi )\)
32) Ativado\([0,2\pi )\), resolva\(f(x)=\dfrac{1}{2}\).
- Resposta
-
\(\dfrac{\pi }{6}\),\(\dfrac{5\pi }{6}\)
33) Avalie\(f \left( \dfrac{\pi }{2} \right) \)
34) Em\([0,2\pi)\),\(f(x)=\dfrac{\sqrt{2}}{2}\). Encontre todos os valores de\(x\).
- Resposta
-
\(\dfrac{\pi }{4}\),\(\dfrac{3\pi }{4}\)
35) Ativado\([0,2\pi )\)
36) Ativado\([0,2\pi )\)
- Resposta
-
\(\dfrac{3\pi }{2}\)
37) Mostre que\(f(-x) = -f(x)\)
Para os exercícios a seguir, deixe\(f(x)=\cos x\)
38) Ativado\([0,2\pi )\)
- Resposta
-
\(\dfrac{\pi }{2}\),\(\dfrac{3\pi }{2}\)
39) Ativado\([0,2\pi )\)
40) Ativado\([0,2\pi )\)
- Resposta
-
\(\dfrac{\pi }{2}\),\(\dfrac{3\pi }{2}\)
41) Ativado\([0,2\pi )\)
42) Ativado\([0,2\pi )\)
- Resposta
-
\(\dfrac{\pi }{6}\),\(\dfrac{11\pi }{6}\)
Tecnologia
43) Gráfico\(h(x)=x+\sin x\) sobre\([0,2\pi ]\)
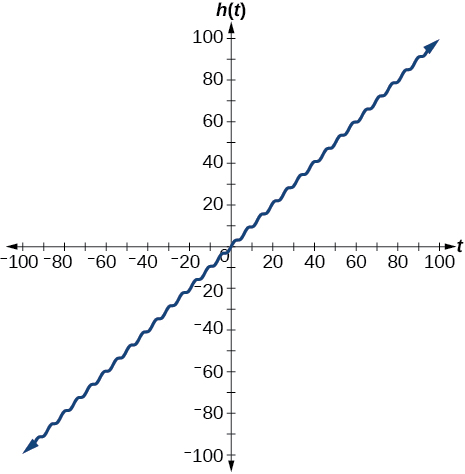
44) Gráfico\(h(x)=x+\sin x\) sobre\([-100,100]\)
- Resposta
-
O gráfico parece linear. As funções lineares dominam a forma do gráfico para grandes valores de\(x\).
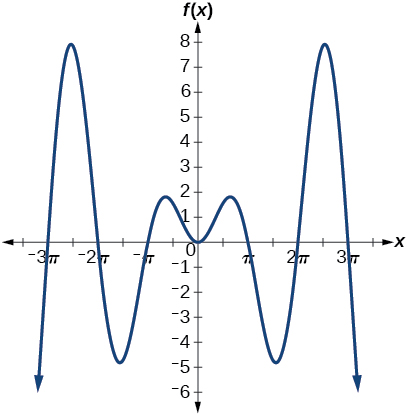
45) Faça um gráfico\(f(x)=x\sin x\)\([0,2\pi ]\) e verbalize como o gráfico varia do gráfico de\(f(x)=x\sin x\).
46) Faça um gráfico\(f(x)=x\sin x\) na janela\([-10,10]\) e explique o que o gráfico mostra.
- Resposta
-
O gráfico é simétrico em relação ao\(y\) eixo -e não há amplitude porque a função não é periódica.
47) Faça um gráfico\(f(x)=\dfrac{\sin x}{x}\) na janela\([-5\pi , 5\pi ]\) e explique o que o gráfico mostra.
Aplicativos do mundo real
48) Uma roda gigante tem\(25\) metros de diâmetro e é embarcada em uma plataforma que está\(1\) metros acima do solo. A posição das seis horas na roda gigante está nivelada com a plataforma de carregamento. A roda\(1\) completa a rotação em\(10\) minutos. A função\(h(t)\) fornece a altura de uma pessoa em metros acima do solo,\(t\) minutos após o volante começar a girar
- Encontre a amplitude, a linha média e o período de\(h(t)\).
- Encontre uma fórmula para a função de altura\(h(t)\).
- A que altura está uma pessoa depois de\(5\) alguns minutos?
- Resposta
-
- Amplitude:\(12.5\); período:\(10\); linha média:\(y=13.5\)
- \(h(t)=12.5\sin\left ( \dfrac{\pi}{5}(t-2.5) \right )+13.5\)
- \(26\)pés
6.2: Gráficos das outras funções trigonométricas
Esta seção aborda a representação gráfica das curvas Tangente, Cossecante, Secante e Cotangente.
Verbal
1) Explique como o gráfico da função seno pode ser usado para representar graficamente\(y=\csc x\).
Resposta
Uma vez que\(y=\csc x\) é a função recíproca de\(y=\sin x\)
2) Como o gráfico de pode\(y=\cos x\) ser usado para construir o gráfico de\(y=\sec x\)?
3) Explique por que o período de\(y=\tan x\) é igual\(\pi \) a.
Resposta
As respostas podem variar. Usando o círculo unitário, pode-se mostrar isso\(y=\tan (x+\pi )=\tan x\).
4) Por que não há interceptações no gráfico de\(y=\csc x\)?
5) Como o período de se\(y=\csc x\) compara com o período de\(y=\sin x\)?
Resposta
-
O período é o mesmo:\(2\pi \)
Algébrico
Para os exercícios 6-9, combine cada função trigonométrica com um dos gráficos a seguir.
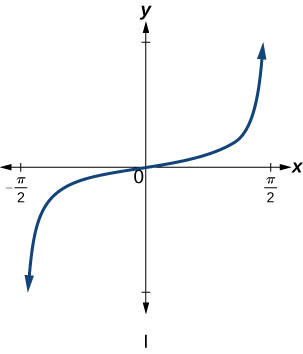
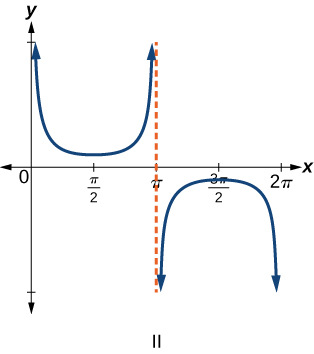
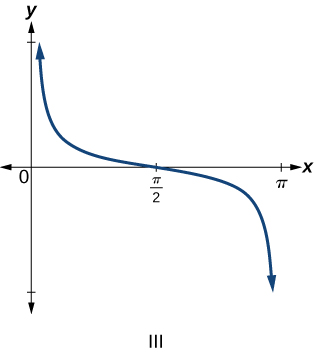
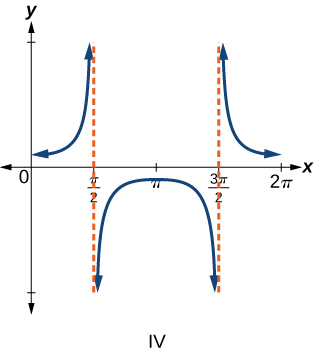
6)\(f(x)=\tan x\)
7)\(f(x)=\sec x\)
- Resposta
-
\(\mathrm{IV}\)
8)\(f(x)=\csc x\)
9)\(f(x)=\cot x\)
- Resposta
-
\(\mathrm{III}\)
Para os exercícios 10-16, encontre o período e o deslocamento horizontal de cada uma das funções.
10)\(f(x)=2\tan(4x-32)\)
11)\(h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)\)
- Resposta
-
período:\(8\); deslocamento horizontal:\(1\) unidade para a esquerda
12)\(m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)\)
13) Se\(\tan x=-1.5\)
- Resposta
-
\(1.5\)
14) Se\(\sec x=2\), encontre\(\sec (-x)\).
15) Se\(\csc x=-5\), encontre\(\csc (-x)\).
- Resposta
-
\(5\)
16) Se\(x\sin x=2\), encontre\((-x)\sin (-x)\).
Para os exercícios 17-18, reescreva cada expressão para que o argumento\(x\) seja positivo.
17)\(\cot(-x)\cos(-x)+\sin(-x)\)
- Resposta
-
\(-\cot x \cos x-\sin x\)
18)\(\cos(-x)+\tan(-x)\sin(-x)\)
Gráfica
Para os exercícios 19-36, esboce dois períodos do gráfico para cada uma das seguintes funções. Identifique o fator de alongamento, o período e as assíntotas.
19)\(f(x)=2\tan(4x-32)\)
- Resposta
-
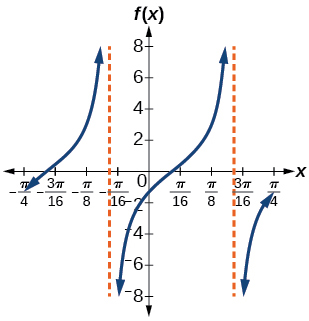
fator de alongamento:\(2\); período:\(\dfrac{\pi }{3}\)
;
20)\(h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)\)
21)\(m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)\)
- Resposta
-
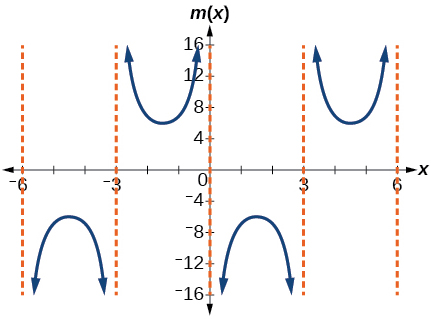
fator de alongamento:\(6\); período:\(6\); assíntotas:\(x=k\), onde\(k\) é um número inteiro
22)\(j(x)=\tan \left ( \dfrac{\pi }{2}x \right )\)
23)\(p(x)=\tan \left ( x-\dfrac{\pi }{2} \right )\)
- Resposta
-
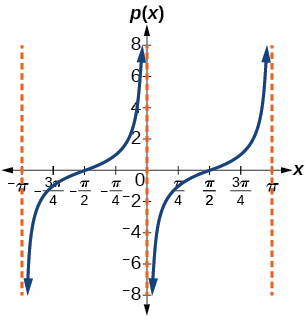
fator de alongamento:\(1\); período:\(\pi \)
;
24)\(f(x)=4\tan (x)\)
25)\(f(x)=\tan \left ( x+\dfrac{\pi }{4} \right )\)
- Resposta
-
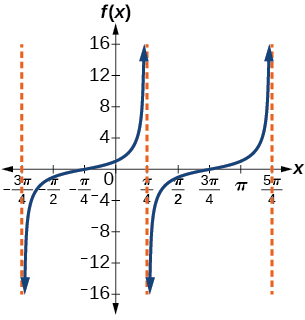
Fator de alongamento:\(1\); período:\(\pi \)
;
26)\(f(x)=\pi \tan(\pi x- \pi)-\pi\)
27)\(f(x)=2\csc (x)\)
- Resposta
-
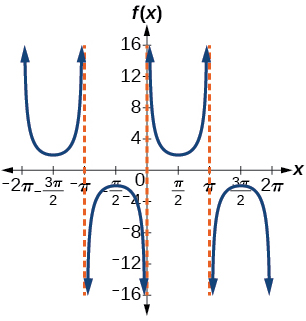
fator de alongamento:\(2\); período:\(2\pi \)
;
28)\(f(x)=-\dfrac{1}{4}\csc(x)\)
29)\(f(x)=4\sec(3x)\)
- Resposta
-
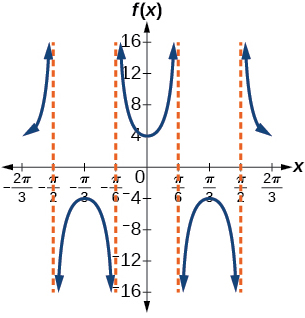
fator de alongamento:\(4\); período:\(\dfrac{2\pi }{3}\)
;
30)\(f(x)=-3\cot(2x)\)
31)\(f(x)=7\sec(5x)\)
- Resposta
-
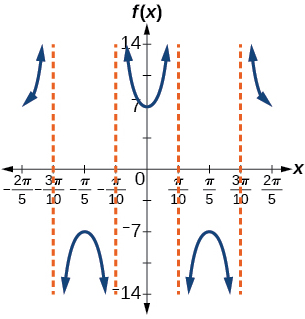
fator de alongamento:\(7\); período:\(\dfrac{2\pi }{5}\)
;
32)\(f(x)=\dfrac{9}{10}\csc(\pi x)\)
33)\(f(x)=2\csc \left(x+\dfrac{\pi }{4} \right)-1\)
- Resposta
-
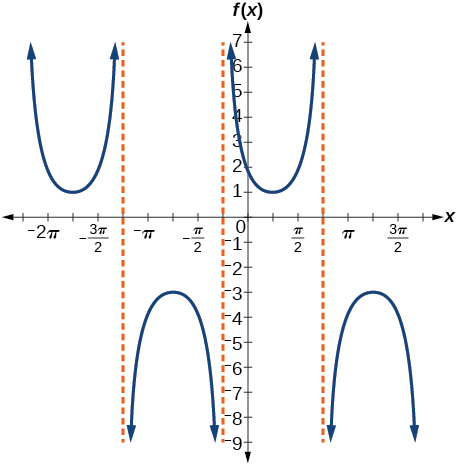
Fator de alongamento:\(2\); período:\(2\pi \); assíntotas:\(x=-\dfrac{\pi}{4}+\pi k\), onde\(k\) é um número inteiro
34)\(f(x)=-\sec \left(x-\dfrac{\pi }{3} \right)-2\)
35)\(f(x)=\dfrac{7}{5}\csc \left(x-\dfrac{\pi }{4} \right)\)
- Resposta
-
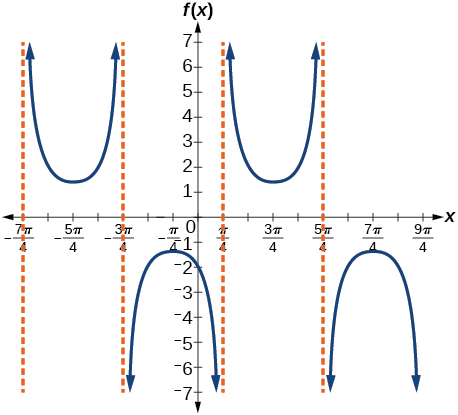
Fator de alongamento:\(\dfrac{7}{5}\); período:\(2\pi \); assíntotas:\(x=\dfrac{\pi}{4}+\pi k\), onde\(k\) é um número inteiro
36)\(f(x)=5\left (\cot \left(x+\dfrac{\pi }{2} \right) -3 \right )\)
37) Uma curva tangente,\(A=1\)
- Resposta
-
\(y=\tan\left(3\left(x-\dfrac{\pi}{4} \right) \right)+2\)
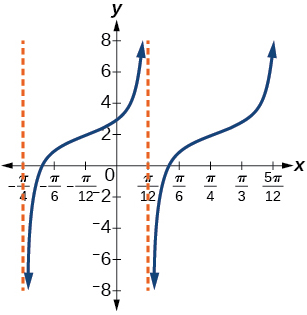
38) Uma curva tangente\(A=-2\), período de\(\dfrac{\pi }{4}\); e mudança de fase\((h, k)=\left (- \dfrac{\pi }{4},-2 \right )\)
Para os exercícios 39-45, encontre uma equação para o gráfico de cada função.
39)
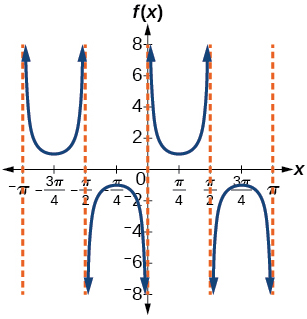
- Resposta
-
\(f(x)=\csc (2x)\)
40)
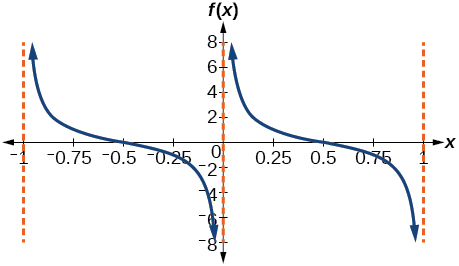
41)
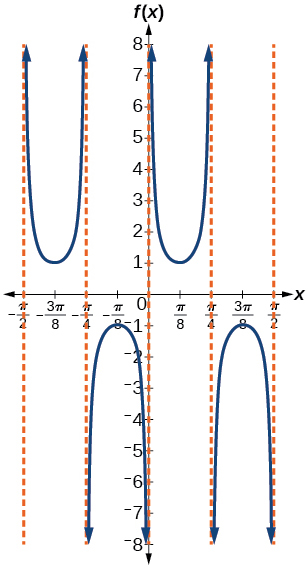
- Resposta
-
\(f(x)=\csc (4x)\)
42)
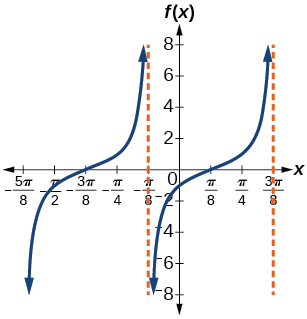
43)
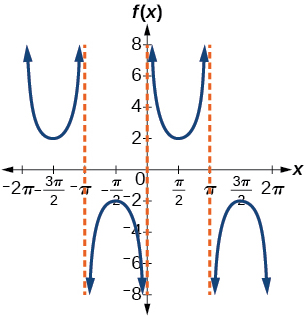
- Resposta
-
\(f(x)=2\csc x\)
44)
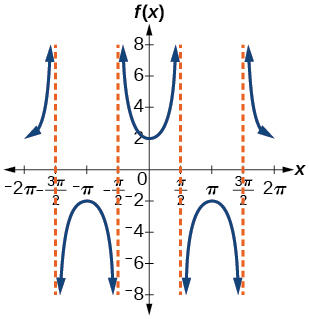
45)
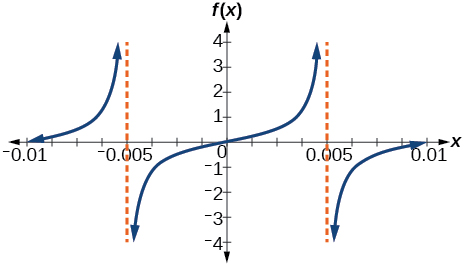
- Resposta
-
\(f(x)=\dfrac{1}{2}\tan (100\pi x)\)
Tecnologia
Para os exercícios 46-53, use uma calculadora gráfica para representar graficamente dois períodos da função dada. Nota: a maioria das calculadoras gráficas não tem um botão cossecante; portanto, você precisará inserir\(\csc x\) como\(\dfrac{1}{\sin x}\)
46)\(f(x)=| \csc (x) |\)
47)\(f(x)=| \cot (x) |\)
- Resposta
-
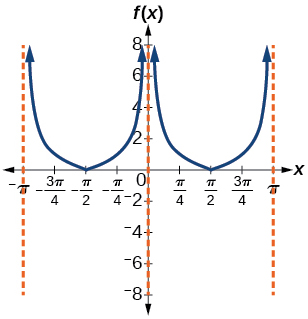
48)\(f(x)=2^{\csc (x)}\)
49)\(f(x)=\frac{\csc (x)}{\sec (x)}\)
- Resposta
-
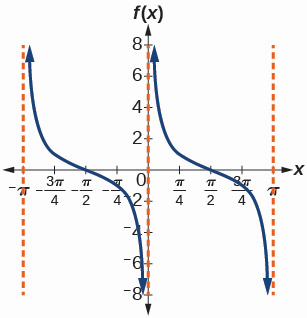
50) Gráfico\(f(x)=1+\sec^2(x)-\tan^2(x)\)
51)\(f(x)=\sec(0.001x)\)
- Resposta
-
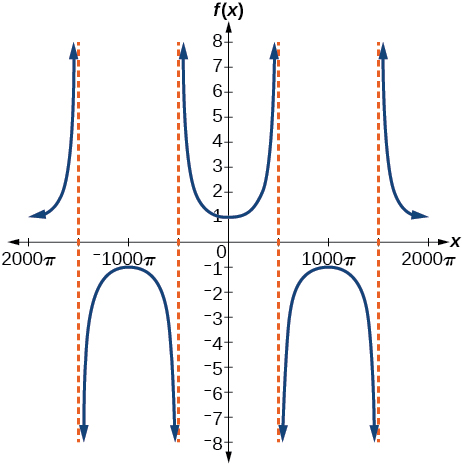
52)\(f(x)=\cot(100 \pi x)\)
53)\(f(x)=\sin^2x +\cos^2x\)
- Resposta
-
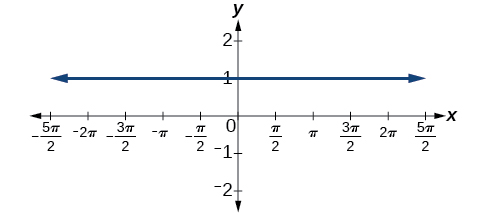
Aplicativos do mundo real
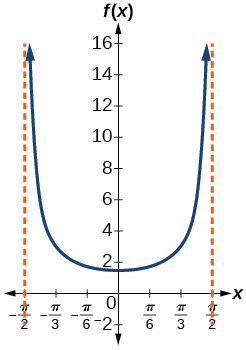
54) A função\(f(x)=20\tan\left(\dfrac{\pi }{10}x\right)\) marca a distância no movimento de um feixe de luz de um carro da polícia através de uma parede por tempo\(x\)
- Gráfico sobre o intervalo\([0,5]\)
- Encontre e interprete o fator de alongamento, o período e a assíntota.
- Avalie\(f(10)\)\(f(2.5)\) e discuta os valores da função nessas entradas.
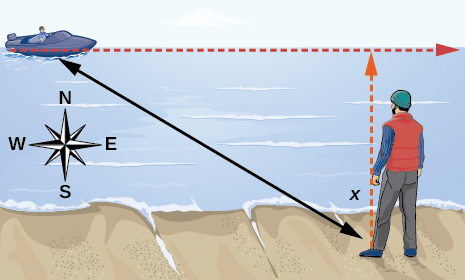
55) De pé na margem de um lago, um pescador vê um barco muito distante à sua esquerda. Deixe\(x\)
- Para que serve um domínio razoável\(d(x)\)?
- Gráfico\(d(x)\) sobre este domínio.
- Encontre e discuta o significado de qualquer assíntota vertical no gráfico de\(d(x)\).
- Calcular e interpretar\(d\left ( -\dfrac{\pi }{3} \right )\)
. - Calcular e interpretar\(d\left ( \dfrac{\pi }{6} \right )\)
. - Qual é a distância mínima entre o pescador e o barco? Quando isso ocorre?
- Resposta
-
- \(\left ( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right )\)
- \(x=-\dfrac{\pi }{2}\)e\(x=\dfrac{\pi }{2}\)
; - \(3\); quando\(x=-\dfrac{\pi }{3}\)
, - \(1.73\); quando\(x=\dfrac{\pi }{6}\)
, - \(1.5\)km; quando\(x=0\)
56) Um telêmetro a laser está bloqueado em um cometa que se aproxima da Terra. A distância\(g(x)\)
- Gráfico\(g(x)\) do intervalo\([0,35]\).
- Avalie\(g(5)\) e interprete as informações.
- Qual é a distância mínima entre o cometa e a Terra? Quando isso ocorre? A qual constante na equação isso corresponde?
- Encontre e discuta o significado de qualquer assíntota vertical.
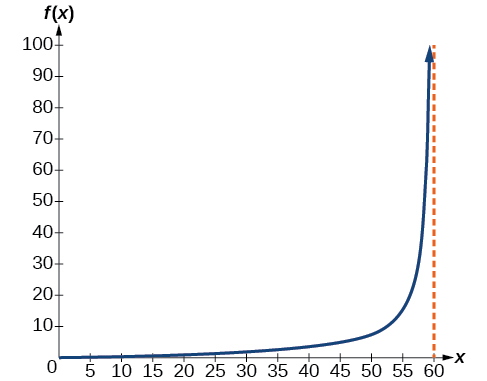
57) Uma câmera de vídeo é focada em um foguete em uma plataforma de lançamento a\(2\) quilômetros da câmera. O ângulo de elevação do solo até o foguete após\(x\) segundos é\(\dfrac{\pi }{120}x\).
- Escreva uma função expressando a altitude\(h(x)\)
, - Gráfico\(h(x)\) do intervalo\((0,60)\).
- Avalie e interprete os valores\(h(0)\)\(h(30)\) e.
- O que acontece com os valores de\(h(x)\) quando\(x\) se aproxima dos\(60\) segundos? Interprete o significado disso em termos do problema.
- Resposta
-
- \(h(x)=2\tan \left(\dfrac{\pi }{120}x \right)\)
- \(h(0)=0\)
: : - À medida que\(x\) se aproxima dos\(60\) segundos, os valores de\(h(x)\) crescem cada vez mais. A distância até o foguete está crescendo tanto que a câmera não consegue mais rastreá-lo.
6.3: Funções trigonométricas inversas
Nesta seção, exploraremos as funções trigonométricas inversas. As funções trigonométricas inversas “desfazem” o que a função trigonométrica original “faz”, como é o caso de qualquer outra função e seu inverso. Em outras palavras, o domínio da função inversa é o intervalo da função original e vice-versa.
Verbal
1) Por que as funções\(f(x)=\sin^{-1}x\) e\(g(x)=\cos^{-1}x\) têm intervalos diferentes?
- Resposta
-
A função\(y=\sin x\) é individual ativada\(\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]\)
; ;
2) Como as funções\(y=\cos x\) e\(y=\cos^{-1}x\) são funções inversas, por que é\(\cos^{-1}\left (\cos \left (-\dfrac{\pi }{6} \right ) \right )\)
3) Explique o significado de\(\dfrac{\pi }{6}=\arcsin (0.5)\).
- Resposta
-
\(\dfrac{\pi }{6}\)é a medida radiana de um ângulo entre\(-\dfrac{\pi }{2}\) e\(\dfrac{\pi }{2}\) cujo seno é\(0.5\).
4) A maioria das calculadoras não tem uma chave para avaliar\(\sec ^{-1}(2)\)
5) Por que o domínio do seno deve funcionar,\(\sin x\)
- Resposta
-
Para que qualquer função tenha um inverso, a função deve ser individual e passar no teste da linha horizontal. A função seno regular não é individual, a menos que seu domínio seja restrito de alguma forma. Os matemáticos concordaram em restringir a função seno ao intervalo para\(\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]\) que ela seja um a um e possua um inverso.
6) Discuta por que essa afirmação está incorreta:\(\arccos(\cos x)=x\) para todos\(x\).
7) Determine se a seguinte afirmação é verdadeira ou falsa e explique sua resposta:\(\arccos(-x)=\pi - \arccos x\)
- Resposta
-
É verdade. O ângulo,\(\theta _1\) que é igual a\(\arccos(-x)\),\(x>0\), será um ângulo do segundo quadrante com ângulo de referência,\(\theta _2\), onde\(\theta _2\) é igual a\(\arccos x\),\(x>0\). Uma vez que\(\theta _2\) é o ângulo de referência para\(\theta _1\),\(\theta _2=\pi - \theta _1\) e\(\arccos(-x)=\pi - \arccos x-\)
Algébrico
Para os exercícios 8-16, avalie as expressões.
8)\(\sin^{-1}\left(\dfrac{\sqrt{2}}{2}\right)\)
9)\(\sin^{-1}\left(-\dfrac{1}{2}\right)\)
- Resposta
-
\(-\dfrac{\pi }{6}\)
10)\(\cos^{-1}\left(-\dfrac{1}{2}\right)\)
11)\(\cos^{-1}\left(-\dfrac{\sqrt{2}}{2}\right)\)
- Resposta
-
\(\dfrac{3\pi }{4}\)
12)\(\tan^{-1}(1)\)
13)\(\tan^{-1}(-\sqrt{3})\)
- Resposta
-
\(-\dfrac{\pi }{3}\)
14)\(\tan^{-1}(-1)\)
15)\(\tan^{-1}(\sqrt{3})\)
- Resposta
-
\(\dfrac{\pi }{3}\)
16)\(\tan^{-1}\left(\dfrac{-1}{\sqrt{3}}\right)\)
Para os exercícios 17-21, use uma calculadora para avaliar cada expressão. Expresse as respostas até o centésimo mais próximo.
17)\(\cos^{-1}(-0.4)\)
- Resposta
-
\(1.98\)
18)\(\arcsin (0.23)\)
19)\(\arccos \left(\dfrac{3}{5}\right)\)
- Resposta
-
\(0.93\)
20)\(\cos^{-1}(-0.8)\)
21)\(\tan^{-1}(6)\)
- Resposta
-
\(1.41\)
Para os exercícios 22-23, encontre o ângulo\(\theta\) no triângulo reto fornecido. Arredonde as respostas para o centésimo mais próximo.
22)
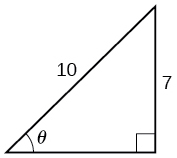
23)
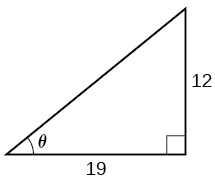
- Resposta
-
\(0.56\)radianos
Para os exercícios 24-36, encontre o valor exato, se possível, sem uma calculadora. Se isso não for possível, explique o porquê.
24)\(\sin^{-1}(\cos(\pi))\)
25)\(\tan^{-1}(\sin(\pi))\)
- Resposta
-
\(0\)
26)\(\cos^{-1}\left(\sin \left(\dfrac{\pi}{3} \right)\right)\)
27)\(\tan^{-1}\left(\sin \left(\dfrac{\pi}{3} \right)\right)\)
- Resposta
-
\(0.71\)
28)\(\sin^{-1}\left(\cos \left(\dfrac{-\pi}{2} \right)\right)\)
29)\(\tan^{-1}\left(\sin \left(\dfrac{4\pi}{3} \right)\right)\)
- Resposta
-
\(-0.71\)
30)\(\sin^{-1}\left(\sin \left(\dfrac{5\pi}{6} \right)\right)\)
31)\(\tan^{-1}\left(\sin \left(\dfrac{-5\pi}{2} \right)\right)\)
- Resposta
-
\(-\dfrac{\pi}{4}\)
32)\(\cos \left(\sin^{-1} \left(\dfrac{4}{5} \right)\right)\)
33)\(\sin \left(\cos^{-1} \left(\dfrac{3}{5} \right)\right)\)
- Resposta
-
\(0.8\)
34)\(\sin \left(\tan^{-1} \left(\dfrac{4}{3} \right)\right)\)
35)\(\cos \left(\tan^{-1} \left(\dfrac{12}{5} \right)\right)\)
- Resposta
-
\(\dfrac{5}{13}\)
36)\(\cos \left(\sin^{-1} \left(\dfrac{1}{2} \right)\right)\)
Para os exercícios 37-41, determine o valor exato da expressão em termos de\(x\) com a ajuda de um triângulo de referência.
37)\(\tan \left(\sin^{-1} (x-1)\right)\)
- Resposta
-
\(\dfrac{x-1}{\sqrt{-x^2+2x}}\)
38)\(\sin \left(\sin^{-1} (1-x)\right)\)
39)\(\cos \left(\sin^{-1} \left(\dfrac{1}{x}\right)\right)\)
- Resposta
-
\(\dfrac{\sqrt{x^2-1}}{x}\)
40)\(\cos \left(\tan^{-1} (3x-1)\right)\)
41)\(\tan \left(\sin^{-1} \left(x+\dfrac{1}{2}\right)\right)\)
- Resposta
-
\(\dfrac{x+0.5}{\sqrt{-x^2-x+\tfrac{3}{4}}}\)
Extensões
Para o exercício 42, avalie a expressão sem usar uma calculadora. Forneça o valor exato.
2)\(\dfrac{\sin^{-1}\left ( \tfrac{1}{2} \right )-\cos^{-1}\left ( \tfrac{\sqrt{2}}{2} \right )+\sin^{-1}\left ( \tfrac{\sqrt{3}}{2} \right )-\cos^{-1}(1)}{\cos^{-1}\left ( \tfrac{\sqrt{3}}{2} \right )-\sin^{-1}\left ( \tfrac{\sqrt{2}}{2} \right )+\cos^{-1}\left ( \tfrac{1}{2} \right )-\sin^{-1}(0)}\)
Para os exercícios 43-47, encontre a função se \(\sin t = \dfrac{x}{x+1}\)
43)\(\cos t\)
- Resposta
-
\(\dfrac{\sqrt{2x+1}}{x+1}\)
44)\(\sec t\)
45)\(\cot t\)
- Resposta
-
\(\dfrac{\sqrt{2x+1}}{x}\)
(46)\(\cos \left(\sin^{-1} \left(\dfrac{x}{x+1}\right)\right)\)
47)\(\tan^{-1} \left(\dfrac{x}{\sqrt{2x+1}}\right)\)
- Resposta
-
\(t\)
Gráfica
48) Representar graficamente\(y=\sin^{-1} x\) e indicar o domínio e o alcance da função.
49) Gráfico\(y=\arccos x\)
- Resposta
-
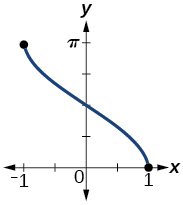
domínio\([-1,1]\)
;
50) Faça um gráfico de um ciclo\(y=\tan^{-1} x\) e indique o domínio e o alcance da função.
51) Por que valor de\(x\) faz\(\sin x=\sin^{-1} x\)? Use uma calculadora gráfica para aproximar a resposta.
- Resposta
-
aproximadamente\(x=0.00\)
52) Por que valor de\(x\) faz\(\cos x=\cos^{-1} x\)? Use uma calculadora gráfica para aproximar a resposta.
Aplicativos do mundo real
53) Suponha que uma escada de um\(13\) pé esteja encostada em um prédio, chegando ao fundo de uma janela do segundo andar,\(12\) pés acima do solo. Qual ângulo, em radianos, a escada faz com o prédio?
Resposta
-
\(0.395\)radianos
54) Suponha que você dirija\(0.6\) milhas em uma estrada para que a distância vertical mude de\(0\) para\(150\) pés. Qual é o ângulo de elevação da estrada?
55) Um triângulo isósceles tem dois lados congruentes de\(9\) polegadas de comprimento. O lado restante tem um comprimento de\(8\) polegadas. Encontre o ângulo que um lado de\(9\) polegadas faz com o lado de\(8\) -polegada.
- Resposta
-
\(1.11\)radianos
56) Sem usar uma calculadora, aproxime o valor de\(\arctan (10,000)\)
57) Uma treliça para o telhado de uma casa é construída a partir de dois triângulos retos idênticos. Cada um tem uma base de\(12\) pés e altura de\(4\) pés. Encontre a medida do ângulo agudo adjacente ao lado do\(4\) pé.
- Resposta
-
\(1.25\)radianos
58) A linha\(y=\dfrac{3}{5}x\) passa pela origem no\(x,y\) plano -. Qual é a medida do ângulo que a linha faz com o\(x\) eixo positivo?
59) A linha\(y=\dfrac{-3}{7}x\) passa pela origem no\(x,y\) plano -. Qual é a medida do ângulo que a linha faz com o\(x\) eixo negativo?
- Resposta
-
\(0.405\)radianos
60) Qual porcentagem de nível uma estrada deve ter se o ângulo de elevação da estrada for de\(4\) graus? (O grau percentual é definido como a mudança na altitude da estrada em uma distância horizontal de\(100\) -pés. Por exemplo, uma\(5\%\) inclinação significa que a estrada sobe\(5\) pés para cada\(100\) metro de distância horizontal.)
61) Uma escada\(20\) de pés se inclina contra a lateral de um prédio, de modo que o pé da escada fique a\(10\) pés da base do prédio. Se as especificações exigirem que o ângulo de elevação da escada esteja entre\(35\) e\(45\) graus, a colocação dessa escada atende às especificações de segurança?
- Resposta
-
Não. O ângulo que a escada faz com a horizontal é de\(60\) graus.
62) Suponha que uma escada de 3\(15\) metros se incline contra a lateral de uma casa de forma que o ângulo de elevação da escada seja de\(42\) graus. A que distância fica o pé da escada do lado da casa?