5.3: As outras funções trigonométricas

Objetivos de

• Encontre os valores exatos das funções trigonométricas secante, cossecante, tangente e cotangente de\(\frac{\pi}{3}\)\(\frac{\pi}{4}\),,\(\frac{\pi}{6}\) e.
• Use ângulos de referência para avaliar as funções trigonométricas secante, tangente e cotangente.
• Use propriedades de funções trigonométricas pares e ímpares.
• Reconheça e use identidades fundamentais.
• Avalie funções trigonométricas com uma calculadora.

Uma rampa para cadeiras de rodas que atenda aos padrões da Lei dos Americanos com Deficiência deve fazer um ângulo com o solo cuja tangente seja\(\frac{1}{12}\) ou menor, independentemente de seu comprimento. Uma tangente representa uma proporção, então isso significa que para cada 1 polegada de subida, a rampa deve ter 12 polegadas de percurso. As funções trigonométricas nos permitem especificar as formas e proporções dos objetos independentemente das dimensões exatas. Já definimos as funções seno e cosseno de um ângulo. Embora seno e cosseno sejam as funções trigonométricas mais usadas, existem outras quatro. Juntos, eles formam o conjunto de seis funções trigonométricas. Nesta seção, investigaremos as funções restantes.

Encontrando valores exatos das funções trigonométricas Secante, Cossecante, Tangente e Cotangente

Para definir as funções restantes, mais uma vez desenharemos um círculo unitário com um ponto\((x,y)\) correspondente a um ângulo de\(t\), conforme mostrado na Figura\(\PageIndex{1}\). Assim como o seno e o cosseno, podemos usar as\((x,y)\) coordenadas para encontrar as outras funções.

Figura\(\PageIndex{1}\)

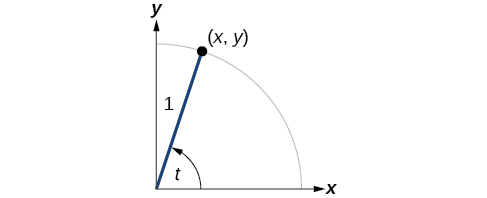
A primeira função que definiremos é a tangente. A tangente de um ângulo é a razão entre o valor y e o valor x do ponto correspondente no círculo unitário. Na Figura\(\PageIndex{1}\), a tangente do ângulo\(t\) é igual\(\frac{y}{x},x≠0 \) a. Como o valor y é igual ao seno de\(t\), e o valor x é igual ao cosseno de\(t\), a tangente do ângulo também\(t\) pode ser definida como\( \frac{ \sin t}{ \cos t}, \cos t≠0.\) A função tangente é abreviada como\( \tan.\) As três funções restantes podem ser expressas como recíprocos de funções que já definimos.

• A função secante é a recíproca da função cosseno. Na Figura\(\PageIndex{1}\), a secante do ângulo\(t\) é igual\(\frac{1}{ \cos t} = \frac{1}{x},x≠0\) a. A função secante é abreviada como\( \sec \).
• A função cotangente é a recíproca da função tangente. Na Figura\(\PageIndex{1}\), a cotangente do ângulo\(t\) é igual a\( \frac{ \cos t}{ \sin t}= \frac{x}{y}, y≠0.\) A função cotangente é abreviada como\( \cot.\)
• A função cossecante é a recíproca da função senoidal. Na Figura\(\PageIndex{1}\), a cossecante do ângulo\(t\) é igual a\(\frac{1}{ \sin t}= \frac{1}{y},y≠0.\) A função cossecante é abreviada como\( \csc.\)

FUNÇÕES TANGENTE, SECANTE, COSECANTE E COTANGENTE

Se\(t\) for um número real e\((x,y)\) for um ponto em que o lado terminal de um ângulo de\(t\) radianos intercepta o círculo unitário, então

\[\begin{align} \tan t &= \frac{y}{x},x≠0 \\ \sec t & =\frac{1}{x},x≠0 \\ \csc t &=\frac{1}{y},y≠0 \\ \cot t &= \frac{x}{y},y≠0 \end{align}\]

Exemplo\(\PageIndex{1}\): Finding Trigonometric Functions from a Point on the Unit Circle

O ponto\((−\frac{\sqrt{3}}{2},\frac{1}{2})\) está no círculo unitário, conforme mostrado na Figura\(\PageIndex{2}\). Encontre\( \sin t, \cos t, \tan t, \sec t, \csc t,\)\( \cot t\) e.

Figura\(\PageIndex{2}\)

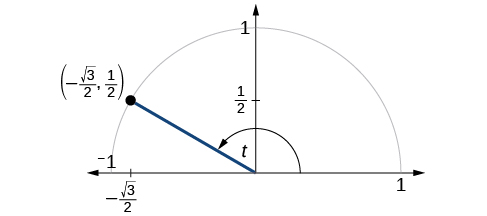
Solução

Como sabemos as\((x,y)\) coordenadas do ponto no círculo unitário indicado pelo ângulo\(t\), podemos usar essas coordenadas para encontrar as seis funções:

\[\begin{align*} \sin t &=y=\dfrac{1}{2} \\ \cos t &=x= −\dfrac{\sqrt{3}}{2} \\ \tan t &= \dfrac{y}{x}= \dfrac{\frac{1}{2}}{−\frac{\sqrt{3}}{2}}=\dfrac{1}{2}(−\dfrac{2}{\sqrt{3}})=−\dfrac{1}{\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \\ \sec t &= \dfrac{1}{x}=\dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2}{\sqrt{3}}=−\dfrac{2\sqrt{3}}{3} \\ \csc t &= \dfrac{1}{y}=\dfrac{1}{\frac{1}{2}}=2 \\ \cot t &= \dfrac{x}{y}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\dfrac{\sqrt{3}}{2}(\dfrac{2}{1})=−\sqrt{3} \end{align*}\]

Exercício\(\PageIndex{1}\):

O ponto\((\frac{\sqrt{2}}{2},−\frac{\sqrt{2}}{2})\) está no círculo unitário, conforme mostrado na Figura\(\PageIndex{3}\). Encontre\( \sin t, \cos t, \tan t, \sec t, \csc t,\)\( \cot t\) e.

Figura\(\PageIndex{3}\)

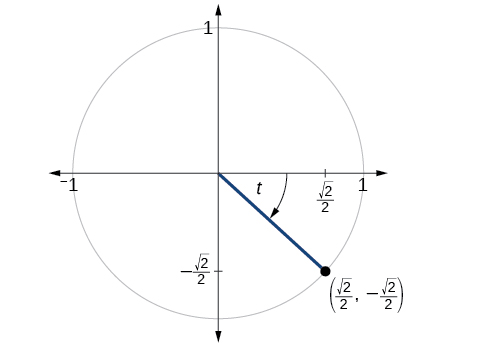
Solução

\( \sin t=−\frac{\sqrt{2}}{2}, \cos t= \frac{\sqrt{2}}{2}, \tan t=−1, \sec t=\sqrt{2}, \csc t=−\sqrt{2}, \cot t=−1\)

Exemplo\(\PageIndex{2}\): Finding the Trigonometric Functions of an Angle

Encontre\( \sin t, \cos t, \tan t, \sec t, \csc t, \) e\( \cot t\) quando\(t=\frac{π}{6}\).

Solução

Anteriormente, usamos as propriedades dos triângulos equiláteros para demonstrar isso\( \sin \frac{π}{6}=\frac{1}{2}\)\( \cos \frac{π}{6}=\frac{\sqrt{3}}{2} \) e. Podemos usar esses valores e as definições de tangente, secante, cossecante e cotangente como funções de seno e cosseno para encontrar os valores restantes da função.

\[ \begin{align*} \tan \dfrac{π}{6} & = \dfrac{ \sin \frac{π}{6}}{\cos \frac{π}{6}} \\ & = \dfrac{\frac{1}{2} }{\frac{\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \\ \sec \dfrac{π}{6} &= \dfrac{1}{ \cos \frac{π}{6}} \\ & = \dfrac{1}{\frac{\sqrt{3}}{2}} = \dfrac{2}{\sqrt{3}}= \dfrac{2\sqrt{3}}{3} \\ \csc \dfrac{π}{6} &= \dfrac{1}{ \sin \frac{π}{6}}= \dfrac{1}{\frac{1}{2}}=2 \\ \cot \dfrac{π}{6} & = \dfrac{ \cos \frac{π}{6}}{ \sin \frac{π}{6}} \\ &= \dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} =\sqrt{3} \end{align*}\]

Exercício\(\PageIndex{2}\):

Encontre\( \sin t, \cos t, \tan t, \sec t, \csc t,\) e\( \cot t\) quando\(t=\frac{π}{3}.\)

Solução

\(\begin{align} \sin \frac{π}{3} & = \frac{\sqrt{3}}{2} \\ \cos \frac{π}{3} &=\frac{1}{2} \\ \tan \frac{π}{3} &= \sqrt{3} \\ \sec \frac{π}{3} &= 2 \\ \csc \frac{π}{3} &= \frac{2\sqrt{3}}{3} \\ \cot \frac{π}{3} &= \frac{\sqrt{3}}{3} \end{align}\)

Como conhecemos os valores de seno e cosseno para os ângulos comuns do primeiro quadrante, também podemos encontrar os outros valores de função para esses ângulos definindo x x igual ao cosseno e y y igual ao seno e depois usando as definições de tangente, secante, cossecante e cotangente. Os resultados são mostrados na Tabela\(\PageIndex{1}\).

Tabela\(\PageIndex{1}\)

Ângulo	\(0\)	\(\frac{π}{6}, \text{ or } 30°\)	\(\frac{π}{4}, \text{ or } 45°\)	\(\frac{π}{3},\text{ or }60°\)	\(\frac{π}{2},\text{ or }90°\)
Cosseno	\ (0\)” style="alinhamento vertical: médio; ">1	\ (\ frac {π} {6},\ text {ou} 30°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {4},\ text {ou} 45°\)” style="vertical-align:middle; ">\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3},\ text {ou} 60°\)” style="vertical-align:middle; ">\(\frac{1}{2}\)	\ (\ frac {π} {2},\ text {ou} 90°\)” style="vertical-align:middle; ">0
Seno	\ (0\)” style="alinhamento vertical: médio; ">0	\ (\ frac {π} {6},\ text {ou} 30°\)” style="vertical-align:middle; ">\(\frac{1}{2}\)	\ (\ frac {π} {4},\ text {ou} 45°\)” style="vertical-align:middle; ">\(\frac{\sqrt{2}}{2}\)	\ (\ frac {π} {3},\ text {ou} 60°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{2}\)	\ (\ frac {π} {2},\ text {ou} 90°\)” style="vertical-align:middle; ">1
Tangente	\ (0\)” style="alinhamento vertical: médio; ">0	\ (\ frac {π} {6},\ text {ou} 30°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {4},\ text {ou} 45°\)” style="vertical-align:middle; ">1	\ (\ frac {π} {3},\ text {ou} 60°\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (\ frac {π} {2},\ text {ou} 90°\)” style="vertical-align:middle; ">Indefinido
Secante	\ (0\)” style="alinhamento vertical: médio; ">1	\ (\ frac {π} {6},\ text {ou} 30°\)” style="vertical-align:middle; ">\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {4},\ text {ou} 45°\)” style="vertical-align:middle; ">\(\sqrt{2}\)	\ (\ frac {π} {3},\ text {ou} 60°\)” style="vertical-align:middle; ">2	\ (\ frac {π} {2},\ text {ou} 90°\)” style="vertical-align:middle; ">Indefinido
Cossecant	\ (0\)” style="vertical-align:middle; ">Indefinido	\ (\ frac {π} {6},\ text {ou} 30°\)” style="vertical-align:middle; ">2	\ (\ frac {π} {4},\ text {ou} 45°\)” style="vertical-align:middle; ">\(\sqrt{2}\)	\ (\ frac {π} {3},\ text {ou} 60°\)” style="vertical-align:middle; ">\(\frac{2\sqrt{3}}{3}\)	\ (\ frac {π} {2},\ text {ou} 90°\)” style="vertical-align:middle; ">1
Cotangente	\ (0\)” style="vertical-align:middle; ">Indefinido	\ (\ frac {π} {6},\ text {ou} 30°\)” style="vertical-align:middle; ">\(\sqrt{3}\)	\ (\ frac {π} {4},\ text {ou} 45°\)” style="vertical-align:middle; ">1	\ (\ frac {π} {3},\ text {ou} 60°\)” style="vertical-align:middle; ">\(\frac{\sqrt{3}}{3}\)	\ (\ frac {π} {2},\ text {ou} 90°\)” style="vertical-align:middle; ">0

Usando ângulos de referência para avaliar tangente, secante, cossecante e cotangente

Podemos avaliar funções trigonométricas de ângulos fora do primeiro quadrante usando ângulos de referência, como já fizemos com as funções seno e cosseno. O procedimento é o mesmo: Encontre o ângulo de referência formado pelo lado terminal do ângulo dado com o eixo horizontal. Os valores da função trigonométrica para o ângulo original serão os mesmos do ângulo de referência, exceto pelo sinal positivo ou negativo, que é determinado pelos valores x e y no quadrante original. A figura\(\PageIndex{4}\) mostra quais funções são positivas em qual quadrante.

Para nos ajudar a lembrar quais das seis funções trigonométricas são positivas em cada quadrante, podemos usar a frase mnemônica “A Smart Trig Class”. Cada uma das quatro palavras da frase corresponde a um dos quatro quadrantes, começando com o quadrante I e girando no sentido anti-horário. No quadrante I, que é “A”, todas as seis funções trigonométricas são positivas. No quadrante II, “S inteligente”, só que nove e sua função recíproca, cossecante, são positivas. No quadrante III, “anel T”, somente a tangente t e sua função recíproca, cotangente, são positivas. Finalmente, no quadrante IV, “classe C”, somente a cosina e sua função recíproca, secante, são positivas.

Figura\(\PageIndex{4}\)

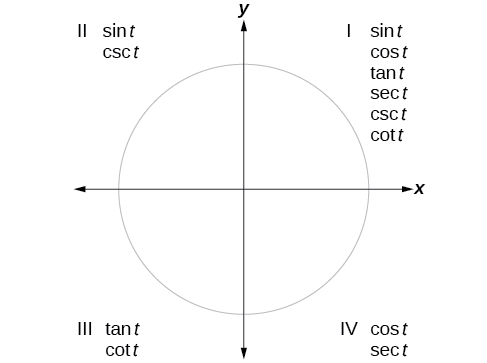
COMO FAZER: Dado um ângulo que não esteja no primeiro quadrante, use ângulos de referência para encontrar todas as seis funções trigonométricas

1. Meça o ângulo formado pelo lado terminal do ângulo dado e pelo eixo horizontal. Esse é o ângulo de referência.
2. Avalie a função no ângulo de referência.
3. Observe o quadrante onde o lado terminal do ângulo original está localizado. Com base no quadrante, determine se a saída é positiva ou negativa.

Exemplo\(\PageIndex{3}\): Using Reference Angles to Find Trigonometric Functions

Use ângulos de referência para encontrar todas as seis funções trigonométricas de\(−\frac{5π}{6}\).

Solução

O ângulo entre o lado terminal desse ângulo e o eixo x é\(\frac{π}{6}\), então esse é o ângulo de referência. Como\(−\frac{5π}{6}\) está no terceiro quadrante, onde ambos\(x\)\(y\) são negativos, cosseno, seno, secante e cossecante serão negativos, enquanto tangente e cotangente serão positivos.

\[ \begin{align} \cos (−\dfrac{5π}{6}) &=−\dfrac{\sqrt{3}}{2}, \sin (−\dfrac{5π}{6})=−\dfrac{1}{2}, \tan (−\dfrac{5π}{6}) = \dfrac{\sqrt{3}}{3} \\ \sec (−\dfrac{5π}{6}) &=−\dfrac{2\sqrt{3}}{3}, \csc (−\dfrac{5π}{6})=−2, \cot (−\dfrac{5π}{6})=\sqrt{3} \end{align} \]

Exercício\(\PageIndex{3}\)

Use ângulos de referência para encontrar todas as seis funções trigonométricas de\(−\frac{7π}{4}\).

Solução

\( \sin (−\frac{7π}{4})= \frac{\sqrt{2}}{2}, \cos(\frac{−7π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{−7π}{4})=1,\)

\( \sec (\frac{−7π}{4})= \sqrt{2}, \csc (\frac{−7π}{4})= \sqrt{2}, \cot (\frac{−7π}{4})=1 \)

Usando funções trigonométricas pares e ímpares

Para podermos usar nossas seis funções trigonométricas livremente com entradas de ângulo positivo e negativo, devemos examinar como cada função trata uma entrada negativa. Ao que parece, há uma diferença importante entre as funções nesse sentido.

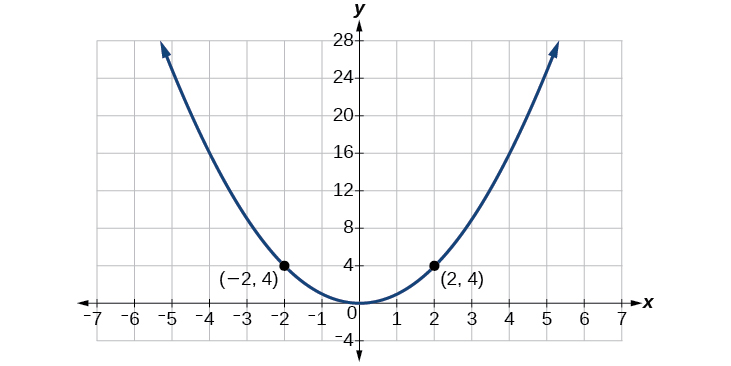
Considere a função\(f(x)=x^2\), mostrada na Figura\(\PageIndex{5}\). O gráfico da função é simétrico em relação ao eixo y. Ao longo da curva, quaisquer dois pontos com valores x opostos têm o mesmo valor de função. Isso corresponde ao resultado do cálculo:\((4)^2=(−4)^2,(−5)^2=(5)^2\) e assim por diante. Então,\(f(x)=x^2\) é uma função par, uma função tal que duas entradas opostas tenham a mesma saída. Isso significa\(f(−x)=f(x)\).

Figura\(\PageIndex{5}\): A função\(f(x)=x^2\) é uniforme.

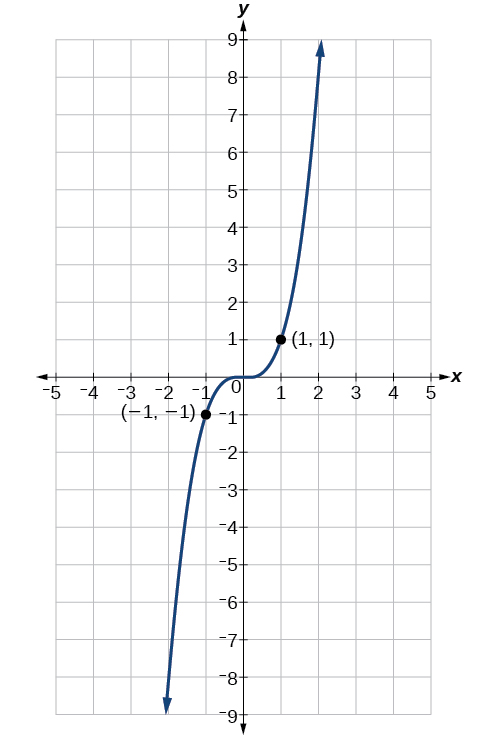
Agora, considere a função\(f(x)=x^3\), mostrada na Figura\(\PageIndex{6}\). O gráfico não é simétrico em relação ao eixo y. Em todo o gráfico, quaisquer dois pontos com valores de x opostos também têm valores de y opostos. Então,\(f(x)=x^3\) é uma função estranha, uma em que duas entradas que são opostas têm saídas que também são opostas. Isso significa\(f(−x)=−f(x)\).

Figura\(\PageIndex{6}\): A função\(f(x)=x^3\) é uma função ímpar.

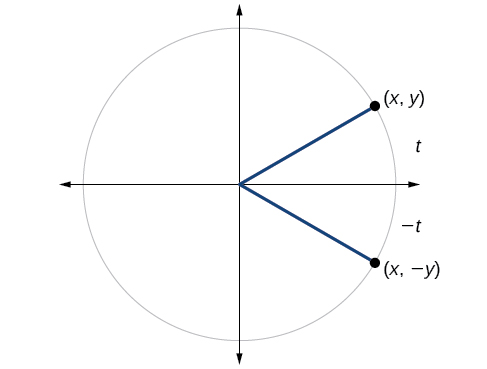
Podemos testar se uma função trigonométrica é par ou ímpar desenhando um círculo unitário com um ângulo positivo e um negativo, como na Figura\(\PageIndex{7}\). O seno do ângulo positivo é\(y\). O seno do ângulo negativo é − y. A função seno, então, é uma função ímpar. Podemos testar cada uma das seis funções trigonométricas dessa forma. Os resultados são mostrados na Tabela\(\PageIndex{2}\).

Figura\(\PageIndex{7}\)

Tabela\(\PageIndex{2}\)

\(\begin{align} \sin t &=y \\ \sin (−t) &=−y \\ \sin t &≠sin(−t) \end{align}\)	\( \begin{align} \cos t &=x \\ \cos (−t)=x \\ \cos t &= \cos (−t) \end{align}\)	\(\begin{align} \tan (t) &= \frac{y}{x} \\ \tan (−t) &=−\frac{y}{x} \\ \tan t &≠ \tan (−t) \end{align}\)
\(\begin{align} \sec t &= \frac{1}{x} \\ \sec (−t) &= \frac{1}{x} \\ \sec t &= \sec (−t) \end{align}\)	\( \begin{align} \csc t &= \frac{1}{y} \\ \csc (−t) &= \frac{1}{−y} \\ \csc t &≠ \csc (−t) \end{align}\)	\( \begin{align} \cot t &= \frac{x}{y} \\ \cot (−t) &= \frac{x}{−y} \\ \cot t & ≠ \cot (−t) \end{align}\)

FUNÇÕES TRIGONOMÉTRICAS PARES E ÍMPARES

• Uma função uniforme é aquela em que\(f(−x)=f(x)\).
• Uma função ímpar é aquela em que\(f(−x)=−f(x)\).

O cosseno e o secante são iguais:

\[ \begin{align} \cos (−t) &= \cos t \\ \sec (−t) &= \sec t \end{align}\]

Seno, tangente, cossecante e cotangente são ímpares:

\[\begin{align} \sin (−t) &=− \sin t \\ \tan (−t) &=−\tan t \\ \csc (−t) &=−\csc t \\ \cot (−t) &=−\cot t \end{align}\]

Exemplo\(\PageIndex{4}\): Using Even and Odd Properties of Trigonometric Functions

Se a secante do ângulo t for 2, qual é a secante de\(−t\)?

Solução

A secante é uma função uniforme. A secante de um ângulo é a mesma que a secante de seu oposto. Então, se a secante do ângulo t é 2, a secante de também\(−t\) é 2.

Exercício\(\PageIndex{4}\):

Se a cotangente do ângulo\(t\) é\(\sqrt{3}\), qual é a cotangente de\(−t?\)

Solução

\(−\sqrt{3}\)

Reconhecer e usar identidades fundamentais

Nós exploramos várias propriedades das funções trigonométricas. Agora, podemos levar os relacionamentos um passo adiante e derivar algumas identidades fundamentais. As identidades são afirmações verdadeiras para todos os valores da entrada na qual estão definidas. Normalmente, as identidades podem ser derivadas de definições e relacionamentos que já conhecemos. Por exemplo, a identidade pitagórica que aprendemos anteriormente foi derivada do Teorema de Pitágoras e das definições de seno e cosseno.

IDENTIDADES FUNDAMENTAIS

Podemos derivar algumas identidades úteis das seis funções trigonométricas. As outras quatro funções trigonométricas podem ser relacionadas às funções seno e cosseno usando essas relações básicas:

\[ \tan t= \dfrac{ \sin t}{ \cos t} \]

\[ \sec t= \dfrac{1}{\cos t}\]

\[ \csc t= \dfrac{1}{\sin t}\]

\[ \cot t= \dfrac{1}{ \tan t}= \dfrac{ \cos t}{ \sin t} \]

Exemplo\(\PageIndex{5}\): Using Identities to Evaluate Trigonometric Functions

1. Dado\( \sin (45°)= \frac{\sqrt{2}}{2}, \cos (45°)= \frac{\sqrt{2}}{2}\), avalie\( \tan(45°).\)
2. Dada\( \sin (\frac{5π}{6})= \frac{1}{2}, \cos( \frac{5π}{6})=−\frac{\sqrt{3}}{2},\) a avaliação\(\sec (\frac{5π}{6})\).

Solução

Como conhecemos os valores de seno e cosseno para esses ângulos, podemos usar identidades para avaliar as outras funções.

1. \[ \begin{align*} \tan(45°) &=\dfrac{ \sin(45°)}{ \cos (45°)} \\ &= \dfrac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} \\ & =1 \end{align*} \]
2. \[\begin{align*} \sec (\dfrac{5π}{6}) &= \dfrac{1}{ \cos (\frac{5π}{6})} \\ &= \dfrac{1}{−\frac{\sqrt{3}}{2}} \\ &= \dfrac{−2\sqrt{3}}{1} \\ &=\dfrac{−2}{\sqrt{3}} \\ &=−\dfrac{2\sqrt{3}}{3} \end{align*}\]

Exercício\(\PageIndex{5}\)

Avalie\(\csc (\frac{7π}{6}).\)

Solução

\(−2\)

Exemplo\(\PageIndex{6}\): Using Identities to Simplify Trigonometric Expressions

Simplifique\(\frac{ \sec t}{ \tan t}.\)

Solução

Podemos simplificar isso reescrevendo as duas funções em termos de seno e cosseno.

\[\begin{array}{lll} \dfrac{\sec t}{\tan t} & =\dfrac{1 / \cos t}{ \sin t / \cos t} & \text{To divide the functions, we multiply by the reciprocal.} \\ \text{} &= \dfrac{1}{\cos t} \dfrac{ \cos t}{\sin t} & \text{Divide out the cosines.} \\ \text{} & =\dfrac{1}{\sin t} & \text{Simplify and use the identity.} \\ \text{} & = \csc t \end{array}\]

Ao mostrar que isso\(\frac{ \sec t}{ \tan t}\) pode ser simplificado para\( \csc t\), de fato, estabelecemos uma nova identidade.

\[ \dfrac{ \sec t}{ \tan t}= \csc t \nonumber \]

Exercício\(\PageIndex{6}\)

Simplifique\(( \tan t)( \cos t).\)

Solução

\( \sin t \)

Formas alternativas da identidade pitagórica

Podemos usar essas identidades fundamentais para derivar formas alternativas da identidade pitagórica,\( \cos ^2 t+ \sin ^2 t=1\). Uma forma é obtida dividindo os dois lados por\( \cos ^2 t:\)

\[ \begin{align} \dfrac{ \cos ^2 t}{ \cos ^2 t} + \dfrac{ \sin ^2 t}{ \cos ^2 t} & = \dfrac{1}{ \cos ^2 t} \\ 1+ \tan ^2 t & = \sec ^2 t \end{align}\]

A outra forma é obtida dividindo os dois lados por\( \sin ^2 t\):

\[ \begin{align} \dfrac{ \cos ^2 t}{ \sin ^2 t}+ \dfrac{ \sin ^2 t}{ \sin ^2 t} &= \dfrac{1}{ \sin ^2 t} \\ \cot ^2 t+1 &= \csc ^2 t \end{align}\]

FORMAS ALTERNATIVAS DA IDENTIDADE PITAGÓRICA

\[1+ \tan ^2 t= \sec ^2 t \]

\[ \cot ^2 t+1= \csc ^2 t\]

Exemplo\(\PageIndex{7}\): Using Identities to Relate Trigonometric Functions

Se cos (t) =1213 cos (t) =1213 e t t estiver no quadrante IV, conforme mostrado na Figura\(\PageIndex{8}\), encontre os valores das outras cinco funções trigonométricas.

Figura\(\PageIndex{8}\)

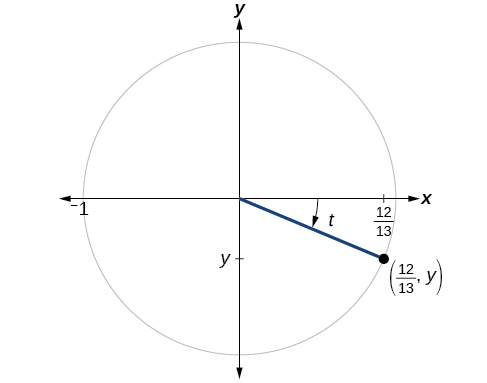
Solução

Podemos encontrar o seno usando a identidade pitagórica,\( \cos ^2 t+ \sin ^2t=1 \), e as funções restantes, relacionando-as com seno e cosseno.

\[ \begin{align} (\dfrac{12}{13})^2+ \sin ^2 t &= 1 \\ \sin ^2 t &=1−(\dfrac{12}{13})^2 \\ \sin ^2 t &=1− \dfrac{144}{169} \\ \sin ^2 t &= \dfrac{25}{169} \\ \sin t &=±\sqrt{\dfrac{25}{169}} \\ \sin t &=±\dfrac{\sqrt{25}}{\sqrt{169}} \\ \sin t &=± \dfrac{5}{13} \end{align} \]

O sinal do seno depende dos valores de y no quadrante em que o ângulo está localizado. Como o ângulo está no quadrante IV, onde os valores de y são negativos, seu seno é negativo,\(−\frac{5}{13}\).

As funções restantes podem ser calculadas usando identidades que as relacionam com seno e cosseno.

\[ \begin{align} \tan t &= \dfrac{\sin t}{ \cos t}=\dfrac{−\frac{5}{13}}{\frac{12}{13}}=−\dfrac{5}{12} \\ \sec t &= \dfrac{1}{ \cos t}=\dfrac{1}{\frac{12}{13}}=\dfrac{13}{12} \\ \csc t &= \dfrac{1}{\sin t}=\dfrac{1}{−\frac{5}{13}} =−\dfrac{13}{5} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{−\frac{5}{12}}=−\dfrac{12}{5} \end{align} \]

Exercício\(\PageIndex{7}\):

Se\( \sec (t)=− \frac{17}{8}\) e\(0<t<π,\) encontre os valores das outras cinco funções.

Solução

\( \cos t=−\frac{8}{17}, \sin t=\frac{15}{17}, \tan t=−\frac{15}{8}\)

\( \csc t= \frac{17}{15}, \cot t=−\frac{8}{15} \)

Conforme discutimos na abertura do capítulo, uma função que repete seus valores em intervalos regulares é conhecida como função periódica. As funções trigonométricas são periódicas. Para as quatro funções trigonométricas, seno, cosseno, cossecante e secante, uma revolução de um círculo\(2π\), ou, resultará nas mesmas saídas para essas funções. E para tangente e cotangente, apenas meia revolução resultará nas mesmas saídas.

Outras funções também podem ser periódicas. Por exemplo, os períodos de meses se repetem a cada quatro anos. Se x x representa o tempo de duração, medido em anos, e\(f(x)\) representa o número de dias em fevereiro, então\(f(x+4)=f(x)\). Esse padrão se repete várias vezes ao longo do tempo. Em outras palavras, a cada quatro anos, é garantido que fevereiro tenha o mesmo número de dias de 4 anos antes. O número positivo 4 é o menor número positivo que satisfaz essa condição e é chamado de período. Um período é o intervalo mais curto no qual uma função completa um ciclo completo. Neste exemplo, o período é 4 e representa o tempo necessário para termos certeza de que fevereiro tem o mesmo número de dias.

PERÍODO DE UMA FUNÇÃO

O período\(P\) de uma função repetida f f é o número que representa o intervalo de forma que\(f(x+P)=f(x)\) para qualquer valor de\(x\).

O período das funções cosseno, seno, secante e cossecante é\(2π\).

O período das funções tangente e cotangente é\(π\).

Exemplo\(\PageIndex{8}\): Finding the Values of Trigonometric Functions

Encontre os valores das seis funções trigonométricas do ângulo\(t\) com base na Figura\(\PageIndex{9}\).

Figura\(\PageIndex{9}\)

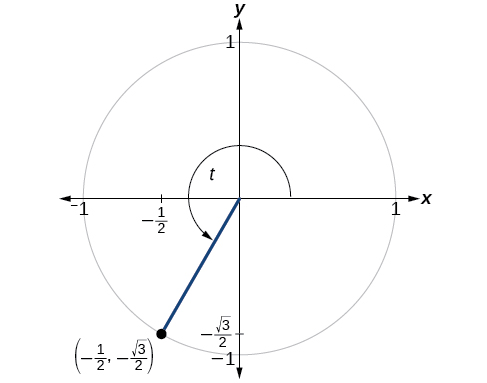
Solução

\[\begin{align*} \sin t &= y=−\dfrac{\sqrt{3}}{2} \\ \cos t &=x =−\dfrac{1}{2} \\ \tan t &= \dfrac{ \sin t}{ \cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{−\frac{1}{2}}= \sqrt{3} \\ \sec t &= \dfrac{1}{\cos t} = \dfrac{1}{−\frac{1}{2}}=−2 \\ \csc t &= \dfrac{1}{\sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}=−\dfrac{2\sqrt{3}}{3} \\ \cot t &= \dfrac{1}{ \tan t}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercício\(\PageIndex{8}\)

Encontre os valores das seis funções trigonométricas do ângulo\(t\) com base na Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\)

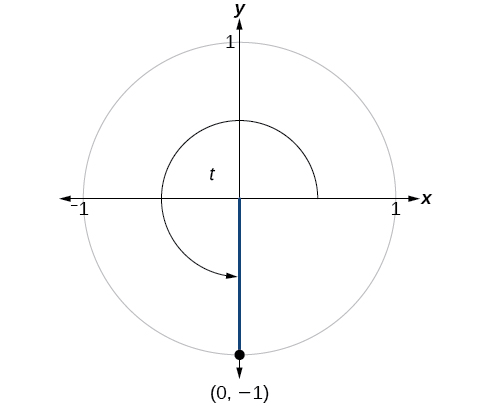
Solução

\(\begin{align} \sin t &=−1, \cos t=0, \tan t= \text{Undefined} \\ \\sec t &= \text{Undefined}, \csc t=−1, \cot t=0 \end{align}\)

Exemplo\(\PageIndex{9}\): Finding the Value of Trigonometric Functions

Se\( \sin(t)=−\frac{\sqrt{3}}{2}\) e\( \cos (t)=\frac{1}{2}\), encontre\( \sec (t),\csc (t),\tan (t), \cot (t).\)

Solução

\[ \begin{align} \sec t &= \dfrac{1}{ \cos t}= \dfrac{1}{\frac{1}{2}}=2 \\ \csc t &= \dfrac{1}{ \sin t}= \dfrac{1}{−\frac{\sqrt{3}}{2}}−\dfrac{2\sqrt{3}}{3} \\ \tan t &= \dfrac{\sin t}{\cos t}=\dfrac{−\frac{\sqrt{3}}{2}}{\frac{1}{2}}=−\sqrt{3} \\ \cot t &= \dfrac{1}{ \tan t}= \dfrac{1}{−\sqrt{3}}=−\dfrac{\sqrt{3}}{3} \end{align}\]

Exercício\(\PageIndex{9}\):

Se\(\sin (t)= \frac{\sqrt{2}}{2}\)\( \sec (t), \csc (t),\tan (t),\) e\(\cos (t)=\frac{\sqrt{2}}{2},\) encontre\( \cot (t)\) e.

Solução

\( \sec t= \sqrt{2},\csc t=\sqrt{2}, \tan t=1, \cot t=1\)

Cálculo de funções trigonométricas com uma calculadora

Aprendemos como avaliar as seis funções trigonométricas para os ângulos comuns do primeiro quadrante e usá-las como ângulos de referência para ângulos em outros quadrantes. Para avaliar funções trigonométricas de outros ângulos, usamos uma calculadora científica ou gráfica ou um software de computador. Se a calculadora tiver um modo de graus e um modo radiano, confirme se o modo correto foi escolhido antes de fazer um cálculo.

Avaliar uma função tangente com uma calculadora científica em vez de uma calculadora gráfica ou sistema de álgebra computacional é como avaliar um seno ou cosseno: insira o valor e pressione a tecla TAN. Para as funções recíprocas, pode não haver nenhuma chave dedicada que diga CSC, SEC ou COT. Nesse caso, a função deve ser avaliada como a recíproca de um seno, cosseno ou tangente.

Se precisarmos trabalhar com graus e nossa calculadora ou software não tiver um modo de graduação, podemos inserir os graus multiplicados pelo fator de conversão\(\frac{π}{180}\) para converter os graus em radianos. Para encontrar a secante de\( 30°\), poderíamos pressionar

\[\mathrm{(for \; a \; scientific \; calculator):\dfrac{1}{30×\frac{π}{180}}COS }\]

ou

\[ \mathrm{(for \; a \; graphing \; calculator): \dfrac{1}{cos(\frac{30π}{180})} }\]

como: Dada uma medida de ângulo em radianos, use uma calculadora científica para encontrar a cossecante

1. Se a calculadora tiver o modo de graus e o modo radiano, configure-a para o modo radiano.
2. Entrar:\(1 \; / \)
3. Insira o valor do ângulo entre parênteses.
4. Pressione a tecla SIN.
5. Pressione a tecla =.

como: Dada uma medida de ângulo em radianos, use um utilitário/calculadora gráfica para encontrar a cossecante

1. Se o utilitário gráfico tiver o modo de graus e o modo radiano, configure-o para o modo radiano.
2. Entrar:\(1 \; /\)
3. Pressione a tecla SIN.
4. Insira o valor do ângulo entre parênteses.
5. Pressione a tecla ENTER.

Exemplo\(\PageIndex{10}\): Evaluating the Cosecant Using Technology

Avalie a cossecante de\(\frac{5π}{7}\).

Solução

Para uma calculadora científica, insira as informações a seguir:

\[ \mathrm{1 / ( 5 × π / 7 ) SIN =}\]

\[ \mathrm{ \csc (\dfrac{5π}{7})≈1.279} \]

Exercício\(\PageIndex{10}\):

Avalie a cotangente de\(−\frac{π}{8}\).

\(≈−2.414\)

meios de comunicação

Acesse esses recursos on-line para obter instruções adicionais e praticar com outras funções trigonométricas.

• Determinando valores da função trigonomé
• Mais exemplos de determinação de funções trigonométricas
• Identidades pitagóricas
• Funções trigonométricas em uma calculadora

Equações-chave

Função tangente	\( \tan t= \frac{ \sin t}{\cos t}\)
Função secante	\( \sec t= \frac{1}{ \cos t}\)
Função cossecante	\( \csc t= \frac{1}{ \sin t}\)
Função cotangente	\( \cot t= \frac{1}{\tan t}= \frac{\cos t}{ \sin t}\)

Conceitos-chave

• A tangente de um ângulo é a razão entre o valor y e o valor x do ponto correspondente no círculo unitário.
• A secante, a cotangente e a cossecante são todas recíprocas de outras funções. A secante é a recíproca da função cosseno, a cotangente é a recíproca da função tangente e a cossecante é a recíproca da função seno.
• As seis funções trigonométricas podem ser encontradas a partir de um ponto no círculo unitário. Veja o exemplo.
• As funções trigonométricas também podem ser encontradas a partir de um ângulo. Veja o exemplo.
• As funções trigonométricas de ângulos fora do primeiro quadrante podem ser determinadas usando ângulos de referência. Veja o exemplo.
• Diz-se que uma função é par se\(f(−x)=f(x)\) e ímpar se\(f(−x)=−f(x)\).
• Cosseno e secante são pares; seno, tangente, cossecante e cotangente são ímpares.
• Propriedades pares e ímpares podem ser usadas para avaliar funções trigonométricas. Veja o exemplo.
• A identidade pitagórica torna possível encontrar um cosseno a partir de um seno ou um seno de um cosseno.
• As identidades podem ser usadas para avaliar funções trigonométricas. Veja o exemplo e o exemplo.
• Identidades fundamentais, como a identidade pitagórica, podem ser manipuladas algebricamente para produzir novas identidades. Veja o exemplo.
• As funções trigonométricas se repetem em intervalos regulares.
• O período\(P\) de uma função de repetição f f é o menor intervalo, tal como\(f(x+P)=f(x)\) para qualquer valor de\(x\).
• Os valores das funções trigonométricas de ângulos especiais podem ser encontrados por análise matemática.
• Para avaliar funções trigonométricas de outros ângulos, podemos usar uma calculadora ou um software de computador. Veja o exemplo.

Glossário

cossecante

o recíproco da função seno: no círculo unitário,\( \csc t=\frac{1}{y},y≠0\)

cotangente

o inverso da função tangente: no círculo unitário,\( \cot t= \frac{x}{y},y≠0\)

identidades

afirmações que são verdadeiras para todos os valores da entrada na qual estão definidas

período

o menor intervalo\(P\) de uma função de repetição\(f\) tal que\(f(x+P)=f(x)\)

secante

o recíproco da função cosseno: no círculo unitário,\( \sec t= \frac{1}{x},x≠0 \)

tangente

o quociente do seno e do cosseno: no círculo unitário,\( \tan t= \frac{y}{x},x≠0\)