4.E: Funções exponenciais e logarítmicas (exercícios)
- Page ID
- 189222
4.1: Funções exponenciais
Quando as populações crescem rapidamente, costumamos dizer que o crescimento é “exponencial”, o que significa que algo está crescendo muito rapidamente. Para um matemático, no entanto, o termo crescimento exponencial tem um significado muito específico. Nesta seção, examinaremos as funções exponenciais, que modelam esse tipo de crescimento rápido.
Verbal
1) Explique por que os valores de uma função exponencial crescente acabarão por ultrapassar os valores de uma função linear crescente.
- Resposta:
-
As funções lineares têm uma taxa de mudança constante. As funções exponenciais aumentam com base em uma porcentagem do original.
2) Dada uma fórmula para uma função exponencial, é possível determinar se a função cresce ou decai exponencialmente apenas observando a fórmula? Explique.
3) O Dicionário Oxford define a palavra nominal como um valor que é “declarado ou expresso, mas não necessariamente correspondente exatamente ao valor real”. Desenvolva um argumento razoável sobre por que o termo taxa nominal é usado para descrever a taxa percentual anual de uma conta de investimento que gera juros.
- Resposta:
-
Quando os juros são compostos, a porcentagem de juros auferidos em relação ao principal acaba sendo maior do que a taxa percentual anual da conta de investimento. Assim, a taxa percentual anual não corresponde necessariamente aos juros reais auferidos, que é a própria definição de nominal.
Algébrico
Para os exercícios a seguir, identifique se a declaração representa uma função exponencial. Explique.
4) O aumento médio anual da população de uma matilha de lobos é\(25\).
5) Uma população de bactérias diminui em um fator a\(\frac{1}{8}\) cada\(24\) hora.
- Resposta:
-
exponencial; a população diminui em uma taxa proporcional.
6) O valor de uma coleção de moedas aumentou em\(3.25\%\)
7) Para cada sessão de treinamento, um personal trainer cobra\(\$5\) menos de seus clientes do que a sessão de treinamento anterior.
- Resposta:
-
não exponencial; a carga diminui em uma quantidade constante a cada visita, então a declaração representa uma função linear.
8) A altura de um projétil no momento\(t\) é representada pela função\(h(t)= -4.9t^2 + 18t + 40\)
Para os exercícios a seguir, considere este cenário: Para cada ano \(t\), a população de uma floresta de árvores é representada pela função \(A(t)=115(1.025)^t\).
9) Qual população florestal está crescendo em um ritmo mais rápido?
- Resposta:
-
A floresta representada pela função\(B(t)=82(1.029)^t\).
10) Qual floresta tinha um número maior de árvores inicialmente? Por quantos?
11) Supondo que os modelos de crescimento populacional continuem representando o crescimento das florestas, qual floresta terá um maior número de árvores após\(20\) anos? Por quantos?
- Resposta:
-
Depois de\(t=20\) anos, a floresta A terá\(43\)
12) Supondo que os modelos de crescimento populacional continuem representando o crescimento das florestas, cuja floresta terá um maior número de árvores depois\(100\)
13) Discuta os resultados acima dos quatro exercícios anteriores. Supondo que os modelos de crescimento populacional continuem representando o crescimento das florestas, qual floresta terá o maior número de árvores a longo prazo? Por quê? Quais são alguns fatores que podem influenciar a validade de longo prazo do modelo de crescimento exponencial?
- Resposta:
-
As respostas podem variar. Resposta da amostra: Por vários anos, a população da floresta A excederá cada vez mais a floresta B, mas como a floresta B realmente cresce a uma taxa mais rápida, a população acabará se tornando maior do que a floresta A e permanecerá assim enquanto os modelos de crescimento populacional se mantiverem. Alguns fatores que podem influenciar a validade de longo prazo do modelo de crescimento exponencial são a seca, uma epidemia que abate a população e outros fatores ambientais e biológicos.
Para os exercícios a seguir, determine se a equação representa crescimento exponencial, declínio exponencial ou nenhum dos dois. Explique.
14)\(y=300(1−t)^5\)
15)\(y=220(1.06)^x\)
- Resposta:
-
crescimento exponencial; O fator de crescimento,\(1.06\) é maior que\(1\).
16)\(y=16.5(1.025)^{\frac{1}{x}}\)
17)\(y=11,701(0.97)^t\)
- Resposta:
-
decaimento exponencial; O fator de decaimento,\(0.97\)
, .
Para os exercícios a seguir, encontre a fórmula para uma função exponencial que passa pelos dois pontos dados.
18) (\(0,6)\)e\((3,750)\)
19)\((0,2000)\)
- Resposta:
-
\(f(x)=2000(0.1)^x\)
20)\(\left (−1,\frac{3}{2} \right )\) e\((3,24)\)
21)\((−2,6)\)
- Resposta:
-
\(f(x)=\left ( \frac{1}{6} \right )^{-\frac{3}{5}} \left ( \frac{1}{6} \right )^{\frac{x}{5}}\approx 2.93 (0.699)^x\)
22)\((3,1)\) e\((5,4)\)
Para os exercícios a seguir, determine se a tabela pode representar uma função linear, exponencial ou nenhuma das duas. Se parecer exponencial, encontre uma função que passe pelos pontos.
23)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(f(x)\) | 70 | 40 | 10 | -20 |
- Resposta:
-
Linear
24)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(h(x)\) | 70 | 49 | 34,3 | 24,01 |
25)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(m(x)\) | 80 | 61 | 42,9 | 25,61 |
- Resposta:
-
Nem
26)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(f(x)\) | 10 | 20 | 40 | 80 |
27)
| \(x\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(g(x)\) | -3,25 | 2 | 7.25 | 12,5 |
- Resposta:
-
Linear
Para os exercícios a seguir, use a fórmula de juros compostos,\(A(t)=P\left (1+ \frac{r}{n} \right )^{nt}\)
28) Após um certo número de anos, o valor de uma conta de investimento é representado pela equação\(10,250\left (1+ \frac{0.04}{12} \right )^{120}\)
29) Qual foi o depósito inicial feito na conta no exercício anterior?
- Resposta:
-
\(\$10,250\)
30) Há quantos anos a conta do exercício anterior estava acumulando juros?
31) Uma conta é aberta com um depósito inicial de\(\$6,500\) e rende\(3.6\%\) juros compostos semestralmente. Quanto valerá a conta em\(20\) anos?
- Resposta:
-
\(\$13,268.58\)
32) Quanto mais valeria a conta no exercício anterior se os juros fossem aumentados semanalmente?
33) Resolva a fórmula de juros compostos para o principal,\(P\).
- Resposta:
-
\(P=A(t)\cdot \left (1+ \frac{r}{n} \right )^{-nt}\)
34) Use a fórmula encontrada no exercício anterior para calcular o depósito inicial de uma conta que vale\(\$14,472.74\) após o ganho\(5.5\%\)
35) Quanto mais valeria a conta nos dois exercícios anteriores se estivesse ganhando juros por\(5\) mais anos?
- Resposta:
-
\(\$4,572.56\)
36) Use propriedades de expoentes racionais para resolver a fórmula de juros compostos para a taxa de juros,\(r\).
37) Use a fórmula encontrada no exercício anterior para calcular a taxa de juros de uma conta que foi composta semestralmente, teve um depósito inicial de\(\$9,000\) e valeu\(\$13,373.53\) após\(10\) anos.
- Resposta:
-
\(4\%\)
38) Use a fórmula encontrada no exercício anterior para calcular a taxa de juros de uma conta que foi composta mensalmente, teve um depósito inicial de\(\$5,500\) e valeu\(30\) anos\(\$38,455\) depois.
Para os exercícios a seguir, determine se a equação representa crescimento contínuo, decaimento contínuo ou nenhum dos dois. Explique.
39)\(y=3742(e)^{0.75t}\)
- Resposta:
-
crescimento contínuo; a taxa de crescimento é maior que\(0\).
40)\(y=150(e)^{\frac{3.25}{t}}\)
41)\(y=2.25(e)^{-2t}\)
- Resposta:
-
decadência contínua; a taxa de crescimento é menor que\(0\).
42) Suponha que uma conta de investimento seja aberta com um depósito inicial de\(\$12,000\) ganhos\(7.2\%\)
43) Quanto menos valeria a conta do Exercício 42 após\(30\) anos se fosse composta mensalmente?
- Resposta:
-
\(\$669.42\)
Numérico
Para os exercícios a seguir, avalie cada função. Arredonde as respostas para quatro casas decimais, se necessário.
44)\(f(x)=2(5)^x\) para\(f(-3)\)
45)\(f(x)=-4^{2x+3}\) para\(f(-1)\)
- Resposta:
-
\(f(-1)=-4\)
46)\(f(x)=e^x\), para\(f(3)\)
47)\(f(x)=-2e^{x-1}\), para\(f(-1)\)
- Resposta:
-
\(f(-1)\approx -0.2707\)
48)\(f(x)=2.7(4)^{-x+1}+1.5\), para\(f(-2)\)
49)\(f(x)=1.2e^{2x}-0.3\), para\(f(3)\)
- Resposta:
-
\(f(3)\approx 483.8146\)
50)\(f(x)=-\frac{3}{2}(3)^{-x}+\frac{3}{2}\), para\(f(2)\)
Tecnologia
Para os exercícios a seguir, use uma calculadora gráfica para encontrar a equação de uma função exponencial dados os pontos na curva.
51)\((0,3)\) e\((3,375)\)
- Resposta:
-
\(y=3\cdot 5^x\)
52)\((3,222.62)\) e\((10,77.456)\)
53)\((20,29.495)\) e\((150,730.89)\)
- Resposta:
-
\(y\approx 18\cdot 1.025^x\)
54)\((5,2.909)\) e\((13,0.005)\)
55) ((11.310.035)\) e\((25,356.3652)\)
- Resposta:
-
\(y\approx 0.2\cdot 1.95^x\)
Extensões
56) O rendimento percentual anual (APY) de uma conta de investimento é uma representação da taxa de juros real obtida em uma conta de composição. É baseado em um período de composição de um ano. Mostre que o APY de uma conta que aumenta mensalmente pode ser encontrado com a fórmula\(APY=\left (1+\frac{r}{12} \right )^{12}-1\)
57) Repita o exercício anterior para encontrar a fórmula para o APY de uma conta que se acumula diariamente. Use os resultados deste e do exercício anterior para desenvolver uma função\(I(n)\)
- Resposta:
-
\(\begin{align*} APY &= \frac{A(t)-a}{a}\\ &= \frac{a\left ( 1+\frac{r}{365} \right )^{365(1)}-a}{a}\\ &= \frac{a\left [\left ( 1+\frac{r}{365} \right )^{365}-1 \right ]}{a}\\ &= \left ( 1+\frac{r}{365} \right )^{365}-1 \end{align*}\);\(I(n)=\left ( 1+\frac{r}{n} \right )^n - 1\)
58) Lembre-se de que uma função exponencial é qualquer equação escrita na\(f(x)=a\cdot b^x\) forma que\(a\) e\(b\) são números positivos\(b≠1\) e. Qualquer número positivo\(b\)
59) Em uma função de decaimento exponencial, a base do expoente é um valor entre\(0\)\(1\) e. Assim, para algum número\(b>1\),
- Resposta:
-
\(f\)Seja a função de decaimento exponencial\(f(x)=a\cdot \left (\frac{1}{b} \right )^x\) tal que\(b>1\). Então, para algum número\(n>0\),
\(\begin{align*} f(x) &= a\cdot \left (\frac{1}{b} \right )^x \\ &= a \left (b^{-1} \right )^x\\ &= a\left ( (e^n)^{-1} \right )^x\\ &= a\left ( e^{-n} \right )^x\\ &= a(e)^{-nx} \end{align*}\)
60) A fórmula para o valor\(A\) em uma conta de investimento com uma taxa de juros nominal a qualquer\(r\) momento\(t\) é dada por\(A(t)=a(e)^{rt}\), onde\(a\)
Aplicativos do mundo real
61) A população de raposas em uma determinada região tem uma taxa de crescimento anual de\(9\%\) por ano. No ano de 2012, foram contadas\(23,900\) raposas na área. Qual é a previsão da população de raposas no ano de 2020?
- Resposta:
-
\(47,622\)raposa
62) Um cientista começa com\(100\) miligramas de uma substância radioativa que decai exponencialmente. Depois de\(35\) horas, restam\(50\) mg da substância. Quantos miligramas permanecerão após o\(54\) expediente?
63) No ano de 1985, uma casa foi avaliada em\(\$110,000\). No ano de 2005, o valor havia se valorizado para\(\$145,000\). Qual foi a taxa de crescimento anual entre 1985 e 2005? Suponha que o valor continuou a crescer na mesma porcentagem. Qual foi o valor da casa no ano de 2010?
- Resposta:
-
\(1.39\%\);\(\$155,368.09\)
64) Um carro foi avaliado em\(\$38,000\) no ano de 2007. Em 2013, o valor havia se depreciado para\(\$11,000\) Se o valor do carro continuar caindo na mesma porcentagem, quanto valerá em 2017?
65) Jamal quer economizar\(\$54,000\) para pagar a entrada de uma casa. Quanto ele precisará investir em uma conta na\(8.2\%\) APR, composta diariamente, para atingir sua meta em\(5\) anos?
- Resposta:
-
\(\$35,838.76\)
66) Kyoko tem o\(\$10,000\) que ela quer investir. Seu banco tem várias contas de investimento para escolher, todas compostas diariamente. Seu objetivo é ter\(\$15,000\) até o final da pós-graduação em\(6\) anos. Até o centésimo de um por cento mais próximo, qual deve ser sua taxa de juros anual mínima para atingir sua meta? (Dica: resolva a fórmula de juros compostos para a taxa de juros.)
67) Alyssa abriu uma conta de aposentadoria na\(7.25\%\) APR no ano 2000. Seu depósito inicial foi\(\$13,500\). Quanto valerá a conta em 2025 se os juros aumentarem mensalmente? Quanto mais ela ganharia se os juros aumentassem continuamente?
- Resposta:
-
\(\$82,247.78\);\(\$449.75\)
68) Uma conta de investimento com uma taxa de juros anual de\(7\%\) foi aberta com um depósito inicial de\(\$4,000\) Compare os valores da conta após\(9\) anos em que os juros são compostos anualmente, trimestralmente, mensalmente e continuamente.
4.2: Gráficos de funções exponenciais
Conforme discutimos na seção anterior, as funções exponenciais são usadas para muitas aplicações do mundo real, como finanças, ciência forense, ciência da computação e a maioria das ciências da vida. Trabalhar com uma equação que descreve uma situação do mundo real nos dá um método para fazer previsões. Na maioria das vezes, no entanto, a equação em si não é suficiente. Aprendemos muito sobre as coisas vendo suas representações pictóricas, e é exatamente por isso que representar graficamente equações exponenciais é uma ferramenta poderosa.
Verbal
1) Qual o papel da assíntota horizontal de uma função exponencial ao nos contar sobre o comportamento final do gráfico?
- Resposta:
-
Uma assíntota é uma linha à qual o gráfico de uma função se aproxima, à medida que aumenta\(x\) ou diminui sem limite. A assíntota horizontal de uma função exponencial nos diz o limite dos valores da função à medida que a variável independente fica extremamente grande ou extremamente pequena.
2) Qual é a vantagem de saber reconhecer algebricamente as transformações do gráfico de uma função parental?
Algébrico
3) O gráfico de\(f(x) = 3^x\)
- Resposta:
-
\(g(x)=4(3)^{-x}\)
; intercepção y: ;
4) O gráfico de\(f(x)=\left ( \frac{1}{2} \right )^{-x}\)
5) O gráfico de\(f(x)=10^x\) é refletido sobre o\(x\) eixo -e deslocado em\(7\) unidades ascendentes. Qual é a equação da nova função,\(g(x)\)?
- Resposta:
-
\(g(x)=-10^x + 7\);\(y\) -intercept:\((0,6)\); Domínio: todos os números reais; Alcance: todos os números reais menores que\(7\).
6) O gráfico de\(3\) unidades para a direita\(f(x)=(1.68)^x\) é deslocado, esticado verticalmente por um fator de\(2\)
7) O gráfico de\(2\) unidades à esquerda\(f(x)=2\left ( \frac{1}{4} \right )^{x-20}\) é deslocado, esticado verticalmente por um fator de\(4\)
- Resposta:
-
\(g(x)=2\left ( \frac{1}{4} \right )^x\);\(y\) -interceptar:\((0,2)\);
Gráfica
Para os exercícios a seguir, represente graficamente a função e sua reflexão sobre o\(y\) eixo -nos mesmos eixos e forneça o\(y\) intercepto -.
8)\(f(x)=3\left ( \frac{1}{2} \right )^x\)
9)\(g(x)=-2(0.25)^x\)
- Resposta:
-
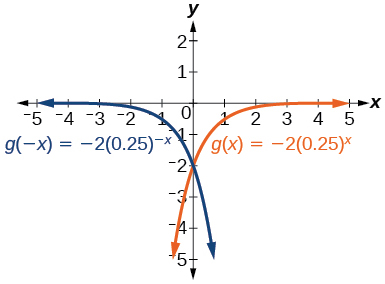
\(y\)-interceptar:\((0,-2)\)
10)\(h(x)=6(1.75)^{-x}\)
Para os exercícios a seguir, represente graficamente cada conjunto de funções nos mesmos eixos.
11)\(f(x)=3\left ( \frac{1}{4} \right )^x, g(x)=3(2)^x, h(x)=3(4)^x\)
- Resposta:
-
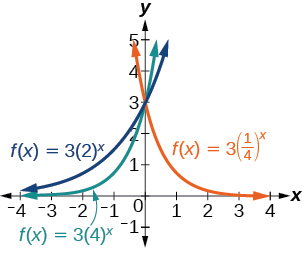
12)\(f(x)=\frac{1}{4}(3)^x, g(x)=2(3)^x, h(x)=4(3)^x\)
Para os exercícios a seguir, combine cada função com um dos gráficos na Figura abaixo.
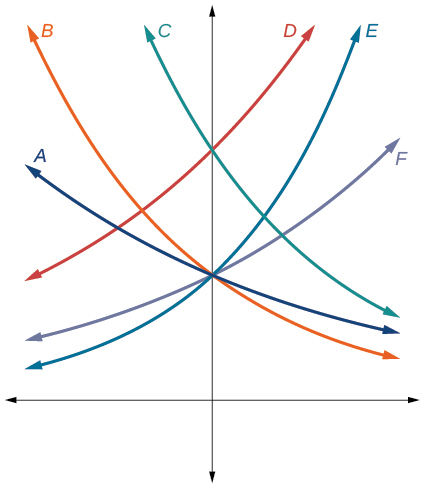
13)\(f(x)=2(0.69)^x\)
- Resposta:
-
B
14)\(f(x)=2(1.28)^x\)
15)\(f(x)=2(0.81)^x\)
- Resposta:
-
UMA
16)\(f(x)=4(1.28)^x\)
17)\(f(x)=2(1.59)^x\)
- Resposta:
-
E
18)\(f(x)=4(0.69)^x\)
Para os exercícios a seguir, use os gráficos mostrados na Figura abaixo. Todos têm o formulário\(f(x)=ab^x\).
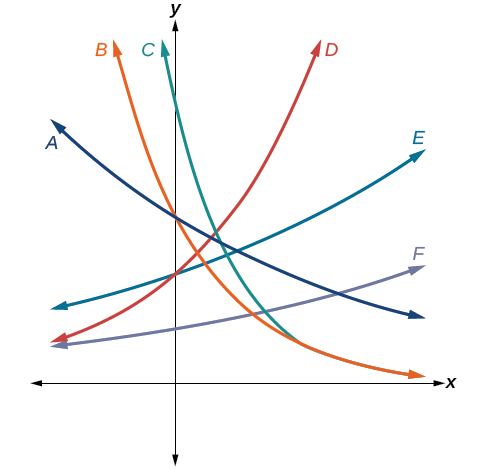
19) Qual gráfico tem o maior valor para\(b\)?
- Resposta:
-
D
20) Qual gráfico tem o menor valor para\(b\)?
21) Qual gráfico tem o maior valor para\(a\)?
- Resposta:
-
C
22) Qual gráfico tem o menor valor para\(a\)?
Para os exercícios a seguir, represente graficamente a função e sua reflexão sobre o\(x\) eixo -nos mesmos eixos.
23)\(f(x)=\frac{1}{2}(4)^x\)
- Resposta:
-
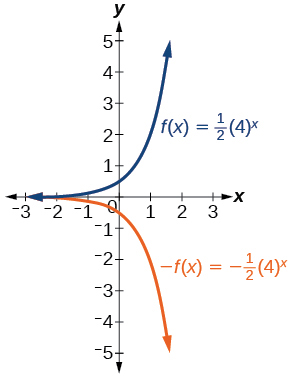
24)\(f(x)=3(0.75)^x-1\)
25)\(f(x)=-4(2)^x+2\)
- Resposta:
-
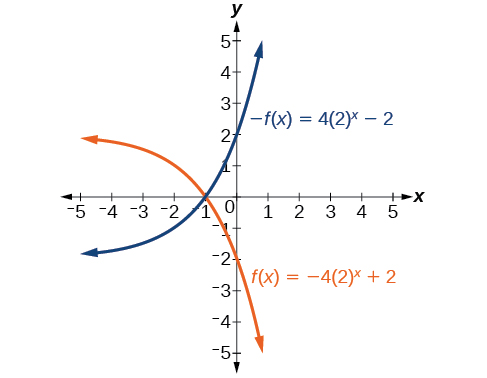
Para os exercícios a seguir, faça um gráfico da transformação de\(f(x)=2^x\)
26)\(f(x)=2^{-x}\)
27)\(h(x)=2^x+3\)
- Resposta:
-
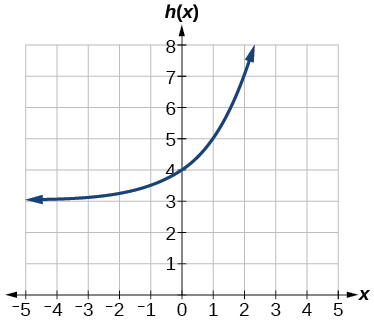
Assíntota horizontal:\(h(x)=3\)
;
28)\(f(x)=2^{x-2}\)
Para os exercícios a seguir, descreva o comportamento final dos gráficos das funções.
29)\(f(x)=-5(4)^x-1\)
- Resposta:
-
Como\(x\rightarrow \infty , f(x)\rightarrow -\infty\)
Como\(x\rightarrow -\infty , f(x)\rightarrow -1\)
30)\(f(x)=3\left ( \frac{1}{2} \right )^x-2\)
31)\(f(x)=3(4)^{-x}+2\)
- Resposta:
-
Como\(x\rightarrow \infty , f(x)\rightarrow 2\)
Como\(x\rightarrow -\infty , f(x)\rightarrow \infty\)
Para os exercícios a seguir, comece com o gráfico de\(f(x)=4^x\)
32) Desloque\(f(x)\)\(4\) as unidades para cima
33) Deslocar\(f(x)\) \(3\) units para baixo
- Resposta:
-
\(f(x)=4^x-3\)
34) Deslocar\(f(x)\)\(2\) unidades para a esquerda
35) Mude\(f(x)\)\(5\) as unidades para a direita
- Resposta:
-
\(f(x)=4^{x-5}\)
36) Reflita\(f(x)\) sobre o\(x\) eixo -
37) Reflita\(f(x)\) sobre o\(y\) eixo -
- Resposta:
-
\(f(x)=4^{-x}\)
Para os exercícios a seguir, cada gráfico é uma transformação de\(f(x)=2^x\)
38)
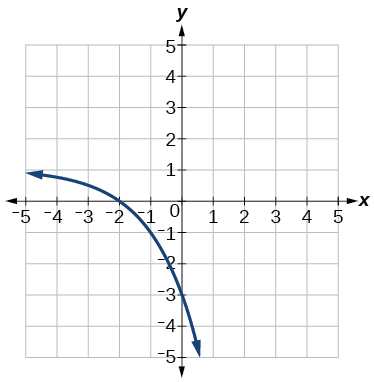
39)
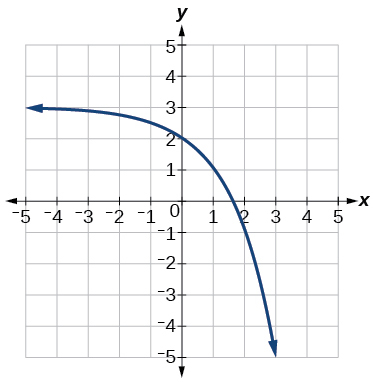
- Resposta:
-
\(y=-2^x+3\)
40)
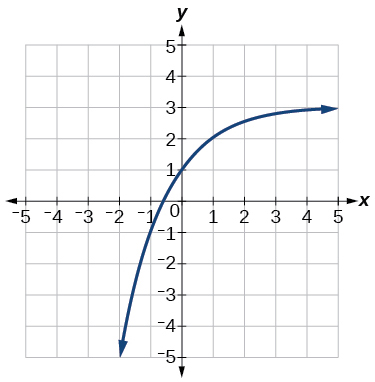
Para os exercícios a seguir, encontre uma equação exponencial para o gráfico.
41)
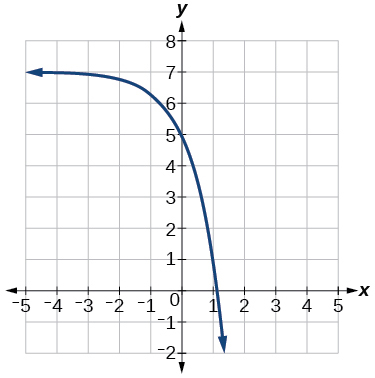
- Resposta:
-
\(y=-2(3)^x+7\)
(42)
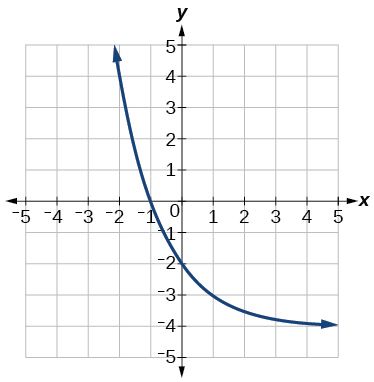
Numérico
Para os exercícios a seguir, avalie as funções exponenciais para o valor indicado de\(x\).
43)\(g(x)=\frac{1}{3}(7)^{x-2}\) para\(g(6)\).
- Resposta:
-
\(g(6)=800+\frac{1}{3}\approx 800.3333\)
44)\(f(x)=4(2)^{x-1}-2\) para\(f(5)\).
45)\(h(x)=-\frac{1}{2}\left ( \frac{1}{2} \right )^x+6\) para\(h(-7)\).
- Resposta:
-
\(h(-7)=-58\)
Tecnologia
Para os exercícios a seguir, use uma calculadora gráfica para aproximar as soluções da equação. Arredonde para o milésimo mais próximo.
(46)\(-50=\left ( \frac{1}{2} \right )^{-x}\)
47)\(116=\left ( \frac{1}{4} \right )\left ( \frac{1}{8} \right )^x\)
- Resposta:
-
\(x\approx -2.953\)
48)\(12=2(3)^x+1\)
49)\(5=3\left ( \frac{1}{2} \right )^{x-1}-2\)
- Resposta:
-
\(x\approx -0.222\)
50)\(-30=-4(2)^{x+2}+2\)
Extensões
51) Explore e discuta os gráficos de\(F(x)=(b)^x\)\(G(x)=\left ( \frac{1}{b} \right )^x\) e. Em seguida, faça uma conjectura sobre a relação entre os gráficos das funções\(b^x\) e\(\left ( \frac{1}{b} \right )^x\) para qualquer número real\(b>0\).
- Resposta:
-
O gráfico de\(G(x)=\left ( \frac{1}{b} \right )^x\) é a reflexão sobre o\(y\) eixo -do gráfico de\(F(x)=(b)^x\); Para qualquer número real\(b>0\) e função\(f(x)=(b)^x\)
,
52) Prove a conjectura feita no exercício anterior.
53) Explore e discuta os gráficos de\(f(x) = 4^x\)\(g(x)=4^{x-2}\), e\(h(x)=\left ( \frac{1}{16} \right )4^x\)
- Resposta:
-
Os gráficos de\(g(x)\) e\(h(x)\) são iguais e são um deslocamento horizontal à direita do gráfico de\(f(x)\); Para qualquer número real\(n\)\(b>0\), número real e função\(f(x)=b^x\)
,
54) Prove a conjectura feita no exercício anterior.
4.3: Funções logarítmicas
O inverso de uma função exponencial é uma função logarítmica e o inverso de uma função logarítmica é uma função exponencial.
Verbal
1) O que é um\(b\) logaritmo base? Discuta o significado interpretando cada parte das equações equivalentes\(b^y=x\) e\(\log _bx=y\) para\(b>0, b\neq 1\).
- Resposta
-
Um logaritmo é um expoente. Especificamente, é o expoente ao qual uma base\(b\) é elevada para produzir um determinado valor. Nas expressões dadas, a base\(b\) tem o mesmo valor. O expoente,\(y\)
, ,
2) Como a função logarítmica está\(f(x)=\log _bx\) relacionada à função exponencial\(g(x)=b^x\)? Qual é o resultado da composição dessas duas funções?
3) Como a equação logarítmica pode\(\log _bx=y\) ser resolvida\(x\) usando as propriedades dos expoentes?
- Resposta
-
Como a equação de um logaritmo é equivalente a uma equação exponencial, o logaritmo pode ser convertido na equação exponencial\(b^y = x\)
, .
4) Discuta o significado do logaritmo comum. Qual é sua relação com um logaritmo com base\(b\)
5) Discuta o significado do logaritmo natural. Qual é sua relação com um logaritmo com base\(b\)
- Resposta
-
O logaritmo natural é um caso especial do logaritmo com base\(b\) em que o log natural sempre tem base\(e\).
, .
Algébrico
Para os exercícios a seguir, reescreva cada equação na forma exponencial.
6)\(\log_{4}(q)=m\)
7)\(\log_{a}(b)=c\)
- Resposta
-
\(a^c=b\)
8)\(\log_{16}(y)=x\)
9)\(\log_{x}(64)=y\)
- Resposta
-
\(x^y=64\)
10)\(\log_{y}(x)=-11\)
11)\(\log_{15}(a)=b\)
- Resposta
-
\(15^b=a\)
12)\(\log_{y}(137)=x\)
13)\(\log_{13}(142)=a\)
- Resposta
-
\(13^a=142\)
14)\(\log(v)=t\)
15)\(\ln(w)=n\)
- Resposta
-
\(e^n=w\)
Para os exercícios a seguir, reescreva cada equação na forma logarítmica.
16)\(4^x=y\)
17)\(c^d=k\)
- Resposta
-
\(\log_{c}(k)=d\)
18)\(m^{-7}=n\)
19)\(19^x=y\)
- Resposta
-
\(\log_{19}(y)=x\)
20)\(x^{-\frac{10}{13}}=y\)
21)\(n^4 = 103\)
- Resposta
-
\(\log_{n}(103)=4\)
22)\(\left ( \dfrac{7}{5} \right )^m=n\)
23)\(y^x=\dfrac{39}{100}\)
- Resposta
-
\(\log_{y}\left ( \dfrac{39}{100} \right )=x\)
24)\(10^a=b\)
25)\(e^k=h\)
- Resposta
-
\(\ln(w)=n\)
Para os exercícios a seguir, resolva\(x\) por convertendo a equação logarítmica na forma exponencial.
26)\(\log_{3}(x)=2\)
27)\(\log_{2}(x)=-3\)
- Resposta
-
\(x=2^{-3}=\dfrac{1}{8}\)
28)\(\log_{5}(x)=2\)
29)\(\log_{3}(x)=3\)
- Resposta
-
\(x = 3^3 = 27\)
30)\(\log_{2}(x)=6\)
31)\(\log_{9}(x)=\dfrac{1}{2}\)
- Resposta
-
\(x=9^{\frac{1}{2}}=3\)
32)\(\log_{18}(x)=2\)
33)\(\log_{6}(x)=-3\)
- Resposta
-
\(x=6^{-3}=\dfrac{1}{216}\)
34)\(\log (x)=3\)
(35)\(\ln(x)=2\)
- Resposta
-
\(x=e^2\)
Para os exercícios a seguir, use a definição de logaritmos comuns e naturais para simplificar.
36)\(\log (100^8)\)
37)\(10^{\log (32)}\)
- Resposta
-
\(32\)
38)\(2\log (.0001)\)
39)\(e^{\ln (1.06)}\)
- Resposta
-
\(1.06\)
40)\(\ln (e^{-5.03})\)
41)\(e^{\ln (10.125)}+4\)
- Resposta
-
\(14.125\)
Numérico
Para os exercícios a seguir, avalie a expressão\(b\) logarítmica básica sem usar uma calculadora.
(42)\(\log _3\left ( \frac{1}{27} \right )\)
43)\(\log _6(\sqrt{6})\)
- Resposta
-
\(\dfrac{1}{2} \)
44)\(\log _2\left ( \frac{1}{8} \right )+4\)
45)\(6\log _8(4)\)
- Resposta
-
\(4\)
Para os exercícios a seguir, avalie a expressão logarítmica comum sem usar uma calculadora.
(46)\(\log (10,000)\)
47)\(\log (0.001)\)
- Resposta
-
\(-3\)
48)\(\log (1)+7\)
49)\(2\log (100^{-3})\)
- Resposta
-
\(-12\)
Para os exercícios a seguir, avalie a expressão logarítmica natural sem usar uma calculadora.
50)\(\ln \left ( e^{\frac{1}{3}} \right )\)
51)\(\ln (1)\)
- Resposta
-
\(0\)
52)\(\ln \left ( e^{-0.225} \right )-3\)
53)\(25\ln \left ( e^{\frac{2}{5}} \right )\)
- Resposta
-
\(10\)
Tecnologia
Para os exercícios a seguir, avalie cada expressão usando uma calculadora. Arredonde para o milésimo mais próximo.
54)\(\log (0.04)\)
55)\(\ln (15)\)
- Resposta
-
\(2.708\)
(56)\(\ln \left ( {\frac{4}{5}} \right )\)
57)\(\log (\sqrt{2})\)
- Resposta
-
\(0.151\)
(58)\(\ln (\sqrt{2})\)
Extensões
59) Está\(x=0\) no domínio da função\(f(x)=\log x\)? Em caso afirmativo, qual é o valor da função quando\(x=0\)? Verifique o resultado.
- Resposta
-
Não, a função não tem valor definido para\(x=0\)
. . . ,
60) Está\(f(x)=0\) na faixa da função\(f(x)=\log (x)\)?
61) Existe um número\(x\) assim\(\ln x = 2\)? Em caso afirmativo, qual é esse número? Verifique o resultado.
- Resposta
-
Sim. Suponha que exista um número real\(x\) tal que\(\ln x = 2\)
. , . .
62) O seguinte é verdadeiro:\(\frac{\log _3(27)}{\log _4\left ( \frac{1}{64} \right )}=-1\)
63) O seguinte é verdadeiro:\(\frac{\ln (e^{1.725})}{\ln (1)}=1.725\) Verifique o resultado.
- Resposta
-
Não;\(\ln (1) =0\), então\(\frac{\ln (e^{1.725})}{\ln (1)}=1.725\) é indefinido.
Aplicativos do mundo real
64) O índice de exposição\(EI\) de uma câmera\(35\) milimétrica é uma medida da quantidade de luz que atinge o filme. É determinado pela equação\(EI=\log _2\left ( \frac{f^2}{t} \right )\)
65) Consulte o exercício anterior. Suponha que o medidor de luz em uma câmera indique um\(EI\) dos\(-2\)
- Resposta
-
\(2\)
66) Os níveis\(I\) de intensidade de dois terremotos medidos em um sismógrafo podem ser comparados pela fórmula\(\log \left ( \frac{I_1}{I_2} \right )=M_1-M_2\)
4.4: Gráficos de funções logarítmicas
Nesta seção, discutiremos os valores para os quais uma função logarítmica é definida e, em seguida, voltaremos nossa atenção para a representação gráfica da família de funções logarítmicas.
Verbal
1) O inverso de cada função logarítmica é uma função exponencial e vice-versa. O que isso nos diz sobre a relação entre as coordenadas dos pontos nos gráficos de cada um?
- Resposta
-
Como as funções são inversas, seus gráficos são imagens espelhadas sobre a linha\(y-x\)
.
2) Que tipo (s) de tradução (ões), se houver, afetam o alcance de uma função logarítmica?
3) Que tipo (s) de tradução (ões), se houver, afetam o domínio de uma função logarítmica?
- Resposta
-
Deslocar a função para a direita ou para a esquerda e refletir a função sobre o\(y\) eixo -afetará seu domínio.
4) Considere a função logarítmica geral\(f(x)=\log _b(x)\)
5) O gráfico de uma função logarítmica geral tem uma assíntota horizontal? Explique.
- Resposta
-
Não. Uma assíntota horizontal sugeriria um limite no intervalo, e o alcance de qualquer função logarítmica na forma geral são todos números reais.
Algébrico
Para os exercícios a seguir, indique o domínio e o alcance da função.
6)\(f(x)=\log _3(x+4)\)
7)\(h(x)=\ln \left ( \dfrac{1}{2}-x \right )\)
- Resposta
-
Domínio:\(\left ( -\infty , \dfrac{1}{2} \right )\); Alcance:\((-\infty , \infty )\)
8)\(g(x)=\log _5(2x+9)-2\)
9)\(h(x)=\ln (4x+17)-5\)
- Resposta
-
Domínio:\(\left ( -\dfrac{17}{4}, \infty \right )\); Alcance:\((-\infty , \infty )\)
10)\(f(x)=\log _2 (12-3x)-3\)
Para os exercícios a seguir, indique o domínio e a assíntota vertical da função.
11)\(f(x)=\log _b (x-5)\)
- Resposta
-
Domínio:\((5, \infty )\); Assíntota vertical:\(x=5\)
12)\(g(x)=\ln (3-x)\)
13)\(f(x)=\log (3x+1)\)
- Resposta
-
Domínio:\(\left ( -\dfrac{1}{3}, \infty \right )\); Assíntota vertical:\(x=-\dfrac{1}{3}\)
14)\(f(x)=3\log (-x)+2\)
15)\(g(x)=-\ln (3x+9)-7\)
- Resposta
-
Domínio:\((-3, \infty )\); Assíntota vertical:\(x=-3\)
Para os exercícios a seguir, indique o domínio, a assíntota vertical e o comportamento final da função.
16)\(f(x)=\ln (2-x)\)
17)\(f(x)=\log \left ( x-\dfrac{3}{7} \right )\)
- Resposta
-
Domínio:\(\left ( \dfrac{3}{7},\infty \right )\)
Assíntota vertical:\(x=\dfrac{3}{7}\)
Comportamento final: como\(x\rightarrow \left (\dfrac{3}{7} \right )^+\)\(f(x)\rightarrow -\infty\) e como\(x\rightarrow \infty ,f(x)\rightarrow \infty\)
18)\(h(x)=-\log (3x-4)+3\)
19)\(g(x)=\ln (2x+6)-5\)
- Resposta
-
Domínio:\(\left ( -3,\infty \right )\)
Assíntota vertical:\(x=-3\)
Comportamento final: como\(x\rightarrow -3^+\)\(f(x)\rightarrow -\infty\) e como\(x\rightarrow \infty ,f(x)\rightarrow \infty\)
20)\(f(x)=\log_3 (15-5x)+6\)
Para os exercícios a seguir, indique o domínio, o intervalo e as interceptações x e y, se existirem. Se eles não existirem, escreva DNE.
21)\(h(x)=\log_4 (x-1)+1\)
- Resposta
-
Domínio:\(\left (1,\infty \right )\)
Alcance:\(-\infty , \infty \)
Assíntota vertical:\(x=1\)
\(x\)-interceptar:\(\left ( \dfrac{5}{4},0\right )\)
\(y\)-interceptação: DNE
22)\(f(x)=\log (5x+10)+3\)
23)\(g(x)=\ln (-x)-2\)
- Resposta
-
Domínio:\(\left (-\infty ,0 \right )\)
Alcance:\(-\infty , \infty \)
Assíntota vertical:\(x=0\)
\(x\)-interceptar:\(\left ( -e^2,0 \right )\)
\(y\)-interceptação: DNE
24)\(f(x)=\log_2 (x+2)-5\)
25)\(h(x)=3\ln (x)-9\)
- Resposta
-
Domínio:\(\left (0,\infty \right )\)
Alcance:\(-\infty , \infty \)
Assíntota vertical:\(x=0\)
\(x\)-interceptar:\(\left ( e^3,0 \right )\)
\(y\)-interceptação: DNE
Gráfica
Para os exercícios a seguir, combine cada função na Figura abaixo com a letra correspondente ao seu gráfico.
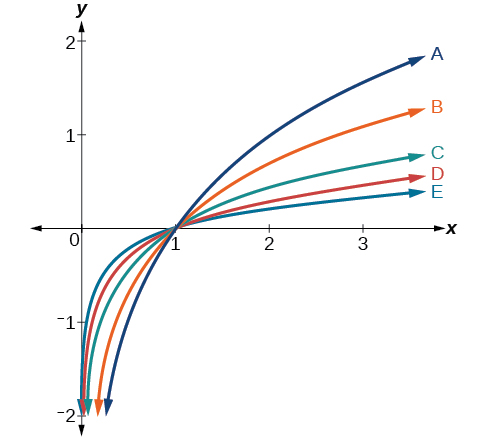
26)\(d(x)=\log (x)\)
27)\(f(x)=\ln (x)\)
- Resposta
-
\(B\)
28)\(g(x)=\log_2 (x)\)
29)\(h(x)=\log_5 (x)\)
- Resposta
-
\(C\)
30)\(j(x)=\log_{25} (x)\)
Para os exercícios a seguir, combine cada função na Figura com a letra correspondente ao seu gráfico.
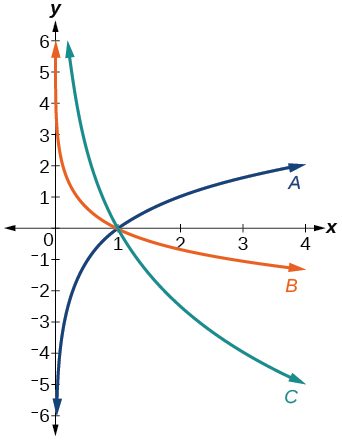
31)\(f(x)=\log_{\frac{1}{3}} (x)\)
- Resposta
-
\(B\)
32)\(g(x)=\log_2 (x)\)
33)\(h(x)=\log_{\frac{3}{4}} (x)\)
- Resposta
-
\(C\)
Para os exercícios a seguir, esboce os gráficos de cada par de funções no mesmo eixo.
34)\(f(x)=\log (x)\) e\(g(x)=10^x\)
35)\(f(x)=e^x\) e\(g(x)=\ln (x)\)
- Resposta
-
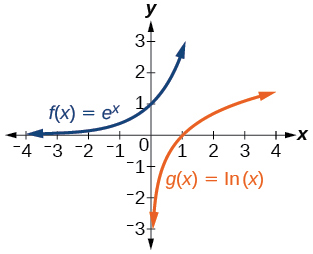
Para os exercícios a seguir, combine cada função na Figura com a letra correspondente ao seu gráfico.
36)\(f(x)=\log _4(-x+2)\)
37)\(g(x)=-\log _4(x+2)\)
- Resposta
-
\(C\)
38)\(h(x)=\log _4(x+2)\)
Para os exercícios a seguir, esboce o gráfico da função indicada.
39)\(f(x)=\log _2(x+2)\)
- Resposta
-
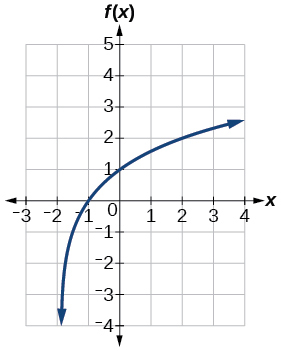
40)\(f(x)=2\log (x)\)
41)\(f(x)=\ln (-x)\)
- Resposta
-
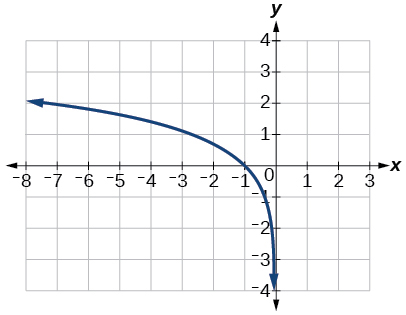
(42)\(g(x)=\log (4x+16)+4\)
43)\(g(x)=\log (6-3x)+1\)
- Resposta
-
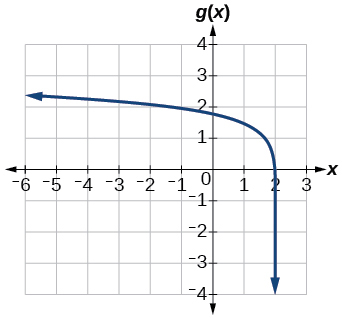
44)\(h(x)=-\dfrac{1}{2}\log (x+1)-3\)
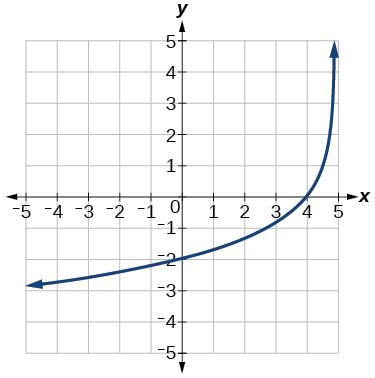
Para os exercícios a seguir, escreva uma equação logarítmica correspondente ao gráfico mostrado.
45) Uso\(y=\log _2(x)\)

- Resposta
-
\(f(x)=\log _2(-(x-1))\)
46) Use\(f(x)=\log _3(x)\) como função principal.
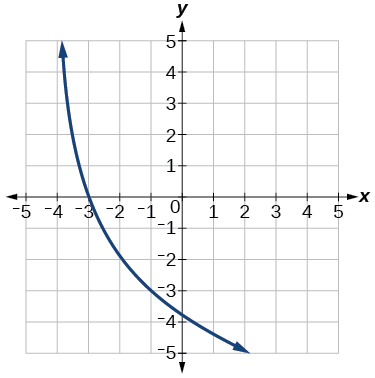
47) Use\(f(x)=\log _4(x)\) como função principal.
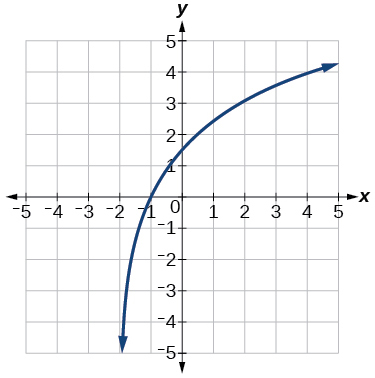
- Resposta
-
\(f(x)=3\log _4(x+2)\)
48) Use\(f(x)=\log _5(x)\) como função principal.
Tecnologia
Para os exercícios a seguir, use uma calculadora gráfica para encontrar soluções aproximadas para cada equação.
49)\(\log (x-1)+2=\ln (x-1)+2\)
- Resposta
-
\(x=2\)
50)\(\log (2x-3)+2=-\log (2x-3)+5\)
51)\(\ln (x-2)+2=-\ln (x+1)\)
- Resposta
-
\(x\approx 2.303\)
52)\(2\ln (5x+1)=\dfrac{1}{2}\ln (-5x)+1\)
53)\(\dfrac{1}{3}\log (1-x)=\log (x+1)+\dfrac{1}{3}\)
- Resposta
-
\(x\approx -0.472\)
Extensões
54)\(b\) Seja qualquer número real positivo tal que\(b\neq 1\)
55) Explore e discuta os gráficos de\(f(x)=\log_{\frac{1}{2}}(x)\) e\(g(x)=-\log _2(x)\)
- Responda
-
Os gráficos de\(f(x)=\log_{\frac{1}{2}}(x)\) e\(g(x)=-\log _2(x)\) parecem ser os mesmos;
Conjectura: para qualquer base positiva\(b\neq 1\),\(\log_{b}(x)=\log_{\frac{1}{b}}(x)\)
56) Prove a conjectura feita no exercício anterior.
57) Qual é o domínio da função\(f(x)=\ln \left (\frac{x+2}{x-4} \right )\)
- Responda
-
Lembre-se de que o argumento de uma função logarítmica deve ser positivo, então determinamos onde\(\frac{x+2}{x-4}> 0\). Do gráfico da função\(f(x)=\frac{x+2}{x-4}\)
, . . 
58) Use as propriedades dos expoentes para encontrar os\(x\) interceptos -da função\(f(x)=\log \left ( x^2+4x+4 \right )\) algebricamente. Mostre as etapas para resolver e, em seguida, verifique o resultado representando graficamente a função.
4.5: Propriedades logarítmicas
Lembre-se de que as funções logarítmica e exponencial “se desfazem”. Isso significa que os logaritmos têm propriedades semelhantes aos expoentes. Algumas propriedades importantes dos logaritmos são dadas aqui.
Verbal
1) Como a regra de potência para logaritmos ajuda na resolução de logaritmos com o formulário\(\log _b(\sqrt[n]{x})\)
- Responda
-
Qualquer expressão raiz pode ser reescrita como uma expressão com um expoente racional para que a regra de potência possa ser aplicada, facilitando o cálculo do logaritmo. Assim,\(\log _b \left ( x^{\frac{1}{n}} \right ) = \dfrac{1}{n}\log_{b}(x)\).
2) O que a fórmula de mudança de base faz? Por que é útil ao usar uma calculadora?
Algébrico
Para os exercícios a seguir, expanda cada logaritmo o máximo possível. Reescreva cada expressão como uma soma, diferença ou produto de registros.
3)\(\log _b (7x\cdot 2y)\)
- Responda
-
\(\log _b (2)+\log _b (7)+\log _b (x)+\log _b (y)\)
4)\(\ln (3ab\cdot 5c)\)
5)\(\log_b \left ( \dfrac{13}{17} \right )\)
- Responda
-
\(\log _b (13)-\log _b (17)\)
6)\(\log_4 \left ( \dfrac{\frac{x}{z}}{w} \right )\)
7)\(\ln \left ( \dfrac{1}{4^k} \right )\)
- Responda
-
\(-k\ln(4)\)
8)\(\log _2 (y^x)\)
Para os exercícios a seguir, condense em um único logaritmo, se possível.
9)\(\ln (7)+\ln (x)+\ln (y)\)
- Responda
-
\(\ln(7xy)\)
10)\(\log_3(2)+\log_3(a)+\log_3(11)+\log_3(b)\)
11)\(\log_b(28)-\log_b(7)\)
- Responda
-
\(\log_b(4)\)
12)\(\ln (a)-\ln (d)-\ln (c)\)
13)\(-\log_b\left ( \dfrac{1}{7} \right )\)
- Responda
-
\(\log_b(7)\)
14)\(\dfrac{1}{3}\ln(8)\)
Para os exercícios a seguir, use as propriedades dos logaritmos para expandir cada logaritmo o máximo possível. Reescreva cada expressão como uma soma, diferença ou produto de registros.
15)\(\log \left ( \dfrac{x^{15}y^{13}}{z^{19}} \right )\)
- Responda
-
\(15\log (x)+13\log (y)-19\log (z)\)
16)\(\ln \left ( \frac{a^{-2}}{b^{-4}c^{5}} \right )\)
17)\(\log \left ( \sqrt{x^3y^{-4}} \right )\)
- Responda
-
\(\frac{3}{2}\log (x)-2\log (y)\)
18)\(\ln \left ( y\sqrt{\frac{y}{1-y}} \right )\)
19)\(\log \left ( x^2y^3 \sqrt[3]{x^2y^5} \right )\)
- Responda
-
\(\dfrac{8}{3}\log (x)+\dfrac{14}{3}\log (y)\)
Para os exercícios a seguir, condense cada expressão em um único logaritmo usando as propriedades dos logaritmos.
20)\(\log \left ( 2x^4 \right )+\log \left (3x^5 \right )\)
21)\(\ln \left ( 6x^9 \right )-\ln \left (3x^2 \right )\)
- Responda
-
\(\ln \left ( 2x^7 \right )\)
22)\(2\log (x)+3\log (x+1)\)
23)\(\log (x)-\dfrac{1}{2}\log (y)+3\log (z)\)
- Responda
-
\(\log \left ( \dfrac{xz^3}{\sqrt{y}} \right )\)
24)\(4\log _7(c)+\dfrac{\log _7(a)}{3}+\dfrac{\log _7(b)}{3}\)
Para os exercícios a seguir, reescreva cada expressão como uma proporção equivalente de registros usando a base indicada.
25)\(\log _7(15)\) para a base\(e\)
- Responda
-
\(\log _7(15)=\dfrac{\ln (15)}{\ln (7)}\)
Para os exercícios a seguir, suponha\(\log _5(6)=a\) e\(\log _5(11)=b\)
27)\(\log _{11} (5)\)
- Responda
-
\(\log _{11} (5)=\dfrac{\log_5 (5)}{\log_5 (11)}=\dfrac{1}{b}\)
28)\(\log _{6} (55)\)
29)\(\log _{11}\left (\dfrac{6}{11} \right )\)
- Responda
-
\(\log _{11}\left (\dfrac{6}{11} \right )=\dfrac{\log _{11}\left (\frac{6}{11} \right )}{\log _{5}(11)}=\dfrac{\log _{5}(6)-\log _{5}(11)}{\log _{5}(11)}=\dfrac{a-b}{b}=\dfrac{a}{b}-1\)
Numérico
Para os exercícios a seguir, use as propriedades dos logaritmos para avaliar sem usar uma calculadora.
30)\(\log _3 \left ( \dfrac{1}{9} \right )-3\log _3 (3)\)
31)\(6\log _8 (2)+\dfrac{\log _8 (64)}{3\log _8 (4)}\)
- Responda
-
\(3\)
32)\(2\log _9 (3)-4\log _9 (3)+\log _9 \left (\dfrac{1}{729} \right )\)
Para os exercícios a seguir, use a fórmula de mudança de base para avaliar cada expressão como um quociente de registros naturais. Use uma calculadora para aproximar cada uma delas a cinco casas decimais.
33)\(\log _3 (22)\)
- Responda
-
\(2.81359\)
34)\(\log _8 (65)\)
(35)\(\log _6 (5.38)\)
- Responda
-
\(0.93913\)
36)\(\log _4 \left (\dfrac{15}{2} \right )\)
37)\(\log _{\frac{1}{2}} (4.7)\)
- Responda
-
\(-2.23266\)
Extensões
38) Use a regra do produto para logaritmos para encontrar todos os\(x\) valores, de forma que\(\log _{12} (2x+6)+\log _{12} (x+2)=2\)
39) Use a regra do quociente para logaritmos para encontrar todos os\(x\) valores de forma que\(\log _{6} (x+2)-\log _{6} (x-3)=1\)
- Responda
-
Reescrevendo como uma equação exponencial e resolvendo\(x\):
\ (\ begin {align*}
6^1 &=\ frac {x+2} {x-3}\\
0 &=\ frac {x+2} {x-3} -6\\
0 &=\ frac {x+2} {x-3} -\ frac {6 (x-3)} {(x-3)}\\
0 &=\ frac {x+2-6x+18} {x-3}\\
0 &=\ frac {x-4} {x-3}\\
x &= 4
\ end {align*}\)Verificando, descobrimos que\(\log _6(4+2)-\log _6(4-3)=\log _6(6)-\log _6(1)\) está definido, então\(x=4\)
40) A propriedade de potência dos logaritmos pode ser derivada da propriedade de potência dos expoentes usando a equação\(b^x=m\)
41) Prove isso\(\log_b(n)=\frac{1}{\log_b(n)}\) para quaisquer números inteiros positivos\(b>1\) e\(n>1\)
- Responda
-
Seja\(b\) e\(n\) seja números inteiros positivos maiores que\(1\)
.
42) Faz\(\log_{81}(2401)=\log_3(7)\)
4.6: Equações exponenciais e logarítmicas
O crescimento populacional descontrolado pode ser modelado com funções exponenciais. As equações resultantes dessas funções exponenciais podem ser resolvidas para analisar e fazer previsões sobre o crescimento exponencial. Nesta seção, aprenderemos técnicas para resolver funções exponenciais.
Verbal
1) Como uma equação exponencial pode ser resolvida?
- Responda
-
Determine primeiro se a equação pode ser reescrita para que cada lado use a mesma base. Nesse caso, os expoentes podem ser definidos como iguais entre si. Se a equação não puder ser reescrita para que cada lado use a mesma base, aplique o logaritmo em cada lado e use as propriedades dos logaritmos para resolver.
2) Quando ocorre uma solução estranha? Como uma solução externa pode ser reconhecida?
3) Quando a propriedade um-para-um dos logaritmos pode ser usada para resolver uma equação? Quando não pode ser usado?
- Responda
-
A propriedade um-para-um pode ser usada se os dois lados da equação puderem ser reescritos como um único logaritmo com a mesma base. Nesse caso, os argumentos podem ser iguais entre si e a equação resultante pode ser resolvida algebricamente. A propriedade um-para-um não pode ser usada quando cada lado da equação não pode ser reescrito como um único logaritmo com a mesma base.
Algébrico
Para os exercícios a seguir, use bases semelhantes para resolver a equação exponencial.
4)\(4^{-3v-2}=4^{-v}\)
5)\(64\cdot 4^{3x}=16\)
- Responda
-
\(x=-\dfrac{1}{3}\)
6)\(3^{2x+1}\cdot 3^x=243\)
7)\(2^{-3n}\cdot \dfrac{1}{4}=2^{n+2}\)
- Responda
-
\(n=-1\)
8)\(625\cdot 5^{3x+3}=125\)
9)\(\frac{36^{3b}}{36^{2b}}=216^{2-b}\)
- Responda
-
\(b=\dfrac{6}{5}\)
10)\(\left (\dfrac{1}{64} \right )^{3n}\cdot 8=2^6\)
Para os exercícios a seguir, use logaritmos para resolver.
11)\(9^{x-10}=1\)
- Responda
-
\(x=10\)
12)\(2e^{6x}=13\)
13)\(e^{r+10}-10=-42\)
- Responda
-
Sem solução
14)\(2\cdot 10^{9a}=29\)
15)\(-8\cdot 10^{p+7}-7=-24\)
- Responda
-
\(p=\log \left (\frac{17}{8} \right )-7\)
16)\(7e^{3n-5}+5=-89\)
17)\(e^{-3k}+6=44\)
- Responda
-
\(k=-\frac{\ln(38)}{3}\)
18)\(-5e^{9x-8}-8=-62\)
19)\(-6e^{9x+8}+2=-74\)
- Responda
-
\(x=\frac{\frac{\ln(38)}{3}-8}{9}\)
20)\(2^{x+1}=5^{2x-1}\)
21)\(e^{2x}-e^{x}-132=0\)
- Responda
-
\(x=\ln 12\)
22)\(7e^{8x+8}-5=-95\)
23)\(10e^{8x+3}+2=8\)
- Responda
-
\(x=\frac{\frac{\ln(3)}{5}-3}{8}\)
24)\(4e^{3x+3}-7=53\)
25)\(8e^{-5x-2}-4=-90\)
- Responda
-
Sem solução
26)\(3^{2x+1}=7^{x-2}\)
27)\(e^{2x}-e^{x}-6=0\)
- Responda
-
\(x=\ln 3\)
28)\(3e^{3-3x}+6=-31\)
Para os exercícios a seguir, use a definição de um logaritmo para reescrever a equação como uma equação exponencial.
29)\(\log \left ( \frac{1}{100} \right )=-2\)
- Responda
-
\(10^{-2}=\dfrac{1}{100}\)
30)\(\log _{324}(18)=\dfrac{1}{2}\)
Para os exercícios a seguir, use a definição de um logaritmo para resolver a equação.
31)\(5\log _{7}n=10\)
- Responda
-
\(n=49\)
32)\(-8\log _{9}x=16\)
33)\(4+\log _{2}(9k)=2\)
- Responda
-
\(k=\dfrac{1}{36}\)
34)\(2\log (8n+4)+6=10\)
(35)\(10-4\ln (9-8x)=6\)
- Responda
-
\(x=\dfrac{9-e}{8}\)
Para os exercícios a seguir, use a propriedade um-para-um dos logaritmos para resolver.
36)\(\ln (10-3x)=\ln (-4x)\)
37)\(\log_{13} (5n-2)=\log_{13} (8-5n)\)
- Responda
-
\(n=1\)
38)\(\log (x+3)-\log (x)=\log (74)\)
39)\(\ln (-3x)=\ln (x^2-6x)\)
- Responda
-
Sem solução
40)\(\log_4 (6-m)=\log_4 (3m)\)
41)\(\ln (x-2)-\ln (x)=\ln (54)\)
- Responda
-
Sem solução
42)\(\log_9 (2n^2-14n)=\log_9 (-45+n^2)\)
43)\(\ln (x^2-10)+\ln (9)=\ln (10)\)
- Responda
-
\(x=\pm \frac{10}{3}\)
Para os exercícios a seguir, resolva cada equação para\(x\).
44)\(\log (x+12)=\log (x)+\log (12)\)
45)\(\ln (x)+\ln (x-3)=\ln (7x)\)
- Responda
-
\(x=10\)
46)\(\log_2 (7x+6)=3\)
47)\(\ln (7)+\ln (2-4x^2)=\ln (14)\)
- Responda
-
\(x=0\)
48)\(\log_8 (x+6)-\log_8 (x)=\log_8 (58)\)
49)\(\ln (3)-\ln (3-3x)=\ln (4)\)
- Responda
-
\(x=\dfrac{3}{4}\)
50)\(\log_3 (3x)-\log_3 (6)=\log_3 (77)\)
Gráfica
Para os exercícios a seguir, resolva a equação para\(x\)
51)\(\log_9 (x)-5=-4\)
- Responda
-
\(x=9\)
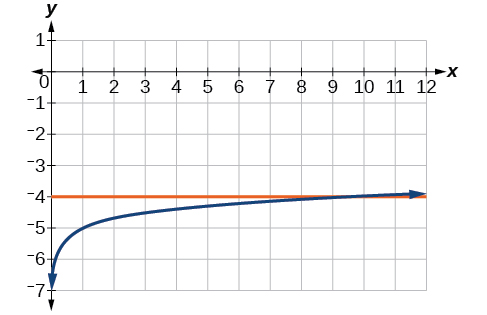
52)\(\log_3 (x)+3=2\)
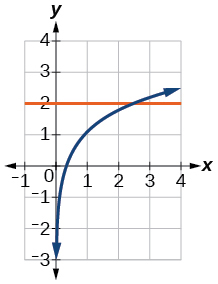
53)\(\ln (3x)=2\)
- Responda
-
\(x=\dfrac{e^2}{3}\approx 2.5\)
54)\(\ln (x-5)=1\)
55)\(\log (4)+\log (-5x)=2\)
- Responda
-
\(x=-5\)
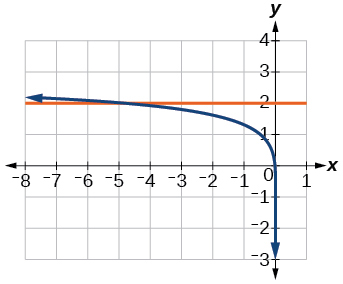
56)\(-7+\log_3 (4-x)=-6\)
57)\(\ln (4x-10)-6=-5\)
- Responda
-
\(x=\dfrac{e+10}{4}\approx 3.2\)
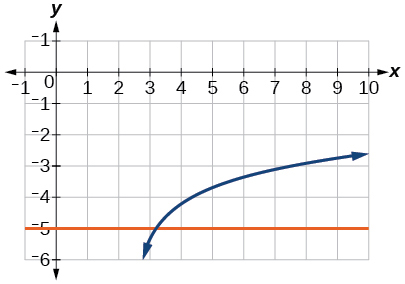
58)\(\log (4-2x)=\log (-4x)\)
59)\(\log_{11} (-2x^2 -7x)=\log_{11} (x-2)\)
- Responda
-
Sem solução
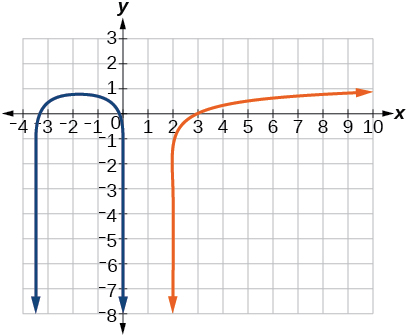
60)\(\ln (2x+9)=\ln (-5x)\)
61)\(\log_9 (3-x)=\log_9 (4x-8)\)
- Responda
-
\(x=\dfrac{11}{5}\approx 2.2\)
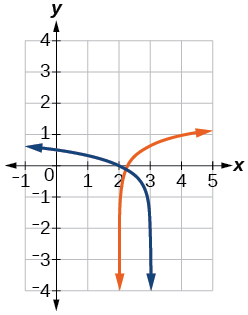
62)\(\log (x^2+13)=\log (7x+3)\)
63)\(\dfrac{3}{\log _2(10)}-\log (x-9)=\log (44)\)
- Responda
-
\(x=\dfrac{101}{11}\approx 9.2\)
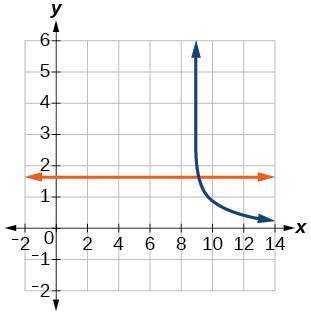
64)\(\ln (x)-\ln (x+3)=\ln (6)\)
Para os exercícios a seguir, resolva o valor indicado e represente graficamente a situação mostrando o ponto de solução.
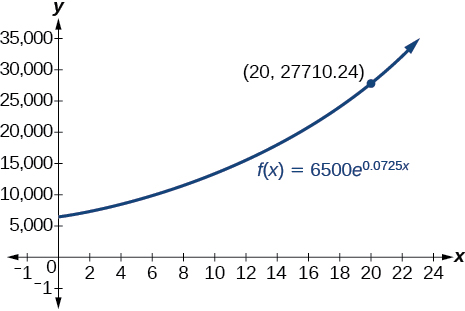
65) Uma conta com um depósito\(\$6,500\) inicial de juros\(7.25\%\) anuais, compostos continuamente. Quanto valerá a conta depois de\(20\) anos?
- Responda
-
sobre\(\$27,710.24\)
66) A fórmula para medir a intensidade do som em decibéis\(D\) é definida pela equação\(D=10\log \left ( \frac{I}{I_0} \right )\)
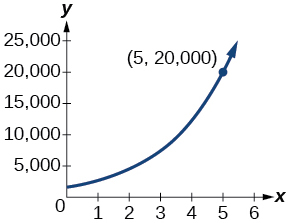
67) A população de uma cidade pequena é modelada pela equação em\(P=1650e^{0.5t}\) que\(t\) é medida em anos. Em aproximadamente quantos anos a população da cidade chegará\(20,000\)?
- Responda
-
cerca de\(5\) anos
Tecnologia
Para os exercícios a seguir, resolva cada equação reescrevendo a expressão exponencial usando o logaritmo indicado. Em seguida, use uma calculadora para aproximar a variável às\(3\) casas decimais.
68)\(1000(1.03)^t=5000\) usando o registro comum.
69)\(e^{5x}=17\) usando o tronco natural.
- Responda
-
\(\dfrac{\ln (17)}{5}\approx 0.567\)
70)\(3(1.04)^{3t}=8\) usando o registro comum
71)\(3^{4x-5}=38\) usando o registro comum
- Responda
-
\(x=\dfrac{\log (38+5\log (3))}{4\log(3)}\approx 2.078\)
72)\(50e^{-0.12t}=10\) usando o tronco natural
Para os exercícios a seguir, use uma calculadora para resolver a equação. Salvo indicação em contrário, arredonde todas as respostas para o décimo milésimo mais próximo.
73)\(7e^{3x-5}+7.9=47\)
- Responda
-
\(x\approx 2.2401\)
74)\(\ln (3)+\ln (4.4x+6.8)=2\)
75)\(\log(-0.7x-9)=1+5\log(5)\)
- Responda
-
\(x\approx -44655.7143\)
76) A pressão atmosférica\(P\) em libras por polegada quadrada é representada pela fórmula\(P=14.7e^{-0.21x}\)
77) A magnitude\(M\) de um terremoto é representada pela equação\(M=\dfrac{2}{3}\log \left ( \dfrac{E}{E_0} \right )\) onde\(E\) é a quantidade de energia liberada pelo terremoto em joules\(E_0=10^{4.4}\) e é a medida mínima atribuída liberada por um terremoto. Até o centésimo mais próximo, qual seria a magnitude de um terremoto liberando\(1.4\cdot 10^{13}\) joules de energia?
- Responda
-
sobre\(5.83\)
Extensões
78) Use a definição de um logaritmo junto com a propriedade um-para-um dos logaritmos para provar isso\(b^{\log_b x}=x\).
79) Lembre-se da fórmula para aumentar continuamente os juros,\(y=Ae^{kt}\)
- Resposta
-
\(t=\ln \left ( \left ( \dfrac{y}{A} \right )^{\frac{1}{k}} \right )\)
80) Lembre-se da fórmula de juros compostos\(A=a\left ( 1+\frac{r}{k} \right )^{kt}\)
81) A Lei do Resfriamento de Newton afirma que a temperatura\(T\) de um objeto a qualquer momento\(t\) pode ser descrita pela equação\(T=T_s+(T_0-T_s)e^{-kt}\)
- Resposta
-
\(t=\ln \left ( \left ( \frac{T-T_s}{T_0-T_s} \right )^{-\frac{1}{k}} \right )\)
4.7: Modelos exponenciais e logarítmicos
Já exploramos algumas aplicações básicas de funções exponenciais e logarítmicas. Nesta seção, exploramos algumas aplicações importantes com mais profundidade, incluindo isótopos radioativos e a Lei do Resfriamento de Newton.
Verbal
1) Com que tipo de modelo exponencial a meia-vida estaria associada? Qual o papel da meia-vida nesses modelos?
- Resposta
-
A meia-vida é uma medida de decaimento e, portanto, está associada a modelos de decaimento exponencial. A meia-vida de uma substância ou quantidade é a quantidade de tempo que leva para que metade da quantidade inicial dessa substância ou quantidade se decomponha.
2) O que é datação por carbono? Por que isso funciona? Dê um exemplo em que a datação por carbono seria útil.
3) Com que tipo de modelo exponencial o tempo de duplicação estaria associado? Qual o papel da duplicação do tempo nesses modelos?
- Resposta
-
O tempo de duplicação é uma medida do crescimento e, portanto, está associado a modelos de crescimento exponencial. O tempo de duplicação de uma substância ou quantidade é a quantidade de tempo necessária para que a quantidade inicial dessa substância ou quantidade dobre de tamanho.
4) Defina a Lei do Resfriamento de Newton. Em seguida, cite pelo menos três situações do mundo real em que a Lei do Resfriamento de Newton seria aplicada.
5) O que é uma ordem de grandeza? Por que ordens de magnitude são úteis? Dê um exemplo para explicar.
- Resposta
-
Uma ordem de magnitude é a potência mais próxima de dez pela qual uma quantidade cresce exponencialmente. Também é uma posição aproximada em uma escala logarítmica; Resposta da amostra: Ordens de magnitude são úteis para fazer comparações entre números que diferem em grande quantidade. Por exemplo, a massa de Saturno é\(95\) vezes maior que a massa da Terra. Isso é o mesmo que dizer que a massa de Saturno é cerca de\(10^2\) vezes, ou\(2\) ordens de magnitude maior, do que a massa da Terra.
Numérico
6) A temperatura de um objeto em graus Fahrenheit após\(t\) minutos é representada pela equação\(T(t)=68e^{-0.0174t}+72\)
Para os exercícios a seguir, use o modelo de crescimento logístico \(f(x)=\dfrac{150}{1+8e^{-2x}}\)
7) Encontre e interprete\(f(0)\)
- Resposta
-
\(f(0)\approx 16.7\); A quantidade inicialmente presente é de cerca de\(16.7\) unidades.
8) Encontre e interprete\(f(4)\)
9) Encontre a capacidade de carga.
- Resposta
-
\(150\)
10) Representar graficamente o modelo.
11) Determine se os dados da tabela poderiam ser melhor representados como uma função linear, exponencial ou logarítmica. Em seguida, escreva uma fórmula para um modelo que represente os dados.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">—2 | \ (f (x)\) ">0,694 |
| \ (x\) ">—1 | \ (f (x)\) ">0,833 |
| \ (x\) ">0 | \ (f (x)\) ">1 |
| \ (x\) ">1 | \ (f (x)\) ">1,2 |
| \ (x\) ">2 | \ (f (x)\) ">1,44 |
| \ (x\) ">3 | \ (f (x)\) ">1,728 |
| \ (x\) ">4 | \ (f (x)\) ">2,074 |
| \ (x\) ">5 | \ (f (x)\) ">2,488 |
- Resposta
-
exponencial;\(f(x)=1.2^x\)
12) Reescreva\(f(x)=1.68(0.65)^x\) como uma equação exponencial com base\(e\) em cinco dígitos significativos.
Tecnologia
Para os exercícios a seguir, insira os dados de cada tabela em uma calculadora gráfica e represente graficamente os gráficos de dispersão resultantes. Determine se os dados da tabela podem representar uma função linear, exponencial ou logarítmica.
13)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">2 |
| \ (x\) ">2 | \ (f (x)\) ">4,079 |
| \ (x\) ">3 | \ (f (x)\) ">5.296 |
| \ (x\) ">4 | \ (f (x)\) ">6,159 |
| \ (x\) ">5 | \ (f (x)\) ">6.828 |
| \ (x\) ">6 | \ (f (x)\) ">7,375 |
| \ (x\) ">7 | \ (f (x)\) ">7.838 |
| \ (x\) ">8 | \ (f (x)\) ">8.238 |
| \ (x\) ">9 | \ (f (x)\) ">8.592 |
| \ (x\) ">10 | \ (f (x)\) ">8.908 |
- Resposta
-
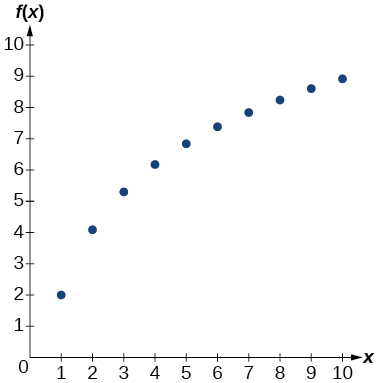
14)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">2,4 |
| \ (x\) ">2 | \ (f (x)\) ">2,88 |
| \ (x\) ">3 | \ (f (x)\) ">3.456 |
| \ (x\) ">4 | \ (f (x)\) ">4,147 |
| \ (x\) ">5 | \ (f (x)\) ">4,977 |
| \ (x\) ">6 | \ (f (x)\) ">5.972 |
| \ (x\) ">7 | \ (f (x)\) ">7,166 |
| \ (x\) ">8 | \ (f (x)\) ">8,6 |
| \ (x\) ">9 | \ (f (x)\) ">10,32 |
| \ (x\) ">10 | \ (f (x)\) ">12.383 |
15)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">4 | \ (f (x)\) ">9.429 |
| \ (x\) ">5 | \ (f (x)\) ">9.972 |
| \ (x\) ">6 | \ (f (x)\) ">10.415 |
| \ (x\) ">7 | \ (f (x)\) ">10,79 |
| \ (x\) ">8 | \ (f (x)\) ">11,115 |
| \ (x\) ">9 | \ (f (x)\) ">11.401 |
| \ (x\) ">10 | \ (f (x)\) ">11.657 |
| \ (x\) ">11 | \ (f (x)\) ">11,889 |
| \ (x\) ">12 | \ (f (x)\) ">12.101 |
| \ (x\) ">13 | \ (f (x)\) ">12.295 |
- Resposta
-
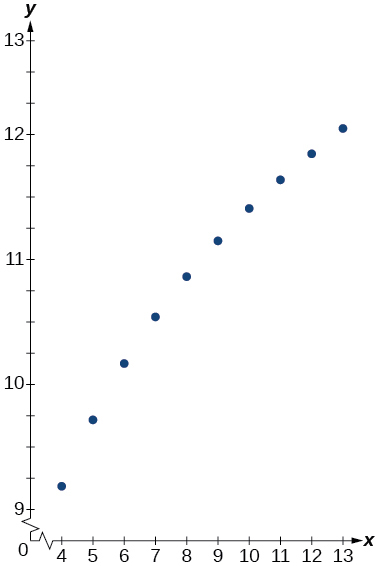
16)
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1,25 | \ (f (x)\) ">5,75 |
| \ (x\) ">2,25 | \ (f (x)\) ">8,75 |
| \ (x\) ">3,56 | \ (f (x)\) ">12,68 |
| \ (x\) ">4,2 | \ (f (x)\) ">14,6 |
| \ (x\) ">5,65 | \ (f (x)\) ">18,95 |
| \ (x\) ">6,75 | \ (f (x)\) ">22,25 |
| \ (x\) ">7,25 | \ (f (x)\) ">23,75 |
| \ (x\) ">8,6 | \ (f (x)\) ">27,8 |
| \ (x\) ">9,25 | \ (f (x)\) ">29,75 |
| \ (x\) ">10,5 | \ (f (x)\) ">33,5 |
Para os exercícios a seguir, use uma calculadora gráfica e este cenário: a população de uma fazenda de peixes em\(t\) anos é modelada pela equação\(P(t)=\dfrac{1000}{1+9e^{-0.6t}}\)
17) Representar graficamente a função.
- Resposta
-
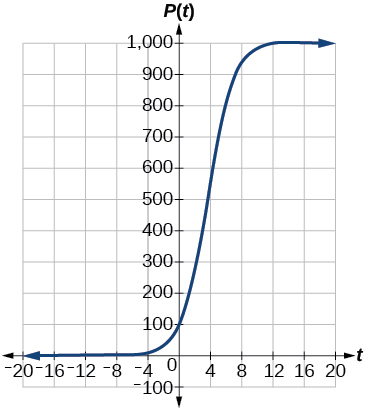
18) Qual é a população inicial de peixes?
19) Até o décimo mais próximo, qual é o tempo de duplicação para a população de peixes?
- Resposta
-
cerca de\(1.4\) anos
20) Para o número inteiro mais próximo, qual será a população de peixes depois de\(2\) anos?
21) Até o décimo mais próximo, quanto tempo a população levará para chegar\(900\)?
- Resposta
-
cerca de\(7.3\) anos
22) Qual é a capacidade de carga para a população de peixes? Justifique sua resposta usando o gráfico de\(P\).
Extensões
23) Uma substância tem meia-vida de\(2.045\) minutos. Se a quantidade inicial da substância fosse\(132.8\) gramas, quantas meias-vidas terão passado antes que a substância se decomponha em\(8.3\) gramas? Qual é o tempo total de decadência?
- Resposta
-
\(4\)meias-vidas;\(8.18\) minutos
24) A fórmula para uma população crescente é dada por\(P(t)=P_0e^{rt}\) onde\(P_0\) está a população inicial e\(r>0\)
25) Lembre-se da fórmula para calcular a magnitude de um terremoto,\(M=\dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )\)
- Resposta
-
\(\begin{align*} M&= \dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )\\ \log \left ( \dfrac{S}{S_0} \right )&= \dfrac{3}{2}M\\ \dfrac{S}{S_0}&= 10^{\frac{3M}{2}}\\ S&= S_0 10^{\frac{3M}{2}} \end{align*}\)
26) Qual é o\(y\) intercepto do modelo de crescimento logístico\(y=\dfrac{c}{1+ae^{-rx}}\)
27) Prove isso\(b^x=e^{x\ln (b)}\) de forma positiva\(b≠1\).
- Resposta
-
Deixe\(y=b^x\) um número real não negativo de\(b\) tal forma que\(b\neq1\)
. \(\begin{align*} \ln (y) &= \ln (b^x)\\ \ln (y) &= x\ln (b)\\ e^{\ln (y)} &= e^{x\ln (b)}\\ y&= e^{x\ln (b)} \end{align*}\)
Aplicativos do mundo real
Para os exercícios a seguir, use este cenário: um médico prescreve\(125\) miligramas de um medicamento terapêutico que se decompõe a\(30\%\) cada hora.
28) Até a hora mais próxima, qual é a meia-vida do medicamento?
29) Escreva um modelo exponencial representando a quantidade do medicamento restante no sistema do paciente após\(t\) horas. Em seguida, use a fórmula para encontrar a quantidade do medicamento que permaneceria no sistema do paciente após\(3\) horas. Arredonde para o miligrama mais próximo.
- Resposta
-
\(A=125e^{(-0.3567t)}\);\(A\approx 43\) mg
30) Usando o modelo encontrado no exercício anterior, encontre\(f(10\) e interprete o resultado. Arredonde para o centésimo mais próximo.
Para os exercícios a seguir, use este cenário: Um tumor é injetado com\(0.5\) gramas de iodo-125, que tem uma taxa de decaimento\(1.15\%\) por dia.
31) Até o dia mais próximo, quanto tempo levará para que metade do iodo-125 se decomponha?
- Resposta
-
cerca de\(60\) dias
32) Escreva um modelo exponencial representando a quantidade de iodo-125 restante no tumor após\(t\) dias. Em seguida, use a fórmula para encontrar a quantidade de iodo-125 que permaneceria no tumor após\(60\) dias. Arredonde para o décimo de grama mais próximo.
33) Um cientista começa com\(250\) gramas de uma substância radioativa. Depois de\(250\) minutos, a amostra caiu para\(32\) gramas. Arredondando para cinco dígitos significativos, escreva uma equação exponencial representando essa situação. Até o minuto mais próximo, qual é a meia-vida dessa substância?
- Resposta
-
\(f(t)=250e^{(-0.00914t)}\)
;
34) A meia-vida do Rádio-226 é de\(1590\) anos. Qual é a taxa de decaimento anual? Expresse o resultado decimal em quatro dígitos significativos e a porcentagem em dois dígitos significativos.
35) A meia-vida do Érbio-165 é de\(10.4\) horas. Qual é a taxa de decaimento por hora? Expresse o resultado decimal em quatro dígitos significativos e a porcentagem em dois dígitos significativos.
- Resposta
-
\(r\approx -0.0667\)
,
36) Um artefato de madeira de uma escavação arqueológica contém uma\(60\) porcentagem do carbono-14 presente nas árvores vivas. Até o ano mais próximo, quantos anos tem o artefato? (A meia-vida do carbono-14 é de\(5730\) anos.)
37) Um estudante de pesquisa está trabalhando com uma cultura de bactérias que dobra de tamanho a cada vinte minutos. A contagem inicial da população era de\(1350\) bactérias. Arredondando para cinco dígitos significativos, escreva uma equação exponencial representando essa situação. Para o número inteiro mais próximo, qual é o tamanho da população após o\(3\) expediente?
- Resposta
-
\(f(t)=1350e^{(0.03466t)}\); após o\(3\) expediente:\(P(180)\approx 691,200\)
Para os exercícios a seguir, use este cenário: Um biólogo registrou uma contagem de\(360\) bactérias presentes em uma cultura após\(5\) minutos e\(1000\) bactérias presentes após\(20\) minutos.
38) Para o número inteiro mais próximo, qual era a população inicial na cultura?
39) Arredondando para seis dígitos significativos, escreva uma equação exponencial representando essa situação. Até o minuto mais próximo, quanto tempo a população levou para dobrar?
- Resposta
-
\(f(t)=256e^{(0.068110t)}\); tempo de duplicação: cerca de\(10\) minutos
Para os exercícios a seguir, use este cenário: Uma panela de sopa fervente com temperatura interna de\(100^{\circ}\) Fahrenheit foi retirada do fogão para esfriar em uma sala\(69^{\circ}\) F. Depois de quinze minutos, a temperatura interna da sopa era\(95^{\circ}\) F.
40) Use a Lei do Resfriamento de Newton para escrever uma fórmula que modela essa situação.
41) Até o minuto mais próximo, quanto tempo a sopa levará para esfriar até\(80^{\circ}\) F?
- Resposta
-
cerca de\(88\) minutos
42) No grau mais próximo, qual será a temperatura após uma hora\(2\) e meia?
Para os exercícios a seguir, use este cenário: Um perú é retirado do forno com uma temperatura interna de\(165^{\circ}\) F e pode esfriar em uma sala\(75^{\circ}\) F. Depois de meia hora, a temperatura interna do perú é\(145^{\circ}\) F.
43) Escreva uma fórmula que modele essa situação.
- Resposta
-
\(T(t)=90e^{(-0.008377t)}+75\), onde\(t\) está em minutos.
44) No grau mais próximo, qual será a temperatura após\(50\) alguns minutos?
45) Até o minuto mais próximo, quanto tempo o perú levará para esfriar até\(110^{\circ}\) F?
- Resposta
-
cerca de\(113\) minutos
Para os exercícios a seguir, encontre o valor do número mostrado em cada escala logarítmica. Arredonde todas as respostas para o milésimo mais próximo.

- Resposta
-
\(\log(x)=1.5; x\approx 31.623\)
48) Faça um gráfico de cada conjunto de valores aproximados de intensidade dos sons em uma escala logarítmica: Sussurro:\(10^{-10}\dfrac{W}{m^2}\)
49) Lembre-se da fórmula para calcular a magnitude de um terremoto,\(M=\dfrac{2}{3}\log \left ( \dfrac{S}{S_0} \right )\)
- Resposta
-
Magnitude do MMS:\(5.82\)
Para os exercícios a seguir, use este cenário: A equação\(N(t)=\dfrac{500}{1+49e^{-0.7t}}\) modela o número de pessoas em uma cidade que ouviram um boato depois de\(t\) dias.
50) Quantas pessoas começaram o boato?
51) Até o número inteiro mais próximo, quantas pessoas terão ouvido o boato depois de\(3\) dias?
- Resposta
-
\(N(3)\approx 71\)
52) Peça a
Para o exercício a seguir, escolha a opção de resposta correta.
53) Um médico injeta em um paciente\(13\) miligramas de corante radioativo que se decompõe exponencialmente. Após\(12\) alguns minutos, restam\(4.75\) miligramas de corante no sistema do paciente. Qual é o modelo adequado para essa situação?
- \(f(t)=13(0.0805)^t\)
- \(f(t)=13e^{0.9195t}\)
- \(f(t)=13e^{(-0.0839t)}\)
- \(f(t)=\frac{4.75}{1+13e^{-0.83925t}}\)
- Resposta
-
c
4.8: Ajustando modelos exponenciais aos dados
Vamos nos concentrar em três tipos de modelos de regressão nesta seção: exponencial, logarítmico e logístico. Já ter trabalhado com cada uma dessas funções nos dá uma vantagem. Conhecer suas definições formais, o comportamento de seus gráficos e algumas de suas aplicações reais nos dá a oportunidade de aprofundar nosso entendimento. À medida que cada modelo de regressão é apresentado, as principais características e definições de sua função associada são incluídas para revisão.
Verbal
1) Quais situações são melhor modeladas por uma equação logística? Dê um exemplo e explique por que o exemplo é uma boa opção.
- Resposta
-
Os modelos logísticos são melhor usados para situações que têm valores limitados. Por exemplo, as populações não podem crescer indefinidamente, pois recursos como comida, água e espaço são limitados, então um modelo logístico descreve melhor as populações.
2) O que é uma capacidade de carga? Que tipo de modelo tem uma capacidade de carga embutida em sua fórmula? Por que isso faz sentido?
3) O que é análise de regressão? Descreva o processo de execução da análise de regressão em um utilitário gráfico.
- Resposta
-
A análise de regressão é o processo de encontrar uma equação que melhor se ajuste a um determinado conjunto de pontos de dados. Para realizar uma análise de regressão em um utilitário gráfico, primeiro liste os pontos fornecidos usando o menu STAT e depois EDIT. Em seguida, faça um gráfico do gráfico de dispersão usando o recurso STAT PLOT. A forma dos pontos de dados no gráfico de dispersão pode ajudar a determinar qual recurso de regressão usar. Depois que isso for determinado, selecione o comando de análise de regressão apropriado no menu STAT e depois CALC.
4) Qual seria a aparência de um gráfico de dispersão de pontos de dados se fosse melhor descrito por um modelo logarítmico?
5) A que corresponde o intercepto y no gráfico de uma equação logística para uma população modelada por essa equação?
- Resposta
-
O\(y\) intercepto -no gráfico de uma equação logística corresponde à população inicial do modelo populacional.
Gráfica
Para os exercícios a seguir, combine a função de melhor ajuste dada com o gráfico de dispersão apropriado na Figura (a) até a Figura (e). Responda usando a letra abaixo do gráfico correspondente.
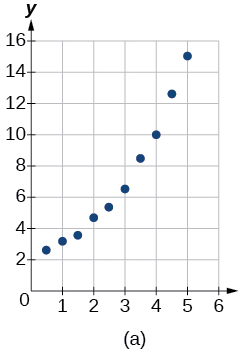
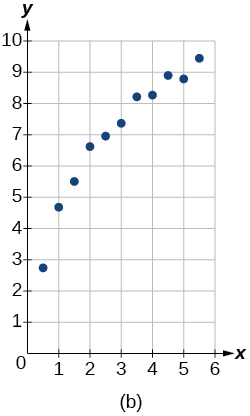
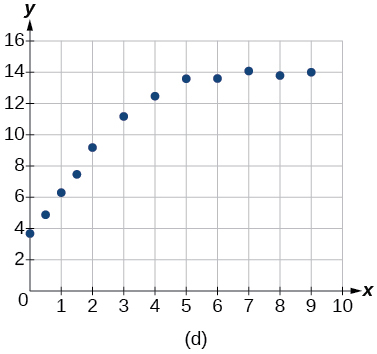
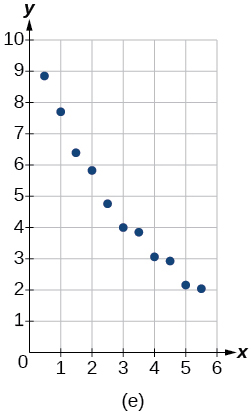
6)\(y=10.209e^{-0.294x}\)
7)\(y=5.598-1.912\ln (x)\)
- Resposta
-
c
8)\(y=2.104(1.479)^x\)
9)\(y=4.607+2.733\ln (x)\)
- Resposta
-
b
10)\(y=\dfrac{14.005}{1+2.79e^{-0.812x}}\)
Numérico
11) Para o número inteiro mais próximo, qual é o valor inicial de uma população modelada pela equação logística\(P(t)=\dfrac{175}{1+6.995e^{-0.68t}}\)
- Resposta
-
\(P(0)=22\);\(175\)
12) Reescreva o modelo exponencial\(A(t)=1550(1.085)^x\) como um modelo equivalente com base\(e\)
13) Um modelo logarítmico é dado pela equação\(h(p)=67.682-5.792\ln (p)\)
- Resposta
-
\(p\approx 2.67\)
14) Um modelo logístico é dado pela equação\(P(t)=\dfrac{90}{1+5e^{-0.42t}}\)
15) Qual é o\(y\) intercepto -no gráfico do modelo logístico dado no exercício anterior?
- Resposta
-
\(y\)-interceptar:\((0,15)\)
Tecnologia
Para os exercícios a seguir, use este cenário: A população\(P\) de um lago de carpas ao longo de\(x\) meses é modelada pela função\(P(x)=\dfrac{68}{1+16e^{-0.28x}}\).
16) Representar graficamente o modelo populacional para mostrar a população ao longo de um período de\(3\) anos.
17) Qual foi a população inicial de carpas?
- Resposta
-
\ (4)\ koi
18) Quantos carpas o lago terá após um ano e meio?
19) Quantos meses serão necessários até que haja\(20\) carpas na lagoa?
- Resposta
-
cerca de\(6.8\) meses
20) Use o recurso de interseção para aproximar o número de meses necessários até que a população da lagoa atinja a metade de sua capacidade de carga.
- Resposta
-
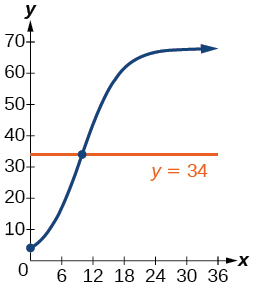
Para os exercícios a seguir, use este cenário: A população\(P\) de um habitat de espécies ameaçadas de extinção para lobos é modelada pela função\(P(x)=\dfrac{558}{1+54.8e^{-0.462x}}\)
21) Representar graficamente o modelo populacional para mostrar a população ao longo de um período de\(10\) anos.
22) Qual foi a população inicial de lobos transportada para o habitat?
- Resposta
-
\ (10)\ lobos
23) Quantos lobos o habitat terá depois de\(3\) anos?
24) Quantos anos serão necessários até que haja\(100\) lobos no habitat?
- Resposta
-
cerca de\(5.4\) anos
25) Use o recurso de interseção para aproximar o número de anos necessários até que a população do habitat atinja a metade de sua capacidade de carga.
Para os exercícios a seguir, consulte a Tabela abaixo.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">1125 |
| \ (x\) ">2 | \ (f (x)\) ">1495 |
| \ (x\) ">3 | \ (f (x)\) ">2310 |
| \ (x\) ">4 | \ (f (x)\) ">3294 |
| \ (x\) ">5 | \ (f (x)\) ">4650 |
| \ (x\) ">6 | \ (f (x)\) ">6361 |
26) Use uma calculadora gráfica para criar um diagrama de dispersão dos dados.
- Resposta
-
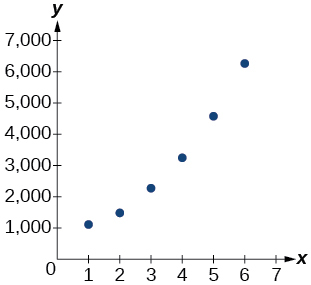
27) Use o recurso de regressão para encontrar uma função exponencial que melhor se ajuste aos dados na tabela.
28) Escreva a função exponencial como uma equação exponencial com base\(e\)
- Resposta
-
\(f(x)=776.682e^{0.3549x}\)
29) Representar graficamente a equação exponencial no diagrama de dispersão.
30) Use o recurso de interseção para encontrar o valor de\(x\) para qual\(f(x)=4000\).
- Resposta
-
Quando\(f(x)=4000\),\(x\approx 4.6\)
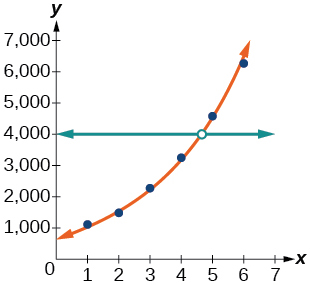
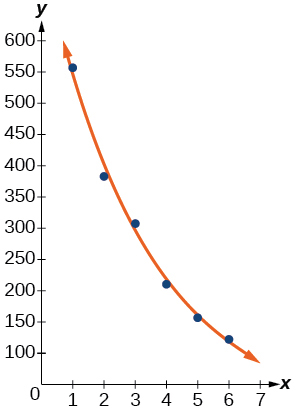
Para os exercícios a seguir, consulte a Tabela abaixo.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">555 |
| \ (x\) ">2 | \ (f (x)\) ">383 |
| \ (x\) ">3 | \ (f (x)\) ">307 |
| \ (x\) ">4 | \ (f (x)\) ">210 |
| \ (x\) ">5 | \ (f (x)\) ">158 |
| \ (x\) ">6 | \ (f (x)\) ">122 |
31) Use uma calculadora gráfica para criar um diagrama de dispersão dos dados.
32) Use o recurso de regressão para encontrar uma função exponencial que melhor se ajuste aos dados na tabela.
- Resposta
-
\(f(x)=731.92(0.738)^x\)
33) Escreva a função exponencial como uma equação exponencial com base\(e\)
34) Representar graficamente a equação exponencial no diagrama de dispersão.
- Resposta
-
35) Use o recurso de interseção para encontrar o valor de\(x\) para o qual\(f(x)=250\)
Para os exercícios a seguir, consulte a Tabela abaixo.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">5,1 |
| \ (x\) ">2 | \ (f (x)\) ">6,3 |
| \ (x\) ">3 | \ (f (x)\) ">7,3 |
| \ (x\) ">4 | \ (f (x)\) ">7,7 |
| \ (x\) ">5 | \ (f (x)\) ">8,1 |
| \ (x\) ">6 | \ (f (x)\) ">8,6 |
36) Use uma calculadora gráfica para criar um diagrama de dispersão dos dados.
- Resposta
-
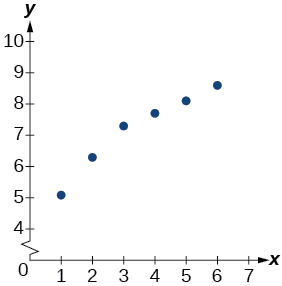
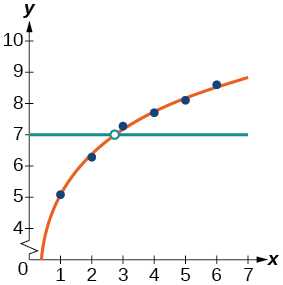
37) Use a opção Logaritmo do recurso Regression para encontrar uma função logarítmica do formulário\(y=a+b\ln (x)\) que melhor se ajuste aos dados na tabela.
38) Use a função logarítmica para encontrar o valor da função quando\(x=10\)
- Resposta
-
\(f(10)\approx 9.5\)
39) Representar graficamente a equação logarítmica no diagrama de dispersão.
40) Use o recurso de interseção para encontrar o valor de\(x\) para o qual\(f(x)=7\)
- Resposta
-
Quando\(f(x)=7\),\(x\approx 2.7\)
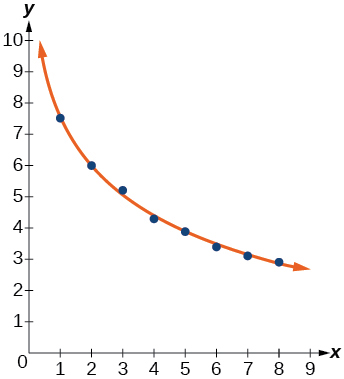
Para os exercícios a seguir, consulte a Tabela abaixo.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">7,5 |
| \ (x\) ">2 | \ (f (x)\) ">6 |
| \ (x\) ">3 | \ (f (x)\) ">5.2 |
| \ (x\) ">4 | \ (f (x)\) ">4,3 |
| \ (x\) ">5 | \ (f (x)\) ">3,9 |
| \ (x\) ">6 | \ (f (x)\) ">3,4 |
| \ (x\) ">7 | \ (f (x)\) ">3,1 |
| \ (x\) ">8 | \ (f (x)\) ">2,9 |
41) Use uma calculadora gráfica para criar um diagrama de dispersão dos dados.
42) Use a opção Logaritmo do recurso Regression para encontrar uma função logarítmica do formulário\(y=a+b\ln (x)\) que melhor se ajuste aos dados na tabela.
- Resposta
-
\(f(x)=7.544-2.268\ln (x)\)
43) Use a função logarítmica para encontrar o valor da função quando\(x=10\)
44) Representar graficamente a equação logarítmica no diagrama de dispersão.
- Resposta
-
45) Use o recurso de interseção para encontrar o valor de\(x\) para o qual\(f(x)=8\)
Para os exercícios a seguir, consulte a Tabela abaixo.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">1 | \ (f (x)\) ">8,7 |
| \ (x\) ">2 | \ (f (x)\) ">12,3 |
| \ (x\) ">3 | \ (f (x)\) ">15,4 |
| \ (x\) ">4 | \ (f (x)\) ">18,5 |
| \ (x\) ">5 | \ (f (x)\) ">20,7 |
| \ (x\) ">6 | \ (f (x)\) ">22,5 |
| \ (x\) ">7 | \ (f (x)\) ">23,3 |
| \ (x\) ">8 | \ (f (x)\) ">24 |
| \ (x\) ">9 | \ (f (x)\) ">24,6 |
| \ (x\) ">10 | \ (f (x)\) ">24,8 |
46) Use uma calculadora gráfica para criar um diagrama de dispersão dos dados.
- Resposta
-
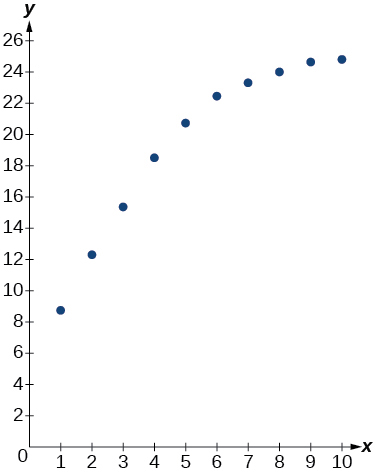
47) Use a opção de regressão LOGÍSTICA para encontrar um modelo de crescimento logístico do formulário\(y=\dfrac{c}{1+ae^{-bx}}\) que melhor se ajuste aos dados na tabela.
48) Representar graficamente a equação logística no diagrama de dispersão.
- Resposta
-
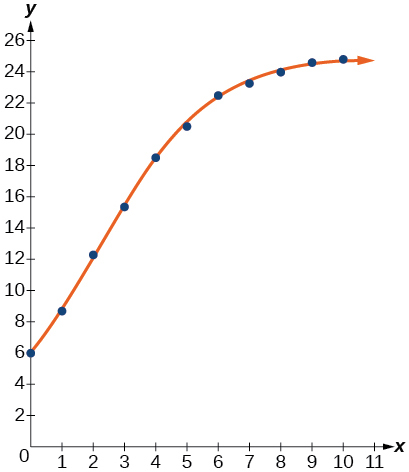
49) Para o número inteiro mais próximo, qual é a capacidade de carga prevista do modelo?
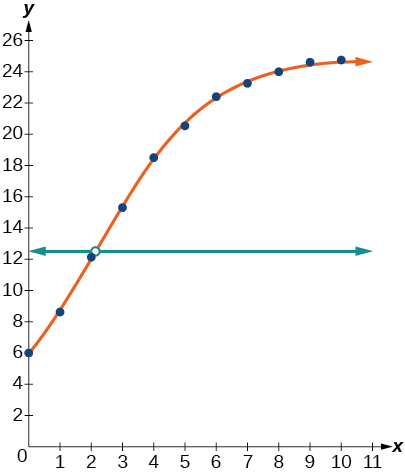
50) Use o recurso de interseção para encontrar o valor\(x\) pelo qual o modelo atinge metade de sua capacidade de carga.
- Resposta
-
Quando\(f(x)=12.5\),\(x\approx 2.1\)
Para os exercícios a seguir, consulte a Tabela abaixo.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">0 | \ (f (x)\) ">12 |
| \ (x\) ">2 | \ (f (x)\) ">28,6 |
| \ (x\) ">4 | \ (f (x)\) ">52,8 |
| \ (x\) ">5 | \ (f (x)\) ">70,3 |
| \ (x\) ">7 | \ (f (x)\) ">99,9 |
| \ (x\) ">8 | \ (f (x)\) ">112,5 |
| \ (x\) ">10 | \ (f (x)\) ">125,8 |
| \ (x\) ">11 | \ (f (x)\) ">127,9 |
| \ (x\) ">15 | \ (f (x)\) ">135,1 |
| \ (x\) ">17 | \ (f (x)\) ">135,9 |
51) Use uma calculadora gráfica para criar um diagrama de dispersão dos dados.
52) Use a opção de regressão LOGÍSTICA para encontrar um modelo de crescimento logístico do formulário\(y=\dfrac{c}{1+ae^{-bx}}\) que melhor se ajuste aos dados na tabela.
- Resposta
-
\(y=\dfrac{136.068}{1+10.324e^{-0.480x}}\)
53) Representar graficamente a equação logística no diagrama de dispersão.
54) Para o número inteiro mais próximo, qual é a capacidade de carga prevista do modelo?
- Resposta
-
sobre\(136\)
55) Use o recurso de interseção para encontrar o valor\(x\) pelo qual o modelo atinge metade de sua capacidade de carga.
Extensões
56) Lembre-se de que a forma geral de uma equação logística para uma população é dada por\(P(t)=\dfrac{c}{1+ae^{-bt}}\)
- Resposta
-
Trabalhando com o lado esquerdo da equação, vemos que ela pode ser reescrita como\(ae^{-bt}\)
: \ (\ begin {align*}
\ dfrac {c-p (t)} {P (t)} &=\ dfrac {c-\ frac {c} {1+ae^ {-bt}} {\ frac {c} {1+ae^ {-bt}}\\
&=\ dfrac {\ frac {c\ left (1+ae^ {-bt} direita) -c} {1+ae^ {-bt}} {\ frac {c} {1+ae^ {-bt}}}\\
&=\ dfrac {\ frac {c\ left (1+ae^ {-bt} -1\ direita)} {1+ae^ {-bt}}} {\ frac {c} {1+ae^ {-bt}}\\
&= 1+ae^ {-bt} -1\\
&= ae^ {-bt}
\ end {align*}\)\(\begin{align*} P_0 &= \dfrac{c}{1+ae^{-b(0)}}\\ &= \dfrac{c}{1+a} \end{align*}\)
Portanto,
\ (\ begin {align*}
\ dfrac {c-p_0} {P_0} e^ {-bt} &=\ dfrac {c-\ frac {c} {1+a}} {\ frac {c} {1+a}} e^ {-bt}\\
&=\ dfrac {\ frac {c (1+a) -c} {1+a}} {\ frac {c} {1+a}} e^ {-bt}\\
&=\ dfrac {\ frac {c (1+a -1)} {1+a}} {\ frac {c} {1+a}} e^ {-bt}\\
&= (1+a -1) e^ {-bt}\\
&= ae^ {-bt}
\ end {align*}\)Assim,
\(\dfrac{c-P(t)}{P(t)}=\dfrac{c-P_0}{P_0}e^{-bt}\)
57) Use um utilitário gráfico para encontrar uma fórmula de regressão exponencial\(f(x)\) e uma fórmula de regressão logarítmica\(g(x)\) para os pontos\((1.5,1.5)\) e\((8.5,8.5\)
58) Verifique a conjectura feita no exercício anterior. Arredonde todos os números para seis casas decimais quando necessário.
- Resposta
-
Primeiro, reescreva o exponencial com a base e:\(f(x)=1.034341e^{0.247800x}\)
. , \(\begin{align*} g(f(x)) &= 4.035510\ln\left (1.034341e^{0.247800x}\right )-0.136259\\ &= 4.03551(\ln \left(1.034341)+\ln\left (e^{0.2478x} \right)\right)-0.136259\\ &= 4.03551(\ln(1.034341)+0.2478x)-0.136259\\ &= 0.136257+0.999999x-0.136259\\ &= -0.000002+0.999999x\\ &\approx 0+x \\ &= x \end{align*}\)
59) Encontre a função inversa\(f^{-1}(x)\) para a função logística\(f(x)=\dfrac{c}{1+ae^{-bx}}\)
60) Use o resultado do exercício anterior para representar graficamente o modelo logístico\(P(t)=\dfrac{20}{1+4e^{-0.5t}}\)
- Resposta
-
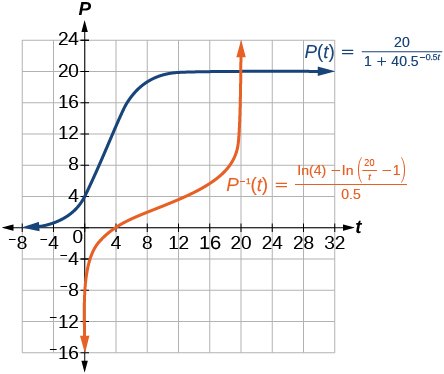
O gráfico de\(P(t)\) tem um\(y\) intercepto -em\((0, 4)\) e assíntotas horizontais em\(y = 0\)\(y = 20\) e. O gráfico de\(P^{-1}(t)\) tem um intercepto\(x\) - em\((4, 0)\) e assíntotas verticais em\(x = 0\)\(x = 20\) e.


