4.6: Equações exponenciais e logarítmicas
- Page ID
- 189211
- Use bases semelhantes para resolver equações exponenciais.
- Use logaritmos para resolver equações exponenciais.
- Use a definição de um logaritmo para resolver equações logarítmicas.
- Use a propriedade um-para-um dos logaritmos para resolver equações logarítmicas.
- Resolva problemas aplicados envolvendo equações exponenciais e logarítmicas.
Em 1859, um proprietário de terras australiano chamado Thomas Austin soltou\(24\) coelhos na natureza para caçar. Como a Austrália tinha poucos predadores e comida suficiente, a população de coelhos explodiu. Em menos de dez anos, a população de coelhos chegou aos milhões.

O crescimento populacional descontrolado, como nos coelhos selvagens na Austrália, pode ser modelado com funções exponenciais. As equações resultantes dessas funções exponenciais podem ser resolvidas para analisar e fazer previsões sobre o crescimento exponencial. Nesta seção, aprenderemos técnicas para resolver funções exponenciais.
Usando bases semelhantes para resolver equações exponenciais
A primeira técnica envolve duas funções com bases semelhantes. Lembre-se de que a propriedade um-para-um das funções exponenciais nos diz que, para qualquer número real\(b\)\(S\)\(T\), e\(b>0\), onde\(b≠1\),\(b^S=b^T\) se e somente se\(S=T\).
Em outras palavras, quando uma equação exponencial tem a mesma base em cada lado, os expoentes devem ser iguais. Isso também se aplica quando os expoentes são expressões algébricas. Portanto, podemos resolver muitas equações exponenciais usando as regras dos expoentes para reescrever cada lado como uma potência com a mesma base. Em seguida, usamos o fato de que as funções exponenciais são individuais para definir os expoentes iguais entre si e resolver o desconhecido.
Por exemplo, considere a equação\(3^{4x−7}=\dfrac{3^{2x}}{3}\). Para resolver\(x\), usamos a propriedade de divisão dos expoentes para reescrever o lado direito para que ambos os lados tenham a base comum,\(3\). Em seguida, aplicamos a propriedade um-para-um dos expoentes definindo os expoentes iguais um ao outro e resolvendo para\(x\):
\[\begin{align*} 3^{4x-7}&= \dfrac{3^{2x}}{3}\\ 3^{4x-7}&= \dfrac{3^{2x}}{3^1} \qquad &&\text{Rewrite 3 as } 3^1\\ 3^{4x-7}&= 3^{2x-1} \qquad &&\text{Use the division property of exponents}\\ 4x-7&= 2x-1 \qquad &&\text{Apply the one-to-one property of exponents}\\ 2x&= 6 \qquad &&\text{Subtract 2x and add 7 to both sides}\\ x&= 3 \qquad &&\text{Divide by 3} \end{align*}\]
Para qualquer expressão algébrica\(S\) e\(T\) qualquer número real positivo\(b≠1\),
\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]
- Use as regras dos expoentes para simplificar, se necessário, para que a equação resultante tenha a forma\(b^S=b^T\).
- Use a propriedade um-para-um para definir os expoentes iguais.
- Resolva a equação resultante,\(S=T\), para o desconhecido.
Resolver\(2^{x−1}=2^{2x−4}\).
Solução
\[\begin{align*} 2^{x-1}&= 2^{2x-4} \qquad &&\text{The common base is 2}\\ x-1&= 2x-4 \qquad &&\text{By the one-to-one property the exponents must be equal}\\ x&= 3 \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(5^{2x}=5^{3x+2}\).
- Responda
-
\(x=−2\)
Reescreva equações para que todas as potências tenham a mesma base
Às vezes, a base comum para uma equação exponencial não é mostrada explicitamente. Nesses casos, simplesmente reescrevemos os termos na equação como potências com uma base comum e resolvemos usando a propriedade um-para-um.
Por exemplo, considere a equação\(256=4^{x−5}\). Podemos reescrever os dois lados dessa equação como uma potência de\(2\). Em seguida, aplicamos as regras dos expoentes, junto com a propriedade um-para-um, para resolver\(x\):
\[\begin{align*} 256&= 4^{x-5}\\ 2^8&= {(2^2)}^{x-5} \qquad &&\text{Rewrite each side as a power with base 2}\\ 2^8&= 2^{2x-10} \qquad &&\text{Use the one-to-one property of exponents}\\ 8&= 2x-10 \qquad &&\text{Apply the one-to-one property of exponents}\\ 18&= 2x \qquad &&\text{Add 10 to both sides}\\ x&= 9 \qquad &&\text{Divide by 2} \end{align*}\]
- Reescreva cada lado da equação como uma potência com uma base comum.
- Use as regras dos expoentes para simplificar, se necessário, para que a equação resultante tenha a forma\(b^S=b^T\).
- Use a propriedade um-para-um para definir os expoentes iguais.
- Resolva a equação resultante,\(S=T\), para o desconhecido.
Resolver\(8^{x+2}={16}^{x+1}\).
Solução
\[\begin{align*} 8^{x+2}&= {16}^{x+1}\\ {(2^3)}^{x+2}&= {(2^4)}^{x+1} \qquad &&\text{Write 8 and 16 as powers of 2}\\ 2^{3x+6}&= 2^{4x+4} \qquad &&\text{To take a power of a power, multiply exponents}\\ 3x+6&= 4x+4 \qquad &&\text{Use the one-to-one property to set the exponents equal}\\ x&= 2 \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(5^{2x}={25}^{3x+2}\).
- Responda
-
\(x=−1\)
Resolver\(2^{5x}=\sqrt{2}\).
Solução
\[\begin{align*} 2^{5x}&= 2^{\frac{1}{2}} \qquad &&\text{Write the square root of 2 as a power of 2}\\ 5x&= \dfrac{1}{2} \qquad &&\text{Use the one-to-one property}\\ x&= \dfrac{1}{10} \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(5^x=\sqrt{5}\).
- Responda
-
\(x=\dfrac{1}{2}\)
Não. Lembre-se de que o alcance de uma função exponencial é sempre positivo. Ao resolver a equação, podemos obter uma expressão indefinida.
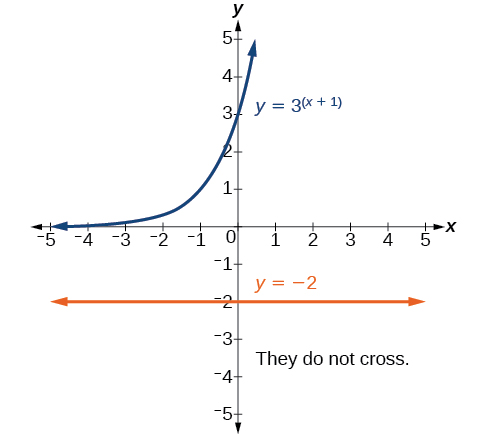
Resolver\(3^{x+1}=−2\).
Solução
Essa equação não tem solução. Não existe um valor real\(x\) que torne a equação uma afirmação verdadeira porque qualquer potência de um número positivo é positiva.
Análise
A figura\(\PageIndex{2}\) mostra que os dois gráficos não se cruzam, então o lado esquerdo nunca é igual ao lado direito. Portanto, a equação não tem solução.
Resolver\(2^x=−100\).
- Responda
-
A equação não tem solução.
Resolvendo equações exponenciais usando logaritmos
Às vezes, os termos de uma equação exponencial não podem ser reescritos com uma base comum. Nesses casos, resolvemos usando o logaritmo de cada lado. Lembre-se, como\(\log(a)=\log(b)\) é equivalente a\(a=b\), podemos aplicar logaritmos com a mesma base em ambos os lados de uma equação exponencial.
- Aplique o logaritmo dos dois lados da equação.
- Se um dos termos na equação tiver base 10, use o logaritmo comum.
- Se nenhum dos termos na equação tiver base 10, use o logaritmo natural.
- Use as regras dos logaritmos para resolver o desconhecido.
Resolver\(5^{x+2}=4^x\).
Solução
\ [\ begin {align*}
5^ {x+2} &= 4^x\ qquad &&\ text {Não há uma maneira fácil de fazer com que os poderes tenham a mesma base}\\\ ln5^ {x+2} &=
\ ln4^x\ qquad &&\ text {Pegue ln de ambos os lados}\\
(x+2)\ ln5&= x\ ln5&= x\ ln5&= x\ ln5&= x\ ln4 n4\ quad &&\ text {Use as leis dos registros}\\
x\ ln5+2\ ln5&= x\ ln4\ qquad &&\ text {Use a lei distributiva}\\
x\ ln5-x\ ln4&= -2\ ln5\ qquad &&\ text {Obtenha termos contendo x de um lado, termos sem x no outro}\\
x (\ ln5-\ ln4) &=\ ln4 n5\ qquad &&\ text {No lado esquerdo, anote um x} \\
x\ ln\ left (\ dfrac {5} {4}\ right) &=\ ln\ left (\ dfrac {1} {25}\ right)\ quad &&\ text {Use as leis dos logs}\\
x&=\ dfrac {\ ln\ left (\ dfrac {1} {25}\ right)} {\ ln\ left (\ dfrac {1} {25}\ right)} {\ ln\ left (\ dfrac {1} {25}\ right)} {\ ln\ left (\ dfrac {1} {25}\ right)} {\ ln {5} {4}\ right)}\ qquad &&\ text {Divida pelo coeficiente de x}
\ end { alinhamento*}\]
Resolver\(2^x=3^{x+1}\).
- Responda
-
\(x=\dfrac{\ln3}{\ln \left (\dfrac{2}{3} \right )}\)
Sim. A solução é\(0\).
Equações contendo\(e\)
Um tipo comum de equações exponenciais são aquelas com base\(e\). Essa constante ocorre repetidamente na natureza, na matemática, na ciência, na engenharia e nas finanças. Quando temos uma equação com uma\(e\) base em cada lado, podemos usar o logaritmo natural para resolvê-la.
- Divida os dois lados da equação por\(A\).
- Aplique o logaritmo natural dos dois lados da equação.
- Divida os dois lados da equação por\(k\).
Resolver\(100=20e^{2t}\).
Solução
\[\begin{align*} 100&= 20e^{2t}\\ 5&= e^{2t} \qquad &&\text{Divide by the coefficient of the power}\\ \ln5&= 2t \qquad &&\text{Take ln of both sides. Use the fact that } ln(x) \text{ and } e^x \text{ are inverse functions}\\ t&= \dfrac{\ln5}{2} \qquad &&\text{Divide by the coefficient of t} \end{align*}\]
Análise
Usando leis de registros, também podemos escrever essa resposta no formulário\(t=\ln\sqrt{5}\). Se quisermos uma aproximação decimal da resposta, usamos uma calculadora.
Resolver\(3e^{0.5t}=11\).
- Responda
-
\(t=2\ln \left (\dfrac{11}{3} \right )\)ou\(\ln{ \left (\dfrac{11}{3} \right )}^2\)
Não. Há uma solução quando\(k≠0\), quando\(y\) e\(A\) são ambos 0 ou nenhum 0, e eles têm o mesmo sinal. Um exemplo de uma equação com essa forma que não tem solução é\(2=−3e^t\).
Resolver\(4e^{2x}+5=12\).
Solução
\[\begin{align*} 4e^{2x}+5&= 12\\ 4e^{2x}&= 7 \qquad &&\text{Combine like terms}\\ e^{2x}&= \dfrac{7}{4} \qquad &&\text{Divide by the coefficient of the power}\\ 2x&= \ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Take ln of both sides}\\ x&= \dfrac{1}{2}\ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(3+e^{2t}=7e^{2t}\).
- Responda
-
\(t=\ln \left (\dfrac{1}{\sqrt{2}} \right )=−\dfrac{1}{2}\ln(2)\)
Soluções estranhas
Às vezes, os métodos usados para resolver uma equação introduzem uma solução estranha, que é uma solução que está correta algebricamente, mas não satisfaz as condições da equação original. Uma dessas situações surge na resolução quando o logaritmo é obtido em ambos os lados da equação. Nesses casos, lembre-se de que o argumento do logaritmo deve ser positivo. Se o número que estamos avaliando em uma função logarítmica for negativo, não haverá saída.
Resolver\(e^{2x}−e^x=56\).
Solução
\[\begin{align*} e^{2x}-e^x&= 56\\ e^{2x}-e^x-56&= 0 \qquad &&\text{Get one side of the equation equal to zero}\\ (e^x+7)(e^x-8)&= 0 \qquad &&\text{Factor by the FOIL method}\\ e^x+7&= 0 \qquad &&\text{or} \\ e^x-8&= 0 \qquad &&\text{If a product is zero, then one factor must be zero}\\ e^x&= -7 \qquad &&\text{or} \\ e^x&= 8 \qquad &&\text{Isolate the exponentials}\\ e^x&= 8 \qquad &&\text{Reject the equation in which the power equals a negative number}\\ x&= \ln8 \qquad &&\text{Solve the equation in which the power equals a positive number} \end{align*}\]
Análise
Quando planejamos usar a fatoração para resolver um problema, sempre obtemos zero em um lado da equação, porque zero tem a propriedade única de que quando um produto é zero, um ou ambos os fatores devem ser zero. Rejeitamos a equação\(e^x=−7\) porque um número positivo nunca é igual a um número negativo. A solução não\(\ln(−7)\) é um número real e, no sistema de números reais, essa solução é rejeitada como uma solução estranha.
Resolver\(e^{2x}=e^x+2\).
- Responda
-
\(x=\ln2\)
Não. Lembre-se de que só podemos aplicar o logaritmo a um número positivo. Sempre verifique se há soluções estranhas.
Usando a definição de um logaritmo para resolver equações logarítmicas
Já vimos que toda equação logarítmica\({\log}_b(x)=y\) é equivalente à equação exponencial\(b^y=x\). Podemos usar esse fato, junto com as regras dos logaritmos, para resolver equações logarítmicas em que o argumento é uma expressão algébrica.
Por exemplo, considere a equação\({\log}_2(2)+{\log}_2(3x−5)=3\). Para resolver essa equação, podemos usar regras de logaritmos para reescrever o lado esquerdo em formato compacto e, em seguida, aplicar a definição de registros para resolver\(x\):
\[\begin{align*} {\log}_2(2)+{\log}_2(3x-5)&= 3\\ {\log}_2(2(3x-5))&= 3 \qquad \text{Apply the product rule of logarithms}\\ {\log}_2(6x-10)&= 3 \qquad \text{Distribute}\\ 2^3&= 6x-10 \qquad \text{Apply the definition of a logarithm}\\ 8&= 6x-10 \qquad \text{Calculate } 2^3\\ 18&= 6x \qquad \text{Add 10 to both sides}\\ x&= 3 \qquad \text{Divide by 6} \end{align*}\]
Para qualquer expressão algébrica\(S\) e números reais\(b\) e\(c\), onde\(b>0\)\(b≠1\),
\[\begin{align} {\log}_b(S)=c \text{ if and only if } b^c=S \end{align}\]
Resolver\(2\ln x+3=7\).
Solução
\[\begin{align*} 2\ln x+3&= 7\\ 2\ln x&= 4 \qquad \text{Subtract 3}\\ \ln x&= 2 \qquad \text{Divide by 2}\\ x&= e^2 \qquad \text{Rewrite in exponential form} \end{align*}\]
Resolver\(6+\ln x=10\).
- Responda
-
\(x=e^4\)
Resolver\(2\ln(6x)=7\).
Solução
\[\begin{align*} 2\ln(6x)&= 7\\ \ln(6x)&= \dfrac{7}{2} \qquad \text{Divide by 2}\\ 6x&= e^{\left (\dfrac{7}{2} \right )} \qquad \text{Use the definition of }\ln \\ x&= \dfrac{1}{6}e^{\left (\dfrac{7}{2} \right )} \qquad \text{Divide by 6} \end{align*}\]
Resolver\(2\ln(x+1)=10\).
- Responda
-
\(x=e^5−1\)
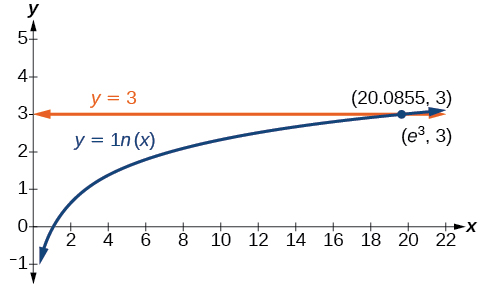
Resolver\(\ln x=3\).
Solução
\[\begin{align*} \ln x&= 3\\ x&= e^3 \qquad \text{Use the definition of the natural logarithm} \end{align*}\]
\(\PageIndex{3}\)A figura representa o gráfico da equação. No gráfico, a coordenada x do ponto em que os dois gráficos se cruzam está próxima\(20\). Em outras palavras\(e^3≈20\). Uma calculadora fornece uma melhor aproximação:\(e^3≈20.0855\).
Use uma calculadora gráfica para estimar a solução aproximada da equação logarítmica em\(2\) casas\(2^x=1000\) decimais.
- Responda
-
\(x≈9.97\)
Usando a propriedade um-para-um dos logaritmos para resolver equações logarítmicas
Assim como acontece com as equações exponenciais, podemos usar a propriedade um-para-um para resolver equações logarítmicas. A propriedade um-para-um das funções logarítmicas nos diz que, para qualquer número\(x>0\) real\(T>0\) e qualquer número real positivo\(b\), onde\(b≠1\),\(S>0\)
\({\log}_bS={\log}_bT\)se e somente se\(S=T\).
Por exemplo,
Se\({\log}_2(x−1)={\log}_2(8)\), então\(x−1=8\).
Então, se\(x−1=8\), então podemos resolver para\(x\), e obtemos\(x=9\). Para verificar, podemos substituir\(x=9\) na equação original:\({\log}_2(9−1)={\log}_2(8)=3\). Em outras palavras, quando uma equação logarítmica tem a mesma base em cada lado, os argumentos devem ser iguais. Isso também se aplica quando os argumentos são expressões algébricas. Portanto, quando é dada uma equação com registros da mesma base em cada lado, podemos usar regras de logaritmos para reescrever cada lado como um único logaritmo. Em seguida, usamos o fato de que as funções logarítmicas são individuais para definir os argumentos iguais entre si e resolver o desconhecido.
Por exemplo, considere a equação\(\log(3x−2)−\log(2)=\log(x+4)\). Para resolver essa equação, podemos usar as regras dos logaritmos para reescrever o lado esquerdo como um único logaritmo e, em seguida, aplicar a propriedade um-para-um para resolver\(x\):
\[\begin{align*} \log(3x-2)-\log(2)&= \log(x+4)\\ \log \left (\dfrac{3x-2}{2} \right )&= \log(x+4) \qquad \text{Apply the quotient rule of logarithms}\\ \dfrac{3x-2}{2}&= x+4 \qquad \text{Apply the one to one property of a logarithm}\\ 3x-2&= 2x+8 \qquad \text{Multiply both sides of the equation by 2}\\ x&= 10 \qquad \text{Subtract 2x and add 2} \end{align*}\]
Para verificar o resultado,\(x=10\) substitua por\(\log(3x−2)−\log(2)=\log(x+4)\).
\[\begin{align*} \log(3(10)-2)-\log(2)&= \log((10)+4) \\ \log(28)-\log(2)&= \log(14)\\ \log \left (\dfrac{28}{2} \right )&= \log(14) \qquad \text{The solution checks} \end{align*}\]
Para qualquer expressão algébrica\(S\)\(T\) e qualquer número real positivo\(b\), onde\(b≠1\),
\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]
Observe que, ao resolver uma equação envolvendo logaritmos, sempre verifique se a resposta está correta ou se é uma solução estranha.
- Use as regras dos logaritmos para combinar termos semelhantes, se necessário, para que a equação resultante tenha a forma\({\log}_bS={\log}_bT\).
- Use a propriedade um-para-um para definir os argumentos iguais.
- Resolva a equação resultante,\(S=T\), para o desconhecido.
Resolver\(\ln(x^2)=\ln(2x+3)\).
Solução
\[\begin{align*} \ln(x^2)&= \ln(2x+3)\\ x^2&= 2x+3 \qquad \text{Use the one-to-one property of the logarithm}\\ x^2-2x-3&= 0 \qquad \text{Get zero on one side before factoring}\\ (x-3)(x+1)&= 0 \qquad \text{Factor using FOIL}\\ x-3&= 0 \qquad \text{or } x+1=0 \text{ If a product is zero, one of the factors must be zero}\\ x=3 \qquad \text{or} \\ x&= -11 \qquad \text{Solve for x} \end{align*}\]
Análise
Existem duas soluções:\(3\) ou\(−1\). A solução\(−1\) é negativa, mas é verificada quando substituída na equação original porque o argumento das funções logarítmicas ainda é positivo.
Resolver\(\ln(x^2)=\ln1\).
- Responda
-
\(x=1\)ou\(x=−1\)
Resolvendo problemas aplicados usando equações exponenciais e logarítmicas
Nas seções anteriores, aprendemos as propriedades e regras para funções exponenciais e logarítmicas. Vimos que qualquer função exponencial pode ser escrita como uma função logarítmica e vice-versa. Usamos expoentes para resolver equações logarítmicas e logaritmos para resolver equações exponenciais. Agora estamos prontos para combinar nossas habilidades para resolver equações que modelam situações do mundo real, seja o desconhecido em um expoente ou no argumento de um logaritmo.
Uma dessas aplicações é na ciência, no cálculo do tempo necessário para que metade do material instável em uma amostra de uma substância radioativa se decomponha, chamada de meia-vida. A tabela\(\PageIndex{1}\) lista a meia-vida de várias das substâncias radioativas mais comuns.
| Substância | Use | Meia-vida |
|---|---|---|
| gálio-67 | medicina nuclear | 80 horas |
| cobalto-60 | fabricação | 5,3 anos |
| tecnécio-99m | medicina nuclear | 6 horas |
| amerício-241 | construção | 432 anos |
| carbono-14 | datação arqueológica | 5.715 anos |
| urânio-235 | potência atômica | 703.800.000 anos |
Podemos ver o quanto as meias-vidas dessas substâncias variam. Saber a meia-vida de uma substância nos permite calcular a quantidade restante após um tempo especificado. Podemos usar a fórmula para decaimento radioativo:
\[\begin{align} A(t)&= A_0e^{\tfrac{\ln(0.5)}{T}t}\\ A(t)&= A_0e^{\tfrac{\ln(0.5)t}{T}}\\ A(t)&= A_0{(e^{\ln(0.5)})}^{\tfrac{t}{T}}\\ A(t)&= A_0{\left (\dfrac{1}{2}\right )}^{\tfrac{t}{T}}\\ \end{align}\]
onde
- \(A_0\)é a quantidade inicialmente presente
- \(T\)é a meia-vida da substância
- \(t\)é o período de tempo durante o qual a substância é estudada
- \(y\)é a quantidade da substância presente após o tempo\(t\)
Quanto tempo levará para que dez por cento de uma amostra de\(1000\) -grama de urânio-235 se decomponha?
Solução
\[\begin{align*} y&= 1000e^{\tfrac{\ln(0.5)}{703,800,000}t}\\ 900&= 1000e^{\tfrac{\ln(0.5)}{703,800,000}t} \qquad \text{After } 10\% \text{ decays, 900 grams are left}\\ 0.9&= e^{\tfrac{\ln(0.5)}{703,800,000}t} \qquad \text{Divide by 1000}\\ \ln(0.9)&= \ln \left (e^{\tfrac{\ln(0.5)}{703,800,000}t} \right ) \qquad \text{Take ln of both sides}\\ \ln(0.9)&= \dfrac{\ln(0.5)}{703,800,000}t \qquad \ln(e^M)=M\\ t&= 703,800,000\times \dfrac{\ln(0.9)}{\ln(0.5)} \qquad \text{years Solve for t}\\ t&\approx 106,979,777 \qquad \text{years} \end {align*} \]
Análise
Dez por cento dos\(1000\) gramas são\(100\) gramas. Se\(100\) os gramas se decompõem, a quantidade restante de urânio-235 é de\(900\) gramas.
Quanto tempo demorará até que vinte por cento da nossa amostra de 1000 gramas de urânio-235 tenha decaído?
- Responda
-
\(t=703,800,000×\dfrac{\ln(0.8)}{\ln(0.5)}\)anos ≈ 226.572.993 anos.
Acesse esses recursos on-line para obter instruções e práticas adicionais com equações exponenciais e logarítmicas.
- Resolvendo equações logarítmicas
- Resolvendo equações exponenciais com logaritmos
Equações-chave
| Propriedade individual para funções exponenciais | Para qualquer expressão algébrica\(S\)\(T\) e qualquer número real positivo\(b\), onde\(b^S=b^T\) se e somente se\(S=T\). |
| Definição de um logaritmo | Para qualquer expressão algébrica S e números reais positivos\(b\) e\(c\), onde\(b≠1\),\({\log}_b(S)=c\) se e somente se\(b^c=S\). |
| Propriedade individual para funções logarítmicas | Para qualquer expressão algébrica\(S\)\(T\) e qualquer número real positivo\(b\), onde\(b≠1\), \({\log}_bS={\log}_bT\) se e somente se\(S=T\). |
Conceitos-chave
- Podemos resolver muitas equações exponenciais usando as regras dos expoentes para reescrever cada lado como uma potência com a mesma base. Em seguida, usamos o fato de que as funções exponenciais são individuais para definir os expoentes iguais entre si e resolver o desconhecido.
- Quando recebemos uma equação exponencial em que as bases são explicitamente mostradas como iguais, defina os expoentes iguais um ao outro e resolva o desconhecido. Veja o exemplo\(\PageIndex{1}\).
- Quando recebemos uma equação exponencial em que as bases não são explicitamente mostradas como iguais, reescreva cada lado da equação como potências da mesma base, depois defina os expoentes iguais um ao outro e resolva o desconhecido. Veja exemplo\(\PageIndex{2}\)\(\PageIndex{3}\), exemplo e exemplo\(\PageIndex{4}\).
- Quando uma equação exponencial não pode ser reescrita com uma base comum, resolva usando o logaritmo de cada lado. Veja o exemplo\(\PageIndex{5}\).
- Podemos resolver equações exponenciais com base\(e\), aplicando o logaritmo natural de ambos os lados porque as funções exponenciais e logarítmicas são inversas uma da outra. Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
- Depois de resolver uma equação exponencial, verifique cada solução na equação original para encontrar e eliminar quaisquer soluções estranhas. Veja o exemplo\(\PageIndex{8}\).
- Quando é dada uma equação da forma\({\log}_b(S)=c\), onde\(S\) está uma expressão algébrica, podemos usar a definição de um logaritmo para reescrever a equação como a equação\(b^c=S\) exponencial equivalente e resolver o desconhecido. Veja o exemplo\(\PageIndex{9}\) e o exemplo\(\PageIndex{10}\).
- Também podemos usar gráficos para resolver equações com o formulário\({\log}_b(S)=c\). Representamos graficamente as duas equações\(y={\log}_b(S)\) e\(y=c\) no mesmo plano de coordenadas e identificamos a solução como o valor x do ponto de interseção. Veja o exemplo\(\PageIndex{11}\).
- Quando é dada uma equação da forma\({\log}_bS={\log}_bT\), onde\(S\) e\(T\) são expressões algébricas, podemos usar a propriedade um-para-um dos logaritmos para resolver a equação\(S=T\) para o desconhecido. Veja o exemplo\(\PageIndex{12}\).
- Combinando as habilidades aprendidas nesta e nas seções anteriores, podemos resolver equações que modelam situações do mundo real, seja o desconhecido em um expoente ou no argumento de um logaritmo. Veja o exemplo\(\PageIndex{13}\).


