2.4: Ajustando modelos lineares aos dados

Objetivos de

• Desenhe e interprete diagramas de dispersão.
• Use um utilitário gráfico para encontrar a linha mais adequada.
• Faça a distinção entre relações lineares e não lineares.
• Ajuste uma linha de regressão a um conjunto de dados e use o modelo linear para fazer previsões.

Um professor está tentando identificar tendências entre as notas do exame final. Sua turma tem uma mistura de alunos, então ele se pergunta se existe alguma relação entre a idade e as notas do exame final. Uma forma de ele analisar as notas é criar um diagrama que relaciona a idade de cada aluno com a nota do exame recebida. Nesta seção, examinaremos um desses diagramas conhecido como gráfico de dispersão.

Desenho e interpretação de gráficos de dispersão

Um gráfico de dispersão é um gráfico de pontos representados graficamente que pode mostrar uma relação entre dois conjuntos de dados. Se a relação for de um modelo linear, ou de um modelo quase linear, o professor pode tirar conclusões usando seu conhecimento de funções lineares. A figura\(\PageIndex{1}\) mostra um gráfico de dispersão de amostra.

Figura\(\PageIndex{1}\): Um gráfico de dispersão das variáveis de idade e pontuação do exame final

Observe que esse gráfico de dispersão não indica uma relação linear. Os pontos não parecem seguir uma tendência. Em outras palavras, não parece haver uma relação entre a idade do aluno e a pontuação no exame final.

Exemplo\(\PageIndex{1}\): Using a Scatter Plot to Investigate Cricket Chirps

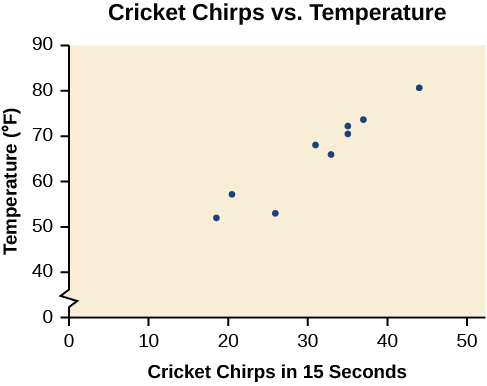
A tabela mostra o número de chilros de críquete em 15 segundos, para várias temperaturas do ar diferentes, em graus Fahrenheit [1]. Faça um gráfico desses dados e determine se os dados parecem estar relacionados linearmente.

Tabela\(\PageIndex{1}\)

chilreios	44	35	20,4	33	31	35	18,5	37	26
Temperatura	80,5	70,5	57	66	68	72	52	73,5	53

Solução

A plotagem desses dados, conforme ilustrado na Figura,\(\PageIndex{2}\) sugere que pode haver uma tendência. Podemos ver pela tendência dos dados que o número de chilros aumenta à medida que a temperatura aumenta. A tendência parece ser aproximadamente linear, embora certamente não seja perfeita.

Figura\(\PageIndex{2}\): A regressão de linha geralmente é positiva.

Encontrando a linha mais adequada

Quando reconhecemos a necessidade de uma função linear para modelar esses dados, a pergunta natural de acompanhamento é “o que é essa função linear?” Uma forma de aproximar nossa função linear é esboçar a linha que parece melhor se ajustar aos dados. Então, podemos estender a linha até podermos verificar o intercepto y. Podemos aproximar a inclinação da linha estendendo-a até podermos estimar\(\frac{\text{rise}}{\text{run}}\) o.

Exemplo\(\PageIndex{2}\): Finding a Line of Best Fit

Encontre uma função linear que se ajuste aos dados na Tabela\(\PageIndex{1}\) “observando” uma linha que parece se encaixar.

Solução

Em um gráfico, poderíamos tentar esboçar uma linha.

Usando os pontos inicial e final de nossa linha desenhada à mão, pontos\((0, 30)\) e\((50, 90)\), este gráfico tem uma inclinação de

\[m=\dfrac{60}{50}=1.2\]

e um intercepto y em 30. Isso dá uma equação de

\[T(c)=1.2c+30\]

onde\(c\) está o número de chilros em 15 segundos e\(T(c)\) é a temperatura em graus Fahrenheit. A equação resultante é representada na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Gráfico de dispersão, mostrando a linha de melhor ajuste.

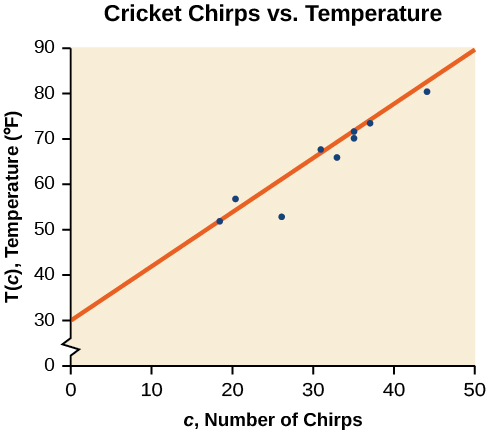
Análise

Essa equação linear pode então ser usada para aproximar as respostas a várias perguntas que podemos fazer sobre a tendência.

Reconhecendo interpolação ou extrapolação

Embora os dados da maioria dos exemplos não caiam perfeitamente na linha, a equação é nossa melhor suposição sobre como a relação se comportará fora dos valores para os quais temos dados. Usamos um processo conhecido como interpolação quando prevemos um valor dentro do domínio e do intervalo dos dados. O processo de extrapolação é usado quando prevemos um valor fora do domínio e do intervalo dos dados.

A figura\(\PageIndex{4}\) compara os dois processos para os dados de cricket-chirp abordados no Example\(\PageIndex{2}\). Podemos ver que a interpolação ocorreria se usássemos nosso modelo para prever a temperatura quando os valores de chirps estivessem entre 18,5 e 44. A extrapolação ocorreria se usássemos nosso modelo para prever a temperatura quando os valores de chiados fossem menores que 18,5 ou maiores que 44.

Há uma diferença entre fazer previsões dentro do domínio e da faixa de valores para os quais temos dados e fora desse domínio e intervalo. Prever um valor fora do domínio e do intervalo tem suas limitações. Quando nosso modelo não se aplica mais após um certo ponto, às vezes é chamado de avaria do modelo. Por exemplo, prever uma função de custo por um período de dois anos pode envolver o exame dos dados em que a entrada é o tempo em anos e a saída é o custo. Mas se tentarmos extrapolar um custo quando\(x=50\), ou seja, em 50 anos, o modelo não se aplicaria porque não poderíamos contabilizar os fatores cinquenta anos no futuro.

Figura\(\PageIndex{4}\): A interpolação ocorre dentro do domínio e do intervalo dos dados fornecidos, enquanto a extrapolação ocorre fora.

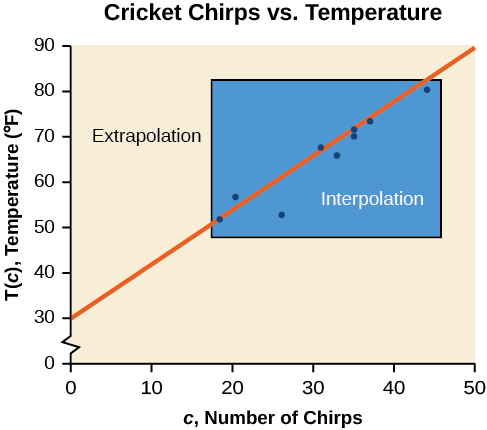
Interpolação e extrapolação

Diferentes métodos de fazer previsões são usados para analisar dados.

• O método de extrapolação envolve a previsão de um valor fora do domínio e/ou do intervalo dos dados.
• A falha do modelo ocorre no momento em que o modelo não se aplica mais.

Exemplo\(\PageIndex{3}\): Understanding Interpolation and Extrapolation

Use os dados de críquete da Tabela\(\PageIndex{1}\) para responder às seguintes perguntas:

1. Prever a temperatura quando os grilos cantam 30 vezes em 15 segundos seria interpolação ou extrapolação? Faça a previsão e discuta se é razoável.
2. Prever o número de chilros que os grilos produzirão a 40 graus seria interpolação ou extrapolação? Faça a previsão e discuta se é razoável.

Solução

a. O número de chilros nos dados fornecidos variou de 18,5 a 44. Uma previsão de 30 chirps por 15 segundos está dentro do domínio de nossos dados, assim como a interpolação. Usando nosso modelo:

\[\begin{align} T(30)&=30+1.2(30) \\ &=66 \text{ degrees} \end{align}\]

Com base nos dados que temos, esse valor parece razoável.
b. Os valores de temperatura variaram de 52 a 80,5. Prever o número de chilros a 40 graus é extrapolação porque 40 está fora da faixa de nossos dados. Usando nosso modelo:

\[\begin{align} 40&=30+1.2c \\ 10&=1.2c \\ c&\approx8.33 \end{align}\]

Podemos comparar as regiões de interpolação e extrapolação usando a Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Gráfico de dispersão, mostrando a linha de melhor ajuste e onde a interpolação e extrapolação ocorrem.

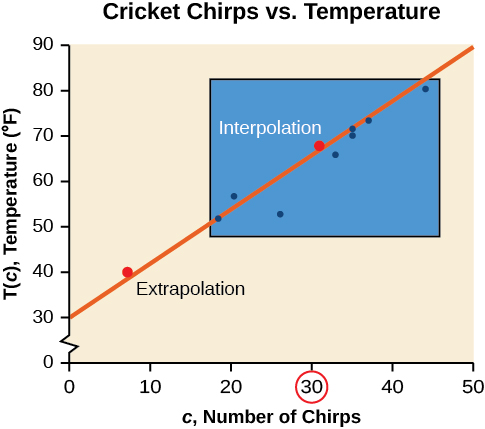
Análise

Nosso modelo prevê que os grilos cantariam 8,33 vezes em 15 segundos. Embora isso possa ser possível, não temos motivos para acreditar que nosso modelo seja válido fora do domínio e da faixa. Na verdade, geralmente os grilos param de cantar completamente abaixo de cerca de 50 graus.

Exercício\(\PageIndex{1}\)

De acordo com os dados da Tabela\(\PageIndex{1}\), qual temperatura podemos prever se contarmos 20 chilros em 15 segundos?

Solução

54°F

Encontrando a linha de melhor ajuste usando um utilitário gráfico

Embora observar uma linha funcione razoavelmente bem, existem técnicas estatísticas para ajustar uma linha aos dados que minimizam as diferenças entre a linha e os valores dos dados [2]. Uma dessas técnicas é chamada de regressão de mínimos quadrados e pode ser computada por muitas calculadoras gráficas, software de planilhas, software estatístico e muitas calculadoras baseadas na web [3]. A regressão de mínimos quadrados é um meio de determinar a linha que melhor se ajusta aos dados, e aqui nos referiremos a esse método como regressão linear.

Dados de entrada e saídas correspondentes de uma função linear, encontre a melhor linha de ajuste usando regressão linear.

1. Insira a entrada na Lista 1 (L1).
2. Insira a saída na Lista 2 (L2).
3. Em um utilitário gráfico, selecione Regressão linear (LinReg).

Exemplo\(\PageIndex{4}\): Finding a Least Squares Regression Line

Encontre a linha de regressão de mínimos quadrados usando os dados de grilo na tabela\(\PageIndex{1}\).

Solução

Insira a entrada (chirps) na Lista 1 (L1).
Insira a saída (temperatura) na Lista 2 (L2). Veja a tabela\(\PageIndex{2}\).

Tabela\(\PageIndex{2}\)

L1	44	35	20,4	33	31	35	18,5	37	26
L2	80,5	70,5	57	66	68	72	52	73,5	53

Em um utilitário gráfico, selecione Regressão linear (LinReg). Usando os dados anteriores do chilro de críquete, com a tecnologia, obtemos a equação:

\[T(c)=30.281+1.143c\]

Análise

Observe que essa linha é bastante semelhante à equação que “observamos”, mas deve se ajustar melhor aos dados. Observe também que o uso dessa equação mudaria nossa previsão de temperatura ao ouvir 30 chiados em 15 segundos de 66 graus para:

\[\begin{align} T(30)&=30.281+1.143(30) \\ &=64.571 \\ &\approx 64.6 \text{ degrees} \end{align}\]

O gráfico do gráfico de dispersão com a linha de regressão de mínimos quadrados é mostrado na Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Gráfico de dispersão, mostrando a linha de melhor ajuste.

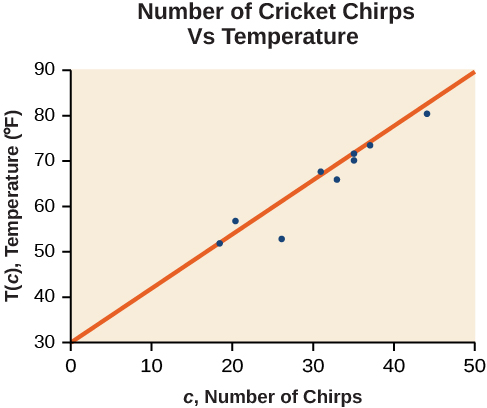
Alguma vez haverá um caso em que duas linhas diferentes servirão como a melhor opção para os dados?

Não. Existe apenas uma linha de melhor ajuste.

Distinguindo entre modelos lineares e não lineares

Como vimos acima com o modelo cricket-chirp, alguns dados apresentam fortes tendências lineares, mas outros dados, como as notas do exame final plotadas por idade, são claramente não lineares. A maioria das calculadoras e softwares de computador também podem nos fornecer o coeficiente de correlação, que é uma medida de quão perto a linha se ajusta aos dados. Muitas calculadoras gráficas exigem que o usuário ative uma seleção de “diagnóstico” para encontrar o coeficiente de correlação, que os matemáticos rotulam como\(r\). O coeficiente de correlação fornece uma maneira fácil de ter uma ideia de quão perto de uma linha os dados estão.

Devemos calcular o coeficiente de correlação somente para dados que seguem um padrão linear ou para determinar o grau em que um conjunto de dados é linear. Se os dados exibirem um padrão não linear, o coeficiente de correlação para uma regressão linear não tem sentido. Para ter uma ideia da relação entre o valor de\(r\) e o gráfico dos dados, a Figura\(\PageIndex{7}\) mostra alguns grandes conjuntos de dados com seus coeficientes de correlação. Lembre-se de que, para todos os gráficos, o eixo horizontal mostra a entrada e o eixo vertical mostra a saída.

Figura\(\PageIndex{7}\): Dados plotados e coeficientes de correlação relacionados. (crédito: “Denis Boigelot”, Wikimedia Commons)

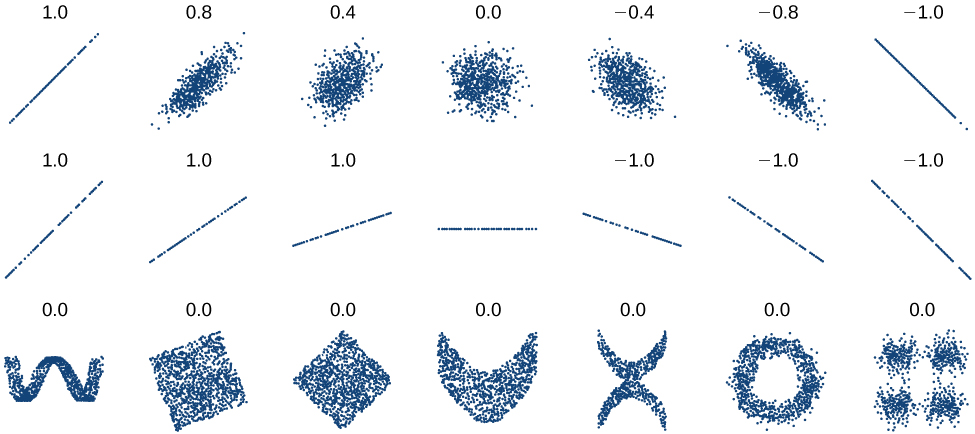
Coeficiente de correlação

O coeficiente de correlação é um valor\(r\),, entre —1 e 1.

• \(r>0\)sugere uma relação positiva (crescente)
• \(r<0\)sugere uma relação negativa (decrescente)
• Quanto mais próximo o valor estiver de 0, mais dispersos serão os dados.
• Quanto mais próximo o valor estiver de 1 ou —1, menos dispersos serão os dados.

Exemplo\(\PageIndex{5}\): Finding a Correlation Coefficient

Calcule o coeficiente de correlação para dados de grilo na tabela\(\PageIndex{1}\).

Solução

Como os dados parecem seguir um padrão linear, podemos usar a tecnologia para calcular\(r\). Insira as entradas e saídas correspondentes e selecione a Regressão linear. A calculadora também fornecerá o coeficiente de correlação,\(r=0.9509\). Esse valor é muito próximo de 1, o que sugere uma forte relação linear crescente.

Nota: Para algumas calculadoras, o Diagnóstico deve estar “ativado” para obter o coeficiente de correlação quando a regressão linear é realizada: [2nd] > [0] > [alpha] [x—1] e, em seguida, vá até DIAGNOSTICSON.

Prevendo com uma linha de regressão

Depois de determinarmos que um conjunto de dados é linear usando o coeficiente de correlação, podemos usar a linha de regressão para fazer previsões. Como aprendemos acima, uma linha de regressão é a linha que está mais próxima dos dados no gráfico de dispersão, o que significa que apenas uma dessas linhas é a melhor opção para os dados.

Exemplo\(\PageIndex{6}\): Using a Regression Line to Make Predictions

O consumo de gasolina nos Estados Unidos tem aumentado constantemente. Os dados de consumo de 1994 a 2004 são mostrados na Tabela\(\PageIndex{3}\). Determine se a tendência é linear e, em caso afirmativo, encontre um modelo para os dados. Use o modelo para prever o consumo em 2008.

Tabela\(\PageIndex{3}\)

Ano	94	95	96	97	98	1999	'00	'01	'02	2003	2004
Consumo (bilhões de galões)	113	116	118	119	123	125	126	128	131	133	136

O gráfico de dispersão dos dados, incluindo a linha de regressão de mínimos quadrados, é mostrado na Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\): Gráfico de dispersão, mostrando a linha de melhor ajuste.

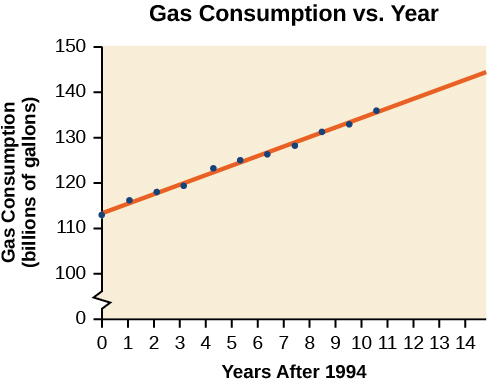
Podemos introduzir uma nova variável de entrada\(t\), representando anos desde 1994.

A equação de regressão de mínimos quadrados é:

\[C(t)=113.318+2.209t\]

Usando a tecnologia, o coeficiente de correlação foi calculado em 0,9965, sugerindo uma tendência linear crescente muito forte.

Usando isso para prever o consumo em 2008\((t=14)\),

\[\begin{align} C(14)&=113.318+2.209(14) \\ &=144.244 \end{align}\]

O modelo prevê 144,244 bilhões de galões de consumo de gasolina em 2008.

Exercício\(\PageIndex{1}\)

Use o modelo que criamos usando a tecnologia em Example\(\PageIndex{6}\) para prever o consumo de gás em 2011. Isso é uma interpolação ou uma extrapolação?

Responda

150,871 bilhões de galões; extrapolação

Conceitos-chave

• Os gráficos de dispersão mostram a relação entre dois conjuntos de dados.
• Os gráficos de dispersão podem representar modelos lineares ou não lineares.
• A linha de melhor ajuste pode ser estimada ou calculada, usando uma calculadora ou software estatístico.
• A interpolação pode ser usada para prever valores dentro do domínio e do intervalo dos dados, enquanto a extrapolação pode ser usada para prever valores fora do domínio e do intervalo dos dados.
• O coeficiente de correlação\(r\),, indica o grau de relação linear entre os dados.
• Uma linha de regressão se ajusta melhor aos dados.
• A linha de regressão de mínimos quadrados é encontrada minimizando os quadrados das distâncias dos pontos de uma linha que passa pelos dados e pode ser usada para fazer previsões sobre qualquer uma das variáveis.