1.R: Funções (Revisão)
- Page ID
- 189201
1.1: Funções e notação de funções
Para os exercícios 1-4, determine se a relação é uma função.
1)\(\{(a,b),(c,d),(e,d)\}\)
- Responda
-
função
2)\(\{(5,2),(6,1),(6,2),(4,8)\}\)
3)\(y^2+4=x\)
- Responda
-
não é uma função
4) O gráfico na Figura abaixo é uma função?
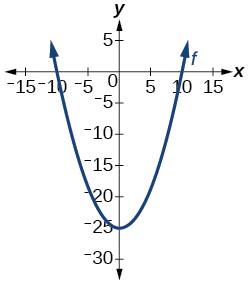
Para os exercícios 5-6, avalie a função nos valores indicados:\(f(-3); f(2); f(-a); -f(a); f(a+h)\)
5)\(f(x)=-2x^2+3x\)
- Responda
-
\(f(-3)=-27; f(2)=-2;f(-a)=-2a^2-3a;-f(a)=2a^2-3a;f(a+h)=-2a^2+3a-4ah+3h-2h^2\)
6)\(f(x)=2|3x-1|\)
Para os exercícios 7-8, determine se as funções são individuais.
7)\(f(x)=-3 x+5\)
- Responda
-
um para um
8)\(f(x)=|x-3|\)
Para os exercícios 9-11, use o teste de linha vertical para determinar se a relação cujo gráfico é fornecido é uma função.
9)
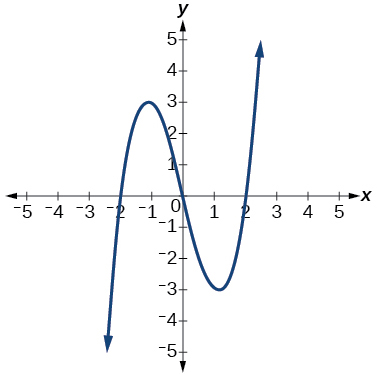
- Responda
-
função
10)
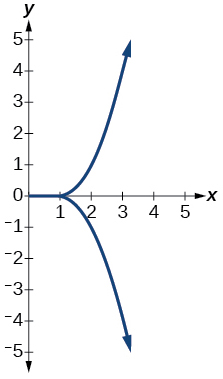
11)
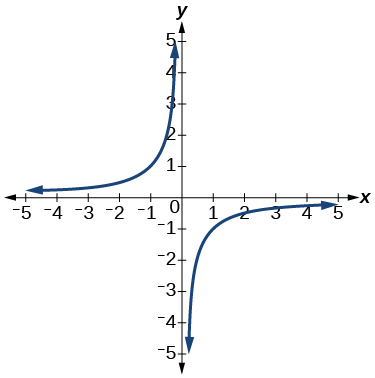
- Responda
-
função
Para os exercícios 12-13, faça um gráfico das funções.
12)\(f(x)=|x+1|\)
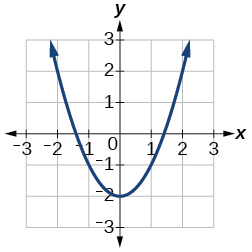
13)\(f(x)=x^{2}-2\)
- Responda
-
Para os exercícios 14-17, use a Figura abaixo para aproximar os valores.
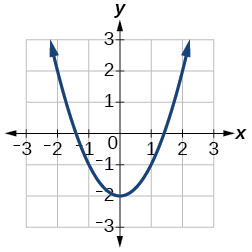
14)\(f(2)\)
15)\(f(-2)\)
- Responda
-
\(2\)
16) Se\(f(x)=-2\), então resolva para\(x\)
17) Se\(f(x)=1\), então resolva para\(x\)
- Responda
-
\(x=-1.8\)ou\(x=1.8\)
Para os exercícios 18-19, use a função\(h(t)=-16 t^{2}+80t\) para encontrar os valores.
18)\(\dfrac{h(2)-h(1)}{2-1}\)
19)\(\dfrac{h(a)-h(1)}{a-1}\)
- Responda
-
\(\dfrac{-64+80 a-16 a^{2}}{-1+a}=-16 a+64\)
1.2: Domínio e alcance
Para os exercícios 1-4, encontre o domínio de cada função, expressando as respostas usando a notação de intervalo.
1)\(f(x)=\dfrac{2}{3 x+2}\)
2)\(f(x)=\frac{x-3}{x^{2}-4 x-12}\)
- Responda
-
\((-\infty,-2) \cup(-2,6) \cup(6, \infty)\)
3)
4) Faça um gráfico desta função por partes:\(f(x)=\left\{\begin{array}{ll}{x+1} & {x<-2} \\ {-2 x-3} & {x \geq-2}\end{array}\right.\)
- Responda
-
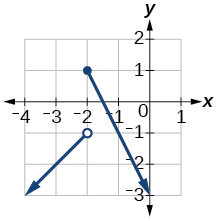
1.3: Taxas de mudança e comportamento dos gráficos
Para os exercícios 1-3, determine a taxa média de mudança das funções de\(x=1\) para\(x=2\)
1)\(f(x)=4 x-3\)
2)\(f(x)=10 x^{2}+x\)
- Responda
-
\(31\)
3)\(f(x)=-\dfrac{2}{x^{2}}\)
Para os exercícios 4-6, use os gráficos para determinar os intervalos nos quais as funções estão aumentando, diminuindo ou constantes.
4)
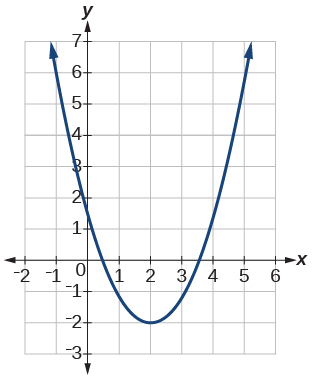
- Responda
-
aumentando\((2, \infty)\); diminuindo\((-\infty, 2)\)
5)
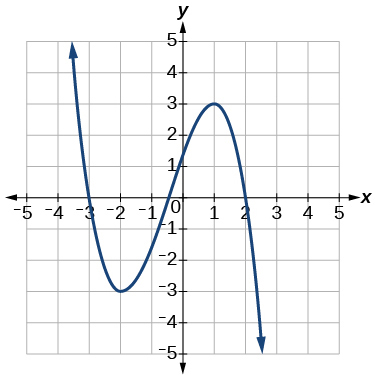
6)
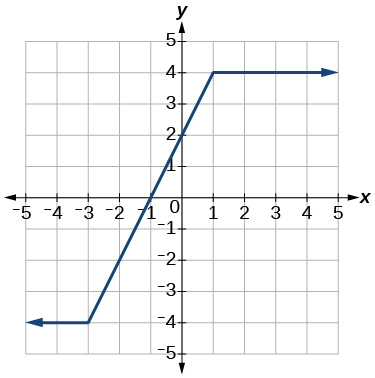
- Responda
-
aumentando\((-3,1)\); constante\((-\infty,-3) \cup(1, \infty)\)
7) Encontre o mínimo local da função representada graficamente no Exercício 4.
8) Encontre a extremidade local para a função representada graficamente no Exercício 5.
- Responda
-
mínimo local\((-2,-3)\); máximo local\((1,3)\)
9) Para o gráfico na Figura do Exercício 10, o domínio da função é\([-3,3]\). O alcance é\([-10,10]\). Encontre o mínimo absoluto da função nesse intervalo.
10) Encontre o máximo absoluto da função representada graficamente na Figura abaixo.
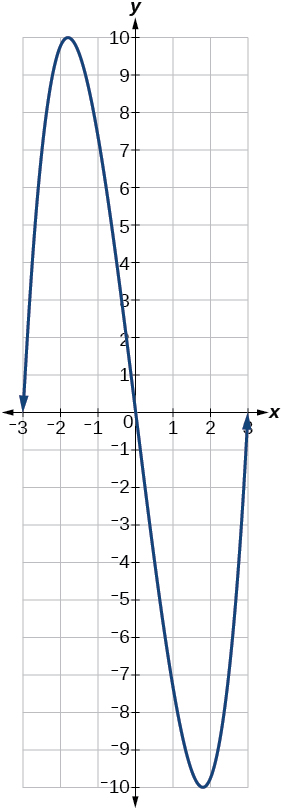
- Responda
-
\((-1.8,10)\)
1.4: Composição das funções
Para os exercícios 1-5, encontre\((f \circ g)(x)\) e\((g \circ f)(x)\) para cada par de funções.
1)\(f(x)=4-x, g(x)=-4x\)
2)\(f(x)=3 x+2, g(x)=5-6x\)
- Responda
-
\((f \circ g)(x)=17-18 x ;(g \circ f)(x)=-7-18x\)
3)\(f(x)=x^{2}+2 x, g(x)=5 x+1\)
4)\(f(x)=\sqrt{x+2}, g(x)=\dfrac{1}{x}\)
- Responda
-
\((f \circ g)(x)=\sqrt{\dfrac{1}{x}+2} ;(g \circ f)(x)=\dfrac{1}{\sqrt{x+2}}\)
5)\(f(x)=\dfrac{x+3}{2}, g(x)=\sqrt{1-x}\)
Para os exercícios 6-9, encontre\((f \circ g)\) e o domínio\((f \circ g)(x)\) para cada par de funções.
6)\(f(x)=\frac{x+1}{x+4}, g(x)=\frac{1}{x}\)
- Responda
-
\((f \circ g)(x)=\dfrac{1+x}{1+4 x}, x \neq 0, x \neq-\dfrac{1}{4}\)
7)\(f(x)=\dfrac{1}{x+3}, g(x)=\dfrac{1}{x-9}\)
8)\(f(x)=\dfrac{1}{x}, g(x)=\sqrt{x}\)
- Responda
-
\((f \circ g)(x)=\frac{1}{\sqrt{x}}, x>0\)
9)\(f(x)=\frac{1}{x^{2}-1}, g(x)=\sqrt{x+1}\)
Para os exercícios 10-11, expresse cada função\(H\) como uma composição de duas funções\(f\) e\(g\) onde\(H(x)=(f \circ g)(x)\)
10)\(H(x)=\sqrt{\frac{2 x-1}{3 x+4}}\)
- Responda
-
amostra:\(g(x)=\dfrac{2 x-1}{3 x+4}; f(x)=\sqrt{x}\)
11)\(H(x)=\dfrac{1}{\left(3 x^{2}-4\right)^{-3}}\)
1.5: Transformação de funções
Para os exercícios 1-8, esboce um gráfico da função dada.
1)\(f(x)=(x-3)^{2}\)
- Responda
-
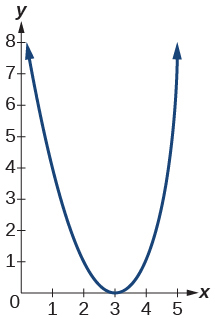
2)\(f(x)=(x+4)^{3}\)
3)\(f(x)=\sqrt{x}+5\)
- Responda
-
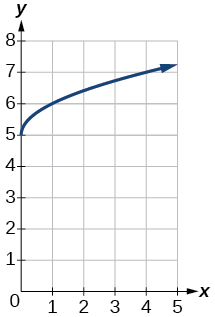
4)\(f(x)=-x^{3}\)
5)\(f(x)=\sqrt[3]{-x}\)
- Responda
-
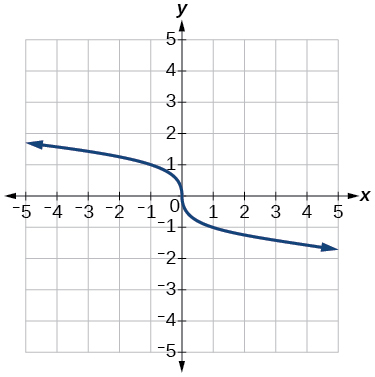
6)\(f(x)=5 \sqrt{-x}-4\)
7)\(f(x)=4[|x-2|-6]\)
- Responda
-
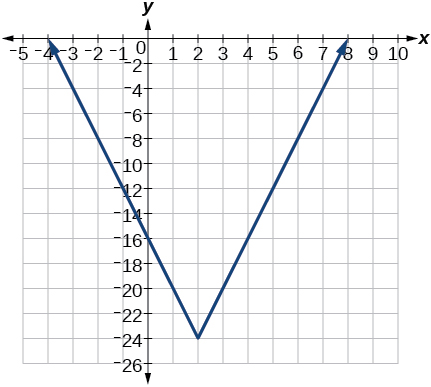
8)\(f(x)=-(x+2)^{2}-1\)
Para os exercícios 9-10, esboce o gráfico da função\(g\) se o gráfico da função\(f\) for mostrado na Figura abaixo.
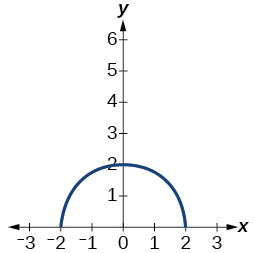
9)\(g(x)=f(x-1)\)
- Responda
-
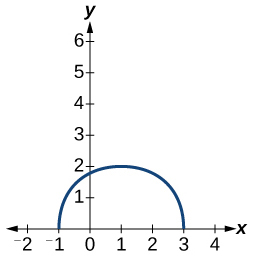
10)\(g(x)=3 f(x)\)
Para os exercícios 11-12, escreva a equação para a função padrão representada por cada um dos gráficos abaixo.
11)
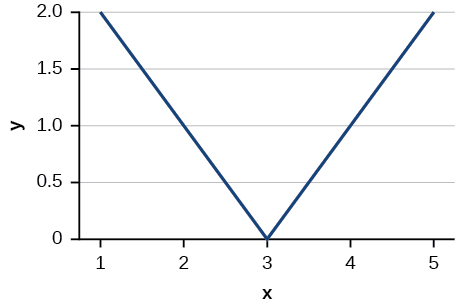
- Responda
-
\(f(x)=|x-3|\)
12)
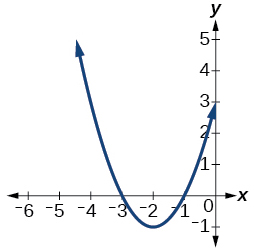
Para os exercícios 13-15, determine se cada função abaixo é par, ímpar ou nenhuma.
13)\(f(x)=3 x^{4}\)
- Responda
-
uniforme
14)\(g(x)=\sqrt{x}\)
15)\(h(x)=\frac{1}{x}+3 x\)
- Responda
-
estranha
Para os exercícios 16-18, analise o gráfico e determine se a função gráfica é par, ímpar ou nenhuma.
16)
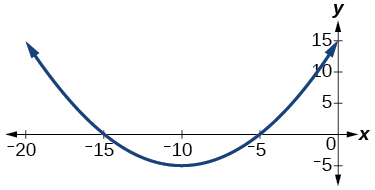
17)
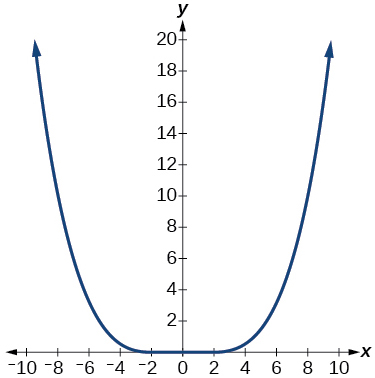
- Responda
-
uniforme
18)
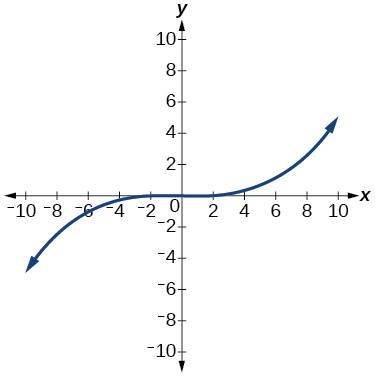
1.6: Funções de valor absoluto
Para os exercícios 1-3, escreva uma equação para a transformação de\(f(x)=|x|\).
1)
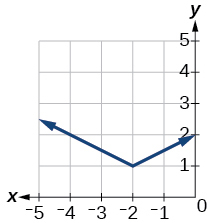
- Responda
-
\(f(x)=\dfrac{1}{2}|x+2|+1\)
2)
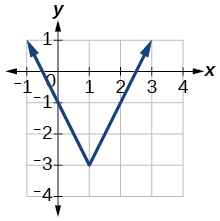
3)
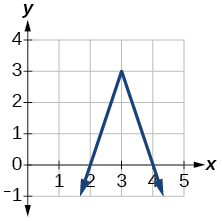
- Responda
-
\(f(x)=-3|x-3|+3\)
Para os exercícios 4-6, represente graficamente a função de valor absoluto.
4)\(f(x)=|x-5|\)
5)\(f(x)=-|x-3|\)
- Responda
-
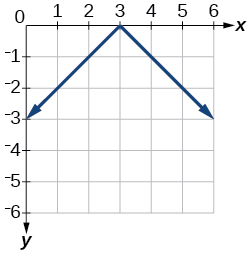
6)\(f(x)=|2 x-4|\)
Para os exercícios 7-8, resolva a equação do valor absoluto.
7)\(|x+4|=18\)
- Responda
-
\(x=-22, x=14\)
8)\(\left|\dfrac{1}{3} x+5\right|=\left|\dfrac{3}{4} x-2\right|\)
Para os exercícios 9-10, resolva a desigualdade e expresse a solução usando a notação de intervalo.
9)\(|3 x-2|<7\)
- Responda
-
\(\left(-\dfrac{5}{3}, 3\right)\)
10)\(\left|\dfrac{1}{3} x-2\right| \leq 7\)
1.7: Funções inversas
Para os exercícios 1-2, encontre\(f^{-1}(x)\) para cada função.
1)\(f(x)=9+10 x\)
2)\(f(x)=\dfrac{x}{x+2}\)
- Responda
-
\(f^{-1}(x)=\dfrac{-2 x}{x-1}\)
3) Para o exercício a seguir, encontre um domínio no qual a função\(f\) seja individual e não decrescente. Escreva o domínio em notação de intervalo. Em seguida, encontre o inverso de\(f\) restrito a esse domínio. \[f(x)=x^{2}+1\]
4) Dado\(f(x)=x^{3}-5\) e\(g(x)=\sqrt[3]{x+5} \):
- Encontre\(f(g(x))\)\(g(f(x))\) e.
- O que a resposta nos diz sobre a relação entre\(f(x)\) e\(g(x) ?\)
- Responda
-
- \(f(g(x))=x\)e\(g(f(x))=x\)
- Isso nos diz que\(f\) e\(g\) são funções inversas
Para os exercícios 5-8, use um utilitário gráfico para determinar se cada função é individual.
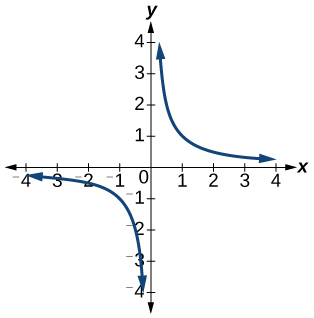
5)\(f(x)=\dfrac{1}{x}\)
- Responda
-
A função é individual.
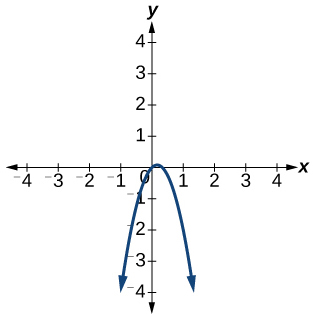
6)\(f(x)=-3 x^{2}+x\)
- Responda
-
A função não é individual.
7) Se\(f(5)=2,\) encontrar\(f^{-1}(2)\)
- Responda
-
\(5\)
8) Se\(f(1)=4,\) encontrar\(f^{-1}(4)\)
Teste prático
Para os exercícios 1-2, determine se cada uma das relações a seguir é uma função.
1)\(y=2 x+8\)
- Responda
-
A relação é uma função.
2)\(\{(2,1),(3,2),(-1,1),(0,-2)\}\)
Para os exercícios 3-4, avalie a função\(f(x)=-3 x^{2}+2 x\) na entrada fornecida.
3)\(f(-2)\)
- Responda
-
\(-16\)
4)\(f(a)\)
5) Mostre que a função não\(f(x)=-2(x-1)^{2}+3\) é individual.
- Responda
-
O gráfico é uma parábola e o gráfico falha no teste da linha horizontal.
6) Escreva o domínio da função\(f(x)=\sqrt{3-x}\) em notação de intervalo.
7) Dado o\(f(x)=2 x^{2}-5 x,\) achado\(f(a+1)-f(1)\)
- Responda
-
\(2 a^{2}-a\)
8) Representar graficamente a função\(f(x)=\left\{\begin{array}{ccc}{x+1} & {\text { if }} & {-2<x<3} \\ {-x} & {\text { if }} & {x \geq 3}\end{array}\right.\)
9) Encontre a taxa média de variação da função\(f(x)=3-2 x^{2}+x\) encontrando\(\dfrac{f(b)-f(a)}{b-a}\)
- Responda
-
\(-2(a+b)+1\)
Para os exercícios 10-11, use as funções\(f(x)=3-2 x^{2}+x\) e\(g(x)=\sqrt{x}\) encontre as funções compostas.
10)\((g \circ f)(x)\)
11)\((g \circ f)(1)\)
- Responda
-
\(\sqrt{2}\)
12) Expresse\(H(x)=\sqrt[3]{5 x^{2}-3 x}\) uma composição de duas funções\(f\) e\(g,\) onde\((f \circ g)(x)=H(x)\)
Para os exercícios 13-14, represente graficamente as funções traduzindo, esticando e/ou comprimindo uma função do kit de ferramentas.
13)\(f(x)=\sqrt{x+6}-1\)
- Responda
-
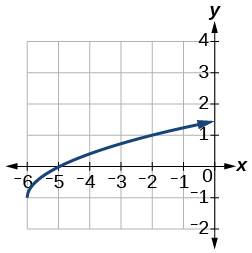
14)\(f(x)=\dfrac{1}{x+2}-1\)
Para os exercícios 15-17, determine se as funções são pares, ímpares ou inexistentes.
15)\(f(x)=-\dfrac{5}{x^{2}}+9 x^{6}\)
- Responda
-
uniforme
16)\(f(x)=-\dfrac{5}{x^{3}}+9 x^{5}\)
17)\(f(x)=\dfrac{1}{x}\)
- Responda
-
estranha
18) Faça um gráfico da função de valor absoluto\(f(x)=-2|x-1|+3\).
19) Resolver\(|2 x-3|=17\).
- Responda
-
\(x=-7\)e\(x=10\)
20) Resolver\(-\left|\dfrac{1}{3} x-3\right| \geq 17\). Expresse a solução em notação de intervalo.
Para os exercícios 21-22, determine o inverso da função.
21)\(f(x)=3 x-5\)
- Responda
-
\(f^{-1}(x)=\dfrac{x+5}{3}\)
22)\(f(x)=\dfrac{4}{x+7}\)
Para os exercícios 23-26, use o gráfico\(g\) mostrado na Figura abaixo.
23) Em quais intervalos a função está aumentando?
- Responda
-
\((-\infty,-1.1)\)e\((1.1, \infty)\)
24) Em quais intervalos a função está diminuindo?
25) Aproxime o mínimo local da função. Expresse a resposta como um par ordenado.
- Responda
-
\((1.1,-0.9)\)
26) Aproxime o máximo local da função. Expresse a resposta como um par ordenado.
Para os exercícios 27-29, use o gráfico da função por partes mostrado na Figura abaixo.
27) Encontrar\(f(2)\).
- Responda
-
\(f(2)=2\)
28) Encontre\(f(-2)\).
29) Escreva uma equação para a função por partes.
- Responda
-
\(f(x)=\left\{\begin{array}{cl}{|x|} & {\text { if } x \leq 2} \\ {3} & {\text { if } x>2}\end{array}\right.\)
Para os exercícios 30-35, use os valores listados na Tabela abaixo.
| \(x\) | \(F(x)\) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
| 6 | 13 |
| 7 | 15 |
| 8 | 17 |
30) Encontre\(F(6)\).
31) Resolva a equação\(F(x)=5\)
- Responda
-
\(x=2\)
32) O gráfico está aumentando ou diminuindo em seu domínio?
33) A função é representada pelo gráfico um a um?
- Responda
-
sim
34) Encontrar\(F^{-1}(15)\).
35) Dado o\(f(x)=-2 x+11,\) achado\(f^{-1}(x)\).
- Responda
-
\(f^{-1}(x)=-\dfrac{x-11}{2}\)


