1.E: Funções (exercícios)

1.1: Funções e notação de funções

Um avião a jato muda de altitude à medida que sua distância do ponto de partida de um voo aumenta. O peso de uma criança em crescimento aumenta com o tempo. Em cada caso, uma quantidade depende da outra. Há uma relação entre as duas quantidades que podemos descrever, analisar e usar para fazer previsões. Nesta seção, analisaremos essas relações.

Verbal

1) Qual é a diferença entre uma relação e uma função?

Responda

Uma relação é um conjunto de pares ordenados. Uma função é um tipo especial de relação em que dois pares ordenados não têm a mesma primeira coordenada.

2) Qual é a diferença entre a entrada e a saída de uma função?

3) Por que o teste de linha vertical nos diz se o gráfico de uma relação representa uma função?

Responda

Quando uma linha vertical cruza o gráfico de uma relação mais de uma vez, isso indica que para essa entrada há mais de uma saída. Em qualquer valor de entrada específico, só pode haver uma saída se a relação for uma função.

4) Como você pode determinar se uma relação é uma função individual?

5) Por que o teste de linha horizontal nos diz se o gráfico de uma função é um para um?

Responda

Quando uma linha horizontal cruza o gráfico de uma função mais de uma vez, isso indica que para essa saída há mais de uma entrada. Uma função é individual se cada saída corresponder a apenas uma entrada.

Algébrico

Para os exercícios 6-7, determine se a relação representa uma função.

6)$\{(a,b), (c,d), (a,c)\}$

7)$\{(a,b),(b,c),(c,c)\}$

Responda

função

Para os exercícios 8-26, determine se a relação representa$y$ em função de$x$.

8)$5x+2y=10$

9)$y=x^2$

Responda

função

10)$x=y^2$

11)$3x^2+y=14$

Responda

função

12)$2x+y^2=6$

13)$y=−2x^2+40x$

Responda

função

14)$y=\dfrac{1}{x}$

15)$x=\dfrac{3y+5}{7y−1}$

Responda

função

16)$x=\sqrt{1−y^2}$

17)$y=\dfrac{3x+5}{7x−1}$

Responda

função

18)$x^2+y^2=9$

19)$2xy=1$

Responda

função

20)$x=y^3$

21)$y=x^3$

Responda

função

22)$y=\sqrt{1−x^2}$

23)$x=\pm\sqrt{1-y}$

Responda

função

24)$y=\pm\sqrt{1−x}$

25)$y^2=x^2$

Responda

não é uma função

26)$y^3=x^2$

Para os exercícios 27-39, avalie a função$f$ nos valores indicados$f(−3),f(2),f(−a),−f(a),f(a+h)$.

27)$f(x)=2x−5$

Responda

$f(−3)=−11$;$f(2)=−1$;$f(−a)=−2a−5$;$−f(a)=−2a+5$;$f(a+h)=2a+2h−5$

28)$f(x)=−5x^2+2x−1$

29)$f(x)=\sqrt{2−x}+5$

Responda

$f(−3)=\sqrt{5+5}$;$f(2)=5$;$f(−a)=\sqrt{2+a+5}$;$−f(a)=−\sqrt{2−a}−5$;$f(a+h)=\sqrt{2−a−h}+5$

30)$f(x)=\dfrac{6x−1}{5x+2}$

31)$f(x)=|x−1|−|x+1|$

Responda

$f(−3)=2$;$f(2)=1−3=−2$;$f(−a)=|−a−1|−|−a+1|$;$−f(a)=−|a−1| +|a+1|$;$f(a+h)= |a+h−1|−|a+h+1|$

32) Dada a função$g(x)=5−x^2$,$g(x+h)−g(x)h$ avalie,$h{\neq}0$.

33) Dada a função$g(x)=x^2+2x$,$\dfrac{g(x)−g(a)}{x−a}$ avalie,$x{\neq}a$.

Responda

$\dfrac{g(x)−g(a)}{x−a}=x+a+2$,$x{\neq}a$

34) Dada a função$k(t)=2t−1$:

a. Avalie$k(2)$.
b. Resolver$k(t)=7$.

35) Dada a função$f(x)=8−3x$:

a. Avalie$f(−2)$.
b. Resolver$f(x)=−1$.

Responda

a.$f(−2)=14$; b.$x=3$

36) Dada a função$p(c)=c^2+c$:

a. Avalie$p(−3)$.
b. Resolver$p(c)=2$.

37) Dada a função$f(x)=x^2−3x$:

a. Avalie$f(5)$.
b. Resolver$f(x)=4$.

Responda

a.$f(5)=10$; b.$x=−1$ ou$x=4$

38) Dada a função$f(x)=\sqrt{x+2}$:

a. Avalie$f(7)$.
b. Resolver$f(x)=4$.

39) Considere o relacionamento$3r+2t=18$.

a. Escreva o relacionamento como uma função$r=f(t)$.
b. Avalie$f(−3)$.
c. Resolver$f(t)=2$.

Responda

a.$f(t)=6−\frac{2}{3}t$; b.$f(−3)=8$; c.$t=6$

Gráfica

Para os exercícios 40-54, use o teste de linha vertical para determinar quais gráficos mostram relações que são funções.

40)

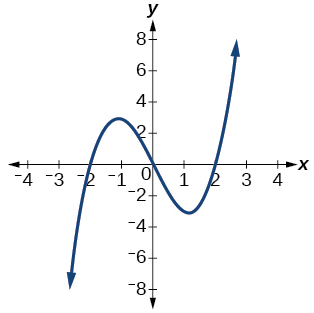
41)

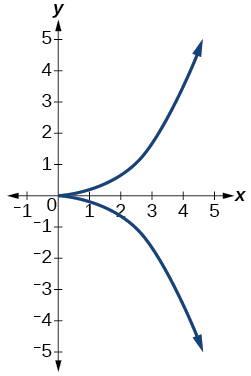
Responda

não é uma função

(42)

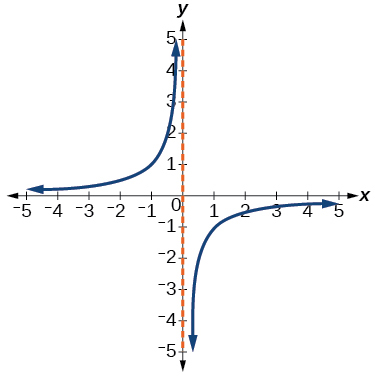
43)

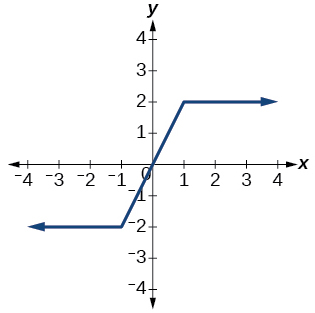
Responda

função

44)

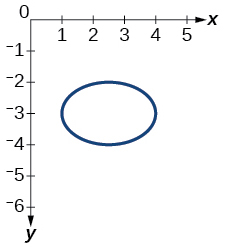
45)

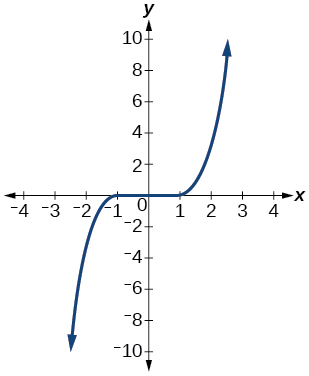
Responda

função

(46)

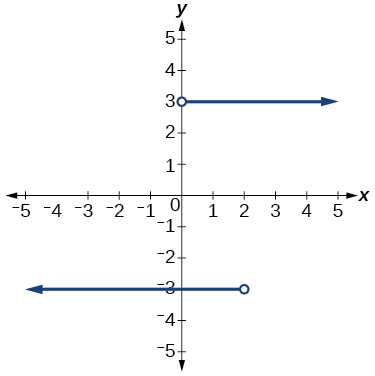
47)

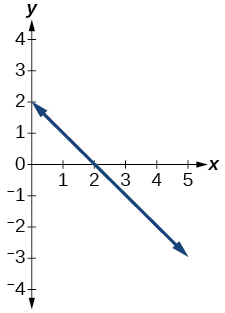
Responda

função

48)

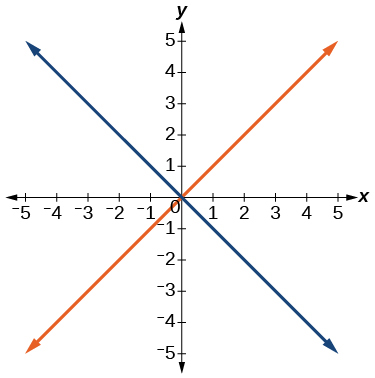
49)

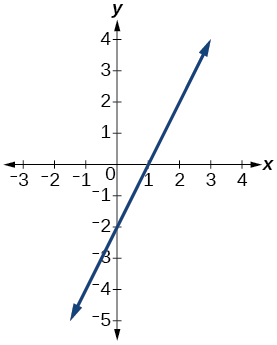
Responda

função

50)

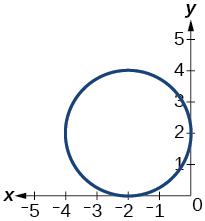
51)

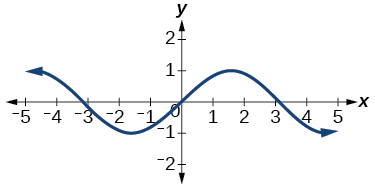
Responda

função

52) Dado o gráfico a seguir,

• Avalie$f(−1)$.
• Resolva para$f(x)=3$.

53) Dado o gráfico a seguir,

• Avalie$f(0)$.
• Resolva para$f(x)=−3$.

Responda

a.$f(0)=1$; b.$f(x)=−3$,$x=−2$ ou$x=2$

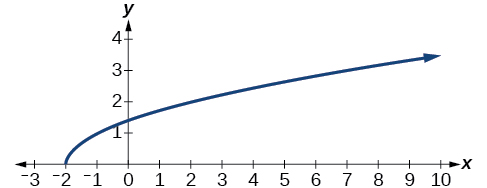
54) Dado o gráfico a seguir,

• Avalie$f(4)$.
• Resolva para$f(x)=1$.

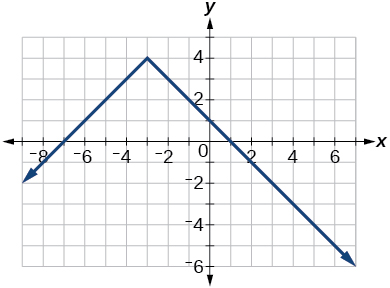
Para os exercícios 55-59, determine se o gráfico fornecido é uma função individual.

55)

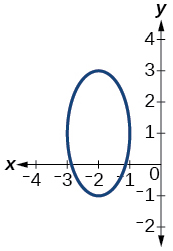
Responda

não é uma função, então também não é uma função individual

56)

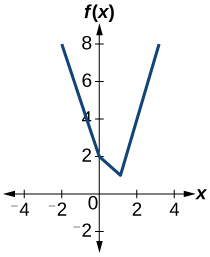
57)

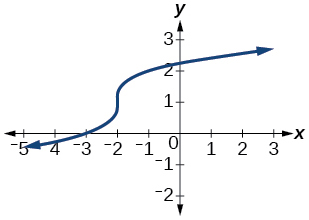
Responda

função um para um

(58)

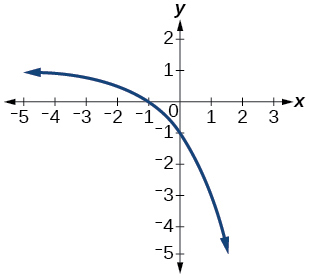
(59)

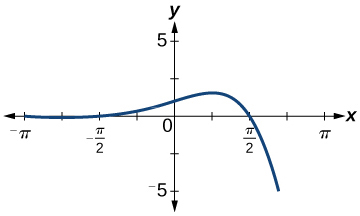
Responda

função, mas não uma para uma

Numérico

Para os exercícios 60-62, determine se a relação representa uma função.

60)$\{(−1,−1),(−2,−2),(−3,−3)\}$

61)$\{(3,4),(4,5),(5,6)\}$

Responda

função

62)$(2,5),(7,11),(15,8),(7,9)\}$

Para os exercícios 63-65, determine se a relação representada em forma de tabela representa$y$ em função de$x$.

63)

$x$	5	10	15
$y$	3	8	14

Responda

função

64)

$x$	5	10	15
$y$	3	8	8

65)

$x$	5	10	10
$y$	3	8	14

Responda

não é uma função

Para os exercícios 66-67, use a função$f$ representada na Tabela abaixo

$x$	$f(x)$
\ (x\) ">0	\ (f (x)\) ">74
\ (x\) ">1	\ (f (x)\) ">28
\ (x\) ">2	\ (f (x)\) ">1
\ (x\) ">3	\ (f (x)\) ">53
\ (x\) ">4	\ (f (x)\) ">56
\ (x\) ">5	\ (f (x)\) ">3
\ (x\) ">6	\ (f (x)\) ">36
\ (x\) ">7	\ (f (x)\) ">45
\ (x\) ">8	\ (f (x)\) ">14
\ (x\) ">9	\ (f (x)\) ">47

66) Avalie$f(3)$.

67) Resolver$f(x)=1$.

Responda

$f(x)=1$,$x=2$

Para os exercícios 68-73, avalie$f$ a função nos valores$f(−2)$$f(−1)$$f(0)$,$f(1)$,,$f(2)$ e.

68)$f(x)=4−2x$

69)$f(x)=8−3x$

Responda

$f(−2)=14$;$f(−1)=11$;$f(0)=8$;$f(1)=5$;$f(2)=2$

70)$f(x)=8x^2−7x+3$

71)$f(x)=3+\sqrt{x+3}$

Responda

$f(−2)=4$;$f(−1)=4.414$;$f(0)=4.732$;$f(1)=4.5$;$f(2)=5.236$

72)$f(x)=\dfrac{x-2}{x+3}$

73)$f(x)=3^x$

Responda

$f(−2)=\frac{1}{9}$;$f(−1)=\frac{1}{3}$;$f(0)=1$;$f(1)=3$;$f(2)=9$

Para os exercícios 74-75, avalie as expressões$f$$g$, determinadas funções e$h$:

• $f(x)=3x−2$
• $g(x)=5−x^2$
• $h(x)=−2x^2+3x−1$

74)$3f(1)−4g(−2)$

75)$f \left (\dfrac{7}{3} \right )−h(−2)$

Responda

$20$

Tecnologia

Para os exercícios 76-78, faça um gráfico$y=x^2$ na janela de visualização fornecida. Determine a faixa correspondente para cada janela de visualização. Mostre cada gráfico.

76)$[−0.1, 0.1]$

77)$[−10, 10]$

Responda

$[0, 100]$

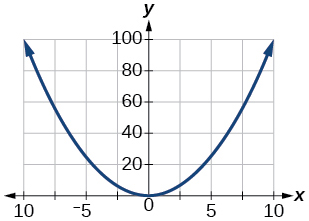
78)$[−100,100]$

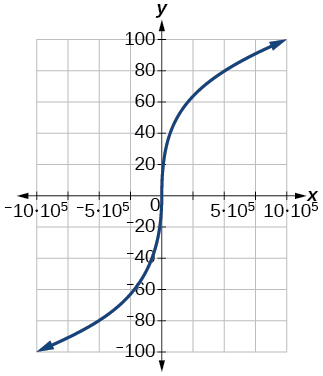
Para os exercícios 79-81, faça um gráfico$y=x^3$ na janela de visualização fornecida. Determine a faixa correspondente para cada janela de visualização. Mostre cada gráfico.

79)$[−0.1, 0.1]$

Responda

$[−0.001, 0.001]$

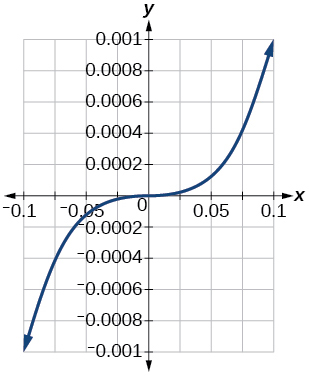
80)$[−10, 10]$

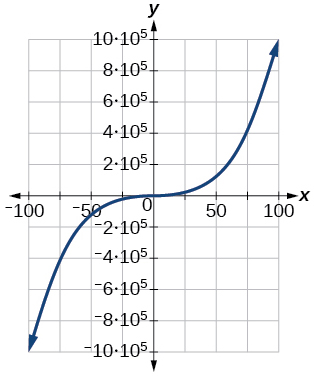
81)$[−100, 100]$

Responda

$[−1,000,000, 1,000,000]$

Para os exercícios 82-84, faça um gráfico$y=\sqrt{x}$ na janela de visualização fornecida. Determine a faixa correspondente para cada janela de visualização. Mostre cada gráfico.

82)$[0, 0.01]$

83)$[0, 100]$

Responda

$[0, 10]$

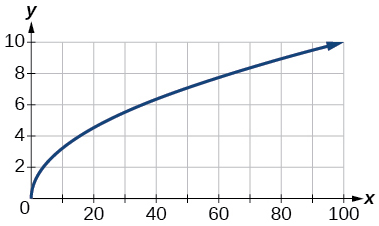
84)$[0, 10,000]$

Para os exercícios 85-87, faça um gráfico$y=\sqrt[3]{x}$ na janela de visualização fornecida. Determine a faixa correspondente para cada janela de visualização. Mostre cada gráfico.

85)$[−0.001,0.001]$

Responda

$[−0.1,0.1]$

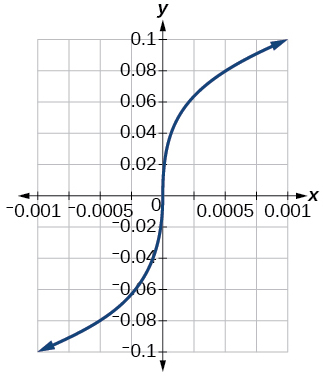
86)$[−1000,1000]$

87)$[−1,000,000,1,000,000]$

Responda

$[−100, 100]$

Aplicativos do mundo real

88) A quantidade de lixo$G$, produzida por uma cidade com população$p$ é dada por$G=f(p)$. $G$é medido em toneladas por semana e$p$ é medido em milhares de pessoas.

A cidade de Tola tem uma população de$40,000$ e produz$13$ toneladas de lixo a cada semana. Expresse essas informações em termos da função$f$. Tola tem uma população de$40,000$ e produz$13$ toneladas de lixo a cada semana. Expresse essas informações em termos da função$f$.
Explique o significado da declaração$f(5)=2$.

89) O número de metros cúbicos de terra$D$, necessários para cobrir um jardim com área de um metro quadrado é dado por$D=g(a)$.

a. Um jardim com área$5000$$ft^2$ requer$50$$yd^3$ sujeira. Expresse essas informações em termos da função$g$.
b. Explique o significado da declaração$g(100)=1$.

Responda

a.$g(5000)=50$; b. O número de metros cúbicos de terra necessários para um jardim de pés$100$ quadrados é$1$.

90)$f(t)$ Seja o número de patos em um lago$t$ anos após 1990. Explique o significado de cada declaração:

a. f (5) =30
b. f (10) =40

91)$h(t)$ Seja a altura acima do solo, em pés, de um foguete$t$ segundos após o lançamento. Explique o significado de cada declaração:

a.$h(1)=200$
b.$h(2)=350$

Responda

a. A altura de um foguete acima do solo após o$1$ segundo é$200$ ft. b. a altura de um foguete acima do solo após$2$ segundos é$350$ ft.

92) Mostre que a função não$f(x)=3(x−5)^2+7$ é individual.

1.2: Domínio e alcance

Ao criar várias funções usando os dados, podemos identificar diferentes variáveis independentes e dependentes e analisar os dados e as funções para determinar o domínio e o intervalo. Nesta seção, investigaremos métodos para determinar o domínio e a variedade de funções.

Verbal

1) Por que o domínio é diferente para diferentes funções?

Responda

O domínio de uma função depende de quais valores da variável independente tornam a função indefinida ou imaginária.

2) Como determinamos o domínio de uma função definida por uma equação?

3) Explique por que o domínio de$f(x)=\sqrt[3]{x}$ é diferente do domínio de$f(x)=\sqrt{x}$.

Responda

Não há restrição de x$f(x)=\sqrt[3]{x}$ porque você pode obter a raiz cúbica de qualquer número real. Portanto, o domínio é todo em números reais,$(−∞,∞)$. Ao lidar com o conjunto de números reais, você não pode usar a raiz quadrada dos números negativos. Portanto, os valores de x são restritos$f(x)=\sqrt{x}$ a números não negativos e o domínio é$[0,∞)$.

4) Ao descrever conjuntos de números usando notação de intervalo, quando você usa um parêntese e quando usa um colchete?

5) Como você representa graficamente uma função por partes?

Responda

Faça um gráfico de cada fórmula da função por partes sobre seu domínio correspondente. Use a mesma escala para o eixo x e o eixo y para cada gráfico. Indique pontos finais inclusivos com um círculo sólido e pontos finais exclusivos com um círculo aberto. Use uma seta para indicar$−∞$ ou$∞$. Combine os gráficos para encontrar o gráfico da função por partes.

Algébrico

Para os exercícios 6-25, encontre o domínio de cada função usando a notação de intervalo.

6)$f(x)=−2x(x−1)(x−2)$

7)$f(x)=5−2x^2$

Responda

$(-\infty,\infty)$

8)$f(x)=3\sqrt{x-2}$

9)$f(x)=3-\sqrt{6-2x}$

Responda

$\left(-\infty,3\right]$

10)$f(x)=\sqrt{4-3x}$

11)$f(x)=\sqrt{x^2+4}$

Responda

$(-\infty,\infty)$

12)$f(x)=\sqrt[3]{1-2x}$

13)$f(x)=\sqrt[3]{x-1}$

Responda

$(-\infty,\infty)$

14)$f(x)=\dfrac{9}{x-6}$

15)$f(x)=\dfrac{3x+1}{4x+2}$

Responda

$\left (-\infty,-\dfrac{1}{2} \right )\cup \left (-\dfrac{1}{2},\infty \right )$

16)$f(x)=\dfrac{\sqrt{x+4}}{x-4}$

17)$f(x)=\dfrac{x-3}{x^2+9x-22}$

Responda

$(-\infty,-11)\cup(-11,2)\cup(2,\infty)$

18)$f(x)=\dfrac{1}{x^2-x-6}$

19)$f(x)=\dfrac{2x^3−250}{x^2−2x−15}$

Responda

$(-\infty,-3)\cup(-3,5)\cup(5,\infty)$

20)$\dfrac{5}{\sqrt{x-3}}$

21)$\dfrac{2x+1}{\sqrt{5-x}}$

Responda

$(-\infty,5)$

22)$\dfrac{\sqrt{x-4}}{\sqrt{x-6}}$

23)$\dfrac{\sqrt{x-6}}{\sqrt{x-4}}$

Responda

$\left[6,\infty\right)$

24)$f(x)=\dfrac{x}{x}$

25)$f(x)=\dfrac{x^2-9x}{x^2-81}$

Responda

$(-\infty,-9)\cup(-9,9)\cup(9,\infty)$

26) Encontre o domínio da função da$f(x)=\sqrt{2x^3-50x}$ seguinte forma:

a. usando álgebra

b. representando graficamente a função no radicando e determinando intervalos no eixo x para os quais o radicando não é negativo.

Gráfica

Para os exercícios 27-37, escreva o domínio e o intervalo de cada função usando a notação de intervalo.

27)

\ (\ left (2, 8\ right]\).” style="cor de fundo: transparente; cor da borda inferior: rgb (0, 0, 0); estilo da borda inferior: nenhum; largura da borda inferior: 0px; borda da imagem inicial: 0; border-image-repeat: stretch; border-image-slice: 100%; borda da imagem fonte da imagem: nenhuma; largura da borda da imagem: 1; cor da borda esquerda: rgb ( 0, 0, 0); estilo borda esquerda: nenhum; largura da borda esquerda: 0px; borda da cor da direita: rgb (0, 0, 0); estilo borda direita: nenhum; largura da borda direita: 0px; cor da borda superior: rgb (0, 0, 0); estilo borda superior: nenhum; largura da borda superior: 0px; cor: r gb (0, 0, 0); cursor: padrão; família da fonte: lato, arial, helvetica, sans-serif, & quot; arial unicode ms”; tamanho da fonte: 16px; estilo da fonte: normal; variante da fonte: normal; peso da fonte: 400; altura: 200px; espaçamento entre letras: normal; largura máxima: 1224px; opacidade: 0,8; órfãos: 2; alinhamento de texto: centro; decoração de texto: nenhum; recuo de texto: 0px; transformação de texto: nenhum; -web-transformação largura do traçado de texto do kit: 0px; branco -espaço: normal; largura: 200px; espaçamento entre palavras: 0px;” width="200px” height="200px” src=” https://math.libretexts.org/@api/dek..._01_02_202.jpg "/>

Responda

domínio:$\left(2,8\right]$, intervalo$\left[6,8\right)$

28)

\ (\ left [4, 8\ right)\).” style="cor de fundo: transparente; cor da borda inferior: rgb (0, 0, 0); estilo da borda inferior: nenhum; largura da borda inferior: 0px; borda da imagem inicial: 0; border-image-repeat: stretch; border-image-slice: 100%; borda da imagem fonte da imagem: nenhuma; largura da borda da imagem: 1; cor da borda esquerda: rgb ( 0, 0, 0); estilo borda esquerda: nenhum; largura da borda esquerda: 0px; borda da cor da direita: rgb (0, 0, 0); estilo borda direita: nenhum; largura da borda direita: 0px; cor da borda superior: rgb (0, 0, 0); estilo borda superior: nenhum; largura da borda superior: 0px; cor: r gb (0, 0, 0); cursor: padrão; família da fonte: lato, arial, helvetica, sans-serif, & quot; arial unicode ms”; tamanho da fonte: 16px; estilo da fonte: normal; variante da fonte: normal; peso da fonte: 400; altura: 200px; espaçamento entre letras: normal; largura máxima: 1224px; opacidade: 0,8; órfãos: 2; alinhamento de texto: centro; decoração de texto: nenhum; recuo de texto: 0px; transformação de texto: nenhum; -web-transformação largura do traçado de texto do kit: 0px; branco -espaço: normal; largura: 200px; espaçamento entre palavras: 0px;” width="200px” height="200px” src=” https://math.libretexts.org/@api/dek..._01_02_203.jpg "/>

29)

Responda

domínio:$[−4, 4]$, intervalo:$[0, 2]$

30)

31)

Responda

domínio:$\left[−5, 3\right)$, intervalo:$[0,2]$

32)

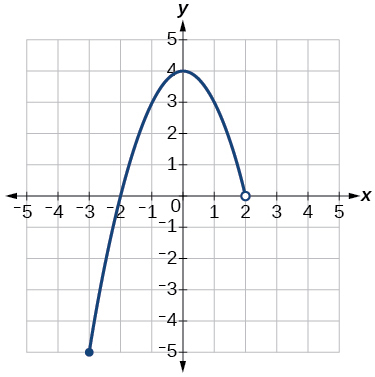
33)

Responda

domínio:$\left(−\infty,1\right]$, intervalo:$\left[0,\infty\right)$

34)

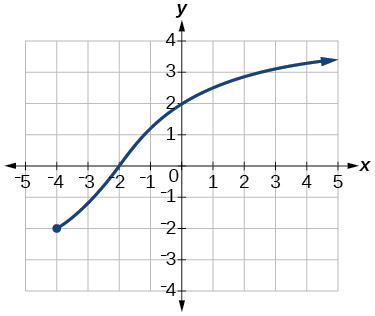
(35)

Responda

domínio:$[−6,−16]\cup[16,6]$; intervalo:$[−6,−16]\cup[16,6]$

36)

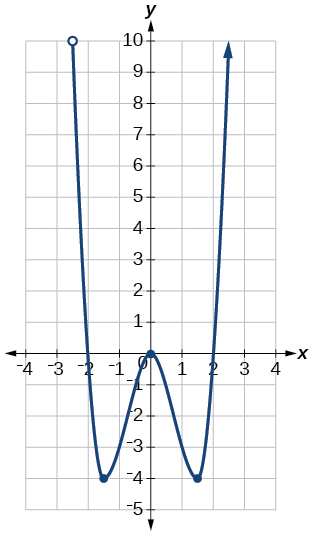
37)

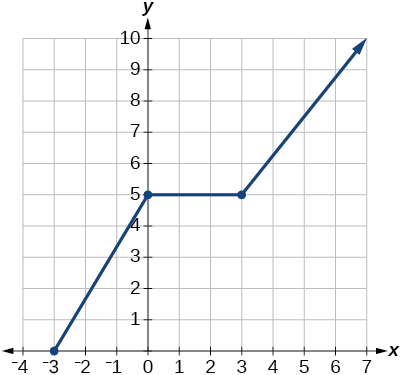
Responda

domínio:$\left[−3, \infty\right)$; intervalo:$\left[0,\infty\right)$

Para os exercícios 38-45, esboce um gráfico da função por partes. Escreva o domínio em notação de intervalo.

38)$f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}$

39)$f(x)= \begin{cases} 2x-1 & \text{if $x < 1$} \\ 1+x & \text{if $x {\geq} 1$} \end{cases}$

Responda

domínio:$(−\infty,\infty)$

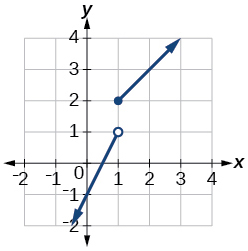
40)$f(x)= \begin{cases} x+1 & \text{if $x < 0$} \\ x-1 & \text{if $x > 0$} \end{cases}$

41)$f(x)= \begin{cases} 3 & \text{if $x < 0$} \\ \sqrt{x} & \text{if $x {\geq} 0$} \end{cases}$

Responda

domínio:$(−\infty,\infty)$

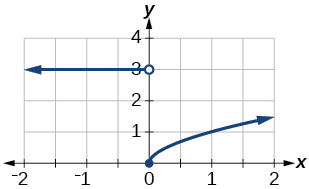
42)$f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ 1-x & \text{if $x > 0$} \end{cases}$

43)$f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ x+2 & \text{if $x {\geq} 0$} \end{cases}$

Responda

domínio:$(−\infty,\infty)$

44)$f(x)= \begin{cases} x+1 & \text{if $x < 1$} \\ x^3 & \text{if $x {\geq} 1$} \end{cases}$

45)$f(x)= \begin{cases} |x| & \text{if $x < 2$} \\ 1 & \text{if $x {\geq} 2$} \end{cases}$

Responda

domínio:$(−\infty,\infty)$

Numérico

Para os exercícios 46-48, considerando cada função$f$$f(−3)$, avalie$f(−2)$$f(−1)$,,$f(0)$ e.

46)$f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}$

47)$f(x)= \begin{cases} 1 & \text{if $x \leq -3$} \\ 0 & \text{if $x > -3$} \end{cases}$

Responda

$f(−3)=1$;$f(−2)=0$;$f(−1)=0$;$f(0)=0$

48)$f(x)= \begin{cases} -2x^2+3 & \text{if $x \leq -1$} \\ 5x-7 & \text{if $x > -1$} \end{cases}$

Para os exercícios 49-51, considerando cada função$f$$f(−1)$, avalie$f(0)$$f(2)$,,$f(4)$ e.

49)$f(x)= \begin{cases} 7x+3 & \text{if $x < 0$} \\ 7x+6 & \text{if $x {\geq} 0$} \end{cases}$

Responda

$f(−1)=−4$;$f(0)=6$;$f(2)=20$;$f(4)=34$

50)$f(x)= \begin{cases} x^2-2 & \text{if $x < 2$} \\ 4+|x-5| & \text{if $x {\geq} 2$} \end{cases}$

51)$f(x)= \begin{cases} 5x & \text{if $x < 0$} \\ 3 & \text{if $0 {\geq} x {\leq} 2$} \\ x^2 & \text{if $x > 3$} \end{cases}$

Responda

$f(−1)=−5$;$f(0)=3$;$f(2)=3$;$f(4)=16$

Para os exercícios 52-54, escreva o domínio para a função por partes na notação de intervalo.

52)$f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}$

53)$f(x)= \begin{cases} x^2-2 & \text{if $x < 1$} \\ -x^2+2 & \text{if $x > 1$} \end{cases}$

Responda

domínio:$(−\infty,1)\cup(1,\infty)$

54)$f(x)= \begin{cases} x^2-3 & \text{if $x < 0$} \\ -3x^2 & \text{if $x {\geq} 2$} \end{cases}$

Tecnologia

55) Gráfico$y=\dfrac{1}{x^2}$ na janela de visualização$[−0.5,−0.1]$$[0.1,0.5]$ e. Determine a faixa correspondente para a janela de visualização. Mostre os gráficos.

Responda

janela:$[−0.5,−0.1]$; alcance:$[4, 100]$

janela:$[0.1, 0.5]$; alcance:$[4, 100]$

56) Gráfico$y=\dfrac{1}{x}$ na janela de visualização$[−0.5,−0.1]$$[0.1, 0.5]$ e. Determine a faixa correspondente para a janela de visualização. Mostre os gráficos.

Extensão

57) Suponha que o alcance de uma função$f$ seja$[−5, 8]$. Qual é o alcance de$|f(x)|$?

Responda

$[0, 8]$

58) Crie uma função na qual o intervalo seja todo de números reais não negativos.

59) Crie uma função na qual o domínio esteja$x>2$.

Responda

Muitas respostas. Uma função é$f(x)=\dfrac{1}{\sqrt{x-2}}$.

Aplicativos do mundo real

60) A altura$h$ de um projétil é uma função do tempo em$t$ que ele está no ar. A altura em pés por$t$ segundos é dada pela função$h(t)=−16t^2+96t$. Qual é o domínio da função? O que o domínio significa no contexto do problema?

Responda

O domínio é$[0, 6]$; leva 6 segundos para o projétil sair do chão e retornar ao chão

61) O custo em dólares da fabricação de$x$ itens é dado pela função$C(x)=10x+500$.

a. O custo fixo é determinado quando nenhum item é produzido. Encontre o custo fixo desse item.

b. Qual é o custo de fabricação de$25$ itens?

c. Suponha que o custo máximo permitido seja$\$1500$. Quais são o domínio e o alcance da função de custo$C(x)$?

1.3: Taxas de mudança e comportamento dos gráficos

Nesta seção, investigaremos as mudanças nas funções. Por exemplo, uma taxa de variação relaciona uma alteração em uma quantidade de saída a uma mudança em uma quantidade de entrada. A taxa média de mudança é determinada usando somente os dados iniciais e finais. Os pontos de identificação que marcam o intervalo em um gráfico podem ser usados para encontrar a taxa média de variação. A comparação de pares de valores de entrada e saída em uma tabela também pode ser usada para encontrar a taxa média de variação.

Verbal

1) A taxa média de variação de uma função pode ser constante?

Responda

Sim, a taxa média de variação de todas as funções lineares é constante.

2) Se uma função$f$ está aumentando$(a,b)$ e diminuindo$(b,c)$, então o que pode ser dito sobre a extremidade local de$f$ on$(a,c)$?

3) Como o máximo e o mínimo absolutos são semelhantes e diferentes dos extremos locais?

Responda

O máximo e o mínimo absolutos estão relacionados ao gráfico inteiro, enquanto os extremos locais se relacionam apenas com uma região específica em torno de um intervalo aberto.

4) Como o gráfico da função de valor absoluto se compara ao gráfico da função quadrática,$y=x^2$, em termos de intervalos crescentes e decrescentes?

Algébrico

Para os exercícios 5-15, encontre a taxa média de variação de cada função no intervalo especificado para números reais$b$ ou$h$.

5)$f(x)=4x^2−7$ em$[1, b]$

Responda

$4(b+1)$

6)$g(x)=2x^2−9$ em$[4, b]$

7)$p(x)=3x+4$ em$[2, 2+h]$

Responda

$3$

8)$k(x)=4x−2$ em$[3, 3+h]$

9)$f(x)=2x^2+1$ em$[x,x+h]$

Responda

$4x+2h$

10)$g(x)=3x^2−2$ em$[x,x+h]$

11)$a(t)=\dfrac{1}{t+4}$ em$[9,9+h]$

Responda

$\dfrac{−1}{13(13+h)}$

12)$b(x)=1x+3$ em$[1,1+h]$

13)$j(x)=3x^3$ em$[1,1+h]$

Responda

$3h^2+9h+9$

14)$r(t)=4t^3$ em$[2,2+h]$

15)$\dfrac{f(x+h)−f(x)}{h}$ dado$f(x)=2x^2−3x$ em$[x,x+h]$

Responda

$4x+2h−3$

Gráfica

Para os exercícios 16-17, considere o gráfico de$f$ mostrado na Figura abaixo

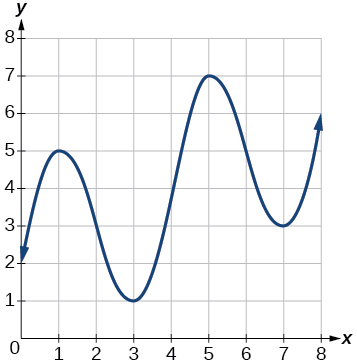
Gráfico de um polinômio.

16) Estime a taxa média de variação$x=1$ de$x=4$ a.

17) Estime a taxa média de variação$x=2$ de$x=5$ a.

Responda

$\dfrac{4}{3}$

Para os exercícios a seguir, use o gráfico de cada função para estimar os intervalos nos quais a função está aumentando ou diminuindo.

18)

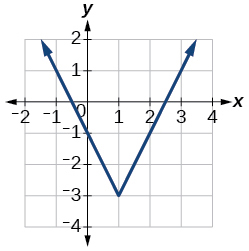
19)

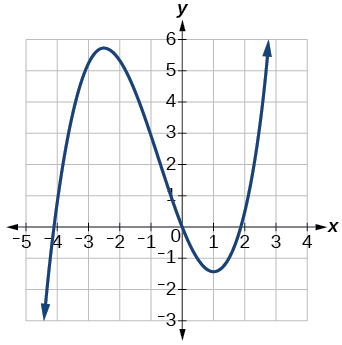
Responda

aumentando em$(−\infty,−2.5)\cup(1,\infty)$, diminuindo em$(−2.5, 1)$

20)

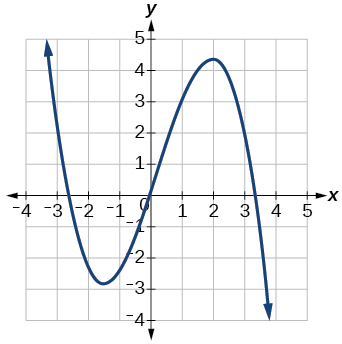
21)

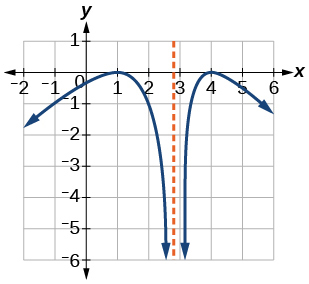
Responda

aumentando em$(−\infty,1)\cup(3,4)$, diminuindo em$(1,3)\cup(4,\infty)$

Para os exercícios 22-23, considere o gráfico mostrado na Figura abaixo.

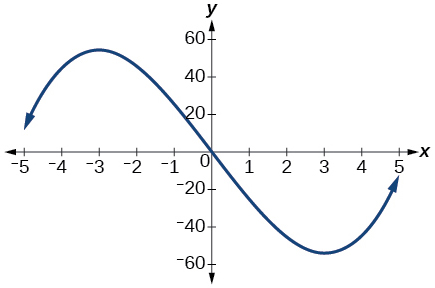
Gráfico de uma função cúbica.

22) Estime os intervalos em que a função está aumentando ou diminuindo.

23) Estime o (s) ponto (s) em que o gráfico de f tem um máximo local ou um mínimo local.

Responda

máximo local:$(−3, 60)$, mínimo local:$(3, −60)$

Para os exercícios 24-25, considere o gráfico na Figura abaixo.

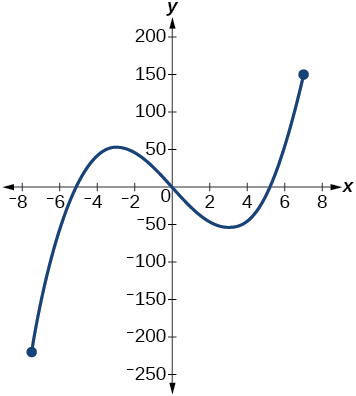
Gráfico de uma função cúbica.

24) Se o gráfico completo da função for mostrado, estime os intervalos em que a função está aumentando ou diminuindo.

25) Se o gráfico completo da função for mostrado, estime o máximo absoluto e o mínimo absoluto.

Responda

máximo absoluto em aproximadamente$(7, 150)$, mínimo absoluto em aproximadamente$(−7.5, −220)$

Numérico

26) A tabela abaixo mostra as vendas anuais (em milhões de dólares) de um produto de 1998 a 2006. Qual foi a taxa média de variação das vendas anuais (a) entre 2001 e 2002 e (b) entre 2001 e 2004?

Ano	Vendas (milhões de dólares)
1998	201
1999	219
2000	233
2001	243
2002	249
2003	251
2004	249
2005	243
2006	233

27) A tabela abaixo mostra a população de uma cidade (em milhares) de 2000 a 2008. Qual foi a taxa média de variação da população (a) entre 2002 e 2004 e (b) entre 2002 e 2006?

Ano	População (milhares)
2000	87
2001	84
2002	83
2003	80
2004	77
2005	76
2006	78
2007	81
2008	85

Responda

a.$-3000$; b.$-1250$

Para os exercícios 28-34, encontre a taxa média de variação de cada função no intervalo especificado.

28)$f(x)=x^2$ em$[1, 5]$

29)$h(x)=5−2x^2$ em$[−2,4]$

Responda

$-4$

30)$q(x)=x^3$ em$[−4,2]$

31)$g(x)=3x^3−1$ em$[−3,3]$

Responda

$27$

32)$y=\dfrac{1}{x}$ em$[1, 3]$

33)$p(t)=\dfrac{(t^2-4)(t+1)}{t^2+3}$ em$[-3,1]$

Responda

$-0.167$

34)$k(t)=6t^2+\dfrac{4}{t^3}$ em$[−1,3]$

Tecnologia

Para os exercícios 35-40, use um utilitário gráfico para estimar a extremidade local de cada função e estimar os intervalos nos quais a função está aumentando e diminuindo.

35)$f(x)=x^4−4x^3+5$

Responda

Mínimo local em$(3,−22)$, diminuindo em$(−\infty, 3)$, aumentando em$(3, \infty)$

36)$h(x)=x^5+5x^4+10x^3+10x^2−1$

37)$g(t)=t\sqrt{t+3}$

Responda

Mínimo local em$(−2,−2)$, diminuindo em$(−3,−2)$, aumentando em$(−2, \infty)$

38)$k(t)=3t^{\frac{2}{3}}−t$

39)$m(x)=x^4+2x^3−12x^2−10x+4$

Responda

Máximo local em$(−0.5, 6)$, mínimos locais em$(−3.25,−47)$ e$(2.1,−32)$, diminuindo em$(−\infty,−3.25)$ e$(−0.5, 2.1)$, aumentando em$(−3.25, −0.5)$ e$(2.1,\infty)$

40)$n(x)=x^4−8x^3+18x^2−6x+2$

Extensão

41) O gráfico da função$f$ é mostrado na Figura abaixo:

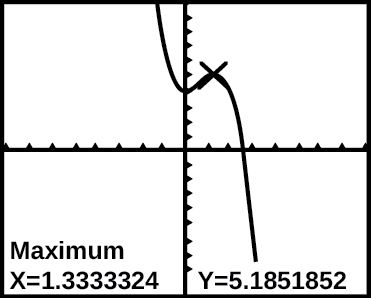
Gráfico de f (x) em uma calculadora gráfica.

Com base na captura de tela da calculadora, o ponto$(1.333, 5.185)$ é qual das seguintes opções?

1. um máximo relativo (local) da função
2. o vértice da função
3. o máximo absoluto da função
4. um zero da função

Responda

uma

42) Deixe$f(x)=\dfrac{1}{x}$. Encontre um número$c$ tal que seja a taxa média de variação da função f no intervalo$(1,c)$$-\dfrac{1}{4}$.

43) Deixe$f(x)=\dfrac{1}{x}$. Encontre o número de$b$ forma que a taxa média de variação de f no intervalo$(2,b)$ seja$−\dfrac{1}{10}$.

Responda

$b=5$

Aplicativos do mundo real

44) No início de uma viagem, o odômetro de um carro era lido$21,395$. No final da viagem,$13.5$ horas depois, o odômetro era lido$22,125$. Suponha que a escala no odômetro esteja em milhas. Qual é a velocidade média que o carro percorreu durante essa viagem?

45) Um motorista de um carro parou em um posto de gasolina para encher seu tanque de gasolina. Ele olhou para o relógio e a hora era exatamente 15h40. Nesse momento, ele começou a bombear gasolina para o tanque. Exatamente às 3:44, o tanque estava cheio e ele percebeu que havia bombeado$10.7$ galões. Qual é a taxa média de fluxo da gasolina no tanque de gasolina?

Responda

$2.7$galões por minuto

46) Perto da superfície da lua, a distância que um objeto cai é função do tempo. É dado por$d(t)=2.6667t^2$, onde$t$ está em segundos e$d(t)$ está em pés. Se um objeto cair de uma certa altura, determine a velocidade média do objeto de$t=1$ para$t=2$.

47) O gráfico na Figura abaixo ilustra a decomposição de uma substância radioativa ao longo de$t$ dias.

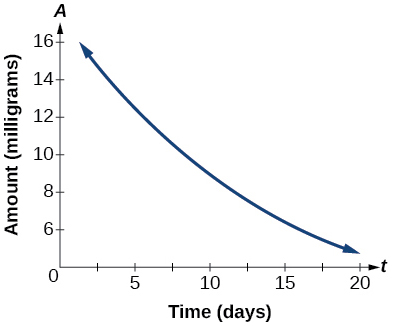
Gráfico de uma função exponencial.

Use o gráfico para estimar a taxa média de decaimento de$t=5$ para$t=15$.

Responda

aproximadamente$-0.6$ miligramas por dia

1.4: Composição das funções

Suponha que desejemos calcular quanto custa aquecer uma casa em um determinado dia do ano. O custo do aquecimento de uma casa dependerá da temperatura média diária e, por sua vez, a temperatura média diária depende do dia específico do ano. O custo depende da temperatura e a temperatura depende do dia. Ao combinar esses dois relacionamentos em uma função, realizamos a composição da função, que é o foco desta seção.

Verbal

1) Como encontrar o domínio do quociente de duas funções,$\dfrac{f}{g}$?

Responda

Encontre os números que tornam a função no denominador$g$ igual a zero e verifique se há outras restrições de domínio em$f$ e$g$, como uma raiz indexada par ou zeros no denominador.

2) Qual é a composição de duas funções$f{\circ}g$?

3) Se a ordem for invertida ao compor duas funções, o resultado pode ser o mesmo que a resposta na ordem original da composição? Se sim, dê um exemplo. Se não, explique por que não.

Responda

Sim. Exemplo de resposta: Let$f(x)=x+1$$g(x)=x−1$ e. Em seguida$f(g(x))=f(x−1)=(x−1)+1=x$,$g(f(x))=g(x+1)=(x+1)−1=x$ e. Então$f{\circ}g=g{\circ}f$.

4) Como você encontra o domínio para a composição de duas funções$f{\circ}g$?

Algébrico

5) Dado$f(x)=x^2+2x$ e$g(x)=6−x^2$, find$f+g$,$f−g$,$fg$, e$\dfrac{f}{g}$ .Determine o domínio para cada função na notação de intervalo.

Responda

$(f+g)(x)=2x+6$, domínio:$(−\infty,\infty)$

$(f−g)(x)=2x^2+2x−6$, domínio:$(−\infty,\infty)$

$(fg)(x)=−x^4−2x^3+6x^2+12x$, domínio:$(−\infty,\infty)$

$\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2+2x}{6−x^2},$domínio:$(−\infty,−\sqrt{6})\cup(\sqrt{6},\sqrt{6})\cup(\sqrt{6},\infty)$

6) Dado$f(x)=−3x^2+x$ e$g(x)=5$$f+g$, encontre$f−g$$fg$,,$\dfrac{f}{g}$ e. Determine o domínio para cada função na notação de intervalo.

7) Dado$f(x)=2x^2+4x$ e$g(x)=\dfrac{1}{2x}$$f+g$, encontre$f−g$$fg$,,$\dfrac{f}{g}$ e. Determine o domínio para cada função na notação de intervalo.

Responda

$(f+g)(x)=\dfrac{4x^3+8x^2+1}{2x}$, domínio:$(−\infty,0)\cup(0,\infty)$

$(f−g)(x)=\dfrac{4x3+8x2−1}{2x}$, domínio:$(−\infty,0)\cup(0,\infty)$

$(fg)(x)=x+2$, domínio:$(−\infty,0)\cup(0,\infty)$

$(fg)(x)=4x^3+8x^2$, domínio:$(−\infty,0)\cup(0,\infty)$

8) Dado$f(x)=\dfrac{1}{x−4}$ e$g(x)=\dfrac{1}{6−x}$$f+g$, encontre$f−g$$fg$,,$\dfrac{f}{g}$ e. Determine o domínio para cada função na notação de intervalo.

9) Dado$f(x)=3x^2$ e$g(x)=\sqrt{x−5}$$f+g$, encontre$f−g$$fg$,,$\dfrac{f}{g}$ e. Determine o domínio para cada função na notação de intervalo.

Responda

$(f+g)(x)=3x^2+\sqrt{x−5}$, domínio:$\left[5,\infty\right)$

$(f−g)(x)=3x^2−\sqrt{x−5}$, domínio:$\left[5,\infty\right)$

$(fg)(x)=3x^2\sqrt{x−5}$, domínio:$\left[5,\infty\right)$

$\left(\dfrac{f}{g}\right)(x)=\dfrac{3x^2}{\sqrt{x−5}}$, domínio:$(5,\infty)$

10) Dado$f(x)=\sqrt{x}$ e$g(x)=|x−3|$, encontre$\dfrac{g}{f}$. Determine o domínio da função na notação de intervalo.

11) Dado$f(x)=2x^2+1$ e$g(x)=3x−5$, encontre o seguinte:

1. $f(g(2))$
2. $f(g(x))$
3. $g(f(x))$
4. $(g{\circ}g)(x)$
5. $(f{\circ}f)(−2)$

Responda

1. $3$
2. $f(g(x))=2(3x−5)^2+1$
3. $f(g(x))=6x^2−2$
4. $(g{\circ}g)(x)=3(3x−5)−5=9x−20$
5. $(f{\circ}f)(−2)=163$

Para os exercícios 12-17, use cada par de funções para encontrar$f(g(x))$$g(f(x))$ e. Simplifique suas respostas.

12)$f(x)=x^2+1$,$g(x)=\sqrt{x+2}$

13)$f(x)=\sqrt{x}+2$,$g(x)=x^2+3$

Responda

$f(g(x))=\sqrt{x+3}$,$g(f(x))=x+4\sqrt{x}+7$

14)$f(x)=|x|$,$g(x)=5x+1$

15)$f(x)=\sqrt[3]{x}$,$g(x)=\dfrac{x+1}{x^3}$

Responda

$f(g(x))=\sqrt[3]{\dfrac{x+1}{x^3}}=\dfrac{\sqrt[3]{x+1}}{x}$,$g(f(x))=\dfrac{\sqrt[3]{x}+1}{x}$

16)$f(x)=\dfrac{1}{x−6}$,$g(x)=\dfrac{7}{x}+6$

17)$f(x)=\dfrac{1}{x−4}$,$g(x)=\dfrac{2}{x}+4$

Responda

$(f{\circ}g)(x)=\dfrac{1}{\frac{2}{x}+4-4}=\dfrac{x}{2}$,$(g{\circ}f)(x)=2x-4$

Para os exercícios 18-25, use cada conjunto de funções para encontrar f (g (h (x))). Simplifique suas respostas.

18)$f(x)=x^4+6$$g(x)=x−6$, e$h(x)=\sqrt{x}$

19)$f(x)=x^2+1$,$g(x)=\dfrac{1}{x}$, e$h(x)=x+3$

Responda

$f(g(h(x)))=\left(\dfrac{1}{x+3}\right)^2+1$

20) Dado$f(x)=\dfrac{1}{x}$ e$g(x)=x−3$, encontre o seguinte:

1. $(f{\circ}g)(x)$
2. o domínio de$(f{\circ}g)(x)$ em notação de intervalo
3. $(g{\circ}f)(x)$
4. o domínio de$(g{\circ}f)(x)$
5. $\left(\dfrac{f}{g}\right)x$

21) Dado$f(x)=\sqrt{2−4x}$ e$g(x)=−\dfrac{3}{x}$, encontre o seguinte:

1. $(g{\circ}f)(x)$
2. o domínio de$(g{\circ}f)(x)$ em notação de intervalo

Responda

1. $(g{\circ}f)(x)=−\dfrac{3}{\sqrt{2−4x}}$
2. $\left(−\infty,\dfrac{1}{2}\right)$

22) Dadas as funções$f(x)=\dfrac{1−x}{x}$ e$g(x)=\dfrac{1}{1+x^2}$, encontre o seguinte:

1. $(g{\circ}f)(x)$
2. $(g{\circ}f)(2)$

23) Dadas as funções$p(x)=\dfrac{1}{\sqrt{x}}$ e$m(x)=x^2−4$, declare o domínio de cada uma das seguintes funções usando a notação de intervalo:

1. $\dfrac{p(x)}{m(x)}$
2. $p(m(x))$
3. $m(p(x))$

Responda

1. $(0,2)\cup(2,\infty)$
2. $(−\infty,−2)\cup(2,\infty)$
3. $(0,\infty)$

24) Dadas funções$q(x)=\dfrac{1}{\sqrt{x}}$ e$h(x)=x^2−9$, indique o domínio de cada uma das seguintes funções usando a notação de intervalo.

1. $\dfrac{q(x)}{h(x)}$
2. $q(h(x))$
3. $h(q(x))$

25) Para$f(x)=\dfrac{1}{x}$ e$g(x)=\sqrt{x−1}$, escreva o domínio de$(f{\circ}g)(x)$ em notação de intervalo.

Responda

$(1,\infty)$

Para os exercícios 26-41, encontre funções$f(x)$ e,$g(x)$ portanto, a função dada pode ser expressa como$h(x)=f(g(x))$.

26)$h(x)=(x+2)^2$

27)$h(x)=(x−5)^3$

Responda

amostra:$f(x)=x^3$

$g(x)=x−5$

28)$h(x)=\dfrac{3}{x−5}$

29)$h(x)=\dfrac{4}{(x+2)^2}$

Responda

amostra:$f(x)=\dfrac{4}{x}$

$g(x)=(x+2)^2$

30)$h(x)=4+\sqrt[3]{x}$

31)$h(x)=\sqrt[3]{\dfrac{1}{2x−3}}$

Responda

amostra:$f(x)=\sqrt[3]{x}$

$g(x)=\dfrac{1}{2x−3}$

32)$h(x)=\dfrac{1}{(3x^2−4)^{−3}}$

33)$h(x)=\sqrt[4]{\dfrac{3x−2}{x+5}}$

Responda

amostra:$f(x)=\sqrt[4]{x}$

$g(x)=\dfrac{3x−2}{x+5}$

34)$h(x)=(\dfrac{8+x^3}{8−x^3})^4$

35)$h(x)=\sqrt{2x+6}$

Responda

amostra:$f(x)=\sqrt{x}$

$g(x)=2x+6$

36)$h(x)=(5x−1)^3$

37)$h(x)=\sqrt[3]{x−1}$

Responda

amostra:$f(x)=\sqrt[3]{x}$
$g(x)=(x−1)$

38)$h(x)=|x^2+7|$

39)$h(x)=\dfrac{1}{(x−2)^3}$

Responda

amostra:$f(x)=x^3$
$g(x)=\dfrac{1}{x−2}$

40)$h(x)=\left(\dfrac{1}{2x−3}\right)^2$

41)$h(x)=\sqrt { \dfrac{2x−1}{3x+4}}$

Responda

amostra:$f(x)=\sqrt{x}$
$g(x)=\dfrac{2x−1}{3x+4}$

Gráfica

Para os exercícios 42-49, use os gráficos de$f$, mostrados na Figura 1 e$g$, mostrados na Figura 2, para avaliar as expressões.

Figura 1: Gráfico de uma função.

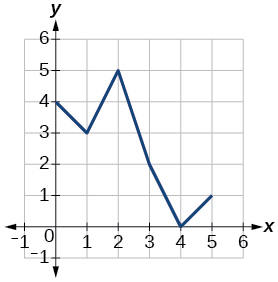
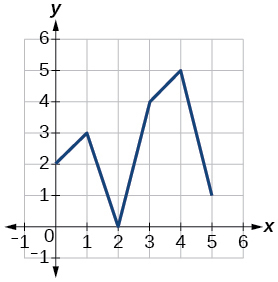
Figura 2: Gráfico de uma função.

42)$f(g(3))$

43)$f(g(1))$

Responda

$2$

44)$g(f(1))$

45)$g(f(0))$

Responda

$5$

46)$f(f(5))$

47)$f(f(4))$

Responda

$4$

48)$g(g(2))$

49)$g(g(0))$

Responda

$0$

Para os exercícios 50-57, use gráficos de$f(x)$, mostrados na Figura 3$g(x)$, mostrados na Figura 4 e$h(x)$, mostrados na Figura 5, para avaliar as expressões.

Figura 3: Gráfico de uma parábola.

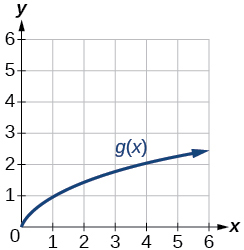
Figura 4: Gráfico de uma função de raiz quadrada.

Figura 5: Gráfico de uma função de valor absoluto.

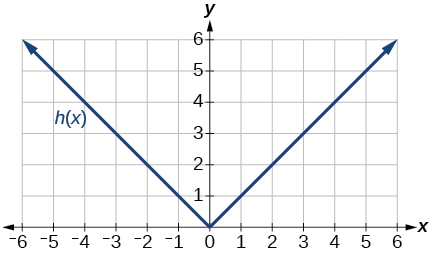
50)$g(f(1))$

51)$g(f(2))$

Responda

$2$

52)$f(g(4))$

53)$f(g(1))$

Responda

$1$

54)$f(h(2))$

55)$h(f(2))$

Responda

$4$

56)$f(g(h(4)))$

57)$f(g(f(−2)))$

Responda

$4$

Numérico

Para os exercícios 58-65, use os valores da função para$f$ e$g$ mostrados na Tabela abaixo para avaliar cada expressão.

$x$	$f(x)$	$g(x)$
\ (x\) ">0	\ (f (x)\) ">7	\ (g (x)\) ">9
\ (x\) ">1	\ (f (x)\) ">6	\ (g (x)\) ">5
\ (x\) ">2	\ (f (x)\) ">5	\ (g (x)\) ">6
\ (x\) ">3	\ (f (x)\) ">8	\ (g (x)\) ">2
\ (x\) ">4	\ (f (x)\) ">4	\ (g (x)\) ">1
\ (x\) ">5	\ (f (x)\) ">0	\ (g (x)\) ">8
\ (x\) ">6	\ (f (x)\) ">2	\ (g (x)\) ">7
\ (x\) ">7	\ (f (x)\) ">1	\ (g (x)\) ">3
\ (x\) ">8	\ (f (x)\) ">9	\ (g (x)\) ">4
\ (x\) ">9	\ (f (x)\) ">3	\ (g (x)\) ">0

(58)$f(g(8))$

59)$f(g(5))$

Responda

$9$

60)$g(f(5))$

61)$g(f(3))$

Responda

$4$

62)$f(f(4))$

63)$f(f(1))$

Responda

$2$

64)$g(g(2))$

65)$g(g(6))$

Responda

$3$

Para os exercícios 66-71, use os valores da função para$f$ e$g$ mostrados na tabela abaixo para avaliar as expressões.

$x$	$f(x)$	$g(x)$
\ (x\) ">-3	\ (f (x)\) ">11	\ (g (x)\) ">-8
\ (x\) ">-2	\ (f (x)\) ">9	\ (g (x)\) ">-3
\ (x\) ">-1	\ (f (x)\) ">7	\ (g (x)\) ">0
\ (x\) ">0	\ (f (x)\) ">5	\ (g (x)\) ">1
\ (x\) ">1	\ (f (x)\) ">3	\ (g (x)\) ">0
\ (x\) ">2	\ (f (x)\) ">1	\ (g (x)\) ">-3
\ (x\) ">3	\ (f (x)\) ">-1	\ (g (x)\) ">-8

66)$(f{\circ}g)(1)$

67)$(f{\circ}g)(2)$

Responda

$11$

68)$(g{\circ}f)(2)$

69)$(g{\circ}f)(3)$

Responda

$0$

70)$(g{\circ}g)(1)$

71)$(f{\circ}f)(3)$

Responda

$7$

Para os exercícios 72-75, use cada par de funções para encontrar$f(g(0))$$g(f(0))$ e.

72)$f(x)=4x+8$,$g(x)=7−x^2$

73)$f(x)=5x+7$,$g(x)=4−2x^2$

Responda

$f(g(0))=27$,$g(f(0))=−94$

74)$f(x)=\sqrt{x+4}$,$g(x)=12−x^3$

75)$f(x)=\frac{1}{x+2}$,$g(x)=4x+3$

Responda

$f(g(0))=\frac{1}{5}$,$g(f(0))=5$

Para os exercícios 76-79, use as funções$f(x)=2x^2+1$ e$g(x)=3x+5$ para avaliar ou encontrar a função composta conforme indicado.

76)$f(g(2))$

77)$f(g(x))$

Responda

$18x^2+60x+51$

78)$g(f(−3))$

79)$(g{\circ}g)(x)$

Responda

$g{\circ}g(x)=9x+20$

Extensões

Para os exercícios 80-84, use$f(x)=x^3+1$$g(x)=\sqrt[3]{x−1}$ e.

80) Encontre$(f{\circ}g)(x)$$(g{\circ}f)(x)$ e. Compare as duas respostas.

81) Encontre$(f{\circ}g)(2)$$(g{\circ}f)(2)$ e.

Responda

$2$

82) Qual é o domínio de$(g{\circ}f)(x)$?

83) Qual é o domínio de$(f{\circ}g)(x)$?

Responda

$(−\infty,\infty)$

84) Deixe$f(x)=\frac{1}{x}$.

1. Encontre$(f{\circ}f)(x)$.
2. $(f{\circ}f)(x)$Para qualquer função é$f$ o mesmo resultado da resposta à parte (a) de qualquer função? Explique.

Para os exercícios 85-87$F(x)=(x+1)^5$, deixe$f(x)=x^5$,$g(x)=x+1$ e.

85) Verdadeiro ou falso:$(g{\circ}f)(x)=F(x)$.

Responda

Falso

86) Verdadeiro ou falso:$(f{\circ}g)(x)=F(x)$.

Para os exercícios 87-89, encontre a composição quando$f(x)=x^2+2$ para todos$x\geq0$$g(x)=\sqrt{x−2}$ e.

87)$(f{\circ}g)(6)$;$(g{\circ}f)(6)$

Responda

$(f{\circ}g)(6)=6$;$(g{\circ}f)(6)=6$

88)$(g{\circ}f)(a)$;$(f{\circ}g)(a)$

89)$(f{\circ}g)(11)$;$(g{\circ}f)(11)$

Responda

$(f{\circ}g)(11)=11$,$(g{\circ}f)(11)=11$

Aplicativos do mundo real

90) A função$D(p)$ fornece o número de itens que serão exigidos quando o preço for$p$. O custo de produção$C(x)$ é o custo de produção dos$x$ itens. Para determinar o custo de produção quando o preço é$\$6$, você faria qual das seguintes opções?

1. Avalie$D(C(6))$
2. Avalie$C(D(6))$
3. Resolver$D(C(x))=6$
4. Resolver$C(D(p))=6$

91) A função$A(d)$ fornece o nível de dor em uma escala de$0$ até o$10$ experimentado por uma paciente com$d$ miligramas de um medicamento para reduzir a dor em seu sistema. Os miligramas do medicamento no sistema do paciente após$t$ minutos são modelados por$m(t)$. Qual das opções a seguir você faria para determinar quando o paciente estará com um nível de dor de$4$?

1. Avalie$A(m(4))$
2. Avalie$m(A(4))$
3. Resolver$A(m(t))=4$
4. Resolver$m(A(d))=4$

Responda

c

92) Uma loja oferece aos clientes um$30\%$ desconto no preço$x$ dos itens selecionados. Em seguida, a loja retira um adicional$15\%$ na caixa registradora. Escreva uma função de preço$P(x)$ que calcule o preço final do item em termos do preço original$x$. (Dica: use a composição da função para encontrar sua resposta.)

93) Uma gota de chuva atingindo um lago produz uma ondulação circular. Se o raio, em polegadas, crescer em função do tempo em minutos$r(t)=25\sqrt{t+2}$, de acordo com, encontre a área da ondulação em função do tempo. Encontre a área da ondulação em$t=2$.

Responda

$A(t)=\pi(25\sqrt{t+2})^2$e polegadas$A(2)=\pi(25\sqrt{4})^2=2500\pi$ quadradas

94) Um incêndio florestal deixa para trás uma área de grama queimada em um padrão circular em expansão. Se o raio do círculo de grama queimada estiver aumentando com o tempo de acordo com a fórmula$r(t)=2t+1$, expresse a área queimada em função do tempo,$t$ (minutos).

95) Use a função que você encontrou no exercício anterior para encontrar a área total queimada após$5$ minutos.

Responda

$A(5)=\pi(2(5)+1)2=121\pi$unidades quadradas

96) O raio$r$, em polegadas, de um balão esférico está relacionado ao volume,$V$, por$r(V)=\sqrt[3]{\frac{3V}{4\pi}}$. O ar é bombeado para o balão, então o volume após$t$ segundos é dado por$V(t)=10+20t$.

1. Encontre a função composta$r(V(t))$.
2. Encontre a hora exata em que o raio atinge 10 polegadas.

97) O número de bactérias em um produto alimentício refrigerado é dado por$N(T)=23T^2−56T+1$$3<T<33$,, onde$T$ está a temperatura do alimento. Quando o alimento é retirado da geladeira, a temperatura é dada por$T(t)=5t+1.5$, onde$t$ está o tempo em horas.

1. Encontre a função composta$N(T(t))$.
2. Encontre a hora (arredondada para duas casas decimais) em que a contagem de bactérias chega a 6752.

Responda

1. $N(T(t))=23(5t+1.5)^2−56(5t+1.5)+1$
2. $3.38$horas

1.5: Transformação de funções

Muitas vezes, quando temos um problema, tentamos modelar o cenário usando matemática na forma de palavras, tabelas, gráficos e equações. Um método que podemos empregar é adaptar os gráficos básicos das funções do kit de ferramentas para criar novos modelos para um determinado cenário. Existem formas sistemáticas de alterar funções para construir modelos apropriados para os problemas que estamos tentando resolver.

Verbal

1) Ao examinar a fórmula de uma função que é o resultado de várias transformações, como você pode diferenciar uma mudança horizontal de uma mudança vertical?

Responda

Um deslocamento horizontal ocorre quando uma constante é adicionada ou subtraída da entrada. Uma mudança vertical ocorre quando uma constante é adicionada ou subtraída da saída.

2) Ao examinar a fórmula de uma função que é o resultado de várias transformações, como diferenciar um alongamento horizontal de um trecho vertical?

3) Ao examinar a fórmula de uma função que é o resultado de várias transformações, como diferenciar uma compressão horizontal de uma compressão vertical?

Responda

Uma compressão horizontal ocorre quando uma constante maior que$1$ é multiplicada pela entrada. Uma compressão vertical ocorre quando uma constante entre$0$ e$1$ é multiplicada pela saída.

4) Ao examinar a fórmula de uma função que é o resultado de múltiplas transformações, como você pode diferenciar uma reflexão em relação ao$x$ eixo -de uma reflexão em relação ao$y$ eixo -?

5) Como você pode determinar se uma função é ímpar ou par a partir da fórmula da função?

Responda

Para uma função$f$, substitua (−x) por (x) em$f(x)$. Simplifique. Se a função resultante for igual à função original$f(−x)=f(x)$, a função será uniforme. Se a função resultante for o oposto da função original$f(−x)=−f(x)$, a função original será ímpar. Se a função não for a mesma ou o contrário, a função não é ímpar nem par.

Algébrico

6) Escreva uma fórmula para a função obtida quando o gráfico de$f(x)=\sqrt{x}$ é deslocado para cima da$1$ unidade e para as$2$ unidades da esquerda.

7) Escreva uma fórmula para a função obtida quando o gráfico de$f(x)=|x|$ é deslocado para baixo em$3$ unidades e para a$1$ unidade direita.

Responda

$g(x)=|x-1|−3$

8) Escreva uma fórmula para a função obtida quando o gráfico de$f(x)=\dfrac{1}{x}$ é deslocado para baixo em$4$ unidades e para as$3$ unidades corretas.

9) Escreva uma fórmula para a função obtida quando o gráfico de$f(x)=\dfrac{1}{x^2}$ é deslocado para cima em$2$ unidades e para as$4$ unidades esquerdas.

Responda

$g(x)=\dfrac{1}{(x+4)^2}+2$

Para os exercícios 10-19, descreva como o gráfico da função é uma transformação do gráfico da função original$f$.

10)$y=f(x−49)$

11)$y=f(x+43)$

Responda

O gráfico de$f(x+43)$ é um deslocamento horizontal para as$43$ unidades esquerdas do gráfico de$f$.

12)$y=f(x+3)$

13)$y=f(x−4)$

Responda

O gráfico de$f(x-4)$ é um deslocamento horizontal para as$4$ unidades direitas do gráfico de$f$.

14)$y=f(x)+5$

15)$y=f(x)+8$

Responda

O gráfico de$f(x)+8$ é um deslocamento vertical para cima das$8$ unidades do gráfico de$f$.

16)$y=f(x)−2$

17)$y=f(x)−7$

Responda

O gráfico de$f(x)−7$ é um deslocamento vertical para baixo das$7$ unidades do gráfico de$f$.

18)$y=f(x−2)+3$

19)$y=f(x+4)−1$

Responda

O gráfico de$f(x+4)−1$ é um deslocamento horizontal para as$4$ unidades da esquerda e uma$1$ unidade vertical para baixo do gráfico de$f$.

Para os exercícios 20-23, determine o (s) intervalo (s) em que a função está aumentando e diminuindo.

20)$f(x)=4(x+1)^2−5$

21)$g(x)=5(x+3)^2−2$

Responda

diminuindo$(−\infty,−3)$ e aumentando$(−3,\infty)$

22)$a(x)=\sqrt{−x+4}$

23)$k(x)=−3\sqrt{x}−1$

Responda

diminuindo em$(0, \infty)$

Gráfica

Para os exercícios 24-26, use o gráfico$f(x)=2^x$ mostrado na Figura abaixo para esboçar um gráfico de cada transformação de$f(x)$.

\ (f (x)\).” style="largura: 301px; altura: 306px;” width="301px” altura="306px” src=” https://math.libretexts.org/@api/dek..._01_05_201.jpg "/>

Gráfico de$f(x)$.

25)$h(x)=2^x−3$

24)$g(x)=2^x+1$

Responda

\ (k (x)\)” src=” https://math.libretexts.org/@api/dek..._01_05_202.jpg "/>

Gráfico de$k(x)$

26)$w(x)=2^x−1$

Para os exercícios 27-30, esboce um gráfico da função como uma transformação do gráfico de uma das funções do kit de ferramentas.

27)$f(t)=(t+1)^2−3$

Responda

\ (f (t)\).” src=” https://math.libretexts.org/@api/dek..._01_05_206.jpg "/>

Gráfico de$f(t)$.

28)$h(x)=|x−1|+4$

29)$k(x)=(x−2)^3−1$

Responda

\ (k (x)\).” src=” https://math.libretexts.org/@api/dek..._01_05_208.jpg "/>

Gráfico de$k(x)$.

30)$m(t)=3+\sqrt{t+2}$

Numérico

31) As representações tabulares das funções$f$,$g$, e$h$ são fornecidas abaixo. Escreva$g(x)$ e$h(x)$ como transformações de$f(x)$.

$x$	-2	-1	0	1	2
$f(x)$	-2	-1	-3	1	2

$x$	-1	0	1	2	3
$g(x)$	-2	-1	-3	1	2

$x$	-2	-1	0	1	2
$h(x)$	-1	0	-2	2	3

Responda

$g(x)=f(x-1)$,$h(x)=f(x)+1$

32) As representações tabulares das funções$f$,$g$, e$h$ são fornecidas abaixo. Escreva$g(x)$ e$h(x)$ como transformações de$f(x)$.

$x$	-2	-1	0	1	2
$f(x)$	-1	-3	4	2	1

$x$	-3	-2	-1	0	1
$g(x)$	-1	-3	4	2	1

$x$	-2	-1	0	1	2
$h(x)$	-2	-4	3	1	0

Para os exercícios 33-40, escreva uma equação para cada função gráfica usando as transformações dos gráficos de uma das funções do kit de ferramentas.

33)

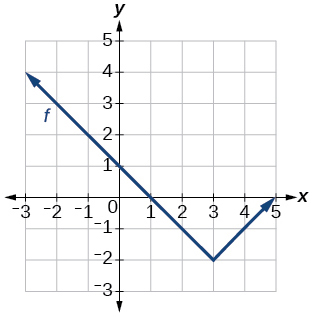
Gráfico de uma função absoluta.

Responda

$f(x)=|x-3|−2$

34)

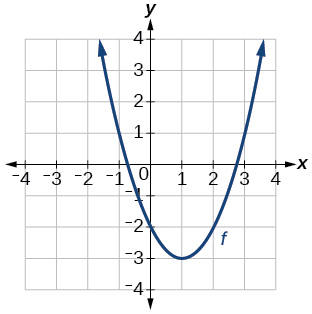
Gráfico de uma parábola.

(35)

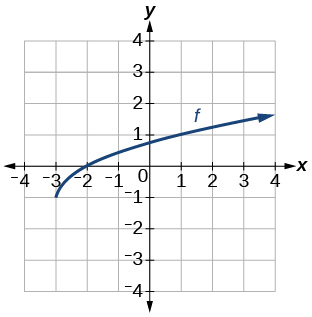
Gráfico de uma função de raiz quadrada.

Responda

$f(x)=\sqrt{x+3}−1$

36)

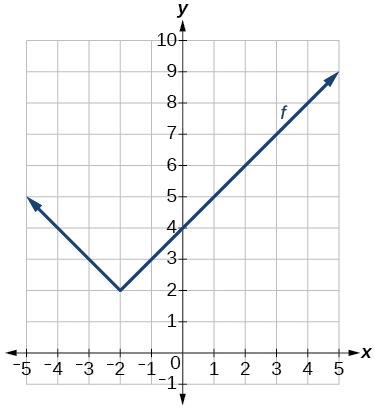
Gráfico de uma função absoluta.

37)

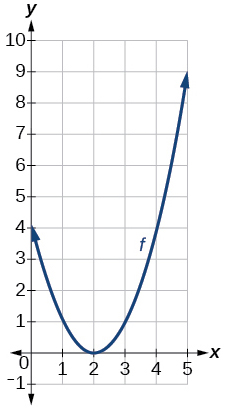
Gráfico de uma parábola

Responda

$f(x)=(x-2)^2$

38)

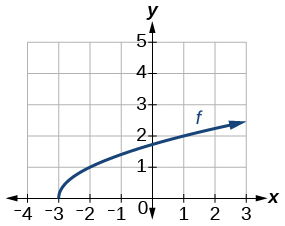
Gráfico de uma função de raiz quadrada.

39)

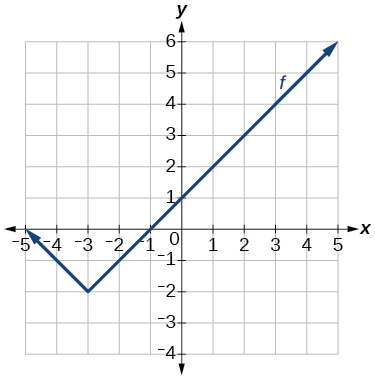
Gráfico de uma função absoluta.

Responda

$f(x)=|x+3|−2$

40)

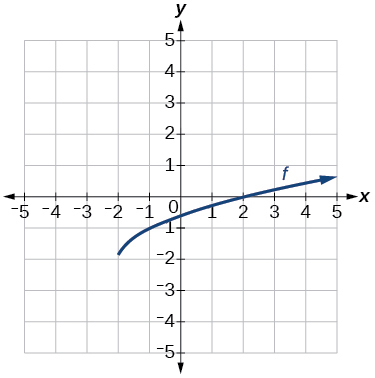
Gráfico de uma função de raiz quadrada.

Para os exercícios 41-42, use os gráficos de transformações da função de raiz quadrada para encontrar uma fórmula para cada uma das funções.

41)

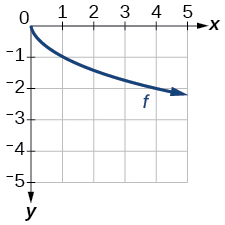
Gráfico de uma função de raiz quadrada.

Responda

$f(x)=−\sqrt{x}$

(42)

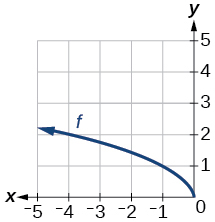
Gráfico de uma função de raiz quadrada.

Para os exercícios 43-46, use os gráficos das funções transformadas do kit de ferramentas para escrever uma fórmula para cada uma das funções resultantes.

43)

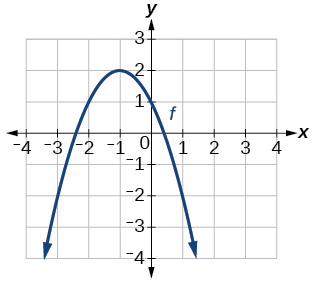
Gráfico de uma parábola.

Responda

$f(x)=−(x+1)^2+2$

44)

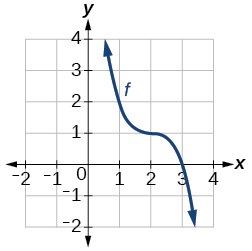
Gráfico de uma função cúbica.

45)

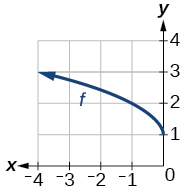
Gráfico de uma função de raiz quadrada.

Responda

$f(x)=\sqrt{−x}+1$

(46)

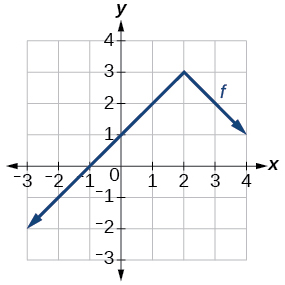
Gráfico de uma função absoluta.

Para os exercícios 47-52, determine se a função é ímpar, par ou nenhuma.

47)$f(x)=3x^4$

Responda

uniforme

48)$g(x)=\sqrt{x}$

49)$h(x)=\dfrac{1}{x}+3x$

Responda

estranha

50)$f(x)=(x−2)^2$

51)$g(x)=2x^4$

Responda

uniforme

52)$h(x)=2x−x^3$

Para os exercícios 53-62, descreva como o gráfico de cada função é uma transformação do gráfico da função original$f$.

53)$g(x)=−f(x)$

Responda

O gráfico de$g$ é uma reflexão vertical (através do eixo x) do gráfico de$f$.

54)$g(x)=f(−x)$

55)$g(x)=4f(x)$

Responda

O gráfico de$g$ é um alongamento vertical por um fator de 4 do gráfico de$f$.

(56)$g(x)=6f(x)$

57)$g(x)=f(5x)$

Responda

O gráfico de$g$ é uma compressão horizontal por um fator$15$ de do gráfico de$f$.

(58)$g(x)=f(2x)$

(59)$g(x)=f \left(\dfrac{1}{3}x \right)$

Responda

O gráfico de$g$ é um alongamento horizontal por um fator de 3 do gráfico de$f$.

60)$g(x)=f \left(\dfrac{1}{5}x \right)$

61)$g(x)=3f(−x)$

Responda

O gráfico de$g$ é uma reflexão horizontal sobre o eixo y e um alongamento vertical por um fator de 3 do gráfico de$f$.

62)$g(x)=−f(3x)$

Para os exercícios 63-68, escreva uma fórmula para a função$g$ que resulta quando o gráfico de uma determinada função do kit de ferramentas é transformado conforme descrito.

63) O gráfico de$f(x)=|x|$ é refletido sobre o$y$ eixo -e comprimido horizontalmente por um fator de$\dfrac{1}{4}$.

Responda

$g(x)=|−4x|$

64) O gráfico de$f(x)=\sqrt{x}$ é refletido sobre o$x$ eixo -e esticado horizontalmente por um fator de$2$.

65) O gráfico de$f(x)=\dfrac{1}{x^2}$ é comprimido verticalmente por um fator de e$\dfrac{1}{3}$, em seguida, deslocado para as$2$ unidades da esquerda e para baixo$3$.

Responda

$g(x)=\dfrac{1}{3(x+2)^2}−3$

66) O gráfico de$f(x)=\dfrac{1}{x}$ é esticado verticalmente por um fator de e$8$, em seguida, deslocado para as$4$ unidades certas e para cima$2$.

67) O gráfico de$f(x)=x^2$ é comprimido verticalmente por um fator de e$\dfrac{1}{2}$, em seguida, deslocado para as$5$ unidades certas e para cima$1$.

Responda

$g(x)=\dfrac{1}{2}(x-5)^2+1$

68) O gráfico de$f(x)=x^2$ é esticado horizontalmente por um fator de e$3$, em seguida, deslocado para as$4$ unidades da esquerda e para baixo$3$.

Para os exercícios 69-77, descreva como a fórmula é uma transformação de uma função do kit de ferramentas. Em seguida, esboce um gráfico da transformação.

69)$g(x)=4(x+1)^2−5$

Responda

O gráfico da função$f(x)=x^2$ é deslocado para a$1$ unidade esquerda, esticado verticalmente por um fator de$4$ e deslocado para baixo$5$ unidades.

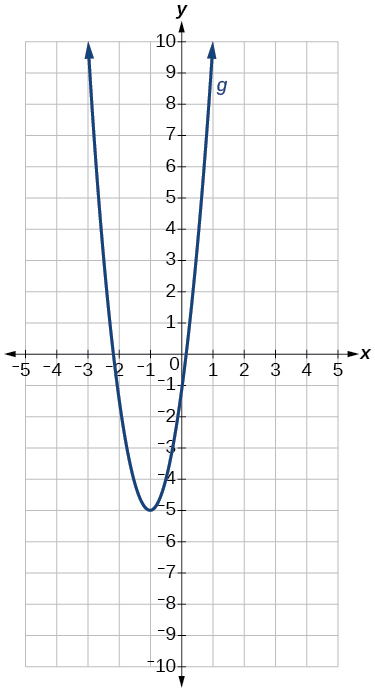
Gráfico de uma parábola.

70)$g(x)=5(x+3)^2−2$

71)$h(x)=−2|x−4|+3$

Responda

O gráfico de$f(x)=|x|$ é esticado verticalmente por um fator de$2$, deslocado horizontalmente$4$ unidades para a direita, refletido no eixo horizontal e, em seguida, deslocado verticalmente$3$ unidades para cima.

Gráfico de uma função de valor absoluto.

72)$k(x)=−3\sqrt{x}−1$

73)$m(x)=\dfrac{1}{2}x^3$

Responda

O gráfico da função$f(x)=x^3$ é comprimido verticalmente por um fator de$\dfrac{1}{2}$.

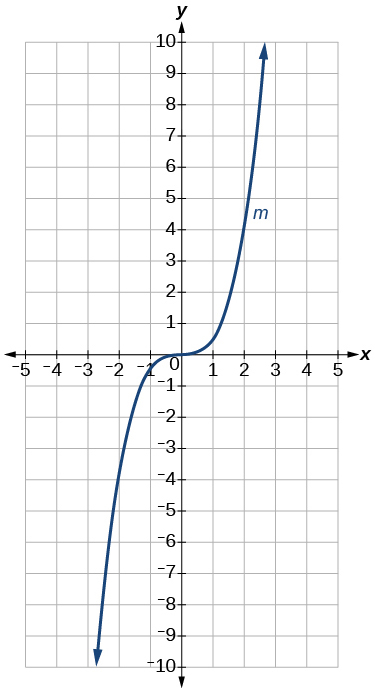
Gráfico de uma função cúbica.

74)$n(x)=\dfrac{1}{3}|x−2|$

75)$p(x)=(\dfrac{1}{3}x)^3−3$

Responda

O gráfico da função é esticado horizontalmente por um fator de$3$ e, em seguida, deslocado verticalmente para baixo em$3$ unidades.

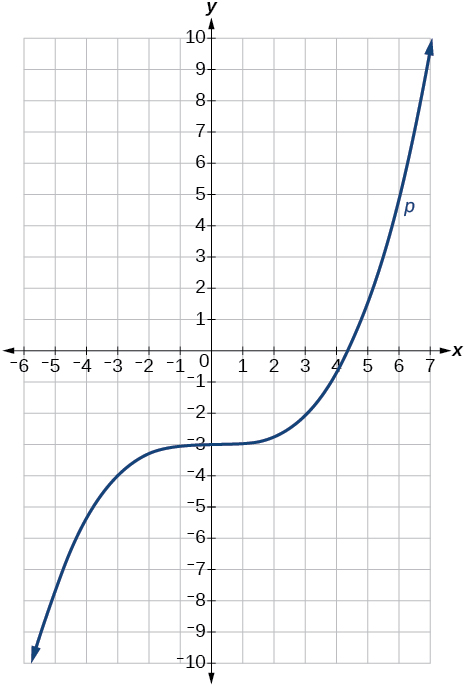
Gráfico de uma função cúbica.

76)$q(x)=(\dfrac{1}{4}x)^3+1$

77)$a(x)=\sqrt{−x+4}$

Responda

O gráfico de$f(x)=\sqrt{x}$ é deslocado em$4$ unidades para a direita e, em seguida, refletido na linha vertical$x=4$.

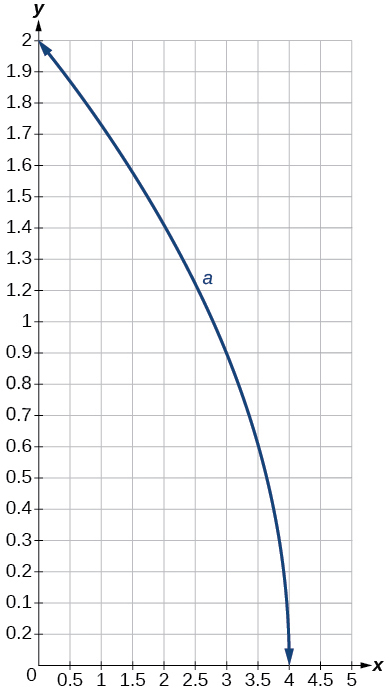
Gráfico de uma função de raiz quadrada.

Para os exercícios 78-81, use o gráfico na Figura abaixo para esboçar as transformações dadas.

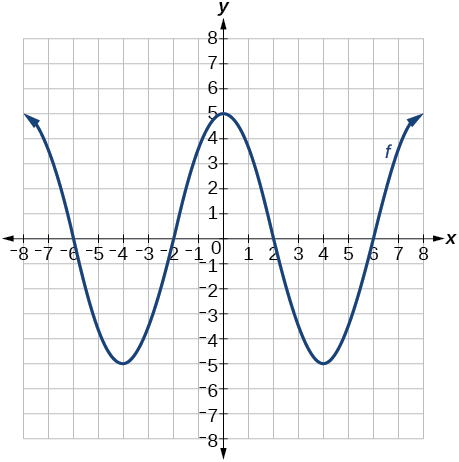
Gráfico de um polinômio.

78)$g(x)=f(x)−2$

79)$g(x)=−f(x)$

Responda

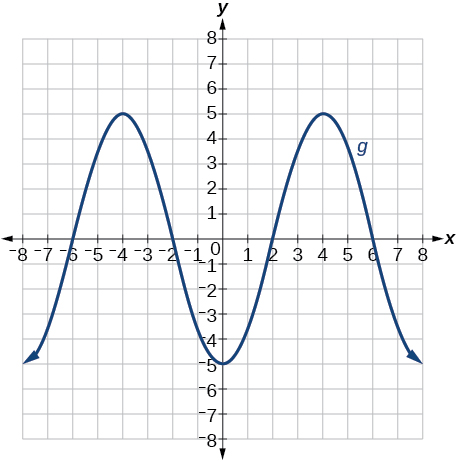
Gráfico de um polinômio.

80)$g(x)=f(x+1)$

81)$g(x)=f(x−2)$

Responda

Gráfico de um polinômio.

1.6: Funções de valor absoluto

As distâncias no universo podem ser medidas em todas as direções. Como tal, é útil considerar a distância como uma função de valor absoluto. Nesta seção, investigaremos as funções de valor absoluto. A função de valor absoluto é comumente considerada como fornecendo a distância entre o número e zero em uma reta numérica. Algebricamente, para qualquer que seja o valor de entrada, a saída é o valor sem levar em conta o sinal.

Verbal

1) Como você resolve uma equação de valor absoluto?

Responda

Isole o termo de valor absoluto para que a equação tenha a forma$|A|=B$. Forme uma equação definindo a expressão dentro do símbolo de valor absoluto$A$,, igual à expressão do outro lado da equação,$B$. Forme uma segunda equação definindo$A$ igual ao oposto da expressão no outro lado da equação,$−B$. Resolva cada equação para a variável.

2) Como você pode saber se uma função de valor absoluto tem dois$x$ interceptos sem representar graficamente a função?

3) Ao resolver uma função de valor absoluto, o termo de valor absoluto isolado é igual a um número negativo. O que isso diz sobre o gráfico da função de valor absoluto?

Responda

O gráfico da função de valor absoluto não cruza o$x$ eixo -, então o gráfico está completamente acima ou completamente abaixo do$x$ eixo -.

4) Como você pode usar o gráfico de uma função de valor absoluto para determinar os$x$ valores -para os quais os valores da função são negativos?

5) Como você resolve uma desigualdade de valor absoluto algebricamente?

Responda

Primeiro determine os pontos de limite encontrando a (s) solução (s) da equação. Use os pontos limite para formar possíveis intervalos de solução. Escolha um valor de teste em cada intervalo para determinar quais valores satisfazem a desigualdade.

Algébrico

6) Descreva todos os números$x$ que estão a uma$4$ distância do número$8$. Expresse isso usando notação de valor absoluto.

7) Descreva todos os números$x$ que estão a uma$\dfrac{1}{2}$ distância do número$-4$. Expresse isso usando notação de valor absoluto.

Responda

$|x+4|= \dfrac{1}{2}$

8) Descreva a situação em que a distância desse ponto$x$$10$ é de pelo menos$15$ unidades. Expresse isso usando notação de valor absoluto.

9) Encontre todos os valores da função de$f(x)$ forma que a distância de$f(x)$ até o valor$8$ seja menor que$0.03$ unidades. Expresse isso usando notação de valor absoluto.

Responda

$|f(x)−8|<0.03$

Para os exercícios 10-24, resolva as equações abaixo e expresse a resposta usando a notação de conjunto.

10)$|x+3|=9$

11)$|6−x|=5$

Responda

${1,11}$

12)$|5x−2|=11$

13)$|4x−2|=11$

Responda

$\left \{\dfrac{9}{4}, \dfrac{13}{4} \right \}$

14)$2|4−x|=7$

15)$3|5−x|=5$

Responda

$\left \{\dfrac{10}{3},\dfrac{20}{3} \right \}$

16)$3|x+1|−4=5$

17)$5|x−4|−7=2$

Responda

$\left \{\dfrac{11}{5}, \dfrac{29}{5} \right \}$

18)$0=−|x−3|+2$

19)$2|x−3|+1=2$

Responda

$\left \{\dfrac{5}{2}, \dfrac{7}{2} \right \}$

20)$|3x−2|=7$

21)$|3x−2|=−7$

Responda

Sem solução

22)$\left |\dfrac{1}{2}x−5 \right |=11$

23)$\left |\dfrac{1}{3}x+5 \right |=14$

Responda

$\{−57,27\}$

24)$−\left |\dfrac{1}{3}x+5 \right |+14=0$

Para os exercícios 25-28, encontre os$y$ interceptos$x$ - e -dos gráficos de cada função.

25)$f(x)=2|x+1|−10$

Responda

$(0,−8)$;$(−6,0)$,$(4,0)$

26)$f(x)=4|x−3|+4$

27)$f(x)=−3|x−2|−1$

Responda

$(0,−7)$;$x$ sem interceptações

28)$f(x)=−2|x+1|+6$

Para os exercícios 29-36, resolva cada desigualdade e escreva a solução em notação de intervalo.

29)$| x−2 |>10$

Responda

$(−\infty,−8)\cup(12,\infty)$

30)$2|v−7|−4\geq42$

31)$|3x−4|\geq8$

Responda

$−\dfrac{4}{3}{\leq}x\leq4$

32)$|x−4|\geq8$

33)$|3x−5|\geq-13$

Responda

$\left (−\infty,− \dfrac{8}{3}\right ]\cup\left[6,\infty\right)$

34)$|3x−5|\geq−13$

(35)$|\dfrac{3}{4}x−5|\geq7$

Responda

$\left (-\infty,-\dfrac{8}{3}\right ]\cup\left[16,\infty\right)$

36)$\left |\dfrac{3}{4}x−5 \right |+1\leq16$

Gráfica

Para os exercícios 37-39, represente graficamente a função de valor absoluto. Faça um gráfico de pelo menos cinco pontos manualmente para cada gráfico.

37)$y=|x−1|$

Responda

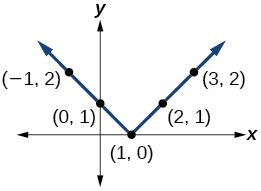
38)$y=|x+1|$

39)$y=|x|+1$

Responda

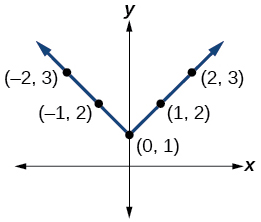
Para os exercícios 40-52, faça um gráfico manual das funções dadas.

40)$y=|x|−2$

41)$y=−|x|$

Responda

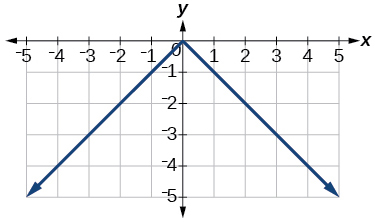
(42)$y=−|x|−2$

43)$y=−|x−3|−2$

Responda

44)$f(x)=−|x−1|−2$

45)$f(x)=−|x+3|+4$

Responda

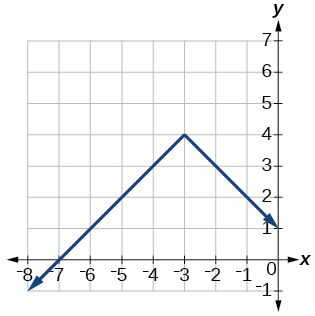
(46)$f(x)=2|x+3|+1$

47)$f(x)=3|x−2|+3$

Responda

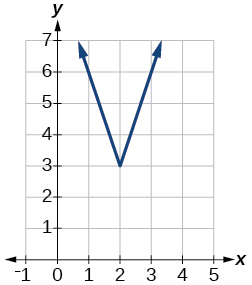
48)$f(x)=|2x−4|−3$

49)$f(x)=|3x+9|+2$

Responda

50)$f(x)=−|x−1|−3$

51)$f(x)=−|x+4|−3$

Responda

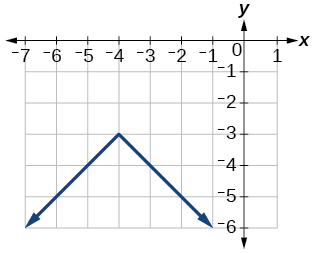
52)$f(x)=\dfrac{1}{2}|x+4|−3$

Tecnologia

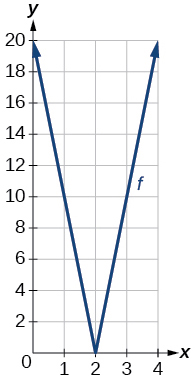
53) Use um utilitário gráfico para representar graficamente$f(x)=10|x−2|$ na janela de visualização$[0,4]$. Identifique o intervalo correspondente. Mostre o gráfico.

Responda

alcance:$[0,20]$

54) Use um utilitário gráfico para representar graficamente$f(x)=−100|x|+100$ na janela de visualização$[−5,5]$. Identifique o intervalo correspondente. Mostre o gráfico.

Para os exercícios 55-56, represente graficamente cada função usando um utilitário gráfico. Especifique a janela de visualização.

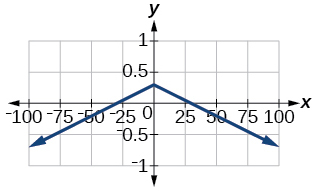
55)$f(x)=−0.1|0.1(0.2−x)|+0.3$

Responda

$x$-intercepta:

(56)$f(x)=4 \times10^{9}|x−(5 \times 10^9)|+2 \times10^9$

Extensões

Para os exercícios 57-59, resolva a desigualdade.

57)$\left |−2x− \dfrac{2}{3}(x+1) \right |+3>−1$

Responda

$(−\infty,\infty)$

58) Se possível, encontre todos os valores de a para os quais não haja$x$ interceptações$f(x)=2|x+1|+a$.

59) Se possível, encontre todos os valores de a para os quais não haja$y$ interceptações$f(x)=2|x+1|+a$.

Responda

Não há solução para a que impeça que a função tenha um$y$ intercepto. A função de valor absoluto sempre cruza o$y$ -intercept quando$x=0$.

Aplicativos do mundo real

60) As cidades A e B estão na mesma linha leste-oeste. Suponha que a cidade A esteja localizada na origem. Se a distância da cidade A até a cidade B for de pelo menos$100$ milhas e$x$ representar a distância da cidade B até a cidade A, expresse isso usando a notação de valor absoluto.

61) A verdadeira proporção$p$ de pessoas que atribuem uma classificação favorável ao Congresso está$8\%$ com uma margem de erro de$1.5\%$. Descreva essa afirmação usando uma equação de valor absoluto.

Responda

$|p−0.08|\leq0.015$

62) Os alunos que pontuarem dentro de$18$ pontos do número$82$ passarão em um teste específico. Escreva essa afirmação usando a notação de valor absoluto e use a variável$x$ para a pontuação.

63) Um maquinista deve produzir um rolamento que esteja dentro de$0.01$ polegadas do diâmetro correto de$5.0$ polegadas. Usando$x$ como diâmetro do rolamento, escreva essa declaração usando a notação de valor absoluto.

Responda

$|x−5.0|\leq0.01$

64) A tolerância para um rolamento de esferas é$0.01$. Se o diâmetro real do rolamento for$2.0$ polegadas e o valor medido do diâmetro for$x$ polegadas, expresse a tolerância usando a notação de valor absoluto.

1.7: Funções inversas

Se algumas máquinas físicas podem funcionar em duas direções, podemos perguntar se algumas das funções “máquinas” que estamos estudando também podem funcionar de forma inversa. Nesta seção, consideraremos a natureza inversa das funções.

Verbal

1) Descreva por que o teste de linha horizontal é uma forma eficaz de determinar se uma função é individual?

Responda

Cada saída de uma função deve ter exatamente uma saída para que a função seja individual. Se alguma linha horizontal cruzar o gráfico de uma função mais de uma vez, isso significa que$y$ os valores -se repetem e a função não é um para um. Se nenhuma linha horizontal cruzar o gráfico da função mais de uma vez, nenhum$y$ valor -se repetirá e a função será de um para um.

2) Por que restringimos o domínio da função$f(x)=x^2$ para encontrar o inverso da função?

3) Uma função pode ser sua própria inversa? Explique.

Responda

Sim. Por exemplo,$f(x)=\dfrac{1}{x}$ é seu próprio inverso.

4) As funções individuais estão sempre aumentando ou sempre diminuindo? Por que ou por que não?

5) Como você encontra o inverso de uma função algebricamente?

Responda

Dada uma função$y=f(x)$, resolva para$x$ em termos de$y$. Troque o$x$$y$ e. Resolva a nova equação para$y$. A expressão para$y$ é o inverso,$y=f^{-1}(x)$.

Algébrico

6) Mostre que a função$f(x)=a−x$ é sua própria inversa para todos os números reais$a$.

Para os exercícios 7-12, encontre$f^{-1}(x)$ para cada função.

7)$f(x)=x+3$

Responda

$f^{-1}(x)=x−3$

8)$f(x)=x+5$

9)$f(x)=2−x$

Responda

$f^{-1}(x)=2−x$

10)$f(x)=3−x$

11)$f(x)=\dfrac{x}{x+2}$

Responda

$f^{-1}(x)=\dfrac{−2x}{x−1}$

12)$f(x)=\dfrac{2x+3}{5x+4}$

Para os exercícios 13-16, encontre um domínio no qual cada função$f$ seja individual e não decrescente. Escreva o domínio em notação de intervalo. Em seguida, encontre o inverso de$f$ restrito a esse domínio.

13)$f(x)=(x+7)^2$

Responda

domínio de$f(x)$:$\left[−7,\infty\right)$;$f^{-1}(x)=\sqrt{x}−7$

14)$f(x)=(x−6)^2$

15)$f(x)=x^2−5$

Responda

domínio de$f(x)$:$\left[0,\infty\right)$;$f^{-1}(x)=\sqrt{x+5}$

16) Dado$f(x)=\dfrac{x}{2+x}$ e$g(x)=\dfrac{2x}{1-x}:$

1. Encontre$f(g(x))$$g(f(x))$ e.
2. O que a resposta nos diz sobre a relação entre$f(x)$ e$g(x)?$

Responda

a.$f(g(x))=x$ e$g(f(x))=x$

b. Isso nos diz que$f$ e$g$ são funções inversas

Para os exercícios 17-18, use a composição da função para verificar se$f(x)$$g(x)$ são funções inversas.

17)$f(x)=\sqrt[3]{x-1}$ e$g(x)=x^3+1$

Responda

$f(g(x))=x$,$g(f(x))=x$

18)$f(x)=−3x+5$ e$g(x)=\dfrac{x-5}{-3}$

Gráfica

Para os exercícios 19-22, use um utilitário gráfico para determinar se cada função é individual.

19)$f(x)=\sqrt{x}$

Responda

um para um

20)$f(x)=\sqrt[3]{3x+1}$

21)$f(x)=−5x+1$

Responda

um para um

22)$f(x)=x^3−27$

Para os exercícios 23-24, determine se o gráfico representa uma função individual.

23)

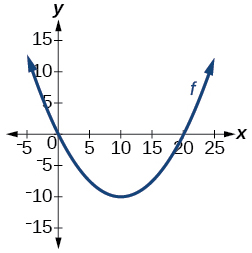
Responda

não um para um

24)

Figura abaixo.

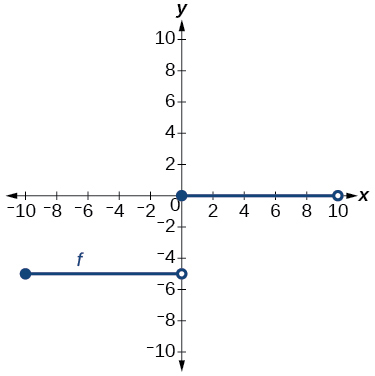
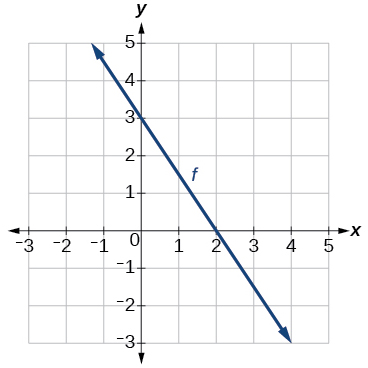
Gráfico de uma linha

25) Encontre$f(0)$.

Responda

$3$

26) Resolver$f(x)=0$.

27) Encontrar$f^{-1}(0)$.

Responda

$2$

28) Resolver$f^{-1}(x)=0$.

Para os exercícios 29-32, use o gráfico da função individual mostrada na Figura abaixo

Gráfico de uma função de raiz quadrada.

29) Esboce o gráfico de$f^{-1}$.

Responda

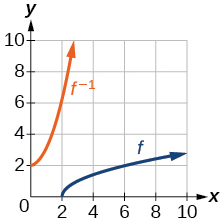
30) Encontre$f(6)$$f^{-1}(2)$ e.

31) Se o gráfico completo de$f$ for mostrado, encontre o domínio de$f$.

Responda

$[2,10]$

32) Se o gráfico completo de$f$ for mostrado, encontre o intervalo de$f$

Numérico

Para os exercícios 33-36, avalie ou resolva, assumindo que a função$f$ é individual.

33) Se$f(6)=7$, encontre$f^{-1}(7)$.

Responda

$6$

34) Se$f(3)=2$, encontre$f^{-1}(2)$.

35) Se$f^{-1}(−4)=−8$, encontre$f(−8)$.

Responda

$-4$

36) Se$f^{-1}(−2)$ =−1, encontre$f(−1)$.

Para os exercícios 37-40, use os valores listados na Tabela abaixo para avaliar ou resolver.

$x$	$f(x)$
\ (x\) ">0	\ (f (x)\) ">8
\ (x\) ">1	\ (f (x)\) ">0
\ (x\) ">2	\ (f (x)\) ">7
\ (x\) ">3	\ (f (x)\) ">4
\ (x\) ">4	\ (f (x)\) ">2
\ (x\) ">5	\ (f (x)\) ">6
\ (x\) ">6	\ (f (x)\) ">5
\ (x\) ">7	\ (f (x)\) ">3
\ (x\) ">8	\ (f (x)\) ">9
\ (x\) ">9	\ (f (x)\) ">1

37) Encontrar$f(1)$.

Responda

$0$

38) Resolver$f(x)=3$.

39) Encontrar$f^{-1}(0)$.

Responda

$1$

40) Resolver$f^{-1}(x)=7$.

41) Use a representação tabular de$f$ na Tabela abaixo para criar uma tabela para$f^{-1}(x)$.

$x$	3	6	9	13	14
$f(x)$	1	4	7	12	16

Responda

$x$	1	4	7	12	16
$f^{-1}(x)$	3	6	9	13	14

Tecnologia

Para os exercícios 42-44, encontre a função inversa. Em seguida, represente graficamente a função e seu inverso.

(42)$f(x)=\dfrac{3}{x-2}$

43)$f(x)=x^3−1$

Responda

$f^{-1}(x)=(1+x)^{1/3}$

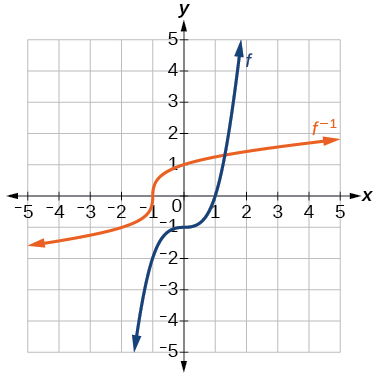
44) Encontre a função inversa de$f(x)=\dfrac{1}{x-1}$. Use um utilitário gráfico para encontrar seu domínio e alcance. Escreva o domínio e o intervalo em notação de intervalo.

Aplicativos do mundo real

45) Para converter de$x$ graus Celsius para$y$ graus Fahrenheit, usamos a fórmula$f(x)=\dfrac{9}{5}x+32$. Encontre a função inversa, se ela existir, e explique seu significado.

Responda

$f^{-1}(x)=\dfrac{5}{9}(x−32)$. Dada a temperatura em Fahrenheit$x$, essa fórmula permite calcular a temperatura Celsius.

46) A circunferência$C$ de um círculo é uma função de seu raio dado por$C(r)=2{\pi}r$. Expresse o raio de um círculo em função de sua circunferência. Chame essa função$r(C)$. Encontre$r(36\pi)$ e interprete seu significado.

47) Um carro viaja a uma velocidade constante de$50$ milhas por hora. A distância que o carro percorre em milhas é uma função do tempo,$t$, em horas, dado por$d(t)=50t$. Encontre a função inversa expressando o tempo de viagem em termos da distância percorrida. Chame essa função$t(d)$. Encontre$t(180)$ e interprete seu significado.

Responda

$t(d)=\dfrac{d}{50}$,$t(180)=\dfrac{180}{50}$. O tempo para o carro percorrer$180$ milhas é de$3.6$ horas.