1.7: Funções inversas

Last updated
Save as PDF

Page ID: 189196

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Verifique as funções inversas.
Determine o domínio e o alcance de uma função inversa e restrinja o domínio de uma função para torná-la individual.
Encontre ou avalie o inverso de uma função.
Use o gráfico de uma função um-para-um para representar graficamente sua função inversa nos mesmos eixos.

Uma bomba de calor reversível é um sistema de controle de temperatura que é um ar condicionado e um aquecedor em um único dispositivo. Operado em uma direção, ele bombeia calor para fora de uma casa para fornecer resfriamento. Operando ao contrário, ele bombeia calor para o prédio pelo lado de fora, mesmo em clima frio, para fornecer aquecimento. Como aquecedor, uma bomba de calor é várias vezes mais eficiente do que o aquecimento por resistência elétrica convencional.

Se algumas máquinas físicas puderem funcionar em duas direções, podemos perguntar se algumas das funções “máquinas” que estamos estudando também podem funcionar de forma inversa. A figura$\PageIndex{1}$ fornece uma representação visual dessa questão. Nesta seção, consideraremos a natureza inversa das funções.

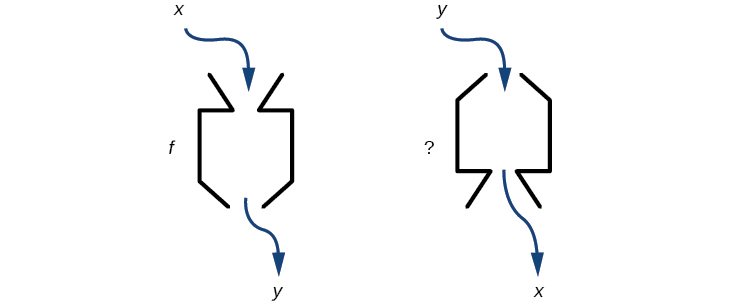
$Diagrama de uma função e seria seu inverso$
Figura$\PageIndex{1}$: Uma função “máquina” pode operar em sentido inverso?

Verificando se duas funções são funções inversas

Suponha que um estilista viajando para Milão para um desfile de moda queira saber qual será a temperatura. Ele não está familiarizado com a escala Celsius. Para ter uma ideia de como as medições de temperatura estão relacionadas, ele pede à sua assistente, Betty, que converta 75 graus Fahrenheit em graus Celsius. Ela encontra a fórmula

\[C=\dfrac{5}{9}(F−32)\]

e substitui 75 por$F$ para calcular

\[\dfrac{5}{9}(75−32)\approx24^{\circ}\]

Sabendo que um confortável 75 graus Fahrenheit tem cerca de 24 graus Celsius, ele envia a sua assistente a previsão do tempo da semana da Figure$\PageIndex{2}$ for Milan e pede que ela converta todas as temperaturas em graus Fahrenheit.

Figura$\PageIndex{2}$: Uma previsão do tempo de segunda a quinta-feira.

A princípio, Betty considera usar a fórmula que ela já encontrou para completar as conversões. Afinal, ela conhece sua álgebra e pode facilmente resolver a equação$F$ depois de substituir um valor por$C$. Por exemplo, para converter 26 graus Celsius, ela poderia escrever

\[\begin{align} 26&=\dfrac{5}{9}(F-32) \\ 26⋅\dfrac{9}{5}&=F−32 \\ F&=26⋅\dfrac{9}{5}+32\approx79\end{align}\]

Depois de considerar essa opção por um momento, no entanto, ela percebe que resolver a equação para cada uma das temperaturas será muito tedioso. Ela percebe que, como avaliar é mais fácil do que resolver, seria muito mais conveniente ter uma fórmula diferente, que meça a temperatura Celsius e produza a temperatura em Fahrenheit.

A fórmula pela qual Betty está procurando corresponde à ideia de uma função inversa, que é uma função para a qual a entrada da função original se torna a saída da função inversa e a saída da função original se torna a entrada da função inversa.

Dada uma função$f(x)$, representamos seu inverso como$f^{−1}(x)$, lido como “$f$inverso de”$x$. O −1 elevado faz parte da notação. Não é um expoente; não implica uma potência de −1. Em outras palavras, não$f^{−1}(x)$ significa$\frac{1}{f(x)}$ porque$\frac{1}{f(x)}$ é o inverso$f$ e não o inverso.

A notação “semelhante a um expoente” vem de uma analogia entre composição e multiplicação de funções: assim como$a^{−1}a=1$ (1 é o elemento de identidade para multiplicação) para qualquer número diferente de zero$a$, então é$f^{−1}{\circ}f$ igual à função de identidade, ou seja,

\[(f^{−1}{\circ}f)(x)=f^{−1}(f(x))=f^{−1}(y)=x\]

Isso vale para todos$x$ no domínio de$f$. Informalmente, isso significa que funções inversas “se desfazem” umas às outras. No entanto, assim como zero não tem um recíproco, algumas funções não têm inversas.

Dada uma função$f(x)$, podemos verificar se alguma outra função$g(x)$ é o inverso de$f(x)$ verificando se uma$g(f(x))=x$ ou$f(g(x))=x$ é verdadeira. Podemos testar qualquer equação com a qual seja mais conveniente trabalhar porque elas são logicamente equivalentes (ou seja, se uma for verdadeira, a outra também será).

Por exemplo,$y=4x$ e$y=\frac{1}{4}x$ são funções inversas.

\[(f^{−1}{\circ}f)(x)=f^{-1}(4x)=\dfrac{1}{4}(4x)=x\]

\[(f{\circ}f^{−1})(x)=f\Big(\dfrac{1}{4}x\Big)=4\Big(\dfrac{1}{4}x\Big)=x\]

Alguns pares de coordenadas do gráfico da função$y=4x$ são$(−2, −8)$$(0, 0)$,$(2, 8)$ e. Alguns pares de coordenadas do gráfico da função$y=\frac{1}{4}x$ são$(−8, −2)$$(0, 0)$,$(8, 2)$ e. Se trocarmos a entrada e a saída de cada par de coordenadas de uma função, os pares de coordenadas trocados apareceriam no gráfico da função inversa.

Definição: Função inversa

Para qualquer função individual$f(x)=y$, uma função$f^{−1}(x)$ é uma função inversa de$f$ if$f^{−1}(y)=x$. Isso também pode ser escrito como$f^{−1}(f(x))=x$ para todos$x$ no domínio de$f$. Também se segue que$f(f^{−1}(x))=x$ para todos$x$ no domínio de$f^{−1}$ if$f^{−1}$ é o inverso de$f$.

A notação$f^{−1}$ é lida como “$f$inversa”. Como qualquer outra função, podemos usar qualquer nome de variável como entrada para$f^{−1}$, então geralmente escrevemos$f^{−1}(x)$, o que lemos como “$f$inverso de”$x$. Tenha em mente que

\[f^{−1}(x)\neq\dfrac{1}{f(x)}\]

e nem todas as funções têm inversas.

Exemplo$\PageIndex{1}$: Identifying an Inverse Function for a Given Input-Output Pair

Se para uma função individual específica$f(2)=4$ e$f(5)=12$, quais são os valores de entrada e saída correspondentes para a função inversa?

Solução

A função inversa inverte as quantidades de entrada e saída, então se

\[f(2)=4, \text{ then } f^{-1}(4)=2 ;\\ f(5)=12, \text{ then }f^{-1}(12)=5\].

Como alternativa, se quisermos nomear a função inversa$g$, então$g(4)=2$$g(12)=5$ e.

Análise

Observe que, se mostrarmos os pares de coordenadas em forma de tabela, a entrada e a saída serão claramente invertidas. Veja a tabela$\PageIndex{1}$.

Tabela$\PageIndex{1}$
$(x,f(x))$	$(x,g(x))$
\ ((x, f (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">$(2,4)$	\ ((x, g (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">$(4,2)$
\ ((x, f (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">$(5,12)$	\ ((x, g (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">$(12,5)$

Exercício$\PageIndex{1}$

Diante disso$h^{-1}(6)=2$, quais são os valores de entrada e saída correspondentes da função original$h$?

Responda: $h(2)=6$

Como fazer: Dadas duas funções$f(x)$ and $g(x)$, test whether the functions are inverses of each other.

Determine se$f(g(x))=x$ ou$g(f(x))=x$.
Se ambas as afirmações forem verdadeiras, então$g=f^{-1}$$f=g^{-1}$ e. Se uma das afirmações for falsa, ambas serão falsas$g{\neq}f^{-1}$ e$f{\neq}g^{-1}$ e.

Exemplo$\PageIndex{2}$: Testing Inverse Relationships Algebraically

Se$f(x)=\frac{1}{x+2}$ e$g(x)=\frac{1}{x}−2$, é$g=f^{-1}$?

Solução

\[\begin{align} g(f(x))&=\dfrac{1}{(\frac{1}{x+2})−2} \\ &=x+2−2 \\&=x \end{align}\]

então

\[g=f^{-1} \text{ and } f=g^{-1}\]

Isso é suficiente para responder sim à pergunta, mas também podemos verificar a outra fórmula.

\[\begin{align} f(g(x))&=\dfrac{1}{\frac{1}{x}-2+2} \\ &= \dfrac{1}{\frac{1}{x}} \\ &=x \end{align}\]

Análise

Observe que as operações inversas estão na ordem inversa das operações da função original.

Exercício$\PageIndex{2}$

Se$f(x)=x^3−4$ e$g(x)=\sqrt[3]{x+4}$, é$g=f^{-1}$?

Responda: sim

Exemplo$\PageIndex{3}$: Determining Inverse Relationships for Power Functions

Se$f(x)=x^3$ (a função de cubo) e$g(x)=\frac{1}{3}x$, é$g=f^{-1}$?

Solução

\[f(g(x))=\dfrac{x^3}{27}{\neq}x\]

Não, as funções não são inversas.
Análise

O inverso correto do cubo é, obviamente, a raiz cúbica$\sqrt[3]{x}=x^{\frac{1}{3}}$, ou seja, um terço é um expoente, não um multiplicador.

Exercício$\PageIndex{3}$

Se$f(x)=(x−1)^3$ e$g(x)=\sqrt[3]{x}+1$, é$g=f^{-1}$?

Responda: sim

Encontrando o domínio e o intervalo de funções inversas

As saídas da função$f$ são as entradas para$f^{-1}$, então o intervalo de também$f$ é o domínio de$f^{-1}$. Da mesma forma, como as entradas para$f$ são as saídas de$f^{-1}$, o domínio de$f$ é o intervalo de$f^{-1}$. Podemos visualizar a situação como na Figura$\PageIndex{3}$.

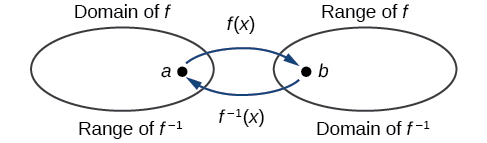
$Domínio e alcance de uma função e seu inverso.$
Figura$\PageIndex{3}$: Domínio e alcance de uma função e seu inverso.

Quando uma função não tem função inversa, é possível criar uma nova função em que essa nova função em um domínio limitado tenha uma função inversa. Por exemplo, o inverso de$f(x)=\sqrt{x}$ é$f^{-1}(x)=x^2$, porque um quadrado “desfaz” uma raiz quadrada; mas o quadrado é apenas o inverso da raiz quadrada no domínio$\left[0,\infty\right)$, já que esse é o intervalo de$f(x)=\sqrt{x}$.

Podemos analisar esse problema do outro lado, começando com a função quadrada (quadrática do kit de ferramentas)$f(x)=x^2$. Se quisermos construir um inverso a essa função, nos deparamos com um problema, porque para cada saída dada da função quadrática, há duas entradas correspondentes (exceto quando a entrada é 0). Por exemplo, a saída 9 da função quadrática corresponde às entradas 3 e —3. Mas uma saída de uma função é uma entrada para seu inverso; se essa entrada inversa corresponde a mais de uma saída inversa (entrada da função original), então o “inverso” não é uma função! Em outras palavras, a função quadrática não é uma função individual; ela falha no teste da linha horizontal e, portanto, não tem uma função inversa. Para que uma função tenha um inverso, ela deve ser uma função individual.

Em muitos casos, se uma função não for individual, ainda podemos restringi-la a uma parte de seu domínio na qual ela é individual. Por exemplo, podemos criar uma versão restrita da função quadrada$f(x)=x^2$ com seu alcance limitado a$\left[0,\infty\right)$, que é uma função individual (ela passa no teste da linha horizontal) e que tem um inverso (a função de raiz quadrada).

Se$f(x)=(x−1)^2$ ativada$[1,∞)$, a função inversa é$f^{-1}(x)=\sqrt{x}+1$.

O domínio de$f$ = intervalo de$f^{-1} = \left[1,\infty\right)$.
O domínio de$f^{-1}$ = intervalo de$f = \left[0,\infty\right)$.

$alt$ É possível que uma função tenha mais de um inverso?

Não. Se duas funções supostamente diferentes, digamos,$g$ e h, atendem à definição de serem inversas de outra função$f$, então você pode provar isso$g=h$. Acabamos de ver que algumas funções só têm inversas se restringirmos o domínio da função original. Nesses casos, pode haver mais de uma maneira de restringir o domínio, levando a diferentes inversas. No entanto, em qualquer domínio, a função original ainda tem apenas um inverso exclusivo.

Nota: Domínio e faixa de funções inversas

O intervalo de uma função$f(x)$ é o domínio da função inversa$f^{-1}(x)$.

O domínio de$f(x)$ é o intervalo de$f^{-1}(x)$.

Como fazer: Dada uma função, encontre o domínio e o alcance de seu inverso.

Se a função for um para um, escreva o intervalo da função original como o domínio do inverso e escreva o domínio da função original como o intervalo do inverso.
Se o domínio da função original precisar ser restrito para torná-lo individual, esse domínio restrito se tornará o alcance da função inversa.

Exemplo$\PageIndex{4}$: Finding the Inverses of Toolkit Functions

Identifique quais das funções do kit de ferramentas, além da função quadrática, não são individuais e encontre um domínio restrito no qual cada função seja individual, se houver. As funções do kit de ferramentas são analisadas na Tabela$\PageIndex{2}$. Nós restringimos o domínio de tal forma que a função assume todos os valores y exatamente uma vez.

Tabela$\PageIndex{2}$
Constante	Identidade	Quadrático	Cúbico	Recíproco
$f(x)=c$	$f(x)=x$	$f(x)=x^2$	$f(x)=x^3$	$f(x)=\frac{1}{x}$
Quadrado recíproco	Raiz cúbica	raiz quadrada	Valor absoluto
$f(x)=\frac{1}{x^2}$	$f(x)=\sqrt[3]{x}$	$f(x)=\sqrt{x}$	$f(x)=\|x\|$

Solução

A função constante não é de um para um e não há domínio (exceto um único ponto) no qual ela possa ser um para um, então a função constante não tem inverso significativo.

A função de valor absoluto pode ser restrita ao domínio$\left[0,\infty\right)$, onde é igual à função de identidade.

A função quadrada recíproca pode ser restrita ao domínio$(0,\infty)$.

Análise

Podemos ver que essas funções (se irrestritas) não são individuais observando seus gráficos, mostrados na Figura$\PageIndex{4}$. Ambos falhariam no teste da linha horizontal. No entanto, se uma função estiver restrita a um determinado domínio para passar no teste da linha horizontal, nesse domínio restrito, ela poderá ter um inverso.

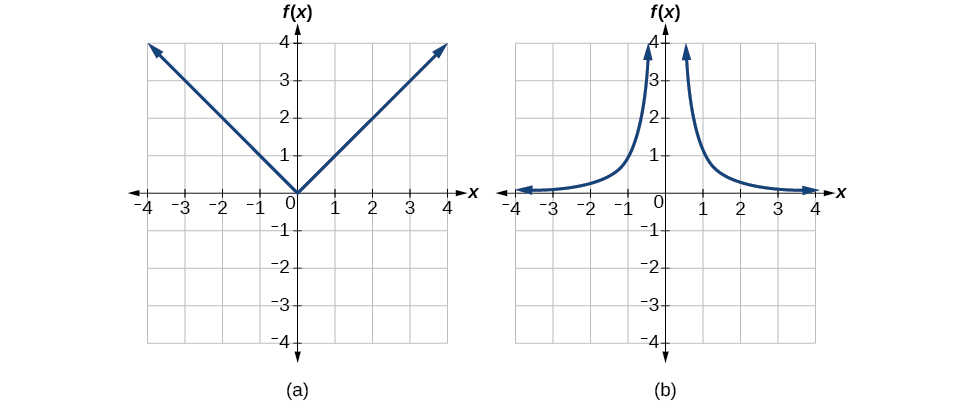
$Gráfico de uma função absoluta.$
Figura$\PageIndex{4}$: (a) Valor absoluto (b) Quadrado recíproco

$alt$ $\PageIndex{4}$: O domínio da função$f$ é$(1,\infty)$ e o intervalo da função$f$ é$(−\infty,−2)$. Encontre o domínio e o alcance da função inversa.

Solução

O domínio da função$f^{-1}$ é$(−\infty,−2)$ e o intervalo da função$f^{-1}$ é$(1,\infty)$.

Encontrando e avaliando funções inversas

Uma vez que temos uma função um-para-um, podemos calcular seu inverso em entradas específicas da função inversa ou construir uma representação completa da função inversa em muitos casos.

Invertendo funções tabulares

Suponha que desejemos encontrar o inverso de uma função representada em forma de tabela. Lembre-se de que o domínio de uma função é o intervalo do inverso e o alcance da função é o domínio do inverso. Portanto, precisamos trocar o domínio e o alcance.

Cada linha (ou coluna) de entradas se torna a linha (ou coluna) de saídas para a função inversa. Da mesma forma, cada linha (ou coluna) de saídas se torna a linha (ou coluna) de entradas para a função inversa.

Exemplo$\PageIndex{5}$: Interpreting the Inverse of a Tabular Function

Uma função$f(t)$ é dada na Tabela$\PageIndex{3}$, mostrando a distância em milhas que um carro percorreu em$t$ minutos. Encontre e interprete$f^{-1}(70)$

Tabela$\PageIndex{3}$
$t$(minutos)	30	50	70	90
$f(t)$(milhas)	20	40	60	70

A função inversa recebe uma saída de$f$ e retorna uma entrada para$f$. Então, na expressão$f^{-1}(70)$, 70 é um valor de saída da função original, representando 70 milhas. O inverso retornará a entrada correspondente da função original$f$, 90 minutos, então$f^{-1}(70)=90$. A interpretação disso é que, para dirigir 70 milhas, foram necessários 90 minutos.

Como alternativa, lembre-se de que a definição do inverso era se$f(a)=b$, então$f^{-1}(b)=a$. Por essa definição, se nos for dada$f^{-1}(70)=a$, então estamos procurando um valor$a$ para que$f(a)=70$. Nesse caso, estamos procurando um para$t$ que$f(t)=70$, que é quando$t=90$.

Exercício$\PageIndex{5}$

Usando Tabela$\PageIndex{4}$, encontre e interprete (a)$f(60)$ e (b)$f^{-1}(60)$.

Tabela$\PageIndex{4}$
$t$(minutos)	30	50	60	70	90
$f(t)$(milhas)	20	40	50	60	70

Responda: $f(60)=50$. Em 60 minutos, 50 milhas são percorridas.
$f^{-1}(60)=70$. Para viajar 60 milhas, levará 70 minutos.

Calculando o inverso de uma função, dado um gráfico da função original

Vimos em Funções e Notação de Função que o domínio de uma função pode ser lido observando a extensão horizontal de seu gráfico. Encontramos o domínio da função inversa observando a extensão vertical do gráfico da função original, porque isso corresponde à extensão horizontal da função inversa. Da mesma forma, encontramos o alcance da função inversa observando a extensão horizontal do gráfico da função original, pois essa é a extensão vertical da função inversa. Se quisermos calcular uma função inversa, encontramos sua entrada dentro de seu domínio, que é todo ou parte do eixo vertical do gráfico da função original.

$alt$ Dado o gráfico de uma função, calcule seu inverso em pontos específicos.

Encontre a entrada desejada no eixo y do gráfico fornecido.
Leia a saída da função inversa do eixo x do gráfico fornecido.

Exemplo$\PageIndex{6}$: Evaluating a Function and Its Inverse from a Graph at Specific Points

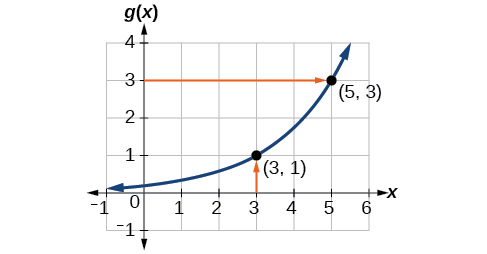
Uma função$g(x)$ é fornecida na Figura$\PageIndex{5}$. Encontre$g(3)$$g^{-1}(3)$ e.
.

Gráfico de <span translate= — Figura$\PageIndex{5}$: Gráfico de$g(x)$

Solução

Para avaliar$g(3)$, encontramos 3 no eixo x e encontramos o valor de saída correspondente no eixo y. O ponto nos$(3,1)$ diz isso$g(3)=1$.

Para avaliar$g^{-1}(3)$, lembre-se de que, por definição,$g^{-1}(3)$ significa o valor de$x$ para o qual$g(x)=3$. Ao procurar o valor de saída 3 no eixo vertical, encontramos o ponto$(5,3)$ no gráfico, o que significa, então$g(5)=3$, por definição,$g^{-1}(3)=5.$ Veja a Figura$\PageIndex{6}$.

gráfico de g (x) — Figura$\PageIndex{6}$: Gráfico de$g(x)$.

Exercício$\PageIndex{6}$

Usando o gráfico na Figura$\PageIndex{6}$, (a) encontre$g^{-1}(1)$ e (b) estime$g^{-1}(4)$.

Responda a: 3
Resposta b: 5.6

Encontrando inversas de funções representadas por fórmulas

Às vezes, precisaremos conhecer uma função inversa para todos os elementos de seu domínio, não apenas alguns. Se a função original for dada como uma fórmula - por exemplo,$y$ como uma função de$x$ -, muitas vezes podemos encontrar a função inversa resolvendo para obter$x$ como uma função de$y$.

Como fazer: Dada uma função representada por uma fórmula, encontre o inverso.

Certifique-se de que$f$ é uma função individual.
Resolver para$x$
Intercâmbio$x$$y$ e.

Exemplo$\PageIndex{7}$: Inverting the Fahrenheit-to-Celsius Function

Encontre uma fórmula para a função inversa que forneça a temperatura em Fahrenheit em função da temperatura Celsius.

\[C=\dfrac{5}{9}(F−32)\]

Solução

\[\begin{align} C&=\frac{5}{9}(F-32) \\ C{\cdot}\frac{9}{5}&=F−32 \\ F&=\frac{9}{5}C+32\end{align}\]

Ao resolver em geral, descobrimos a função inversa. E se

\[C=h(F)=\dfrac{5}{9}(F−32)\],

depois

\[F=h^{-1}(C)=\dfrac{9}{5}C+32.\]

Nesse caso, introduzimos uma função$h$ para representar a conversão porque as variáveis de entrada e saída são descritivas e a escrita$C^{-1}$ pode ser confusa.

Exercício$\PageIndex{7}$

Resolver por$x$ em termos de$y$ dados$y=\frac{1}{3}(x−5)$

Responda: $x=3y+5$

Exemplo$\PageIndex{8}$: Solving to Find an Inverse Function

Encontre o inverso da função$f(x)=\frac{2}{x−3}+4$.

Solução

\[\begin{align} y&=\dfrac{2}{x−3+4} &\text{Set up an equation.} \\ y−4&=\dfrac{2}{x−3} &\text{Subtract 4 from both sides.} \\ x−3&=\dfrac{2}{y−4} &\text{Multiply both sides by x−3 and divide by y−4.} \\ x&=\dfrac{2}{y−4}+3 &\text{Add 3 to both sides.} \end{align}\]

Então$f^{-1}(y)=\frac{2}{y−4}+3$ ou$f^{-1}(x)=\frac{2}{x−4}+3$.

Análise

O domínio e o intervalo de$f$ excluem os valores 3 e 4, respectivamente. $f$e$f^{-1}$ são iguais em dois pontos, mas não são a mesma função, como podemos ver ao criar uma tabela$\PageIndex{5}$.

Tabela$\PageIndex{5}$
$x$	1	2	5	$f^{-1}(y)$
$f(x)$	3	2	5	$y$

Exemplo$\PageIndex{9}$: Solving to Find an Inverse with Radicals

Encontre o inverso da função$f(x)=2+\sqrt{x−4}$.

Solução

\[ \begin{align} y&=2+\sqrt{x-4} \\ (y-2)^2&=x-4 \\ x&=(y-2)^2+4 \end{align}\]

Então$f^{-1}(x)=(x−2)^2+4$.

O domínio de$f$ é$\left[4,\infty\right)$. Observe que o intervalo de$f$ é$\left[2,\infty\right)$, então isso significa que o domínio da função inversa também$f^{-1}$ é$\left[2,\infty\right)$

Análise

A fórmula que encontramos$f^{-1}(x)$ parece ser válida para todos os reais$x$. No entanto,$f^{-1}$ em si deve ter um inverso (ou seja,$f$), então temos que restringir o domínio de$f^{-1}$ a para fazer$f^{-1}$ uma função individual.$\left[2,\infty\right)$ Esse domínio de$f^{-1}$ é exatamente o intervalo de$f$.

Exercício$\PageIndex{8}$

Qual é o inverso da função$f(x)=2-\sqrt{x}$? Indique os domínios da função e da função inversa.

Responda: $f^{-1}(x)=(2−x)^2$; domínio de$f$:$\left[0,\infty\right)$; domínio de$f^{-1}$:$\left(−\infty,2\right]$

Encontrando funções inversas e seus gráficos

Agora que podemos encontrar o inverso de uma função, exploraremos os gráficos das funções e seus inversos. Vamos retornar à função quadrática$f(x)=x^2$ restrita ao domínio$\left[0,\infty\right)$, no qual essa função é individual, e representá-la graficamente como na Figura$\PageIndex{7}$.

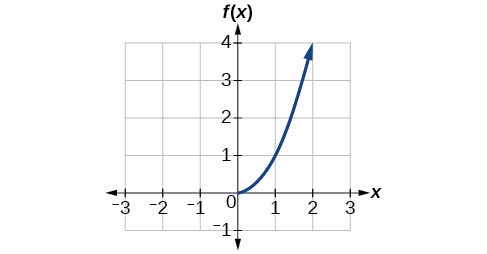
$Gráfico de f (x).$
Figura$\PageIndex{7}$: Função quadrática com domínio restrito$[0, \infty)$ a.

Restringir o domínio$\left[0,\infty\right)$ torna a função um para um (obviamente ela passará no teste da linha horizontal), então ela tem um inverso nesse domínio restrito.

Já sabemos que o inverso da função quadrática do kit de ferramentas é a função de raiz quadrada, ou seja,$f^{-1}(x)=\sqrt{x}$. O que acontece se representarmos graficamente os dois$f$ e$f^{-1}$ no mesmo conjunto de eixos, usando o eixo x para a entrada de ambos$f$ e$f^{-1}$?

Percebemos uma relação distinta: O gráfico de$f^{-1}(x)$ é o gráfico$f(x)$ refletido sobre a linha diagonal$y=x$, que chamaremos de linha de identidade, mostrado na Figura$\PageIndex{8}$.

\ (f (x)\)$f^(-1)(x)$ e. "src=” https://math.libretexts.org/@api/dek..._01_07_009.jpg "/>.
Figura$\PageIndex{8}$: Funções de raiz quadrada e quadrada no domínio não negativo

Essa relação será observada para todas as funções individuais, porque é resultado da função e de sua troca inversa de entradas e saídas. Isso equivale a trocar as funções dos eixos vertical e horizontal.

Exemplo$\PageIndex{10}$: Finding the Inverse of a Function Using Reflection about the Identity Line

Dado o gráfico de$f(x)$ na Figura$\PageIndex{9}$, esboce um gráfico de$f^{-1}(x)$.

Essa é uma função individual, então poderemos esboçar um inverso. Observe que o gráfico mostrado tem um domínio aparente de$(0,\infty)$ e uma faixa de$(−\infty,\infty)$, então o inverso terá um domínio$(−\infty,\infty)$ e uma faixa de$(0,\infty)$.

Se refletirmos esse gráfico sobre a linha$y=x$, o ponto$(1,0)$ refletirá para$(0,1)$ e o ponto$(4,2)$ refletirá para$(2,4)$. Esboçar o inverso nos mesmos eixos do gráfico original fornece a Figura$\PageIndex{10}$.

Exercício$\PageIndex{1}$

Desenhe gráficos das funções$f$ e$f^{-1}$ do Example$\PageIndex{8}$.

Responda: \ (f (x)\)$f^(-1)(x)$ e.” src=” https://math.libretexts.org/@api/dek..._01_07_012.jpg "/>
Figura$\PageIndex{11}$: Gráfico de$f(x)$$f^(-1)(x)$ e.

$alt$ Existe alguma função que seja igual ao seu próprio inverso?

Sim. Se$f=f^{-1}$, então$f(f(x))=x$, podemos pensar em várias funções que têm essa propriedade. A função de identidade

faz, assim como a função recíproca, porque

\[\dfrac{1}{\frac{1}{x}}=x\]

Qualquer função$f(x)=c−x$, onde$c$ é uma constante, também é igual ao seu próprio inverso.

Conceitos-chave

Se$g(x)$ for o inverso de$f(x)$, então$g(f(x))=f(g(x))=x$.
Cada uma das funções do kit de ferramentas tem um inverso.
Para que uma função tenha um inverso, ela deve ser individual (passar no teste da linha horizontal).
Uma função que não seja individual em todo o domínio pode ser individual em parte de seu domínio.
Para uma função tabular, troque as linhas de entrada e saída para obter o inverso.
O inverso de uma função pode ser determinado em pontos específicos em seu gráfico.
Para encontrar o inverso de uma fórmula, resolva a equação$y=f(x)$ para$x$ em função de$y$. Em seguida, troque os rótulos$x$$y$ e.
O gráfico de uma função inversa é o reflexo do gráfico da função original na linha$y=x$.

\((x,f(x))\)	\((x,g(x))\)
\ ((x, f (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">\((2,4)\)	\ ((x, g (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">\((4,2)\)
\ ((x, f (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">\((5,12)\)	\ ((x, g (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro; ">\((12,5)\)

\(x\)	1	2	5	\(f^{-1}(y)\)
\(f(x)\)	3	2	5	\(y\)

Constante	Identidade	Quadrático	Cúbico	Recíproco
\(f(x)=c\)	\(f(x)=x\)	\(f(x)=x^2\)	\(f(x)=x^3\)	\(f(x)=\frac{1}{x}\)
Quadrado recíproco	Raiz cúbica	raiz quadrada	Valor absoluto
\(f(x)=\frac{1}{x^2}\)	\(f(x)=\sqrt[3]{x}\)	\(f(x)=\sqrt{x}\)	\(f(x)=\|x\|\)

Tabela\(\PageIndex{3}\)
\(t\)(minutos)	30	50	70	90
\(f(t)\)(milhas)	20	40	60	70

Tabela\(\PageIndex{4}\)
\(t\)(minutos)	30	50	60	70	90
\(f(t)\)(milhas)	20	40	50	60	70