6.9: Ajustando modelos exponenciais aos dados
- Page ID
- 189420
- Crie um modelo exponencial a partir de dados.
- Crie um modelo logarítmico a partir de dados.
- Crie um modelo logístico a partir de dados.
Nas seções anteriores deste capítulo, ou recebemos uma função explicitamente para representar graficamente ou calcular, ou recebemos um conjunto de pontos que estavam garantidos na curva. Em seguida, usamos álgebra para encontrar a equação que se ajusta exatamente aos pontos. Nesta seção, usamos uma técnica de modelagem chamada análise de regressão para encontrar uma curva que modela dados coletados de observações do mundo real. Com a análise de regressão, não esperamos que todos os pontos estejam perfeitamente na curva. A ideia é encontrar um modelo que melhor se ajuste aos dados. Em seguida, usamos o modelo para fazer previsões sobre eventos futuros.
Não se confunda com a palavra modelo. Em matemática, costumamos usar os termos função, equação e modelo de forma intercambiável, mesmo que cada um tenha sua própria definição formal. O termo modelo é normalmente usado para indicar que a equação ou função se aproxima de uma situação do mundo real.
Vamos nos concentrar em três tipos de modelos de regressão nesta seção: exponencial, logarítmico e logístico. Já ter trabalhado com cada uma dessas funções nos dá uma vantagem. Conhecer suas definições formais, o comportamento de seus gráficos e algumas de suas aplicações no mundo real nos dá a oportunidade de aprofundar nosso entendimento. À medida que cada modelo de regressão é apresentado, as principais características e definições de sua função associada são incluídas para revisão. Reserve um momento para repensar cada uma dessas funções, refletir sobre o trabalho que fizemos até agora e depois explore as formas como a regressão é usada para modelar fenômenos do mundo real.
Construindo um modelo exponencial a partir de dados
Como aprendemos, há uma infinidade de situações que podem ser modeladas por funções exponenciais, como crescimento do investimento, decaimento radioativo, mudanças na pressão atmosférica e temperaturas de um objeto de resfriamento. O que esses fenômenos têm em comum? Por um lado, todos os modelos aumentam ou diminuem à medida que o tempo avança. Mas essa não é toda a história. É a forma como os dados aumentam ou diminuem que nos ajuda a determinar se eles são melhor modelados por uma equação exponencial. Conhecer o comportamento das funções exponenciais em geral nos permite reconhecer quando usar a regressão exponencial, então vamos revisar o crescimento e a decadência exponenciais.
Lembre-se de que as funções exponenciais têm a forma\(y=ab^x\) ou\(y=A_0e^{kx}\). Ao realizar a análise de regressão, usamos o formulário mais comumente usado em utilitários gráficos,\(y=ab^x\). Reserve um momento para refletir sobre as características que já aprendemos sobre a função exponencial\(y=ab^x\) (suponha\(a>0\)):
- \(b\)deve ser maior que zero e não igual a um.
- O valor inicial do modelo é\(y=a\).
- Se\(b>1\), a função modela o crescimento exponencial. À medida que\(x\) aumenta, as saídas do modelo aumentam lentamente no início, mas depois aumentam cada vez mais rapidamente, sem limites.
- Se\(0<b<1\), a função modela o decaimento exponencial. À medida que\(x\) aumenta, as saídas do modelo diminuem rapidamente no início e depois se nivelam para se tornarem assintóticas em relação ao eixo x. Em outras palavras, as saídas nunca se tornam iguais ou menores que zero.
Como parte dos resultados, sua calculadora exibirá um número conhecido como coeficiente de correlação, rotulado pela variável\(r\), ou\(r^2\). (Talvez seja necessário alterar as configurações da calculadora para que elas sejam mostradas.) Os valores são uma indicação da “qualidade do ajuste” da equação de regressão aos dados. Usamos mais comumente o valor de\(r^2\) em vez de\(r\), mas quanto mais próximo um dos valores estiver\(1\), melhor a equação de regressão se aproxima dos dados.
A regressão exponencial é usada para modelar situações em que o crescimento começa lentamente e depois acelera rapidamente sem limites, ou onde a decadência começa rapidamente e depois desacelera para chegar cada vez mais perto de zero. Usamos o comando “ExpReg” em um utilitário gráfico para ajustar uma função exponencial a um conjunto de pontos de dados. Isso retorna uma equação da forma,
\[y=ab^x\]
Observe que:
- \(b\)não deve ser negativo.
- quando\(b>1\), temos um modelo de crescimento exponencial.
- quando\(0<b<1\), temos um modelo de decaimento exponencial.
- Use o menu STAT e EDIT para inserir dados fornecidos.
- Limpe todos os dados existentes das listas.
- Liste os valores de entrada na coluna L1.
- Liste os valores de saída na coluna L2.
- Faça um gráfico e observe um gráfico de dispersão dos dados usando o recurso STATPLOT.
- Use ZOOM [9] para ajustar os eixos para se ajustarem aos dados.
- Verifique se os dados seguem um padrão exponencial.
- Encontre a equação que modela os dados.
- Selecione “ExpReg” no menu STAT e depois CALC.
- Use os valores retornados para a e b para registrar o modelo,\(y=ab^x\).
- Faça um gráfico do modelo na mesma janela do gráfico de dispersão para verificar se ele é um bom ajuste para os dados.
Exemplo\(\PageIndex{1}\): Using Exponential Regression to Fit a Model to Data
Em 2007, um estudo universitário foi publicado investigando o risco de acidente de dirigir sem álcool. Os dados de\(2,871\) acidentes foram usados para medir a associação do nível de álcool no sangue (BAC) de uma pessoa com o risco de sofrer um acidente. A tabela\(\PageIndex{1}\) mostra os resultados do estudo. O risco relativo é uma medida de quantas vezes mais chances uma pessoa tem de cair. Então, por exemplo, uma pessoa com um BAC de\(0.09\) tem\(3.54\) vezes mais probabilidade de cair do que uma pessoa que não bebeu álcool.
| DE VOLTA | 0 | 0,01 | 0,03 | 0,05 | 0,07 | 0,09 |
|---|---|---|---|---|---|---|
| Risco relativo de colisão | 1 | 1,03 | 1,06 | 1,38 | 2.09 | 3,54 |
| DE VOLTA | 0,11 | 0,13 | 0,15 | 0,17 | 0,19 | 0,21 |
| Risco relativo de colisão | 6.41 | 12,6 | 22.1 | 39,05 | 65,32 | 99,78 |
- Vamos\(x\) representar o nível de BAC e vamos\(y\) representar o risco relativo correspondente. Use a regressão exponencial para ajustar um modelo a esses dados.
- Depois de\(6\) beber, uma pessoa pesando\(160\) libras terá um BAC de cerca de\(0.16\). Quantas vezes é mais provável que uma pessoa com esse peso bata se dirigir depois de tomar um\(6\) pacote de cerveja? Arredonde para o centésimo mais próximo.
Solução
- Usando o menu STAT e EDIT em um utilitário gráfico, liste os valores de BAC em L1 e os valores de risco relativo em L2. Em seguida, use o recurso STATPLOT para verificar se o gráfico de dispersão segue o padrão exponencial mostrado na Figura\(\PageIndex{1}\):
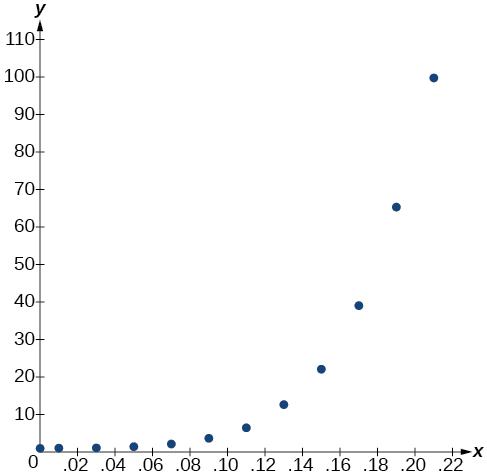
Figura\(\PageIndex{1}\)
Use o comando “ExpReg” do menu STAT e depois CALC para obter o modelo exponencial,
\(y=0.58304829{(2.20720213E10)}^x\)
Convertendo a partir da notação científica, temos:
\(y=0.58304829{(22,072,021,300)}^x\)
Observe o\(r^2≈0.97\) que indica que o modelo é uma boa opção para os dados. Para ver isso, represente graficamente o modelo na mesma janela do gráfico de dispersão para verificar se ele é um bom ajuste, conforme mostrado na Figura\(\PageIndex{2}\):
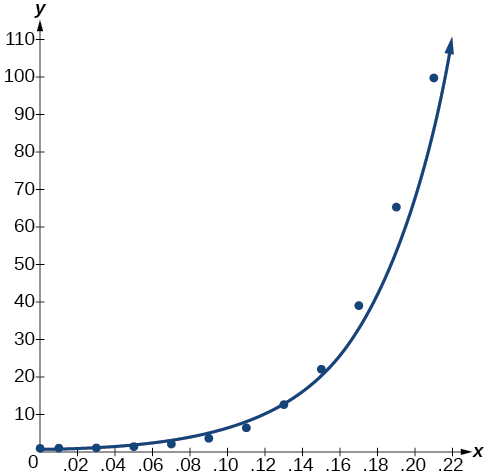
Figura\(\PageIndex{2}\)
- Use o modelo para estimar o risco associado a um BAC de\(0.16\). Substitua\(0.16\) por\(x\) no modelo e resolva por\(y\).
\[\begin{align*} y&= 0.58304829{(22,072,021,300)}^x \qquad \text{Use the regression model found in part } (a)\\ &= 0.58304829{(22,072,021,300)}^{0.16} \qquad \text{Substitute 0.16 for x}\\ &\approx 26.35 \qquad \text{Round to the nearest hundredth} \end{align*}\]
Se uma pessoa\(160\) de 1 quilo dirige depois de\(6\) beber, ela tem cerca de\(26.35\) duas vezes mais chances de bater do que dirigindo sóbria.
A tabela\(\PageIndex{2}\) mostra o saldo do cartão de crédito de um recém-formado todos os meses após a formatura.
| Mês | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Dívida ($) | 620,00 | 761,88 | 899,80 | 1039,93 | 1270,63 | 1589,04 | 1851,31 | 2154,92 |
- Use a regressão exponencial para ajustar um modelo a esses dados.
- Se os gastos continuarem nesse ritmo, qual será a dívida do cartão de crédito do graduado um ano após a graduação?
- Responda a um
-
O modelo de regressão exponencial que se ajusta a esses dados é\(y=522.88585984{(1.19645256)}^x\).
- Resposta b
-
Se os gastos continuarem nesse ritmo, a dívida do cartão de crédito do graduado será\($4,499.38\) após um ano.
Não. Lembre-se de que os modelos são formados por dados do mundo real coletados para regressão. Geralmente, é razoável fazer estimativas dentro do intervalo da observação original (interpolação). No entanto, quando um modelo é usado para fazer previsões, é importante usar habilidades de raciocínio para determinar se o modelo faz sentido para entradas muito além do intervalo de observação original (extrapolação).
Construindo um modelo logarítmico a partir de dados
Assim como nas funções exponenciais, existem muitas aplicações reais para funções logarítmicas: intensidade do som, níveis de pH das soluções, rendimentos de reações químicas, produção de bens e crescimento de bebês. Assim como nos modelos exponenciais, os dados modelados por funções logarítmicas estão sempre aumentando ou sempre diminuindo à medida que o tempo avança. Novamente, é a forma como eles aumentam ou diminuem que nos ajuda a determinar se um modelo logarítmico é o melhor.
Lembre-se de que as funções logarítmicas aumentam ou diminuem rapidamente no início, mas depois diminuem constantemente com o passar do tempo. Ao refletir sobre as características que já aprendemos sobre essa função, podemos analisar melhor as situações do mundo real que refletem esse tipo de crescimento ou decadência. Ao realizar a análise de regressão logarítmica, usamos a forma da função logarítmica mais comumente usada em utilitários gráficos,\(y=a+b\ln(x)\). Para esta função
- Todos os valores de entrada\(x\),, devem ser maiores que zero.
- O ponto\((1,a)\) está no gráfico do modelo.
- Se\(b>0\) sim, o modelo está aumentando. O crescimento aumenta rapidamente no início e depois diminui constantemente com o tempo.
- Se\(b<0\) sim, o modelo está diminuindo. A deterioração ocorre rapidamente no início e depois diminui constantemente com o tempo.
A regressão logarítmica é usada para modelar situações em que o crescimento ou a decadência aceleram rapidamente no início e depois diminuem com o tempo. Usamos o comando “LNReg” em um utilitário gráfico para ajustar uma função logarítmica a um conjunto de pontos de dados. Isso retorna uma equação da forma,
\[y=a+b\ln(x)\]
Note que
- todos os valores de entrada\(x\),, não devem ser negativos.
- quando\(b>0\), o modelo está aumentando.
- quando\(b<0\), o modelo está diminuindo.
- Use o menu STAT e EDIT para inserir dados fornecidos.
- Limpe todos os dados existentes das listas.
- Liste os valores de entrada na coluna L1.
- Liste os valores de saída na coluna L2.
- Faça um gráfico e observe um gráfico de dispersão dos dados usando o recurso STATPLOT.
- Use ZOOM [9] para ajustar os eixos para se ajustarem aos dados.
- Verifique se os dados seguem um padrão logarítmico.
- Encontre a equação que modela os dados.
- Selecione “LNReg” no menu STAT e depois CALC.
- Use os valores retornados para a e b para registrar o modelo,\(y=a+b\ln(x)\).
- Faça um gráfico do modelo na mesma janela do gráfico de dispersão para verificar se ele é um bom ajuste para os dados.
Devido aos avanços da medicina e aos padrões de vida mais elevados, a expectativa de vida vem aumentando na maioria dos países desenvolvidos desde o início do século XX. A tabela\(\PageIndex{3}\) mostra a expectativa média de vida, em anos, dos americanos de 1900 a 2010.
| Ano | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 |
|---|---|---|---|---|---|---|
| Expectativa de vida (anos) | 47,3 | 50,0 | 54.1 | 59,7 | 62,9 | 68,2 |
| Ano | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
| Expectativa de vida (anos) | 69,7 | 70,8 | 73,7 | 75,4 | 76,8 | 78,7 |
- Vamos\(x\) representar o tempo em décadas, começando com\(x=1\) o ano de 1900,\(x=2\) para o ano de 1910 e assim por diante. Vamos\(y\) representar a expectativa de vida correspondente. Use a regressão logarítmica para ajustar um modelo a esses dados.
- Use o modelo para prever a expectativa média de vida americana para o ano de 2030.
Solução
- Usando o menu STAT e EDIT em um utilitário gráfico, liste os anos usando valores\(1–12\) em L1 e a expectativa de vida correspondente em L2. Em seguida, use o recurso STATPLOT para verificar se o gráfico de dispersão segue um padrão logarítmico, conforme mostrado na Figura\(\PageIndex{3}\):
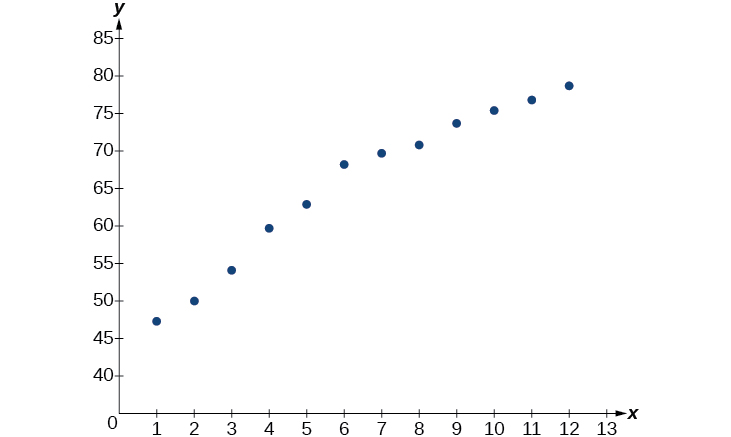
Figura\(\PageIndex{3}\)
Use o comando “lnReg” do menu STAT e depois CALC para obter o modelo logarítmico,
\(y=42.52722583+13.85752327\ln(x)\)
Em seguida, represente graficamente o modelo na mesma janela do gráfico de dispersão para verificar se ele é um bom ajuste, conforme mostrado na Figura\(\PageIndex{4}\):
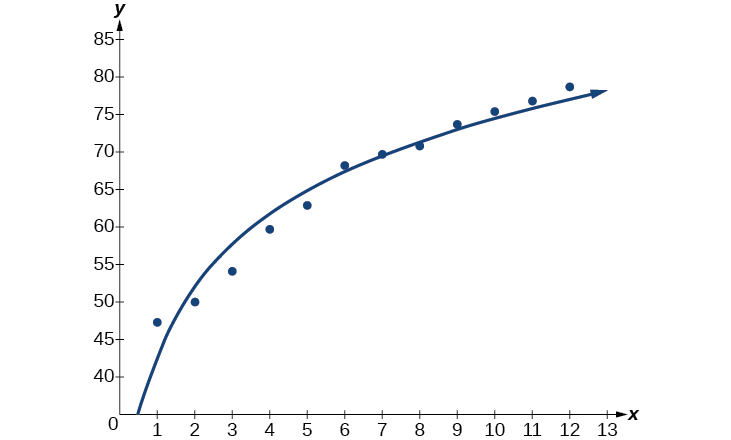
Figura\(\PageIndex{4}\)
- Para prever a expectativa de vida de um americano no ano\(2030\),\(x=14\) substitua o do modelo e resolva por\(y\):
\[\begin{align*} y&= 42.52722583+13.85752327\ln(x) \qquad \text{Use the regression model found in part } (a)\\ &= 42.52722583+13.85752327\ln(14) \qquad \text{Substitute 14 for x}\\ &\approx 79.1 \qquad \text{Round to the nearest tenth} \end{align*}\]
Se a expectativa de vida continuar aumentando nesse ritmo, a expectativa média de vida de um americano será\(79.1\) por ano\(2030\).
As vendas de um videogame lançado no ano 2000 decolaram no início, mas depois diminuíram constantemente com o passar do tempo. A tabela\(\PageIndex{4}\) mostra o número de jogos vendidos, em milhares, entre os anos de 2000 e 2010.
| Ano | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
|---|---|---|---|---|---|---|
| Número vendido (milhares) | 142 | 149 | 154 | 155 | 159 | 161 |
| Ano | 2006 | 2007 | 2008 | 2009 | 2010 | - |
| Número vendido (milhares) | 163 | 164 | 164 | 166 | 167 | - |
Vamos\(x\) representar o tempo em anos, começando com\(x=1\) o ano 2000. Vamos\(y\) representar o número de jogos vendidos em milhares.
- Use a regressão logarítmica para ajustar um modelo a esses dados.
- Se os jogos continuarem sendo vendidos nesse ritmo, quantos jogos serão vendidos em 2015? Arredonde para o milhar mais próximo.
- Responda a um
-
O modelo de regressão logarítmica que se ajusta a esses dados é\(y=141.91242949+10.45366573\ln(x)\)
- Resposta b
-
Se as vendas continuarem nesse ritmo, cerca de\(171,000\) jogos serão vendidos no ano\(2015\).
Construindo um modelo logístico a partir de dados
Assim como o crescimento exponencial e logarítmico, o crescimento logístico aumenta com o tempo. Uma das diferenças mais notáveis com os modelos de crescimento logístico é que, em um determinado ponto, o crescimento diminui constantemente e a função se aproxima de um limite superior, ou valor limite. Por causa disso, a regressão logística é melhor para modelar fenômenos em que há limites na expansão, como disponibilidade de espaço vital ou nutrientes.
Vale ressaltar que as funções logísticas, na verdade, modelam o crescimento exponencial limitado por recursos. Existem muitos exemplos desse tipo de crescimento em situações do mundo real, incluindo crescimento populacional e disseminação de doenças, rumores e até manchas no tecido. Ao realizar a análise de regressão logística, usamos o formulário mais comumente usado em utilitários gráficos:
\(y=\dfrac{c}{1+ae^{−bx}}\)
Lembre-se de que:
- \(\dfrac{c}{1+a}\)é o valor inicial do modelo.
- quando\(b>0\), o modelo aumenta rapidamente no início até atingir seu ponto de taxa máxima de crescimento,\((\dfrac{\ln(a)}{b}, \dfrac{c}{2})\). Nesse ponto, o crescimento diminui constantemente e a função se torna assintótica em relação ao limite superior\(y=c\).
- \(c\)é o valor limite, às vezes chamado de capacidade de carga, do modelo.
A regressão logística é usada para modelar situações em que o crescimento acelera rapidamente no início e depois desacelera constantemente até um limite superior. Usamos o comando “Logística” em um utilitário gráfico para ajustar uma função logística a um conjunto de pontos de dados. Isso retorna uma equação da forma
\[y=\dfrac{c}{1+ae^{−bx}}\]
Note que
- O valor inicial do modelo é\(\dfrac{c}{1+a}\).
- Os valores de saída do modelo se aproximam cada vez mais à\(y=c\) medida que o tempo aumenta.
- Use o menu STAT e EDIT para inserir dados fornecidos.
- Limpe todos os dados existentes das listas.
- Liste os valores de entrada na coluna L1.
- Liste os valores de saída na coluna L2.
- Faça um gráfico e observe um gráfico de dispersão dos dados usando o recurso STATPLOT.
- Use ZOOM [9] para ajustar os eixos para se ajustarem aos dados.
- Verifique se os dados seguem um padrão logístico.
- Encontre a equação que modela os dados.
- Selecione “Logística” no menu STAT e depois CALC.
- Use os valores retornados para\(a\)\(b\), e\(c\) para registrar o modelo,\(y=\dfrac{c}{1+ae^{−bx}}\).
- Faça um gráfico do modelo na mesma janela do gráfico de dispersão para verificar se ele é um bom ajuste para os dados.
O serviço de telefonia móvel aumentou rapidamente nos Estados Unidos desde meados da década de 1990. Hoje, quase todos os residentes têm serviço de celular. A tabela\(\PageIndex{5}\) mostra a porcentagem de americanos com serviço de celular entre os anos de 1995 e 2012.
| Ano | Americanos com serviço de celular (%) | Ano | Americanos com serviço de celular (%) |
|---|---|---|---|
| 1995 | 12,69 | 2004 | 62.852 |
| 1996 | 16,35 | 2005 | 68,63 |
| 1997 | 20,29 | 2006 | 76,64 |
| 1998 | 25,08 | 2007 | 82,47 |
| 1999 | 30,81 | 2008 | 85,68 |
| 2000 | 38,75 | 2009 | 89,14 |
| 2001 | 45,00 | 2010 | 91,86 |
| 2002 | 49,16 | 2011 | 95,28 |
| 2003 | 55.15 | 2012 | 98,17 |
- Vamos\(x\) representar o tempo em anos, começando com\(x=0\) o ano de 1995. Vamos\(y\) representar a porcentagem correspondente de residentes com serviço de celular. Use a regressão logística para ajustar um modelo a esses dados.
- Use o modelo para calcular a porcentagem de americanos com serviço de celular no ano de 2013. Arredonde para o décimo de um por cento mais próximo.
- Discuta o valor retornado para o limite superior,\(c\). O que isso diz sobre o modelo? Qual seria o valor limite se o modelo fosse exato?
Solução
- Usando o menu STAT e EDIT em um utilitário gráfico, liste os anos usando valores\(0–15\) em L1 e a porcentagem correspondente em L2. Em seguida, use o recurso STATPLOT para verificar se o gráfico de dispersão segue um padrão logístico, conforme mostrado na Figura\(\PageIndex{5}\):
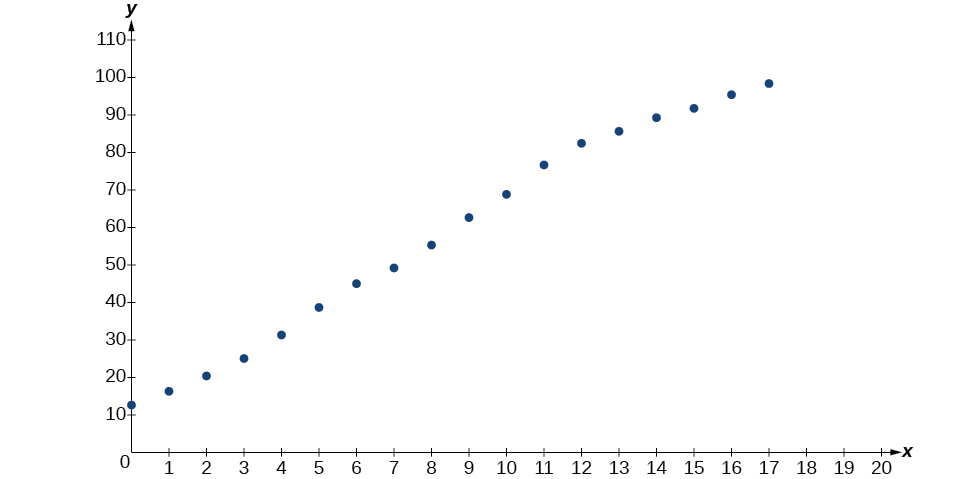
Figura\(\PageIndex{5}\)
Use o comando “Logística” do menu STAT e depois CALC para obter o modelo logístico,
\[y=105.73795261+6.88328979e^{−0.2595440013x}\]
Em seguida, faça um gráfico do modelo na mesma janela mostrada na Figura\(\PageIndex{6}\) do gráfico de dispersão para verificar se ele é um bom ajuste:
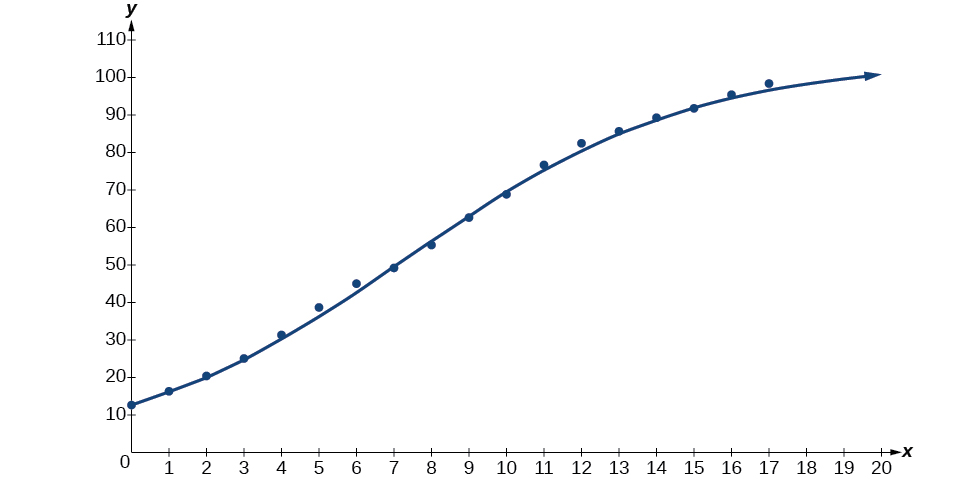
Figura\(\PageIndex{6}\)
- Para aproximar a porcentagem de americanos com serviço de celular no ano de 2013,\(x=18\) substitua o no modelo e resolva por\(y\):
\[\begin{align*} y&= \dfrac{105.7379526}{1+6.88328979e^{-0.2595440013x}} \qquad \text{Use the regression model found in part } (a)\\ &= \dfrac{105.7379526}{1+6.88328979e^{-0.2595440013(18)}} \qquad \text{Substitute 18 for x}\\ &\approx 99.3 \qquad \text{Round to the nearest tenth} \end{align*}\]
De acordo com o modelo, cerca de 98,8% dos americanos tinham serviço de celular em 2013.
- O modelo fornece um valor limite de cerca de\(105\). Isso significa que a porcentagem máxima possível de americanos com serviço de celular seria\(105%\), o que é impossível. (Como mais\(100%\) de uma população pode ter serviço de celular?) Se o modelo fosse exato, o valor limite seria\(c=100\) e as saídas do modelo ficariam muito próximas, mas nunca realmente alcançariam\(100%\). Afinal, sempre haverá alguém sem serviço de celular!
A tabela\(\PageIndex{6}\) mostra a população, em milhares, de focas no Mar de Wadden durante os anos de 1997 a 2012.
| Ano | População de focas (milhares) | Ano | População de focas (milhares) |
|---|---|---|---|
| 1997 | 3.493 | 2005 | 19.590 |
| 1998 | 5.282 | 2006 | 21.955 |
| 1999 | 6.357 | 2007 | 22.862 |
| 2000 | 9.201 | 2008 | 23.869 |
| 2001 | 11.224 | 2009 | 24.243 |
| 2002 | 12.964 | 2010 | 24,34 |
| 2003 | 16.226 | 2011 | 24.919 |
| 2004 | 18.137 | 2012 | 25.108 |
Vamos\(x\) representar o tempo em anos, começando com\(x=0\) o ano de 1997. Vamos\(y\) representar o número de selos em milhares.
- Use a regressão logística para ajustar um modelo a esses dados.
- Use o modelo para prever a população de focas para o ano de 2020.
- Para o número inteiro mais próximo, qual é o valor limite desse modelo?
- Responda a um
-
O modelo de regressão logística que se ajusta a esses dados é\(y=\dfrac{25.65665979}{1+6.113686306e^{−0.3852149008x}}\).
- Resposta b
-
Se a população continuar crescendo nesse ritmo, haverá cerca de\(25,634\) focas em 2020.
- Resposta c
-
Para o número inteiro mais próximo, a capacidade de carga é\(25,657\).
Acesse esse recurso on-line para obter instruções e práticas adicionais com modelos de função exponencial.
Visite este site para obter mais perguntas práticas do Learningpod.
Conceitos chave
- A regressão exponencial é usada para modelar situações em que o crescimento começa lentamente e depois acelera rapidamente sem limites, ou onde a decadência começa rapidamente e depois diminui para chegar cada vez mais perto de zero.
- Usamos o comando “ExpReg” em um utilitário gráfico para ajustar a função do formulário\(y=ab^x\) a um conjunto de pontos de dados. Veja o exemplo\(\PageIndex{1}\).
- A regressão logarítmica é usada para modelar situações em que o crescimento ou a decadência aceleram rapidamente no início e depois diminuem com o tempo.
- Usamos o comando “LNReg” em um utilitário gráfico para ajustar uma função do formulário\(y=a+b\ln(x)\) a um conjunto de pontos de dados. Veja o exemplo\(\PageIndex{2}\).
- A regressão logística é usada para modelar situações em que o crescimento acelera rapidamente no início e depois diminui constantemente à medida que a função se aproxima de um limite superior.
- Usamos o comando “Logística” em um utilitário gráfico para ajustar uma função do formulário\(y=\dfrac{c}{1+ae^{−bx}}\) a um conjunto de pontos de dados. Veja o exemplo\(\PageIndex{3}\).


