6.8: Modelos exponenciais e logarítmicos

objetivos de aprendizagem

• Modele o crescimento e a decadência exponenciais.
• Use a Lei do Resfriamento de Newton.
• Use modelos de crescimento logístico.
• Escolha um modelo apropriado para os dados.
• Expresse um modelo exponencial na base\(e\).

Já exploramos algumas aplicações básicas de funções exponenciais e logarítmicas. Nesta seção, exploramos algumas aplicações importantes com mais profundidade, incluindo isótopos radioativos e a Lei do Resfriamento de Newton.

Figura\(\PageIndex{1}\): Um reator de pesquisa nuclear dentro do Centro de Pesquisa Nuclear Neely, no campus do Instituto de Tecnologia da Geórgia (crédito: Instituto de Pesquisa Tecnológica da Geórgia)

Modelando crescimento e decaimento exponenciais

Em aplicações do mundo real, precisamos modelar o comportamento de uma função. Na modelagem matemática, escolhemos uma função geral familiar com propriedades que sugerem que ela modelará o fenômeno do mundo real que desejamos analisar. No caso de crescimento rápido, podemos escolher a função de crescimento exponencial:

\[y=A_0e^{kt}\]

onde\(A_0\) é igual ao valor no tempo zero,\(e\) é a constante de Euler e\(k\) é uma constante positiva que determina a taxa (porcentagem) de crescimento. Podemos usar a função de crescimento exponencial em aplicações que envolvem o tempo de duplicação, o tempo necessário para uma quantidade dobrar. Fenômenos como populações de animais selvagens, investimentos financeiros, amostras biológicas e recursos naturais podem apresentar crescimento com base em um tempo de duplicação. Em algumas aplicações, no entanto, como veremos quando discutirmos a equação logística, o modelo logístico às vezes ajusta melhor os dados do que o modelo exponencial.

Por outro lado, se uma quantidade está caindo rapidamente em direção a zero, sem nunca chegar a zero, então provavelmente devemos escolher o modelo de decaimento exponencial. Novamente, temos a forma\(y=A_0e^{kt}\) em que\(A_0\) é o valor inicial e\(e\) é a constante de Euler. Agora\(k\) é uma constante negativa que determina a taxa de decaimento. Podemos usar o modelo de decaimento exponencial quando calculamos a meia-vida, ou o tempo que uma substância leva para decair exponencialmente até a metade de sua quantidade original. Usamos meia-vida em aplicações envolvendo isótopos radioativos.

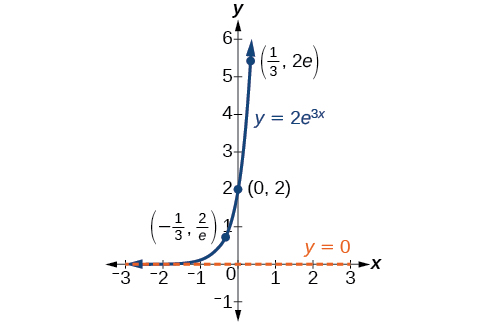
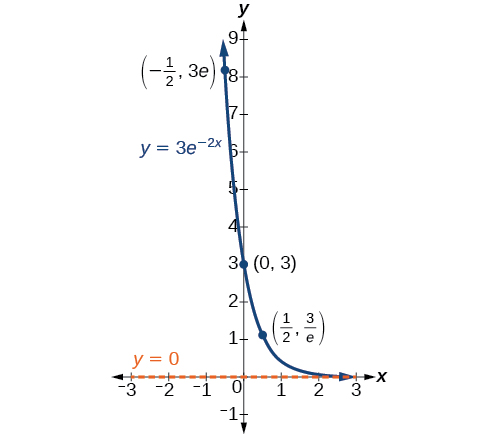
Em nossa escolha de uma função para servir como modelo matemático, geralmente usamos pontos de dados coletados por observação e medição cuidadosas para construir pontos em um gráfico e esperamos poder reconhecer a forma do gráfico. Os gráficos exponenciais de crescimento e decaimento têm uma forma distinta, como podemos ver na Figura\(\PageIndex{2}\) e na Figura\(\PageIndex{3}\). É importante lembrar que, embora partes de cada um dos dois gráficos pareçam estar no\(x\) eixo -, elas estão realmente a uma pequena distância acima do\(x\) eixo.

Figura\(\PageIndex{2}\): Um gráfico mostrando o crescimento exponencial. A equação é\(y=2e^{3x}\).

Figura\(\PageIndex{3}\): Um gráfico mostrando o decaimento exponencial. A equação é\(y=3e^{−2x}\).

O crescimento e a decadência exponenciais geralmente envolvem números muito grandes ou muito pequenos. Para descrever esses números, geralmente usamos ordens de magnitude. A ordem de magnitude é a potência de dez, quando o número é expresso em notação científica, com um dígito à esquerda do decimal. Por exemplo, a distância até a estrela mais próxima, Proxima Centauri, medida em quilômetros, é de\(40,113,497,200,000\) quilômetros. Expresso em notação científica, isso é\(4.01134972 × 1013\). Então, poderíamos descrever esse número como tendo uma ordem de magnitude\(1013\).

\(y=a_0e^{kt}\)

Uma função exponencial com a forma\(y=A_0e^{kt}\) tem as seguintes características:

• função um para um
• assíntota horizontal:\(y=0\)
• domínio:\((–\infty, \infty)\)
• alcance:\((0,\infty)\)
• \(x\)interceptar: nenhum
• \(y\)-interceptar:\((0,A_0)\)
• aumentando se\(k>0\) (veja a Figura\(\PageIndex{4}\))
• diminuindo se\(k<0\) (veja a Figura\(\PageIndex{4}\))

0 e com os pontos rotulados (1/k, (A_0) e), (0, A_0) e (-1/k, (A_0) /e). O segundo gráfico é de quando k<0 e com os pontos rotulados (-1/k, (A_0) e), (0, A_0) e (1/k, (A_0) /e)." src="https://math.libretexts.org/@api/dek.../fig_6.8.4.jpg">

Figura\(\PageIndex{4}\): Uma função exponencial modela o crescimento exponencial quando\(k>0\) e o decaimento exponencial quando\(k<0\).

Exemplo\(\PageIndex{1}\): Graphing Exponential Growth

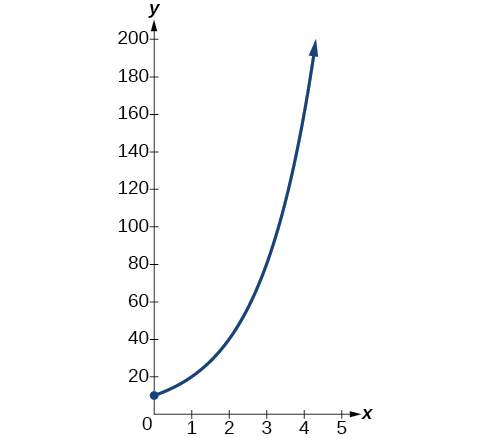
A população de bactérias dobra a cada hora. Se a cultura começou com\(10\) bactérias, represente graficamente a população em função do tempo.

Solução

Quando um valor cresce a uma porcentagem fixa por unidade de tempo, o crescimento é exponencial. Para descobrir,\(A_0\) usamos o fato de que\(A_0\) é a quantidade no tempo zero, então\(A_0=10\). Para encontrar\(k\), use o fato de que após uma hora\((t=1)\) a população dobra de\(10\) para\(20\) .A fórmula é derivada da seguinte forma

\[\begin{align*} 20&= 10e^{k\cdot 1}\\ 2&= e^k \qquad \text{Divide by 10}\\ \ln2&= k \qquad \text{Take the natural logarithm} \end{align*}\]

então\(k=\ln(2)\). Portanto, a equação que queremos representar graficamente é\(y=10e^{(\ln2)t}=10{(e^{\ln2})}^t=10·2^t\). O gráfico é mostrado na Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): O gráfico de\(y=10e^{(\ln2)t}\)

Análise

A população de bactérias após dez horas é\(10,240\). Poderíamos descrever que essa quantidade está sendo da ordem de magnitude\(10^4\). A população de bactérias após vinte horas é\(10,485,760\) da ordem de magnitude\(10^7\), então podemos dizer que a população aumentou em três ordens de magnitude em dez horas.

Meia-vida

Agora nos voltamos para a decadência exponencial. Um dos termos comuns associados à decadência exponencial, como afirmado acima, é meia-vida, o tempo que uma quantidade em decomposição exponencial leva para diminuir para a metade de sua quantidade original. Todo isótopo radioativo tem meia-vida, e o processo que descreve o decaimento exponencial de um isótopo é chamado de decaimento radioativo.

Para encontrar a meia-vida de uma função que descreve o decaimento exponencial, resolva a seguinte equação:

\(\dfrac{1}{2}A_0=A_0e^{kt}\)

Descobrimos que a meia-vida depende apenas da constante\(k\) e não da quantidade inicial\(A_0\).

A fórmula é derivada da seguinte forma:

\[\begin{align*} \dfrac{1}{2}A_0&= A_0e^{kt}\\ \dfrac{1}{2}&= e^{kt} \qquad \text{Divide by } A_0\\ \ln \left (\dfrac{1}{2} \right )&= ktv \qquad \text{Take the natural log}\\ -\ln(2)&= kt \qquad \text{Apply laws of logarithms}\\ -\ln(2)k&= t \qquad \text{Divide by k} \end{align*}\]

Uma vez que\(t\), o tempo, é positivo,\(k\) deve, como esperado, ser negativo. Isso nos dá a fórmula da meia-vida

\[t=−\dfrac{\ln(2)}{k}\]

Dada a meia-vida, encontre a taxa de decaimento.

1. Escrever\(A=A_0e^{kt}\).
2. Substitua\(A\) por\(\dfrac{1}{2}A_0\) e substitua\(t\) pela meia-vida fornecida.
3. Resolva para encontrar\(k\). \(k\)Expresse como um valor exato (não arredonde).

Nota: Também é possível encontrar a taxa de decaimento usando\(k=−\ln(2)t\).

Exemplo\(\PageIndex{2}\): Finding the Function that Describes Radioactive Decay

A meia-vida do carbono-14 é de\(5,730\) anos. Expresse a quantidade de carbono-14 restante em função do tempo,\(t\).

Solução

Essa fórmula é derivada da seguinte forma.

\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for } f(t)\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{ \left (\tfrac{\ln(0.5)}{5730} \right ) t} \qquad \text{Substitute for r in the continuous growth formula} \end{align*}\]

A função que descreve esse decaimento contínuo é\(f(t)=A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\). Observamos que o coeficiente de\(t\),\(\dfrac{\ln(0.5)}{5730}≈−1.2097×10^{−4}\) é negativo, como esperado no caso de decaimento exponencial.

Exercício\(\PageIndex{1}\)

A meia-vida do plutônio-244 é de\(80,000,000\) anos. A função Find fornece a quantidade de carbono-14 restante em função do tempo, medida em anos.

Resposta

\(f(t)=A_0e^{−0.0000000087t}\)

Datação por radiocarbono

A fórmula do decaimento radioativo é importante na datação por radiocarbono, que é usada para calcular a data aproximada em que uma planta ou animal morreu. A datação por radiocarbono foi descoberta em 1949 por Willard Libby, que ganhou o Prêmio Nobel por sua descoberta. Ele compara a diferença entre a proporção de dois isótopos de carbono em um artefato orgânico ou fóssil com a proporção desses dois isótopos no ar. Acredita-se que seja exato quanto ao\(1\%\) erro de plantas ou animais que morreram nos últimos\(60,000\) anos.

O carbono-14 é um isótopo radioativo de carbono que tem meia-vida de\(5,730\) anos. Ela ocorre em pequenas quantidades no dióxido de carbono no ar que respiramos. A maior parte do carbono na Terra é carbono-12, que tem um peso atômico de\(12\) e não é radioativo. Os cientistas determinaram a proporção de carbono-14 para carbono-12 no ar nos últimos\(60,000\) anos, usando anéis de árvores e outras amostras orgânicas de datas conhecidas, embora a proporção tenha mudado ligeiramente ao longo dos séculos.

Enquanto uma planta ou animal estiver vivo, a proporção dos dois isótopos de carbono em seu corpo é próxima à proporção na atmosfera. Quando morre, o carbono-14 em seu corpo se decompõe e não é substituído. Ao comparar a proporção de carbono-14 para carbono-12 em uma amostra em decomposição com a proporção conhecida na atmosfera, a data em que a planta ou animal morreu pode ser aproximada.

Como a meia-vida do carbono-14 é de\(5,730\) anos, a fórmula para a quantidade de carbono-14 restante após\(t\) anos é

\(A≈A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\)

onde

• \(A\)é a quantidade de carbono 14 restante
• \(A_0\)é a quantidade de carbono-14 quando a planta ou animal começou a se decompor.

Essa fórmula é derivada da seguinte forma:

\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for f(t)}\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t} \qquad \text{Substitute for r in the continuous growth formula}\\ \end{align*}\]

Para descobrir a idade de um objeto, resolvemos essa equação para\(t\):

\(t=\dfrac{\ln \left (\dfrac{A}{A_0} \right )}{−0.000121}\)

Por necessidade, negligenciamos aqui os muitos detalhes que um cientista leva em consideração ao fazer a datação por carbono 14, e olhamos apenas para a fórmula básica. A proporção de carbono-14 para carbono-12 na atmosfera é de aproximadamente\(0.0000000001%\). \(r\)Seja a proporção de carbono-14 para carbono-12 no artefato orgânico ou fóssil a ser datado, determinado por um método chamado cintilação líquida. A partir da equação,\(A≈A_0e^{−0.000121t}\) sabemos que a razão entre a porcentagem de carbono-14 no objeto que estamos datando e a porcentagem de carbono-14 na atmosfera é\(r=\dfrac{A}{A_0}≈e^{−0.000121t}\). Resolvemos essa equação para\(t\), para obter

\(t=\dfrac{\ln(r)}{−0.000121}\)

Dada a porcentagem de carbono-14 em um objeto, determine sua idade.

1. Expresse a porcentagem dada de carbono-14 como um decimal equivalente,\(k\).
2. Substitua por\(k\) na equação\(t=\dfrac{\ln(r)}{−0.000121}\) e resolva a idade,\(t\).

Exemplo\(\PageIndex{3}\): Finding the Age of a Bone

Foi encontrado um fragmento ósseo que contém\(20\%\) seu carbono-14 original. Até o ano mais próximo, quantos anos tem o osso?

Solução

Substituímos\(20\%=0.20\) por\(k\) na equação e resolvemos por\(t\):

\[\begin{align*} t&= \dfrac{\ln(r)}{-0.000121} \qquad \text{Use the general form of the equation}\\ &= \dfrac{\ln(0.20)}{-0.000121} \qquad \text{Substitute for r}\\ &\approx 13301 \qquad \text{Round to the nearest year} \end{align*}\]

O fragmento ósseo tem cerca de\(13,301\) anos.

Análise

Os instrumentos que medem a porcentagem de carbono-14 são extremamente sensíveis e, como mencionamos acima, um cientista precisará trabalhar muito mais do que nós para ficar satisfeito. Mesmo assim, a datação por carbono só tem precisão de cerca de\(1\%\), então essa idade deve ser dada como\(13,301\) anos\(\pm 1\%\) ou\(13,301\) anos\(\pm 133\) anos.

Exercício\(\PageIndex{2}\)

O césio-137 tem uma meia-vida de cerca de\(30\) anos. Se começarmos com\(200\) mg de césio-137, levará mais ou menos de\(230\) anos até restar apenas um\(1\) miligrama?

Resposta

menos de\(230\) anos,\(229.3157\) para ser exato

Calculando o tempo de duplicação

Para quantidades em decomposição, determinamos quanto tempo levou para metade de uma substância se decompor. Para quantidades crescentes, talvez queiramos descobrir quanto tempo leva para uma quantidade dobrar. Como mencionamos acima, o tempo necessário para uma quantidade dobrar é chamado de tempo de duplicação.

Dada a equação básica do crescimento exponencial\(A=A_0e^{kt}\), o tempo de duplicação pode ser encontrado resolvendo quando a quantidade original dobrou, ou seja, resolvendo\(2A_0=A_0e^{kt}\).

A fórmula é derivada da seguinte forma:

\[\begin{align*} 2A_0&= A_0e^{kt}\\ 2&= e^{kt} \qquad \text{Divide by } A_0\\ \ln2&= kt \qquad \text{Take the natural logarithm}\\ t& =\dfrac{\ln2}{k} \qquad \text{Divide by the coefficient of t} \end{align*}\]

Assim, o tempo de duplicação é

\[t=\dfrac{\ln2}{k}\]

Exemplo\(\PageIndex{4}\): Finding a Function That Describes Exponential Growth

De acordo com a Lei de Moore, o tempo de duplicação do número de transistores que podem ser colocados em um chip de computador é de aproximadamente dois anos. Dê uma função que descreva esse comportamento.

Solução

A fórmula é derivada da seguinte forma:

\[\begin{align*} t&= \dfrac{\ln2}{k} \qquad \text{The doubling time formula}\\ 2&= \dfrac{\ln2}{k} \qquad \text{Use a doubling time of two years}\\ k&= \dfrac{\ln2}{2} \qquad \text{Multiply by k and divide by 2}\\ A&= A_0e^{\tfrac{\ln2}{2}t} \qquad \text{Substitute k into the continuous growth formula} \end{align*}\]

A função é\(A=A_0e^{\dfrac{\ln2}{2}t}\).

Exercício\(\PageIndex{3}\)

Dados recentes sugerem que, a partir de 2013, a taxa de crescimento prevista pela Lei de Moore não se mantém mais. O crescimento diminuiu para um período de duplicação de aproximadamente três anos. Encontre a nova função que leva em consideração esse tempo de duplicação mais longo.

Resposta

\(f(t)=A_0e^{\tfrac{\ln2}{3}t}\)

Usando a Lei de Refrigeração de Newton

O decaimento exponencial também pode ser aplicado à temperatura. Quando um objeto quente é deixado no ar circundante que está em uma temperatura mais baixa, a temperatura do objeto diminui exponencialmente, nivelando-se à medida que se aproxima da temperatura do ar ambiente. Em um gráfico da função de temperatura, o nivelamento corresponderá a uma assíntota horizontal à temperatura do ar circundante. A menos que a temperatura ambiente seja zero, isso corresponderá a uma mudança vertical da função genérica de decaimento exponencial. Essa tradução leva à Lei do Resfriamento de Newton, a fórmula científica da temperatura em função do tempo, quando a temperatura de um objeto é igualada à temperatura ambiente.

\(T(t)=ae^{kt}+T_s\)

Essa fórmula é derivada da seguinte forma:

\[\begin{align*} T(t)&= Ab^{ct}+T_s\\ T(t)&= Ae^{\ln(b^{ct})}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{ct\ln b}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{kt}+T_s \qquad \text{Rename the constant c } ln b \text{, calling it } k\\ \end{align*}\]

LEI DO RESFRIAMENTO DE NEWTON

A temperatura de um objeto,\(T\), no ar circundante com a temperatura, se\(T_s\) comportará de acordo com a fórmula

\[T(t)=Ae^{kt}+T_s\]

onde

• \(t\)está na hora
• \(A\)é a diferença entre a temperatura inicial do objeto e o ambiente
• \(k\)é uma constante, a taxa contínua de resfriamento do objeto

Dado um conjunto de condições, aplique a Lei de Resfriamento de Newton.

1. Defina\(T_s\) igual à\(y\) coordenada -da assíntota horizontal (geralmente a temperatura ambiente).
2. Substitua os valores fornecidos na fórmula de crescimento contínuo\(T(t)=Ae^{kt}+T_s\) para encontrar os parâmetros\(A\)\(k\) e.
3. Substitua no tempo desejado para encontrar a temperatura ou a temperatura desejada para encontrar a hora.

Exemplo\(\PageIndex{5}\): Using Newton’s Law of Cooling

Um cheesecake é retirado do forno com uma temperatura interna ideal de\(165°F\) e colocado na\(35°F\) geladeira. Depois de\(10\) minutos, o cheesecake esfriou até\(150°F\). Se precisarmos esperar até que o cheesecake esfrie\(70°F\) antes de comê-lo, quanto tempo teremos que esperar?

Solução

Como a temperatura do ar ambiente na geladeira é de\(35\) graus, a temperatura do cheesecake diminuirá exponencialmente em direção a\(35\), seguindo a equação

\(T(t)=Ae^{kt}+35\)

Sabemos que a temperatura inicial era\(165\), então\(T(0)=165\).

\[\begin{align*} 165&= Ae^{k0}+35 \qquad \text{Substitute } (0,165)\\ A&= 130 \qquad \text{Solve for A} \end{align*}\]

Recebemos outro ponto de dados\(T(10)=150\), que podemos usar para resolver\(k\).

\[\begin{align*} 150&= 130e^{k10}+35 \qquad \text{Substitute } (10, 150)\\ 115&= 130e^{k10} \qquad \text{Subtract 35}\\ \dfrac{115}{130}&= e^{10k} \qquad \text{Divide by 130}\\ \ln\left (\dfrac{115}{130} \right )&= 10k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln \left (\dfrac{115}{130} \right )}{10}\\ &= -0.0123 \qquad \text{Divide by the coefficient of k} \end{align*}\]

Isso nos dá a equação para o resfriamento do cheesecake:\(T(t)=130e^{–0.0123t}+35\).

Agora podemos resolver o tempo necessário para que a temperatura esfrie em\(70\) graus.

\[\begin{align*} 70&= 130e^{-0.0123t}+35 \qquad \text{Substitute in 70 for } T(t)\\ 35&= 130e^{-0.0123t} \qquad \text{Subtract 35}\\ \dfrac{35}{130}&= e^{-0.0123t} \qquad \text{Divide by 130}\\ \ln \left (\dfrac{35}{130} \right )&= -0.0123t \qquad \text{Take the natural log of both sides}\\ t&= \dfrac{\ln \left (\dfrac{35}{130} \right )}{-0.0123}\\ &\approx 106.68 \qquad \text{Divide by the coefficient of t} \end{align*}\]

Levará cerca de\(107\) minutos, ou uma hora e\(47\) minutos, para que o cheesecake esfrie\(70°F\).

Exercício\(\PageIndex{4}\)

Uma jarra de água a\(40\) graus Fahrenheit é colocada em uma sala\(70\) de graduação. Uma hora depois, a temperatura subiu para\(45\) graus. Quanto tempo vai demorar para que a temperatura suba para\(60\) graus?

Resposta

\(6.026\)horas

Usando modelos de crescimento logístico

O crescimento exponencial não pode continuar para sempre. Os modelos exponenciais, embora possam ser úteis no curto prazo, tendem a se desfazer quanto mais tempo continuam. Considere uma aspirante a escritora que escreve uma única linha no primeiro dia e planeja dobrar o número de linhas que ela escreve todos os dias durante um mês. Até o final do mês, ela deve escrever mais de um\(17\) bilhão de linhas, ou meio bilhão de páginas. É impraticável, senão impossível, que alguém escreva tanto em tão pouco tempo. Eventualmente, um modelo exponencial deve começar a se aproximar de algum valor limitante e, em seguida, o crescimento é forçado a desacelerar. Por esse motivo, geralmente é melhor usar um modelo com um limite superior em vez de um modelo de crescimento exponencial, embora o modelo de crescimento exponencial ainda seja útil em um curto prazo, antes de se aproximar do valor limite.

O modelo de crescimento logístico é aproximadamente exponencial no início, mas tem uma taxa de crescimento reduzida à medida que a produção se aproxima do limite superior do modelo, chamado de capacidade de carga. Para constantes\(a\),, e\(b\)\(c\), o crescimento logístico de uma população ao longo do tempo\(x\) é representado pelo modelo

\(f(x)=\dfrac{c}{1+ae^{−bx}}\)

O gráfico na Figura\(\PageIndex{6}\) mostra como a taxa de crescimento muda ao longo do tempo. O gráfico aumenta da esquerda para a direita, mas a taxa de crescimento só aumenta até atingir seu ponto de taxa máxima de crescimento, momento em que a taxa de aumento diminui.

Figura\(\PageIndex{6}\)

CRESCIMENTO LOGÍSTICO

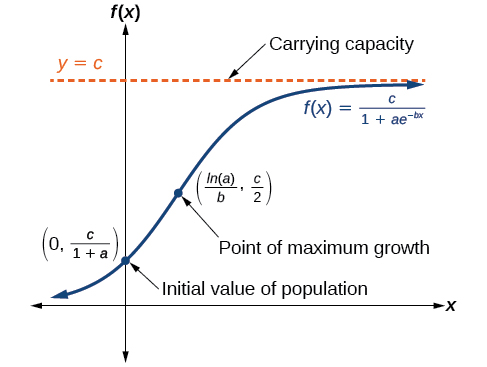
O modelo de crescimento logístico é

\[f(x)=\dfrac{c}{1+ae^{−bx}}\]

onde

• \(\dfrac{c}{1+a}\)é o valor inicial
• \(c\)é a capacidade de carga ou o valor limite
• \(b\)é uma constante determinada pela taxa de crescimento.

Exemplo\(\PageIndex{6}\): Using the Logistic-Growth Model

Uma epidemia de gripe se espalha rapidamente pela população, a uma taxa que depende de dois fatores: quanto mais pessoas estão gripadas, mais rapidamente ela se espalha, e também quanto mais pessoas não infectadas existem, mais rapidamente ela se espalha. Esses dois fatores fazem do modelo logístico um bom modelo para estudar a propagação de doenças transmissíveis. E, claramente, há um valor máximo para o número de pessoas infectadas: toda a população.

Por exemplo, às vezes\(t=0\) há uma pessoa em uma comunidade de\(1,000\) pessoas que está gripada. Então, nessa comunidade, a maioria das\(1,000\) pessoas pode ter gripe. Os pesquisadores descobriram que, para essa cepa específica da gripe, a constante de crescimento logístico é\(b=0.6030\). Estime o número de pessoas nessa comunidade que terão tido essa gripe após dez dias. Preveja quantas pessoas nessa comunidade terão tido essa gripe após um longo período de tempo.

Solução

Substituímos os dados fornecidos no modelo de crescimento logístico

\(f(x)=\dfrac{c}{1+ae^{−bx}}\)

Como a maioria das\(1,000\) pessoas, toda a população da comunidade, pode pegar gripe, sabemos que o valor limite é\(c=1000\). Para descobrir\(a\), usamos a fórmula de que\(t=0\) é o número de casos de cada vez\(\dfrac{c}{1+a}=1\), da qual se segue\(a=999\). Esse modelo prevê que, após dez dias, o número de pessoas que tiveram gripe é\(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}≈293.8\). Como o número real deve ser um número inteiro (uma pessoa está gripada ou não), arredondamos\(294\). A longo prazo, o número de pessoas que contrairão a gripe é o valor limite,\(c=1000\).

Análise

Lembre-se de que, como estamos lidando com um vírus, não podemos prever com certeza o número de pessoas infectadas. O modelo se aproxima apenas do número de pessoas infectadas e não nos fornecerá valores exatos ou reais.

O gráfico na Figura\(\PageIndex{7}\) fornece uma boa imagem de como esse modelo ajusta os dados.

Figura\(\PageIndex{7}\): O gráfico de\(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}\)

Exercício\(\PageIndex{5}\)

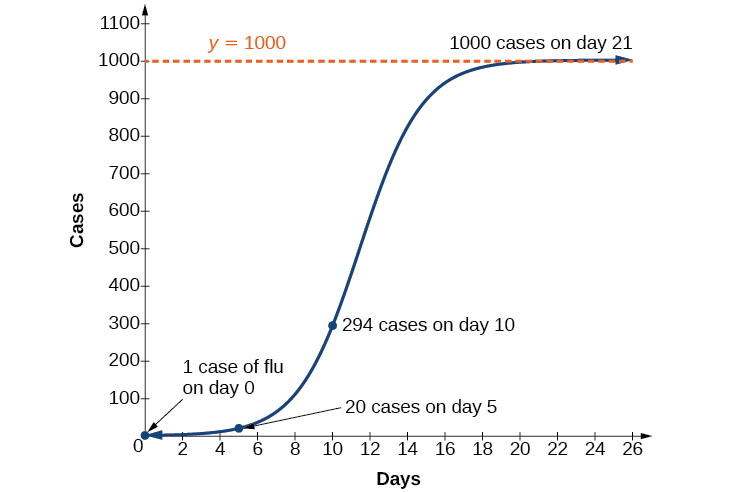
Usando o modelo no exemplo acima, estime o número de casos de gripe no dia\(15\).

Resposta

\(895\)casos no dia\(15\)

Escolhendo um modelo apropriado para dados

Agora que discutimos vários modelos matemáticos, precisamos aprender como escolher o modelo apropriado para os dados brutos que temos. Muitos fatores influenciam a escolha de um modelo matemático, entre os quais a experiência, as leis científicas e os padrões nos próprios dados. Nem todos os dados podem ser descritos por funções elementares. Às vezes, é escolhida uma função que aproxima os dados em um determinado intervalo. Por exemplo, suponha que foram coletados dados sobre o número de casas compradas nos Estados Unidos dos anos 1960 a 2013. Depois de traçar esses dados em um gráfico de dispersão, notamos que a forma dos dados dos anos 2000 a 2013 segue uma curva logarítmica. Poderíamos restringir o intervalo de 2000 a 2010, aplicar a análise de regressão usando um modelo logarítmico e usá-lo para prever o número de compradores de imóveis para o ano de 2015.

Três tipos de funções que geralmente são úteis em modelos matemáticos são funções lineares, funções exponenciais e funções logarítmicas. Se os dados estiverem em uma linha reta ou parecerem estar aproximadamente ao longo de uma linha reta, um modelo linear pode ser o melhor. Se os dados não forem lineares, geralmente consideramos um modelo exponencial ou logarítmico, embora outros modelos, como modelos quadráticos, também possam ser considerados.

Ao escolher entre um modelo exponencial e um modelo logarítmico, observamos a forma como os dados se curvam. Isso é chamado de concavidade. Se traçarmos uma linha entre dois pontos de dados e todos (ou a maioria) dos dados entre esses dois pontos estiverem acima dessa linha, dizemos que a curva é côncava para baixo. Podemos pensar nisso como uma tigela que se inclina para baixo e, portanto, não pode reter água. Se todos (ou a maioria) dos dados entre esses dois pontos estiverem abaixo da linha, dizemos que a curva é côncava para cima. Nesse caso, podemos pensar em uma tigela que se inclina para cima e, portanto, pode reter água. Uma curva exponencial, seja subindo ou descendo, representando crescimento ou decaimento, é sempre côncava para cima, longe de sua assíntota horizontal. Uma curva logarítmica é sempre côncava longe de sua assíntota vertical. No caso de dados positivos, que é o caso mais comum, uma curva exponencial é sempre côncava para cima e uma curva logarítmica sempre côncava para baixo.

Uma curva logística muda a concavidade. Ele começa côncavo para cima e depois muda para côncavo para baixo além de um certo ponto, chamado de ponto de inflexão.

Depois de usar o gráfico para nos ajudar a escolher um tipo de função para usar como modelo, substituímos os pontos e resolvemos para encontrar os parâmetros. Reduzimos o erro de arredondamento escolhendo os pontos o mais distantes possível.

Exemplo\(\PageIndex{7}\): Choosing a Mathematical Model

Um modelo linear, exponencial, logarítmico ou logístico se ajusta melhor aos valores listados na Tabela\(\PageIndex{1}\)? Encontre o modelo e use um gráfico para verificar sua escolha.

Tabela\(\PageIndex{1}\)

\(x\)	1	2	3	4	5	6	7	8	9
\(y\)	0	1.386	2.197	2.773	3.219	3.584	3.892	4.159	4.394

Solução

Primeiro, plote os dados em um gráfico como na Figura\(\PageIndex{8}\). Para fins de representação gráfica, arredonde os dados para dois dígitos significativos.

Figura\(\PageIndex{8}\)

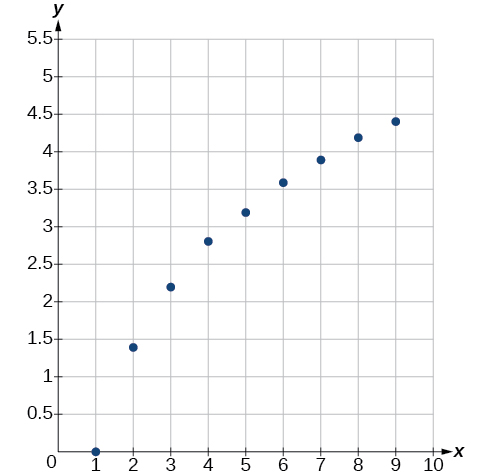
Claramente, os pontos não estão em uma linha reta, então rejeitamos um modelo linear. Se traçarmos uma linha entre quaisquer dois pontos, a maioria ou todos os pontos entre esses dois pontos estão acima da linha, então o gráfico é côncavo para baixo, sugerindo um modelo logarítmico. Nós podemos tentar\(y=a\ln(bx)\). Conectando o primeiro ponto,\((1,0)\), dá\(0=a\ln b\). Rejeitamos o caso de que\(a=0\) (se fosse, todas as saídas seriam\(0\)), então sabemos\(\ln(b)=0\). Assim\(b=1\)\(y=a\ln(x)\) e. Em seguida, podemos usar o ponto\((9,4.394)\) para resolver\(a\):

\[\begin{align*} y&= a\ln(x)\\ 4.394&= a\ln(9)\\ a&= \dfrac{4.394}{\ln(9)} \end{align*}\]

Porque\(a=\dfrac{4.394}{\ln(9)}≈2\), um modelo apropriado para os dados é\(y=2\ln(x)\).

Para verificar a precisão do modelo, representamos graficamente a função junto com os pontos fornecidos, como na Figura\(\PageIndex{9}\).

Figura\(\PageIndex{9}\): O gráfico de\(y=2\ln x\).

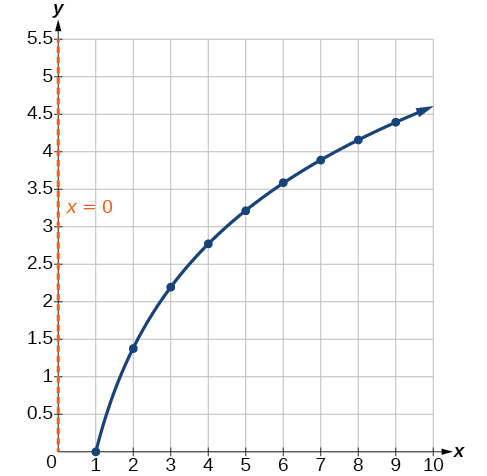
Podemos concluir que o modelo é uma boa opção para os dados.

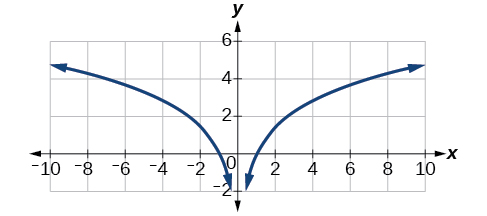
Compare\(\PageIndex{9}\) a figura com o gráfico\(y=\ln(x^2)\) mostrado na Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): O gráfico de\(y=\ln(x^2)\)

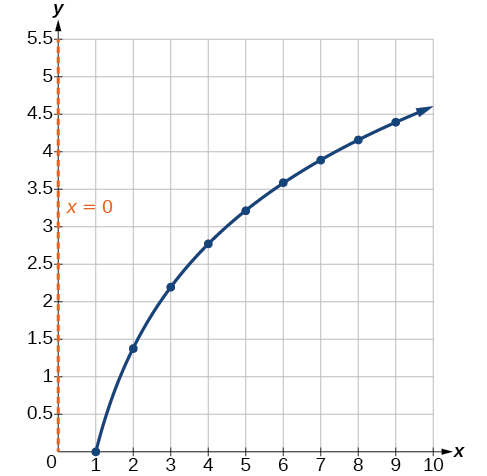
Os gráficos parecem ser idênticos quando\(x>0\). Uma verificação rápida confirma essa conclusão:\(y=\ln(x^2)=2\ln(x)\) para\(x>0\).

No entanto, se\(x<0\), o gráfico de\(y=\ln(x^2)\) inclui uma ramificação “extra”, conforme mostrado na Figura\(\PageIndex{11}\). Isso ocorre porque, embora\(y=2\ln(x)\) não possa ter valores negativos no domínio (pois esses valores forçariam o argumento a ser negativo), a função\(y=\ln(x^2)\) pode ter valores de domínio negativos.

Figura\(\PageIndex{11}\)

Exercício\(\PageIndex{6}\)

Um modelo linear, exponencial ou logarítmico se ajusta melhor aos dados na Tabela\(\PageIndex{2}\)? Encontre o modelo.

Tabela\(\PageIndex{2}\)

\(x\)	1	2	3	4	5	6	7	8	9
\(y\)	3.297	5.437	8.963	14.778	24.365	40.172	66.231	109.196	180.034

Resposta

Exponencial\(y=2e^{0.5x}\).

Expressando um modelo exponencial em base\(e\)

Embora potências e logaritmos de qualquer base possam ser usados na modelagem, as duas bases mais comuns são\(10\)\(e\) e. Em ciências e matemática, a base geralmente\(e\) é preferida. Podemos usar as leis dos expoentes e as leis dos logaritmos para mudar qualquer base para base\(e\).

Dado um modelo com o formulário\(y=ab^x\), change it to the form \(y=A_0e^{kx}\).

1. Reescreva\(y=ab^x\) como\(y=ae^{\ln(b^x)}\).
2. Use a regra de potência dos logaritmos para reescrever\(y\) como\(y=ae^{x\ln(b)}=ae^{\ln{(b)}^x}\).
3. Observe isso\(a=A_0\) e\(k=\ln(b)\) na equação\(y=A_0e^{kx}\).

Exemplo\(\PageIndex{8}\): Changing to base \(e\)

Altere a função\(y=2.5{(3.1)}^x\) para que essa mesma função seja escrita no formulário\(y=A_0e^{kx}\).

Solução

A fórmula é derivada da seguinte forma:

\[\begin{align*} y&= 2.5{(3.1)}^x\\ &= 2.5e^{\ln({3.1}^x)} \qquad \text{Insert exponential and its inverse}\\ &= 2.5e^{x\ln3.1} \qquad \text{Laws of logs}\\ &= 2.5e^{(\ln3.1)x} \qquad \text{Commutative law of multiplication} \end{align*}\]

Exercício\(\PageIndex{7}\)

Mude a função\(y=3{(0.5)}^x\) para uma que tenha\(e\) como base.

Resposta

\(y=3e^{(\ln0.5)x}\)

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com modelos exponenciais e logarítmicos.

• Aplicação de logaritmo — pH
• Modelo exponencial — Idade usando meia-vida
• Lei do Resfriamento de Newton
• Crescimento exponencial devido ao tempo de duplicação
• Crescimento exponencial - Encontre a quantidade inicial com o tempo de duplicação

Equações-chave

Fórmula de meia-vida	E se\(A=A_0e^{kt}\)\(k<0\), a meia-vida é\(t=−\dfrac{\ln(2)}{k}\).
Datação por carbono 14	\(t=\dfrac{\ln(\dfrac{A}{A_0})}{−0.000121}\). \(A_0\)\(A\)é a quantidade de carbono-14 quando a planta ou animal morreu \(t\) é a quantidade de carbono-14 restante hoje é a idade do fóssil em anos
Fórmula de tempo de duplicação	Se\(A=A_0e^{kt}\),\(k>0\), o tempo de duplicação é\(t=\dfrac{\ln2}{k}\)
Lei do Resfriamento de Newton	\(T(t)=Ae^{kt}+T_s\), onde\(T_s\) está a temperatura ambiente,\(A=T(0)−T_s\), e\(k\) é a taxa contínua de resfriamento.

Conceitos-chave

• A função exponencial básica é\(f(x)=ab^x\). Se\(b>1\), temos crescimento exponencial; se\(0<b<1\), temos decaimento exponencial.
• Também podemos escrever essa fórmula em termos de crescimento contínuo\(A=A_0e^{kx}\), pois, onde\(A_0\) está o valor inicial. Se\(A_0\) for positivo, então temos crescimento exponencial quando\(k>0\) e declínio exponencial quando\(k<0\). Veja o exemplo\(\PageIndex{1}\).
• Em geral, resolvemos problemas envolvendo crescimento ou decaimento exponencial em duas etapas. Primeiro, configuramos um modelo e usamos o modelo para encontrar os parâmetros. Em seguida, usamos a fórmula com esses parâmetros para prever o crescimento e a decadência. Veja o exemplo\(\PageIndex{2}\).
• Podemos encontrar a idade,\(t\), de um artefato orgânico medindo a quantidade\(k\),, do carbono-14 restante no artefato e usando a fórmula\(t=\dfrac{\ln(k)}{−0.000121}\) para resolver\(t\). Veja o exemplo\(\PageIndex{3}\).
• Dado o tempo de duplicação ou intervalo de uma substância, podemos encontrar uma função que represente seu crescimento ou decaimento exponencial. Veja o exemplo\(\PageIndex{4}\).
• Podemos usar a Lei do Resfriamento de Newton para descobrir quanto tempo um objeto resfriado levará para atingir a temperatura desejada ou para descobrir qual temperatura um objeto estará após um determinado tempo. Veja o exemplo\(\PageIndex{5}\).
• Podemos usar funções de crescimento logístico para modelar situações do mundo real em que a taxa de crescimento muda com o tempo, como crescimento populacional, disseminação de doenças e disseminação de boatos. Veja o exemplo\(\PageIndex{6}\).
• Podemos usar dados do mundo real coletados ao longo do tempo para observar tendências. O conhecimento de gráficos lineares, exponenciais, logarítmicos e logísticos nos ajuda a desenvolver modelos que melhor se ajustam aos nossos dados. Veja o exemplo\(\PageIndex{7}\).
• Qualquer função exponencial com a forma\(y=abx\) pode ser reescrita como uma função exponencial equivalente com a forma\(y=A_0e^{kx}\) onde\(k=\ln b\). Veja o exemplo\(\PageIndex{8}\).