1.5: Polinômios

Last updated
Save as PDF

Page ID: 189312

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Nesta seção, os alunos irão:

Identifique o grau e o coeficiente principal dos polinômios.
Adicione e subtraia polinômios.
Multiplique polinômios.
Use FOIL para multiplicar binômios.
Execute operações com polinomia
ls de várias variáveis.

Earl está construindo uma casinha de cachorro, cuja frente tem a forma de um quadrado coberto por um triângulo. Haverá uma porta retangular pela qual o cachorro poderá entrar e sair da casa. Earl quer encontrar a área da frente da casinha para poder comprar a quantidade correta de tinta. Usando as medidas da frente da casa, mostradas na Figura$\PageIndex{1}$, podemos criar uma expressão que combina vários termos variáveis, o que nos permite resolver esse problema e outros semelhantes.

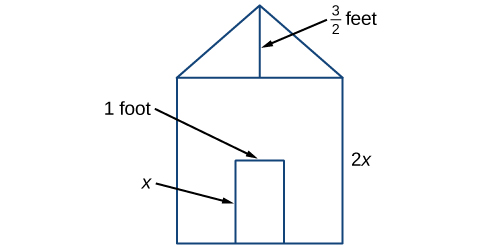
Esboço de uma casa formada por um quadrado e um triângulo com base no topo do quadrado. Um retângulo é colocado na parte inferior central do quadrado para marcar uma entrada. A altura da porta é identificada como: x e a largura da porta é rotulada: 1 pé. O lado do quadrado é rotulado: 2x. A altura do triângulo é identificada como: 3/2 pés. — Figura$\PageIndex{1}$

Primeiro, encontre a área do quadrado em pés quadrados.

\[\begin{align*} A &= s^2\\ &= {(2x)}^2\\ &= 4x^2 \end{align*}\]

Em seguida, encontre a área do triângulo em pés quadrados.

\[\begin{align*} A &= \dfrac{1}{2}bh\\ &= \dfrac{1}{2}(2x)\left (\dfrac{3}{2} \right )\\ &= \dfrac{3}{2}x \end{align*}\]

Em seguida, encontre a área da porta retangular em pés quadrados.

\[\begin{align*} A &= lw\\ &= x\times1\\ &= x \end{align*}\]

A área da frente da casinha de cachorro pode ser encontrada adicionando as áreas do quadrado e do triângulo e, em seguida, subtraindo a área do retângulo. Quando fazemos isso, obtemos

$4x^2+\dfrac{3}{2}x-x$$ft^2$

$4x^2+\dfrac{1}{2}x$$ft^2$

Nesta seção, examinaremos expressões como essa, que combinam vários termos variáveis.

Identificando o grau e o coeficiente principal de polinômios

A fórmula que acabamos de encontrar é um exemplo de um polinômio, que é uma soma ou diferença de termos, cada um consistindo em uma variável elevada a uma potência inteira não negativa. Um número multiplicado por uma variável elevada a um expoente, como$384\pi$, é conhecido como coeficiente. Os coeficientes podem ser positivos, negativos ou zero e podem ser números inteiros, decimais ou frações. Cada produto$a_ix^i$, como$384\pi w$, é um termo de um polinômio. Se um termo não contém uma variável, ele é chamado de constante.

Um polinômio contendo apenas um termo, como$5x^4$, é chamado de monômio. Um polinômio contendo dois termos, como$2x−9$, é chamado de binômio. Um polinômio contendo três termos, como$−3x^2+8x−7$, é chamado de trinômio.

Podemos encontrar o grau de um polinômio identificando a maior potência da variável que ocorre no polinômio. O termo com o grau mais alto é chamado de termo principal porque geralmente é escrito primeiro. O coeficiente do termo principal é chamado de coeficiente principal. Quando um polinômio é escrito de forma que as potências sejam decrescentes, dizemos que ele está na forma padrão.

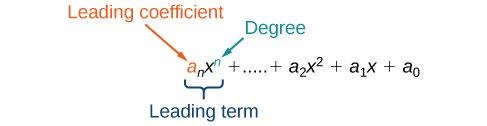
$Uma leitura polinomial: um sub n vezes x elevado à enésima potência mais e assim por diante mais um sub 2 vezes x ao quadrado mais um sub um vezes x mais um abaixo de zero é mostrado. O a no termo a sub n é rotulado como: coeficiente inicial. O n no termo x elevado à enésima potência é rotulado como: grau. Finalmente, todo o termo é rotulado como: Termo principal.$

Polinômios

Um polinômio é uma expressão que pode ser escrita na forma

\[a_nx^n+...+a_2x^2+a_1x+a_0\]

Cada número real ai é chamado de coeficiente. O número$a_0$ que não é multiplicado por uma variável é chamado de constante. Cada produto$a_ix^i$ é um termo de um polinômio. A maior potência da variável que ocorre no polinômio é chamada de grau de um polinômio. O termo principal é o termo com maior potência e seu coeficiente é chamado de coeficiente principal.

Como: Dada uma expressão polinomial, identifique o grau e o coeficiente principal.

Encontre a maior potência de x para determinar o grau.
Identifique o termo que contém a maior potência de x para encontrar o termo principal.
Identifique o coeficiente do termo principal.

Exemplo$\PageIndex{1}$: Identifying the Degree and Leading Coefficient of a Polynomial

Para os seguintes polinômios, identifique o grau, o termo principal e o coeficiente principal.

$3+2x^2−4x^3$
$5t^5−2t^3+7t$
$6p−p^3−2$

Solução

A maior potência de$x$ é$3$, então o grau é$3$. O termo principal é o termo que contém esse grau,$−4x^3$. O coeficiente principal é o coeficiente desse termo,$−4$.
A maior potência de$t$ é$5$, então o grau é$5$. O termo principal é o termo que contém esse grau,$5t^5$. O coeficiente principal é o coeficiente desse termo,$5$.
A maior potência de$p$ é$3$, então o grau é$3$. O termo principal é o termo que contém esse grau$−p^3$,, O coeficiente principal é o coeficiente desse termo, −1.

Exercício$\PageIndex{1}$

Identifique o grau, o termo principal e o coeficiente principal do polinômio$4x^2−x^6+2x−6$.

Resposta: O grau é$6$, o termo principal é$−x^6$ e o coeficiente principal é$−1$.

Adicionando e subtraindo polinômios

Podemos somar e subtrair polinômios combinando termos semelhantes, que são termos que contêm as mesmas variáveis elevadas aos mesmos expoentes. Por exemplo,$5x^2$ e$−2x^2$ são como termos e podem ser adicionados para obter$3x^2$, mas$3x$ não$3x^2$ são termos semelhantes e, portanto, não podem ser adicionados.

Como: Dados vários polinômios, adicione ou subtraia para simplificar as expressões.

Combine termos semelhantes.
Simplifique e escreva em formato padrão.

Exemplo$\PageIndex{2}$: Adding Polynomials

Encontre a soma.

$(12x^2+9x−21)+(4x^3+8x^2−5x+20)$

Solução

\[\begin{align*} &4x^3+(12x^2+8x^2)+(9x-5x)+(-21+20)\qquad \text{Combine like terms} \\ &4x^3+20x^2+4x-1\qquad \qquad \qquad \qquad \qquad \qquad \; \; \; \text{Simplify} \end{align*}\]

Análise

Podemos verificar nossas respostas a esses tipos de problemas usando uma calculadora gráfica. Para verificar, faça um gráfico do problema conforme fornecido junto com a resposta simplificada. Os dois gráficos devem ser equivalentes. Certifique-se de usar a mesma janela para comparar os gráficos. Usar janelas diferentes pode fazer com que as expressões pareçam equivalentes quando não são.

Exercício$\PageIndex{2}$

Encontre a soma.

$(2x^3+5x^2−x+1)+(2x^2−3x−4)$

Resposta: $2x^3+7x^2−4x−3$

Exemplo$\PageIndex{3}$: Subtracting Polynomials

Descubra a diferença.

$(7x^4−x^2+6x+1)−(5x^3−2x^2+3x+2)$

Solução

$7x^4−5x^3+(−x^2+2x^2)+(6x−3x)+(1−2)$Combine termos semelhantes

$7x^4−5x^3+x^2+3x−1$Simplifique

Análise

Observe que encontrar a diferença entre dois polinômios é o mesmo que adicionar o oposto do segundo polinômio ao primeiro.

Exercício$\PageIndex{3}$

Descubra a diferença.

$(−7x^3−7x^2+6x−2)−(4x^3−6x^2−x+7)$

Resposta: $−11x^3−x^2+7x−9$

Multiplicação de polinômios

Multiplicar polinômios é um pouco mais desafiador do que adicionar e subtrair polinômios. Devemos usar a propriedade distributiva para multiplicar cada termo no primeiro polinômio por cada termo no segundo polinômio. Em seguida, combinamos termos semelhantes. Também podemos usar um atalho chamado método FOIL ao multiplicar binômios. Certos produtos especiais seguem padrões que podemos memorizar e usar em vez de multiplicar os polinômios manualmente a cada vez. Veremos várias maneiras de multiplicar polinômios.

Multiplicação de polinômios usando a propriedade distributiva

Para multiplicar um número por um polinômio, usamos a propriedade distributiva. O número deve ser distribuído para cada termo do polinômio. Podemos distribuir o$2$ in$2(x+7)$ para obter a expressão equivalente$2x+14$. Ao multiplicar polinômios, a propriedade distributiva nos permite multiplicar cada termo do primeiro polinômio por cada termo do segundo. Em seguida, adicionamos os produtos e combinamos termos semelhantes para simplificar.

Como: Dada a multiplicação de dois polinômios, use a propriedade distributiva para simplificar a expressão.

Multiplique cada termo do primeiro polinômio por cada termo do segundo.
Combine termos semelhantes.
Simplifique.

Exemplo$\PageIndex{4}$: Multiplying Polynomials Using the Distributive Property

Encontre o produto.

$(2x+1)(3x^2−x+4)$

Solução

\[\begin{align*} &2x(3x^2-x+4)+1(3x^2-x+4)\qquad \text{ Use the distributive property }\\ &(6x^3-2x^2+8x)+(3x^2-x+4)\qquad \text{ Multiply }\\ &6x^3+(-2x^2+3x^2)+(8x-x)+4\qquad \text{ Combine like terms } \\ &6x^3+x^2+7x+4\qquad \text{ Simplify } \end{align*}\]

Análise

Podemos usar uma tabela para acompanhar nosso trabalho, conforme mostrado na Tabela$\PageIndex{1}$. Escreva um polinômio na parte superior e o outro na lateral. Para cada caixa na tabela, multiplique o termo dessa linha pelo termo dessa coluna. Em seguida, adicione todos os termos, combine termos semelhantes e simplifique.

Tabela$\PageIndex{1}$
	$3x^2$	$−x$	$+4$
$2x$	$6x^3$	$−2x^2$	$8x$
$+1$	$3x^2$	$−x$	$4$

Exercício$\PageIndex{4}$

Encontre o produto.

$(3x+2)(x^3−4x^2+7)$

Resposta: $3x^4−10x^3−8x^2+21x+14$

Usando FOIL para multiplicar binômios

Às vezes, um atalho chamado FOIL é usado para encontrar o produto de dois binômios. É chamado FOIL porque multiplicamos os primeiros termos, os termos externos, os termos internos e depois os últimos termos de cada binômio.

$Duas quantidades entre parênteses estão sendo multiplicadas, a primeira sendo: a vezes x mais b e a segunda sendo: c vezes x mais d. Essa expressão é igual a ac vezes x ao quadrado mais ad vezes x mais bc vezes x mais bd. Os termos ax e cx são rotulados como: Primeiros termos. Os termos ax e d são rotulados como: Termos externos. Os termos b e cx são rotulados como: Termos internos. Os termos b e d são rotulados como: Últimos termos.$

O método FOIL surge da propriedade distributiva. Estamos simplesmente multiplicando cada termo do primeiro binômio por cada termo do segundo binômio e, em seguida, combinando termos semelhantes.

FOIL para simplificar a expressão

Dados dois binômios, use FOIL para simplificar a expressão.

Multiplique os termos externos dos binômios.
Multiplique os últimos termos de cada binômio.
Combine termos semelhantes e simplifique.

Exemplo$\PageIndex{5}$: Using FOIL to Multiply Binomials

Use FOIL para encontrar o produto.

$(2x−10)(3x+3) \nonumber$

Solução

Encontre o produto dos primeiros termos.

$alt$

Encontre o produto dos termos externos.

$alt$

Encontre o produto dos termos internos.

$alt$

Encontre o produto dos últimos termos.

$alt$

\[\begin{align*} &6x^2+6x-54x-54\qquad \text{Add the products}\\ &6x^2+(6x-54x)-54\qquad \text{Combine like terms} \\ &6x^2-48x-54\qquad \qquad \qquad \text{Simplify} \end{align*}\]

Exercício$\PageIndex{5}$

Use FOIL para encontrar o produto.

$(x+7)(3x−5)$

Resposta: $3x^2+16x−35$

Trinômios quadrados perfeitos

Certos produtos binomiais têm formas especiais. Quando um binômio é quadrado, o resultado é chamado de trinômio quadrado perfeito. Podemos encontrar o quadrado multiplicando o binômio por si só. No entanto, existe uma forma especial que cada um desses trinômios quadrados perfeitos assume, e a memorização da forma torna a quadratura dos binômios muito mais fácil e rápida. Vamos dar uma olhada em alguns trinômios quadrados perfeitos para nos familiarizarmos com o formulário.

${(x+5)}^2=x^2+10x+25$

${(x-3)}^2=x^2-6x+9$

${(4x-1)}^2=16x^2-8x+1$

Observe que o primeiro termo de cada trinômio é o quadrado do primeiro termo do binômio e, da mesma forma, o último termo de cada trinômio é o quadrado do último termo do binômio. O termo médio é o dobro do produto dos dois termos. Por fim, vemos que o primeiro sinal do trinômio é o mesmo do binômio.

Trinômios quadrados perfeitos

Quando um binômio é quadrado, o resultado é o primeiro termo ao quadrado adicionado para dobrar o produto de ambos os termos e o último termo ao quadrado.

\[{(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\]

Como: Dado um binômio, quadre-o usando a fórmula para trinômios quadrados perfeitos.

Efetue o quadrado do primeiro termo do binômio.
Efetue o quadrado do último termo do binômio.
Para o termo médio do trinômio, dobre o produto dos dois termos.
Adicione e simplifique.

Exemplo$\PageIndex{6}$: Expanding Perfect Squares

Expandir$(3x−8)^2$.

Solução

Comece dividindo o primeiro e o último termo ao quadrado. Para o termo médio do trinômio, dobre o produto dos dois termos.

\[\begin{align*} &{(3x)}^2-2(3x)(8)+{(-8)}^2 \\ &9x^2-48x+64\qquad \qquad \; \; \; \; \text{Simplify} \end{align*}\]

Exercício$\PageIndex{6}$

Expandir${(4x−1)}^2$.

Resposta: $16x^2−8x+1$

Diferença de quadrados

Outro produto especial é chamado de diferença de quadrados, que ocorre quando multiplicamos um binômio por outro binômio com os mesmos termos, mas com o sinal oposto. Vamos ver o que acontece quando multiplicamos$(x+1)(x−1)$ usando o método FOIL.

\[\begin{align*} (x+1)(x-1) &= x^2-x+x-1\\ &= x^2-1 \end{align*}\]

O termo intermediário desaparece, resultando em uma diferença de quadrados. Assim como fizemos com os quadrados perfeitos, vamos ver alguns exemplos.

$(x+5)(x-5)=x^2-25$

$(x+11)(x-11)=x^2-121$

$(2x+3)(2x-3)=4x^2-9$

Como o sinal muda no segundo binômio, os termos externo e interno se cancelam, e ficamos apenas com o quadrado do primeiro termo menos o quadrado do último termo.

PERGUNTAS E RESPOSTAS

Existe um formulário especial para a soma dos quadrados?

Não. A diferença dos quadrados ocorre porque os sinais opostos dos binômios fazem com que os termos médios desapareçam. Não há dois binômios que se multipliquem para igualar a soma dos quadrados.

Diferença de quadrados

Quando um binômio é multiplicado por um binômio com os mesmos termos separados pelo sinal oposto, o resultado é o quadrado do primeiro termo menos o quadrado do último termo.

\[(a+b)(a−b)=a^2−b^2\]

Como fazer: Dado um binômio multiplicado por um binômio com os mesmos termos, mas com o sinal oposto, encontre a diferença dos quadrados.

Efetue o quadrado do primeiro termo dos binômios.
Efetue o quadrado do último termo dos binômios.
Subtraia o quadrado do último termo do quadrado do primeiro termo.

Exemplo$\PageIndex{7}$: Multiplying Binomials Resulting in a Difference of Squares

Multiplique$(9x+4)(9x−4)$.

Solução

Elabore o primeiro termo a ser obtido${(9x)}^2=81x^2$. Elabore o último termo a ser obtido$4^2=16$. Subtraia o quadrado do último termo do quadrado do primeiro termo para encontrar o produto de$81x^2−16$.

Exercício$\PageIndex{7}$

Multiplique$(2x+7)(2x−7)$.

Resposta: $4x^2−49$

Executando operações com polinômios de várias variáveis

Examinamos polinômios contendo apenas uma variável. No entanto, um polinômio pode conter várias variáveis. Todas as mesmas regras se aplicam ao trabalhar com polinômios contendo várias variáveis. Considere um exemplo:

\[\begin{align*} &(a+2b)(4a-b-c) a(4a-b-c)+2b(4a-b-c)\qquad \text{ Use the distributive property }\\ &4a^2-ab-ac+8ab-2b^2-2bc\qquad \qquad\qquad\qquad\qquad \text{ Multiply }\\ &4a^2+(-ab+8ab)-ac-2b^2-2bc\qquad \qquad\qquad\qquad \; \text{ Combine like terms } \\ &4a^2+7ab-ac-2bc-2b^2\qquad \qquad \qquad \qquad \qquad \qquad\text{ Simplify } \end{align*}\]

Exemplo$\PageIndex{8}$: Multiplying Polynomials Containing Several Variables

Multiplique$(x+4)(3x−2y+5)$.

Solução

\[\begin{align*} &x(3x-2y+5)+4(3x-2y+5)\qquad \text{ Use the distributive property }\\ &3x^2-2xy+5x+12x-8y+20\qquad \text{ Multiply }\\ &3x^2-2xy+(5x+12x)-8y+20\qquad \text{ Combine like terms } \\ &3x^2-2xy+17x-8y+20\qquad \qquad\text{ Simplify } \end{align*}\]

Exercício$\PageIndex{8}$

Multiplique$(3x−1)(2x+7y−9)$.

Resposta: $6x^2+21xy−29x−7y+9$

Mídia

Acesse esses recursos on-line para obter instruções e práticas adicionais com polinômios.

Equações-chave

trinômio quadrado perfeito	${(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2$
diferença de quadrados	$(a+b)(a−b)=a^2−b^2$

Conceitos-chave

Um polinômio é uma soma de termos, cada um consistindo em uma variável elevada a uma potência inteira não negativa. O grau é a maior potência da variável que ocorre no polinômio. O termo principal é o termo que contém o grau mais alto e o coeficiente principal é o coeficiente desse termo. Veja o exemplo.
Podemos somar e subtrair polinômios combinando termos semelhantes. Veja o exemplo e o exemplo.
Para multiplicar polinômios, use a propriedade distributiva para multiplicar cada termo no primeiro polinômio por cada termo no segundo. Em seguida, adicione os produtos. Veja o exemplo.
FOIL (First, Outer, Inner, Last) é um atalho que pode ser usado para multiplicar binômios. Veja o exemplo.
Trinômios quadrados perfeitos e diferença de quadrados são produtos especiais. Veja o exemplo e o exemplo.
Siga as mesmas regras para trabalhar com polinômios contendo várias variáveis. Veja o exemplo.

	\(3x^2\)	\(−x\)	\(+4\)
\(2x\)	\(6x^3\)	\(−2x^2\)	\(8x\)
\(+1\)	\(3x^2\)	\(−x\)	\(4\)

Polinômios

Como: Dada uma expressão polinomial, identifique o grau e o coeficiente principal.

Exemplo\(\PageIndex{1}\): Identifying the Degree and Leading Coefficient of a Polynomial

Exercício\(\PageIndex{1}\)

Como: Dados vários polinômios, adicione ou subtraia para simplificar as expressões.

Exemplo\(\PageIndex{2}\): Adding Polynomials

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\): Subtracting Polynomials

Exercício\(\PageIndex{3}\)

Como: Dada a multiplicação de dois polinômios, use a propriedade distributiva para simplificar a expressão.

Exemplo\(\PageIndex{4}\): Multiplying Polynomials Using the Distributive Property

Exercício\(\PageIndex{4}\)

FOIL para simplificar a expressão

Exemplo\(\PageIndex{5}\): Using FOIL to Multiply Binomials

Exercício\(\PageIndex{5}\)

Trinômios quadrados perfeitos

Como: Dado um binômio, quadre-o usando a fórmula para trinômios quadrados perfeitos.

Exemplo\(\PageIndex{6}\): Expanding Perfect Squares

Exercício\(\PageIndex{6}\)

PERGUNTAS E RESPOSTAS

Diferença de quadrados

Como fazer: Dado um binômio multiplicado por um binômio com os mesmos termos, mas com o sinal oposto, encontre a diferença dos quadrados.

Exemplo\(\PageIndex{7}\): Multiplying Binomials Resulting in a Difference of Squares

Exercício\(\PageIndex{7}\)

Exemplo\(\PageIndex{8}\): Multiplying Polynomials Containing Several Variables

Exercício\(\PageIndex{8}\)

Mídia

Equações-chave

Conceitos-chave

trinômio quadrado perfeito	\({(x+a)}^2=(x+a)(x+a)=x^2+2ax+a^2\)
diferença de quadrados	\((a+b)(a−b)=a^2−b^2\)