Skip to main content
Global

2.5: Gráficos de caixas

  1. Last updated
  2. Save as PDF
  • Page ID
    190100

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Os gráficos de caixa (também chamados de gráficos box-and-whisker ou de box-whisker) fornecem uma boa imagem gráfica da concentração dos dados. Eles também mostram a que distância os valores extremos estão da maioria dos dados. Um gráfico de caixa é construído a partir de cinco valores: o valor mínimo, o primeiro quartil, a mediana, o terceiro quartil e o valor máximo. Usamos esses valores para comparar a proximidade de outros valores de dados.

    Para construir um gráfico de caixa, use uma linha numérica horizontal ou vertical e uma caixa retangular. Os menores e maiores valores de dados rotulam as extremidades do eixo. O primeiro quartil marca uma extremidade da caixa e o terceiro quartil marca a outra extremidade da caixa. Aproximadamente 50% do meio dos dados estão dentro da caixa. Os “bigodes” se estendem das extremidades da caixa até os menores e maiores valores de dados. A mediana ou o segundo quartil pode estar entre o primeiro e o terceiro quartis, ou pode ser um, ou o outro, ou ambos. O gráfico da caixa fornece uma imagem boa e rápida dos dados.

    Você pode encontrar gráficos de caixa e bigode com pontos marcando valores atípicos. Nesses casos, os bigodes não estão se estendendo aos valores mínimo e máximo.

    Considere, novamente, esse conjunto de dados.

    1; 1; 2; 2; 4; 6; 6; 8; 7,2; 8; 8,3; 9; 10; 10; 11,5

    O primeiro quartil é dois, a mediana é sete e o terceiro quartil é nove. O menor valor é um e o maior valor é 11,5. A imagem a seguir mostra o gráfico da caixa construída.

    Veja as instruções da calculadora no site da TI ou no apêndice.

    O primeiro bigode do boxplot horizontal se estende do menor valor, 1, até o primeiro quartil, 2, a caixa começa no primeiro quartil e se estende até o terceiro quartil, 9, uma linha tracejada vertical é desenhada na mediana, 7, e o segundo bigode se estende do terceiro quartil até o maior valor de 11,5.
    Figura\(\PageIndex{1}\)

    Os dois bigodes se estendem do primeiro quartil ao menor valor e do terceiro quartil ao maior valor. A mediana é mostrada com uma linha tracejada.

    É importante iniciar um gráfico de caixa com uma linha numérica em escala. Caso contrário, o gráfico da caixa pode não ser útil.

    Exemplo\(\PageIndex{1}\)

    Os dados a seguir são as alturas de 40 alunos em uma aula de estatística.

    59; 60; 61; 62; 62; 63; 63; 64; 64; 64; 65; 65; 65; 65; 65; 65; 65; 65; 65; 65; 66; 66; 67; 67; 68; 68; 69; 70; 70; 70; 70; 70; 71; 71; 72; 72; 73; 74; 74; 75; 77

    Crie um gráfico de caixa com as seguintes propriedades; as instruções da calculadora para os valores mínimo e máximo, bem como os quartis, seguem o exemplo.

    • Valor mínimo = 59
    • Valor máximo = 77
    • Q 1: Primeiro quartil = 64,5
    • Q 2: Segundo quartil ou mediana = 66
    • Q 3: Terceiro quartil = 70
    Boxplot horizontal com o primeiro bigode que se estende do menor valor, 59, até Q1, 64,5, caixa começando de Q1 a Q3, 70, linha tracejada mediana em Q2, 66 e segundo bigode se estendendo de Q3 até o maior valor, 77.
    Figura\(\PageIndex{2}\)
    1. Cada trimestre tem aproximadamente 25% dos dados.
    2. Os spreads dos quatro trimestres são 64,5 — 59 = 5,5 (primeiro trimestre), 66 — 64,5 = 1,5 (segundo trimestre), 70 — 66 = 4 (terceiro trimestre) e 77 — 70 = 7 (quarto trimestre). Portanto, o segundo trimestre tem o menor spread e o quarto trimestre tem o maior spread.
    3. \(\text{Range} = \text{maximum value} - \text{the minimum value} = 77 - 59 = 18\)
    4. Intervalo interquartil:\(IQR = Q_{3} – Q_{1} = 70 - 64.5 = 5.5\).
    5. O intervalo 59—65 tem mais de 25% dos dados, portanto, contém mais dados do que o intervalo 66 a 70, que contém 25% dos dados.
    6. Os 50% médios (metade média) dos dados têm um intervalo de 5,5 polegadas.

    Calculadora

    Para encontrar o mínimo, o máximo e os quartis:

    Insira os dados no editor de listas (pressione STAT 1:EDIT). Se precisar limpar a lista, direcione até o nome L1, pressione CLEAR e, em seguida, seta para baixo.

    Coloque os valores dos dados na lista L1.

    Pressione STAT e seta para CALC. Pressione 1:1 -VARStats. Digite L1.

    Pressione ENTER.

    Use as teclas de seta para baixo e para cima para rolar.

    Menor valor = 59.

    Maior valor = 77.

    Q 1: Primeiro quartil = 64,5.

    Q 2: Segundo quartil ou mediana = 66.

    Q 3: Terceiro quartil = 70.

    Para construir o gráfico de caixa:

    Pressione 4: Plotsoff. Pressione ENTER.

    Seta para baixo e, em seguida, use a tecla de seta para a direita para ir para a quinta imagem, que é o gráfico da caixa. Pressione ENTER.

    Seta para baixo até Xlist: pressione 2nd 1 para L1

    Seta para baixo até Freq: Pressione ALPHA. Pressione 1.

    Pressione Zoom. Pressione 9: ZoomStat.

    Pressione TRACE e use as teclas de seta para examinar o gráfico da caixa.

    Exercício\(\PageIndex{1}\)

    Os dados a seguir são o número de páginas em 40 livros em uma prateleira. Construa um gráfico de caixa usando uma calculadora gráfica e indique o intervalo interquartil.

    136; 140; 178; 190; 205; 215; 217; 218; 232; 234; 240; 255; 270; 275; 290; 301; 303; 315; 317; 318; 326; 333; 343; 349; 360; 369; 377; 388; 391; 392; 398; 400; 402; 405; 408; 490; 22; 429; 450; 475; 512

    Resposta

    Figura\(\PageIndex{3}\)

    \(IQR = 158\)

    Para alguns conjuntos de dados, alguns dos maiores valores, menores valores, primeiro quartil, mediana e terceiro quartil podem ser os mesmos. Por exemplo, você pode ter um conjunto de dados no qual a mediana e o terceiro quartil são iguais. Nesse caso, o diagrama não teria uma linha pontilhada dentro da caixa exibindo a mediana. O lado direito da caixa exibiria tanto o terceiro quartil quanto a mediana. Por exemplo, se o menor valor e o primeiro quartil fossem um, a mediana e o terceiro quartil fossem ambos cinco e o maior valor fosse sete, o gráfico de caixa teria a seguinte aparência:

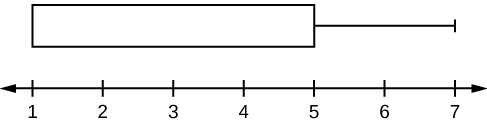
    A caixa boxplot horizontal começa no menor valor e Q1, 1, até Q3 e mediana, 5, nenhuma linha mediana é designada, e tem seu único bigode se estendendo do Q3 até o maior valor, 7.
    Figura\(\PageIndex{4}\)

    Nesse caso, pelo menos 25% dos valores são iguais a um. Vinte e cinco por cento dos valores estão entre um e cinco, inclusive. Pelo menos 25% dos valores são iguais a cinco. Os 25% superiores dos valores ficam entre cinco e sete, inclusive.

    Exemplo\(\PageIndex{2}\)

    Os resultados dos testes de uma aula de estatística da faculdade ministrada durante o dia são:

    99; 56; 78; 55,5; 32; 90; 80; 81; 56; 59; 45; 77; 84,5; 84; 70; 72; 68; 32; 79; 90

    Os resultados dos testes de uma aula de estatística da faculdade ministrada durante a noite são:

    98; 78; 68; 83; 81; 89; 88; 76; 65; 45; 98; 90; 80; 84,5; 85; 79; 78; 98; 90; 79; 81; 25,5

    1. Encontre os menores e maiores valores, a mediana e o primeiro e o terceiro quartil da classe diurna.
    2. Encontre os menores e maiores valores, a mediana e o primeiro e o terceiro quartil para a classe noturna.
    3. Para cada conjunto de dados, qual porcentagem dos dados está entre o menor valor e o primeiro quartil? o primeiro quartil e a mediana? a mediana e o terceiro quartil? o terceiro quartil e o maior valor? Qual porcentagem dos dados está entre o primeiro quartil e o maior valor?
    4. Crie um gráfico de caixa para cada conjunto de dados. Use uma linha numérica para os dois gráficos de caixa.
    5. Qual gráfico de caixa tem a distribuição mais ampla para os 50% médios dos dados (os dados entre o primeiro e o terceiro quartis)? O que isso significa para esse conjunto de dados em comparação com o outro conjunto de dados?

    Resposta

      • Mín = 32
      • Q 1 = 56
      • M = 74,5
      • Q 3 = 82,5
      • Máximo = 99
      • Mín = 25,5
      • Q 1 = 78
      • M = 81
      • Q 3 = 89
      • Máximo = 98
    3. Aula diurna: Existem seis valores de dados que variam de 32 a 56:30%. Existem seis valores de dados que variam de 56 a 74,5:30%. Existem cinco valores de dados que variam de 74,5 a 82,5:25%. Existem cinco valores de dados que variam de 82,5 a 99:25%. Há 16 valores de dados entre o primeiro quartil, 56, e o maior valor, 99:75%. Aula noturna:

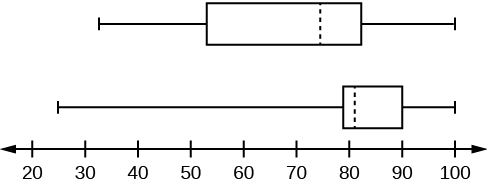
    4. Dois gráficos de caixa sobre uma linha numérica de 0 a 100. O gráfico superior mostra um bigode de 32 a 56, uma linha sólida em 56, uma linha tracejada em 74,5, uma linha sólida em 82,5 e um bigode de 82,5 a 99. O gráfico inferior mostra um bigode de 25,5 a 78, linha sólida em 78, linha tracejada em 81, linha sólida em 89 e um bigode de 89 a 98.

      Figura\(\PageIndex{5}\)

    5. O primeiro conjunto de dados tem uma distribuição mais ampla para os 50% médios dos dados. O IQR do primeiro conjunto de dados é maior do que o IQR do segundo conjunto. Isso significa que há mais variabilidade no meio de 50% do primeiro conjunto de dados.

    Exercício\(\PageIndex{2}\)

    O conjunto de dados a seguir mostra as alturas em polegadas para os meninos em uma turma de 40 alunos.

    66; 66; 67; 67; 68; 68; 68; 68; 68; 69; 69; 69; 70; 71; 72; 72; 72; 73; 73; 74

    O conjunto de dados a seguir mostra as alturas em polegadas para as meninas em uma turma de 40 alunos.

    61; 61; 62; 62; 63; 63; 63; 65; 65; 65; 66; 66; 66; 67; 68; 68; 68; 69; 69; 69; 69

    Construa um gráfico de caixa usando uma calculadora gráfica para cada conjunto de dados e indique qual gráfico de caixa tem a distribuição mais ampla para os 50% médios dos dados.

    Resposta

    Figura\(\PageIndex{6}\)

    IQR para meninos = 4

    IQR para meninas = 5

    O gráfico da caixa para as alturas das meninas tem uma distribuição mais ampla para 50% médios dos dados.

    Exemplo\(\PageIndex{3}\)

    Faça um gráfico gráfico de um gráfico em forma de caixa para os valores de dados mostrados.

    10; 10; 10; 15; 35; 75; 90; 95; 100; 175; 420; 490; 515; 515; 790

    Os cinco números usados para criar um gráfico de caixa e bigode são:

    • Min: 10
    • Q 1: 15
    • Med: 95
    • Q 3: 490
    • Máximo: 790

    O gráfico a seguir mostra o gráfico de caixa e bigode.

    Figura\(\PageIndex{7}\)

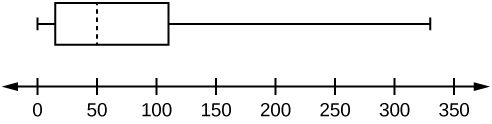
    Exercício\(\PageIndex{3}\)

    Siga as etapas que você usou para representar graficamente um gráfico de caixa e bigode para os valores de dados mostrados.

    0; 5; 5; 15; 30; 30; 45; 50; 50; 60; 75; 110; 140; 240; 330

    Resposta

    Os dados estão em ordem do mínimo para o maior. Existem 15 valores, então o oitavo número em ordem é a mediana: 50. Há sete valores de dados gravados à esquerda da mediana e 7 valores à direita. Os cinco valores usados para criar o boxplot são:

    • Min: 0
    • Q 1: 15
    • Med: 50
    • Q 3: 110
    • Máximo: 330
    Figura\(\PageIndex{8}\)

    Referências

    1. Dados da West Magazine.

    Revisão

    Os gráficos de caixa são um tipo de gráfico que pode ajudar a organizar visualmente os dados. Para representar graficamente um gráfico de caixa, os seguintes pontos de dados devem ser calculados: o valor mínimo, o primeiro quartil, a mediana, o terceiro quartil e o valor máximo. Depois que o gráfico da caixa for representado graficamente, você poderá exibir e comparar distribuições de dados.

    Sessenta e cinco vendedores de carros selecionados aleatoriamente foram questionados sobre o número de carros que eles geralmente vendem em uma semana. Quatorze pessoas responderam que geralmente vendem três carros; dezenove geralmente vendem quatro carros; doze geralmente vendem cinco carros; nove geralmente vendem seis carros; onze geralmente vendem sete carros.

    Exercício 2.5.4

    Construa um gráfico de caixa abaixo. Use uma régua para medir e dimensionar com precisão.

    Exercício 2.5.5

    Observando seu gráfico de caixa, parece que os dados estão concentrados juntos, distribuídos uniformemente ou concentrados em algumas áreas, mas não em outras? Como você pode saber?

    Resposta

    Mais de 25% dos vendedores vendem quatro carros em uma semana normal. Você pode ver essa concentração no gráfico de caixa porque o primeiro quartil é igual à mediana. Os 25% superiores e os 25% inferiores estão espalhados uniformemente; os bigodes têm o mesmo comprimento.

    Reunindo tudo

    Exercício 2.5.6

    O Condado de Santa Clara, Califórnia, tem aproximadamente 27.873 nipo-americanos. Suas idades são as seguintes:

    Faixa etária Porcentagem da comunidade
    0—17 18,9
    18—24 8.0
    25—34 22,8
    35—44 15,0
    45—54 13.1
    55—64 11,9
    65+ 10.3
    1. Construa um histograma da comunidade nipo-americana no Condado de Santa Clara, CA. As barras não terão a mesma largura neste exemplo. Por que não? Que impacto isso tem na confiabilidade do gráfico?
    2. Qual porcentagem da comunidade tem menos de 35 anos?
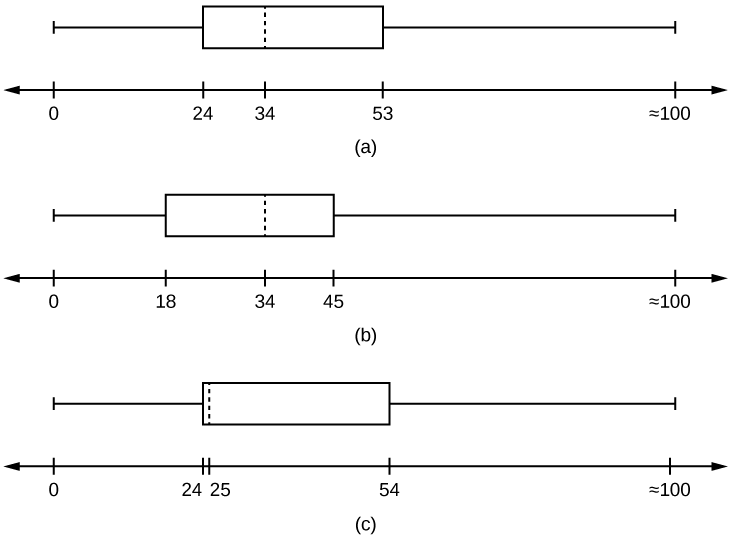
    3. Qual gráfico de caixa se assemelha mais às informações acima?
    Três gráficos de caixa com valores entre 0 e 100. O lote i tem Q1 em 24, M em 34 e Q3 em 53; o lote ii tem Q1 em 18, M em 34 e Q3 em 45; o lote iii tem Q1 em 24, M em 25 e Q3 em 54.
    Figura\(\PageIndex{9}\).

    Resposta

    1. Para obter um gráfico, verifique a solução do aluno.
    2. 49,7% da comunidade tem menos de 35 anos.
    3. Com base nas informações da tabela, o gráfico (a) representa mais de perto os dados.

    Glossário

    Gráfico da caixa
    um gráfico que fornece uma visão rápida dos 50% médios dos dados
    Primeiro quartil
    o valor que é a mediana da metade inferior do conjunto de dados ordenado
    Polígono de frequência
    parece um gráfico de linhas, mas usa intervalos para exibir intervalos de grandes quantidades de dados
    Intervalo
    também chamado de intervalo de classe; um intervalo representa um intervalo de dados e é usado para exibir grandes conjuntos de dados
    Conjunto de dados emparelhado
    dois conjuntos de dados que têm uma relação de um para um, de forma que:
    • ambos os conjuntos de dados têm o mesmo tamanho e
    • cada ponto de dados em um conjunto de dados é combinado com exatamente um ponto do outro conjunto.
    Distorcido
    usado para descrever dados que não são simétricos; quando o lado direito de um gráfico parece “cortado” em comparação com o lado esquerdo, dizemos que ele está “inclinado para a esquerda”. Quando o lado esquerdo do gráfico parece “cortado” em comparação com o lado direito, dizemos que os dados estão “distorcidos para a direita”. Como alternativa: quando os valores mais baixos dos dados estão mais espalhados, dizemos que os dados estão distorcidos para a esquerda. Quando os valores maiores estão mais dispersos, os dados são distorcidos para a direita.