19.2: Examinando as estrelas

Objetivos de

Ao final desta seção, você poderá:

• Entenda o conceito de triangular distâncias para objetos distantes, incluindo estrelas
• Explique por que os satélites espaciais oferecem distâncias mais precisas do que os métodos terrestres
• Discuta os esforços dos astrônomos para estudar as estrelas mais próximas do Sol

É um passo enorme ir dos planetas às estrelas. Por exemplo, nossa sonda Voyager 1, lançada em 1977, agora viajou mais longe da Terra do que qualquer outra espaçonave. Como está escrito em 2016, a Voyager 1 está a 134 UA do Sol. ¹ A estrela mais próxima, no entanto, está a centenas de milhares de UA da Terra. Mesmo assim, podemos, em princípio, pesquisar distâncias até as estrelas usando a mesma técnica que um engenheiro civil emprega para pesquisar a distância até uma montanha ou árvore inacessível — o método de triangulação.

Triangulação no espaço

Um exemplo prático de triangulação é sua própria percepção de profundidade. Como você tem o prazer de descobrir todas as manhãs ao se olhar no espelho, seus dois olhos estão localizados a uma certa distância. Portanto, você vê o mundo de dois pontos de vista diferentes, e é essa perspectiva dupla que permite que você tenha uma noção geral de quão distantes os objetos estão.

Para ver o que queremos dizer, pegue uma caneta e segure-a alguns centímetros na frente do seu rosto. Olhe primeiro com um olho (fechando o outro) e depois troque os olhos. Observe como a caneta parece se deslocar em relação aos objetos na sala. Agora segure a caneta no comprimento do braço: a mudança é menor. Se você brincar com a movimentação da caneta por um tempo, notará que quanto mais longe a segurar, menos ela parecerá se deslocar. Seu cérebro realiza automaticamente essas comparações e dá uma boa noção de quão distantes as coisas estão em sua vizinhança imediata.

Se seus braços fossem feitos de borracha, você poderia esticar a caneta longe o suficiente dos olhos para que a mudança se tornasse imperceptível. Isso ocorre porque nossa percepção de profundidade falha em objetos a mais de algumas dezenas de metros de distância. Para ver o deslocamento de um objeto a um quarteirão ou mais de você, seus olhos precisariam se afastar muito mais.

Vamos ver como os topógrafos aproveitam a mesma ideia. Suponha que você esteja tentando medir a distância de uma árvore em um rio profundo (Figura\(\PageIndex{1}\)). Você configurou duas estações de observação a uma certa distância. Essa distância (linha AB na Figura\(\PageIndex{1}\)) é chamada de linha de base. Agora, a direção da árvore (C na figura) em relação à linha de base é observada em cada estação. Observe que C aparece em direções diferentes das duas estações. Essa aparente mudança na direção do objeto remoto devido a uma mudança no ponto de vista do observador é chamada de paralaxe.

\(\PageIndex{1}\)Triangulação de figuras. A triangulação nos permite medir distâncias até objetos inacessíveis. Ao obter o ângulo de uma árvore a partir de dois pontos de vista diferentes, podemos calcular as propriedades do triângulo que elas formam e, portanto, a distância até a árvore.

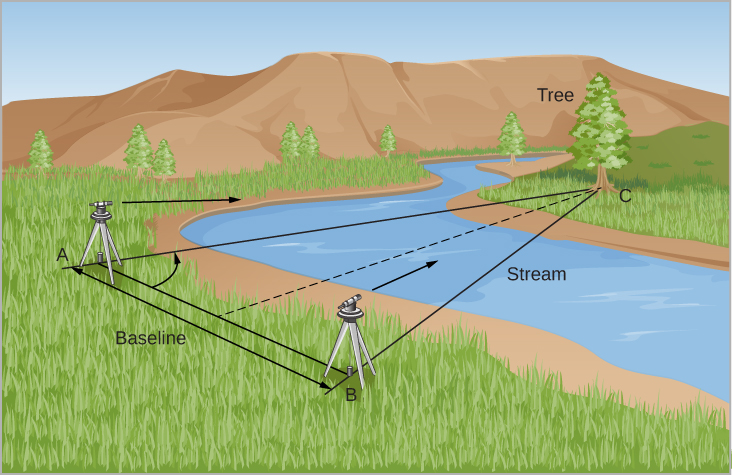
A paralaxe também é o ângulo que as linhas AC e BC formam — em termos matemáticos, o ângulo subtendido pela linha de base. O conhecimento dos ângulos em A e B e do comprimento da linha de base, AB, permite que o triângulo ABC seja resolvido para qualquer uma de suas dimensões — digamos, a distância AC ou BC. A solução pode ser alcançada construindo um desenho em escala ou usando trigonometria para fazer um cálculo numérico. Se a árvore estivesse mais distante, todo o triângulo seria mais longo e mais fino, e o ângulo de paralaxe seria menor. Assim, temos a regra geral de que quanto menor a paralaxe, mais distante deve estar o objeto que estamos medindo.

Na prática, os tipos de linhas de base que os topógrafos usam para medir distâncias na Terra são completamente inúteis quando tentamos medir distâncias no espaço. Quanto mais distante estiver um objeto astronômico, maior deve ser a linha de base para nos dar uma chance razoável de fazer uma medição. Infelizmente, quase todos os objetos astronômicos estão muito distantes. Medir suas distâncias requer uma linha de base muito grande e medições angulares altamente precisas. A Lua é o único objeto próximo o suficiente para que sua distância possa ser encontrada com bastante precisão com medições feitas sem um telescópio. Ptolomeu determinou a distância até a Lua corretamente até alguns por cento. Ele usou a própria Terra giratória como linha de base, medindo a posição da Lua em relação às estrelas em dois momentos diferentes da noite.

Com a ajuda de telescópios, astrônomos posteriores foram capazes de medir as distâncias até os planetas e asteróides mais próximos usando o diâmetro da Terra como linha de base. Foi assim que a UA foi estabelecida pela primeira vez. Alcançar as estrelas, no entanto, requer uma linha de base muito mais longa para triangulação e medições extremamente sensíveis. Essa linha de base é fornecida pela viagem anual da Terra ao redor do Sol.

Distâncias às estrelas

À medida que a Terra viaja de um lado de sua órbita para o outro, ela graciosamente nos fornece uma linha de base de 2 UA, ou cerca de 300 milhões de quilômetros. Embora essa seja uma linha de base muito maior do que o diâmetro da Terra, as estrelas estão tão distantes que a mudança de paralaxe resultante ainda não é visível a olho nu — nem mesmo para as estrelas mais próximas.

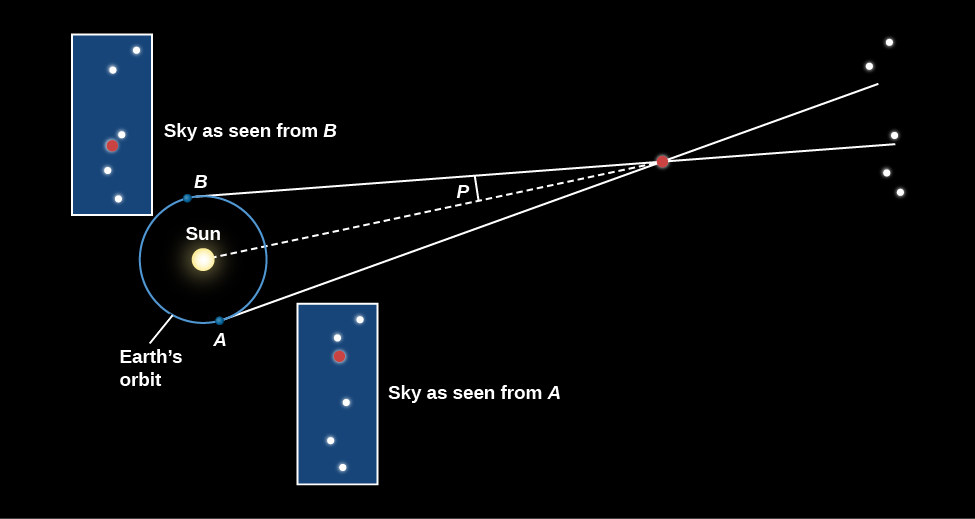
No capítulo “Observando o Céu: O Nascimento da Astronomia”, discutimos como esse dilema deixou perplexos os antigos gregos, alguns dos quais na verdade sugeriram que o Sol poderia ser o centro do sistema solar, com a Terra em movimento ao seu redor. Aristóteles e outros argumentaram, no entanto, que a Terra não poderia estar girando em torno do Sol. Se fosse, disseram eles, certamente observaríamos a paralaxe das estrelas mais próximas contra o fundo de objetos mais distantes enquanto víamos o céu de diferentes partes da órbita da Terra (Figura\(\PageIndex{3}\)). Tycho Brahe (1546—1601) apresentou o mesmo argumento incorreto quase 2000 anos depois, quando suas medidas cuidadosas das posições estelares a olho nu não revelaram essa mudança.

Esses primeiros observadores não perceberam o quão realmente distantes as estrelas estavam e quão pequena era a mudança em suas posições, mesmo com toda a órbita da Terra como linha de base. O problema era que eles não tinham ferramentas para medir mudanças de paralaxe muito pequenas para serem vistas com o olho humano. No século XVIII, quando não havia mais dúvidas sérias sobre a revolução da Terra, ficou claro que as estrelas deveriam estar extremamente distantes. Astrônomos equipados com telescópios começaram a criar instrumentos capazes de medir as pequenas mudanças de estrelas próximas em relação ao fundo de objetos celestes mais distantes (e, portanto, inalteráveis).

Esse foi um desafio técnico significativo, pois, mesmo para as estrelas mais próximas, os ângulos de paralaxe geralmente são apenas uma fração de segundo de arco. Lembre-se de que um segundo de arco (arcsec) é um ângulo de apenas 1/3600 de um grau. Uma moeda do tamanho de um quarto dos EUA pareceria ter um diâmetro de 1 arco-segundo se você a estivesse vendo a uma distância de cerca de 5 quilômetros (3 milhas). Pense em quão pequeno é esse ângulo. Não é de admirar que os astrônomos tenham levado muito tempo até que pudessem medir mudanças tão pequenas.

As primeiras detecções bem-sucedidas de paralaxe estelar foram no ano de 1838, quando Friedrich Bessel na Alemanha (Figura\(\PageIndex{2}\)), Thomas Henderson, um astrônomo escocês trabalhando no Cabo da Boa Esperança, e Friedrich Struve na Rússia mediram de forma independente as paralaxes das estrelas 61 Cygni, Alpha Centauri, e Vega, respectivamente. Até mesmo a estrela mais próxima, Alpha Centauri, mostrou um deslocamento total de apenas cerca de 1,5 segundos de arco ao longo de um ano.

Figura\(\PageIndex{2}\) Friedrich Wilhelm Bessel (1784-1846), Thomas J. Henderson (1798—1844) e Friedrich Struve (1793-1864). (a) Bessel fez a primeira medição autenticada da distância até uma estrela (61 Cygni) em 1838, um feito que escapou de muitos astrônomos dedicados por quase um século. Mas outros dois, (b) o astrônomo escocês Thomas J. Henderson e (c) Friedrich Struve, na Rússia, estavam por perto.

A figura\(\PageIndex{3}\) mostra como essas medições funcionam. Vista de lados opostos da órbita da Terra, uma estrela próxima muda de posição quando comparada a um padrão de estrelas mais distantes. Na verdade, os astrônomos definem paralaxe como metade do ângulo que uma estrela muda quando vista de lados opostos da órbita da Terra (o ângulo identificado como P na Figura\(\PageIndex{3}\)). A razão para essa definição é apenas que eles preferem lidar com uma linha de base de 1 UA em vez de 2 AU.

Figura\(\PageIndex{3}\) Parallax., À medida que a Terra gira em torno do Sol, a direção na qual vemos uma estrela próxima varia em relação às estrelas distantes. Definimos a paralaxe da estrela próxima como metade da mudança total na direção e geralmente a medimos em segundos de arco.

Unidades de distância estelar

Com uma linha de base de uma UA, a que distância uma estrela teria que estar para ter uma paralaxe de 1 arco-segundo? A resposta acaba sendo 206.265 UA, ou 3,26 anos-luz. Isso é igual a 3,1 × 10 ¹³ quilômetros (em outras palavras, 31 trilhões de quilômetros). Damos a esta unidade um nome especial, o parsec (pc) — derivado da “distância na qual temos um par allax de um segundo”. A distância (\(D\)) de uma estrela em parsecs é apenas o inverso de sua paralaxe (p) em segundos de arco; ou seja,

\[D=\frac{1}{p} \nonumber\]

Assim, uma estrela com uma paralaxe de 0,1 arco-segundo seria encontrada a uma distância de 10 parsecs, e uma com paralaxe de 0,05 arco-segundo estaria a 20 parsecs de distância.

Na época em que a maioria de nossas distâncias vinha de medições de paralaxe, um parsec era uma unidade de distância útil, mas não é tão intuitivo quanto o ano-luz. Uma vantagem do ano-luz como unidade é que ele enfatiza o fato de que, ao olharmos para o espaço, também estamos olhando para o tempo. A luz que vemos de uma estrela a 100 anos-luz de distância deixou essa estrela há 100 anos. O que estudamos não é a estrela como ela é agora, mas sim como era no passado. A luz que chega aos nossos telescópios hoje de galáxias distantes os deixou antes mesmo da Terra existir.

Neste texto, usaremos anos-luz como nossa unidade de distância, mas muitos astrônomos ainda usam parsecs quando escrevem artigos técnicos ou conversam entre si em reuniões. Para converter entre as duas unidades de distância, lembre-se: 1 parsec = 3,26 ano-luz e 1 ano-luz = 0,31 parsec.

Exemplo\(\PageIndex{1}\): Qual é a distância de um ano-luz?

Um ano-luz é a distância que a luz percorre em 1 ano. Dado que a luz viaja a uma velocidade de 300.000 km/s, quantos quilômetros existem em um ano-luz?

Solução

Aprendemos anteriormente que velocidade = distância/tempo. Podemos reorganizar essa equação para que\(\text{distance } = \text{ velocity } \times \text{ time }\). Agora, precisamos determinar o número de segundos em um ano.

Há aproximadamente 365 dias em 1 ano. Para determinar o número de segundos, devemos estimar o número de segundos em 1 dia.

Podemos alterar as unidades da seguinte forma (observe como as unidades de tempo são canceladas):

\[ 1 \text{ day } \times 24 \text{ hr/day } \times 60 \text{ min/hr } \times 60 \text{ s/min } = 86,400 \text{ s/day} \nonumber\]

Em seguida, para obter o número de segundos por ano:

\[ 365 \text{ days/year } \times 86,400 \text{ s/day } = 31,536,000 \text{ s/year} \nonumber\]

Agora podemos multiplicar a velocidade da luz pelo número de segundos por ano para obter a distância percorrida pela luz em 1 ano:

\[ \begin{aligned} \text{distance } & = \text{ velocity } \times \text{ time} \\ & = 300,000 \text{ km/s } \times 31,536,000 \text{ s} \\ & =9.46 \times 10^{12} \text{ km} \end{aligned} \nonumber\]

São quase 10.000.000.000.000 km que a luz cobre em um ano. Para ajudá-lo a imaginar o tamanho dessa distância, mencionaremos que uma corda de 1 ano-luz de comprimento poderia caber em torno da circunferência da Terra 236 milhões de vezes.

Exercício\(\PageIndex{1}\)

O número acima é muito grande. O que acontece se colocarmos isso em termos que possam ser um pouco mais compreensíveis, como o diâmetro da Terra? O diâmetro da Terra é de cerca de 12.700 km.

Responda

\[ \begin{aligned} 1 \text{ light-year } & = 9.46 \times 10^{12} \text{ km} \\ & =9.46 \times 10^{12} \text{ km } \times \frac{1 \text{ Earth diameter}}{12,700 \text{ km}} \\ & =7.45 \times 10^8 \text{ Earth diameters} \end{aligned} \nonumber\]

Isso significa que 1 ano-luz é cerca de 745 milhões de vezes o diâmetro da Terra.

NOMEANDO ESTRELAS

Você pode estar se perguntando por que as estrelas têm uma variedade tão confusa de nomes. Basta olhar para as três primeiras estrelas para medir suas paralaxes: 61 Cygni, Alpha Centauri e Vega. Cada um desses nomes vem de uma tradição diferente de designar estrelas.

As estrelas mais brilhantes têm nomes que derivam dos antigos. Alguns são do grego, como Sirius, que significa “o queimado” — uma referência ao seu brilho. Alguns são do latim, mas muitos dos nomes mais conhecidos vêm do árabe porque, conforme discutido em Observando o céu: o nascimento da astronomia, grande parte da astronomia grega e romana foi “redescoberta” na Europa após a Idade das Trevas por meio de traduções para o árabe. Vega, por exemplo, significa “águia voadora”, e Betelgeuse (pronunciado “suco de besouro”) significa “mão direita da central”.

Em 1603, o astrônomo alemão Johann Bayer (1572-1625) introduziu uma abordagem mais sistemática para nomear estrelas. Para cada constelação, ele atribuiu uma letra grega às estrelas mais brilhantes, aproximadamente em ordem de brilho. Na constelação de Orion, por exemplo, Betelgeuse é a estrela mais brilhante, por isso recebeu a primeira letra do alfabeto grego — alfa — e é conhecida como Alpha Orionis. (“Orionis” é a forma possessiva de Orion, então Alpha Orionis significa “o primeiro de Orion”.) Uma estrela chamada Rigel, sendo a segunda mais brilhante nessa constelação, é chamada de Beta Orionis (Figura\(\PageIndex{4}\)). Como existem 24 letras no alfabeto grego, esse sistema permite a rotulagem de 24 estrelas em cada constelação, mas as constelações têm muito mais estrelas do que isso.

\(\PageIndex{4}\)Objetos de figura em Orion. (a) Esta imagem mostra os objetos mais brilhantes dentro ou perto do padrão estelar de Orion, o caçador (da mitologia grega), na constelação de Orion. (b) Observe as letras gregas do sistema da Bayer neste diagrama da constelação de Orion. Os objetos indicados como M42, M43 e M78 não são estrelas, mas nebulosas — nuvens de gás e poeira; esses números vêm de uma lista de “objetos difusos” feita por Charles Messier em 1781.

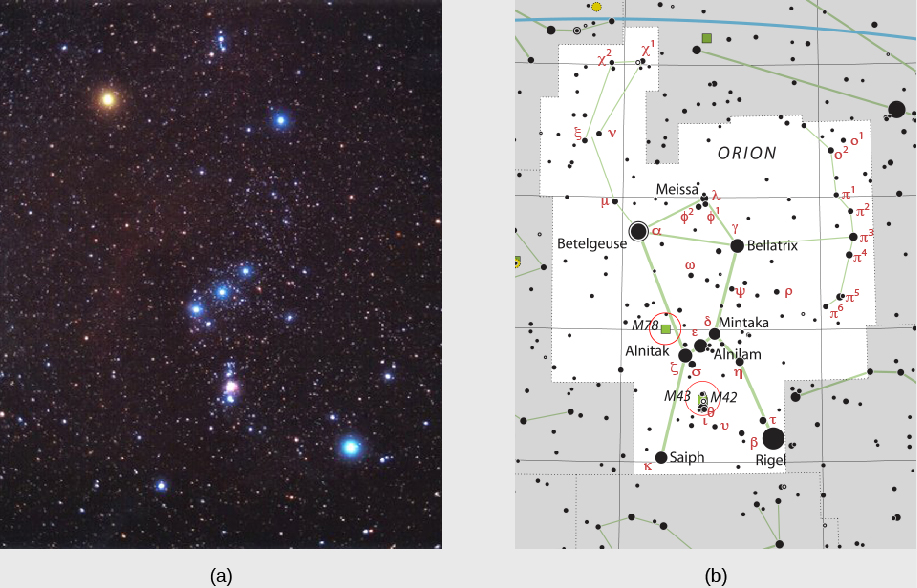
Em 1725, o astrônomo inglês Royal John Flamsteed introduziu outro sistema, no qual as estrelas mais brilhantes eventualmente obtiveram um número em cada constelação em ordem de sua localização no céu ou, mais precisamente, de sua ascensão reta. (O sistema de coordenadas do céu que inclui a ascensão reta foi discutido na Terra, na Lua e no Céu.) Nesse sistema, Betelgeuse é chamada de 58 Orionis e 61 Cygni é a 61ª estrela na constelação de Cygnus, o cisne.

Fica pior. À medida que os astrônomos começaram a entender cada vez mais sobre estrelas, eles elaboraram uma série de catálogos especializados de estrelas, e os fãs desses catálogos começaram a chamar as estrelas pelos números de seus catálogos. Se você olhar o Apêndice I — nossa lista das estrelas mais próximas (muitas das quais são muito fracas para obter um nome antigo, letra Bayer ou número Flamsteed) — você verá referências a alguns desses catálogos. Um exemplo é um conjunto de estrelas rotuladas com um número BD, para “Bonner Durchmusterung”. Este era um catálogo gigantesco de mais de 324.000 estrelas em uma série de zonas no céu, organizado no Observatório de Bonn nas décadas de 1850 e 1860. Lembre-se de que esse catálogo foi feito antes da fotografia ou dos computadores entrarem em uso, então a posição de cada estrela teve que ser medida (pelo menos duas vezes) a olho nu, uma tarefa assustadora.

Há também um sistema completamente diferente para rastrear estrelas cuja luminosidade varia e outro para estrelas que brilham explosivamente em momentos imprevisíveis. Os astrônomos se acostumaram com os diversos sistemas de nomenclatura de estrelas, mas os estudantes geralmente os acham desconcertantes e desejam que os astrônomos optem por um. Não segure a respiração: na astronomia, como em muitos campos do pensamento humano, a tradição tem uma atração poderosa. Ainda assim, com bancos de dados de computadores de alta velocidade para auxiliar a memória humana, os nomes podem se tornar cada vez menos necessários. Os astrônomos de hoje geralmente se referem às estrelas por suas localizações precisas no céu, e não por seus nomes ou vários números de catálogo.

As estrelas mais próximas

Nenhuma estrela conhecida (além do Sol) está dentro de 1 ano-luz ou mesmo 1 parsec da Terra. Os vizinhos estelares mais próximos do Sol são três estrelas na constelação do Centaurus. A olho nu, a mais brilhante dessas três estrelas é Alpha Centauri, que fica a apenas 30○ do polo sul celeste e, portanto, não é visível do continente dos Estados Unidos. A própria Alpha Centauri é uma estrela binária — duas estrelas em revolução mútua — muito próximas umas das outras para serem distinguidas sem um telescópio. Essas duas estrelas estão a 4,4 anos-luz de nós. Perto está uma terceira estrela fraca, conhecida como Proxima Centauri. Proxima, com uma distância de 4,3 anos-luz, está um pouco mais perto de nós do que as outras duas estrelas. Se Proxima Centauri faz parte de um sistema estelar triplo com o binário Alpha Centauri, como parece provável, então seu período orbital pode ser superior a 500.000 anos.

Proxima Centauri é um exemplo do tipo mais comum de estrela e nosso tipo mais comum de vizinho estelar (como vimos em Estrelas: Um Censo Celestial). As anãs M vermelhas de baixa massa compõem cerca de 70% de todas as estrelas e dominam o censo de estrelas dentro de 10 parsecs do Sol. A última pesquisa da vizinhança solar contou 357 estrelas e anãs marrons em 10 parsecs, e 248 delas são anãs vermelhas. No entanto, se você quisesse ver uma anã M a olho nu, você estaria sem sorte. Essas estrelas produzem apenas uma fração da luz solar e quase todas elas precisam de um telescópio para serem detectadas.

A estrela mais próxima visível sem telescópio da maioria dos Estados Unidos é a estrela que aparece mais brilhante de todas as estrelas, Sirius, que tem uma distância de pouco mais de 8 anos-luz. Também é um sistema binário, composto por uma fraca anã branca orbitando uma estrela branco-azulada da sequência principal. É uma interessante coincidência de números que a luz do Sol chegue até nós em cerca de 8 minutos e da próxima estrela mais brilhante do céu em cerca de 8 anos.

Exemplo\(\PageIndex{2}\): Calculando o diâmetro do sol

Para estrelas próximas, podemos medir a aparente mudança em suas posições à medida que a Terra orbita o Sol. Escrevemos anteriormente que um objeto deve estar a 206.265 UA de distância para ter uma paralaxe de um segundo de arco. Isso deve parecer um número muito estranho, mas você pode descobrir por que esse é o valor certo. Começaremos estimando o diâmetro do Sol e depois aplicaremos a mesma ideia a uma estrela com uma paralaxe de 1 segundo de arco. Faça um esboço que tenha um círculo redondo para representar o Sol, coloque a Terra a alguma distância e coloque um observador nela. Desenhe duas linhas a partir do ponto em que o observador está parado, uma em cada lado do Sol. Desenhe um círculo centrado na Terra com sua circunferência passando pelo centro do Sol. Agora pense nas proporções. O Sol se estende cerca de meio grau no céu. Um círculo completo tem 360○. A circunferência do círculo centrado na Terra e passando pelo Sol é dada por:

\[\text{circumference } =2 \pi \times 93,000,000 \text{ miles} \nonumber\]

Então, as duas proporções a seguir são iguais:

\[\frac{0.5^{\circ}}{360^{\circ}} = \frac{\text{diameter of Sun}}{2 \pi \times 93,000,000} \nonumber\]

Calcule o diâmetro do Sol. Como sua resposta se compara ao diâmetro real?

Solução

Para resolver o diâmetro do Sol, podemos avaliar a expressão acima.

\ [\ begin {aligned}\ text {diâmetro do sol} & =\ frac {0,5^ {\ circ}} {360^ {\ circ}}
\ times 2\ pi\ times 93.000.000\ text {miles}\\ =811.577\ text {miles}\ end {aligned}\ nonumber\]

Isso é muito próximo do valor real de cerca de 848.000 milhas.

Exercício\(\PageIndex{2}\)

Agora aplique essa ideia para calcular a distância até uma estrela que tenha uma paralaxe de 1 arcsec. Desenhe uma imagem semelhante à sugerida acima e calcule a distância em AU. (Dica: lembre-se de que o ângulo de paralaxe é definido por 1 UA, não 2 UA, e que 3600 segundos de arco = 1 grau.)

Responda

206.265 AU

Medindo paralaxes no espaço

As medições da paralaxe estelar foram revolucionadas pelo lançamento da espaçonave Hipparcos em 1989, que mediu distâncias de milhares de estrelas até cerca de 300 anos-luz com uma precisão de 10 a 20% (veja a Figura\(\PageIndex{5}\) e o artigo sobre Paralaxe e Astronomia Espacial abaixo). No entanto, até 300 anos-luz têm menos de 1% do tamanho do disco principal do nosso Galaxy.

Em dezembro de 2013, o sucessor de Hipparcos, chamado Gaia, foi lançado pela Agência Espacial Europeia. Gaia está medindo a posição e as distâncias de quase um bilhão de estrelas com uma precisão de alguns milionésimos de um segundo de arco. O limite de distância de Gaia se estenderá muito além de Hiparcos, estudando estrelas até 30.000 anos-luz (100 vezes mais longe do que Hiparcos, cobrindo quase 1/3 do disco galáctico). Gaia também será capaz de medir os movimentos adequados ² para milhares de estrelas no halo da Via Láctea, algo que só pode ser feito para as estrelas mais brilhantes no momento. No final da missão de Gaia, não teremos apenas um mapa tridimensional de uma grande fração de nossa própria Via Láctea, mas também teremos um forte elo na cadeia de distâncias cósmicas que estamos discutindo neste capítulo. No entanto, para estender essa cadeia além do alcance de Gaia e explorar distâncias até galáxias próximas, precisamos de algumas técnicas completamente novas.

Figura Diagrama\(\PageIndex{5}\) H—R de estrelas medido por Gaia e Hiparcos. Este gráfico inclui 16.631 estrelas para as quais as paralaxes têm uma precisão de 10% ou mais. As cores indicam o número de estrelas em cada ponto do diagrama, com o vermelho correspondendo ao maior número e o azul ao menor. A luminosidade é plotada ao longo do eixo vertical, com a luminosidade aumentando para cima. Uma cor infravermelha é plotada como um proxy da temperatura, com a temperatura diminuindo para a direita. A maioria dos pontos de dados é distribuída ao longo da diagonal que vai do canto superior esquerdo (alta luminosidade, alta temperatura) até o canto inferior direito (baixa temperatura, baixa luminosidade). Essas são as estrelas da sequência principal. O grande conjunto de pontos de dados acima da sequência principal no lado direito do diagrama é composto por estrelas gigantes vermelhas.

paralaxe e astronomia espacial

Uma das coisas mais difíceis de medir com precisão os pequenos ângulos das mudanças de paralaxe da Terra é que você tem que observar as estrelas através da atmosfera do nosso planeta. Como vimos em Instrumentos Astronômicos, o efeito da atmosfera é espalhar os pontos de luz das estrelas em discos difusos, dificultando as medições exatas de suas posições. Os astrônomos há muito sonhavam em ser capazes de medir paralaxes do espaço, e dois observatórios em órbita agora transformaram esse sonho em realidade.

O nome do satélite Hipparcos, lançado em 1989 pela Agência Espacial Europeia, é ao mesmo tempo uma abreviatura de High Precision Parallax Collecting Satellite e uma homenagem a Hipparchus, o astrônomo grego pioneiro cujo trabalho discutimos em Observando o Céu: O Nascimento da Astronomia. O satélite foi projetado para fazer as medições de paralaxe mais precisas da história, a 36.000 quilômetros acima da Terra. No entanto, seu motor de foguete a bordo não disparou, o que significa que ele não recebeu o impulso necessário para atingir a altitude desejada. Hipparcos acabou passando sua vida útil de 4 anos em uma órbita elíptica que variou de 500 a 36.000 quilômetros de altura. Nessa órbita, o satélite mergulhava nos cinturões de radiação da Terra a cada 5 horas ou mais, o que finalmente afetou os painéis solares que forneciam energia para alimentar os instrumentos.

No entanto, a missão foi bem-sucedida, resultando em dois catálogos. Um dá posições de 120.000 estrelas com uma precisão de um milésimo de segundo de arco — aproximadamente o diâmetro de uma bola de golfe em Nova York vista da Europa. O segundo catálogo contém informações de mais de um milhão de estrelas, cujas posições foram medidas em trinta milésimos de um segundo de arco. Agora temos medições precisas de paralaxe de estrelas em distâncias de cerca de 300 anos-luz. (Com telescópios terrestres, medições precisas eram viáveis em apenas cerca de 60 anos-luz.)

Para aproveitar o sucesso de Hipparcos, em 2013, a Agência Espacial Europeia lançou um novo satélite chamado Gaia. A missão Gaia está programada para durar 5 anos. Como Gaia carrega telescópios maiores do que Hipparcos, ela pode observar estrelas mais fracas e medir suas posições 200 vezes mais precisamente. O objetivo principal da missão Gaia é criar um mapa tridimensional preciso dessa parte da galáxia em cerca de 30.000 anos-luz, observando 1 bilhão de estrelas 70 vezes cada, medindo suas posições e, portanto, suas paralaxes e seu brilho.

Por muito tempo, a medição de paralaxes e posições estelares precisas foi um remanso da pesquisa astronômica, principalmente porque a precisão das medições não melhorou muito por cerca de 100 anos. No entanto, a capacidade de fazer medições a partir do espaço revolucionou esse campo da astronomia e continuará a fornecer um elo crítico em nossa cadeia de distâncias cósmicas.

A Agência Espacial Europeia (ESA) mantém um site da missão Gaia, onde você pode aprender mais sobre a missão Gaia e obter as últimas notícias sobre as observações de Gaia.

Para saber mais sobre Hipparcos, explore esta página da Agência Espacial Europeia com um podcast da ESA Charting the Galaxy, de Hipparcos a Gaia.

Resumo

Para estrelas que estão relativamente próximas, podemos “triangular” as distâncias de uma linha de base criada pelo movimento anual da Terra em torno do Sol. Metade da mudança na posição de uma estrela próxima em relação a estrelas de fundo muito distantes, vista de lados opostos da órbita da Terra, é chamada de paralaxe dessa estrela e é uma medida de sua distância. As unidades usadas para medir a distância estelar são o ano-luz, a distância que a luz percorre em 1 ano e o parsec (pc), a distância de uma estrela com paralaxe de 1 arco-segundo (1 parsec = 3,26 anos-luz). A estrela mais próxima, uma anã vermelha, está a mais de 1 parsec de distância. As primeiras medições bem-sucedidas de paralaxes estelares foram relatadas em 1838. As medições de paralaxe são um elo fundamental na cadeia de distâncias cósmicas. O satélite Hipparcos nos permitiu medir paralaxes precisos para estrelas em cerca de 300 anos-luz, e a missão Gaia resultará em paralaxes de até 30.000 anos-luz.

Notas de pé

¹ Para ter alguma base de comparação, o planeta anão Plutão orbita a uma distância média de 40 UA do Sol, e o planeta anão Eris está atualmente a aproximadamente 96 UA do Sol.

² O movimento adequado (conforme discutido em Analisando a luz das estrelas) é o movimento de uma estrela no céu (perpendicular à nossa linha de visão).

Glossário

paralaxe

um aparente deslocamento de uma estrela próxima que resulta do movimento da Terra ao redor do Sol

parsec

uma unidade de distância em astronomia, igual a 3,26 anos-luz; a uma distância de 1 parsec, uma estrela tem uma paralaxe de 1 arco-segundo