5.6: O efeito Doppler
- Page ID
- 183546
Objetivos de
Ao final desta seção, você poderá:
- Explique por que as linhas espectrais dos fótons que observamos de um objeto mudarão como resultado do movimento do objeto em nossa direção ou para longe de nós
- Descreva como podemos usar o efeito Doppler para deduzir como objetos astronômicos estão se movendo no espaço
As duas últimas seções apresentaram muitos conceitos novos, e esperamos que, por meio deles, você tenha visto surgir uma grande ideia. Os astrônomos podem aprender sobre os elementos em estrelas e galáxias decodificando as informações em suas linhas espectrais. No entanto, há um fator complicador em aprender a decodificar a mensagem da luz das estrelas. Se uma estrela estiver se aproximando ou se afastando de nós, suas linhas estarão em um lugar ligeiramente diferente no espectro de onde elas estariam em uma estrela em repouso. E a maioria dos objetos no universo tem algum movimento em relação ao Sol.
O movimento afeta as ondas
Em 1842, Christian Doppler mediu pela primeira vez o efeito do movimento nas ondas contratando um grupo de músicos para tocar em um vagão aberto enquanto ele se movia pela pista. Ele então aplicou o que aprendeu a todas as ondas, incluindo a luz, e ressaltou que, se uma fonte de luz estiver se aproximando ou se afastando do observador, as ondas de luz serão, respectivamente, mais amontoadas ou espalhadas. O princípio geral, agora conhecido como efeito Doppler, é ilustrado na Figura\(\PageIndex{1}\).
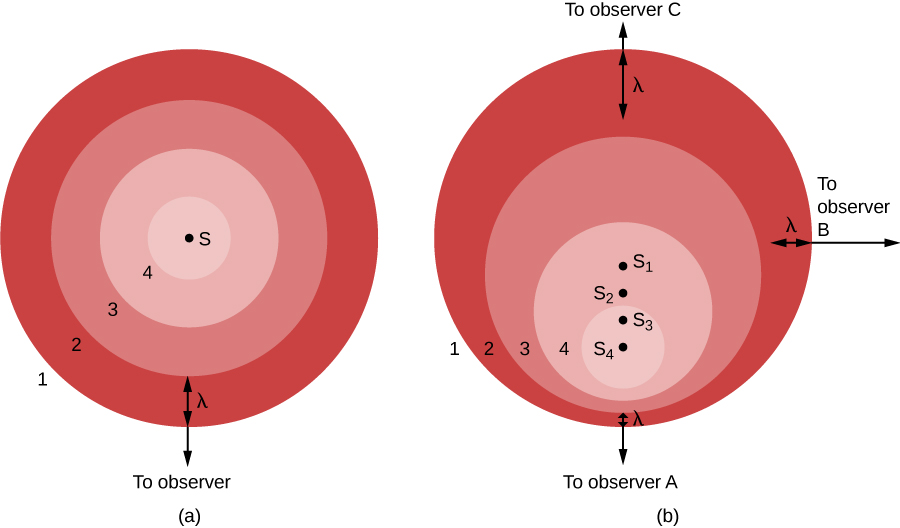
Na Figura\(\PageIndex{1a}\), a fonte de luz (S) está em repouso em relação ao observador. A fonte emite uma série de ondas, cujas cristas chamamos de 1, 2, 3 e 4. As ondas de luz se espalham uniformemente em todas as direções, como as ondulações de um respingo em um lago. As cristas são separadas por uma distância, λ, onde λ é o comprimento de onda. O observador, que por acaso está localizado na direção da parte inferior da imagem, vê as ondas de luz se aproximando de maneira agradável e uniforme, com um comprimento de onda de distância. Observadores localizados em qualquer outro lugar veriam a mesma coisa.
Por outro lado, se a fonte de luz estiver se movendo em relação ao observador, como visto na Figura\(\PageIndex{1b}\), a situação é mais complicada. Entre o momento em que uma crista é emitida e a próxima está pronta para sair, a fonte se moveu um pouco, em direção à parte inferior da página. Do ponto de vista do observador A, esse movimento da fonte diminuiu a distância entre as cristas — está comprimindo as cristas, diria esse observador.
Na Figura\(\PageIndex{1b}\), mostramos a situação da perspectiva de três observadores. A fonte é vista em quatro posições,\(S_1\),\(S_2\), e\(S_3\)\(S_4\), cada uma correspondendo à emissão de uma crista de onda. Para o observador A, as ondas parecem se seguir mais de perto, em um comprimento de onda diminuído e, portanto, maior frequência. (Lembre-se de que todas as ondas de luz viajam à velocidade da luz pelo espaço vazio, não importa o que aconteça. Isso significa que o movimento não pode afetar a velocidade, mas apenas o comprimento de onda e a frequência. Conforme o comprimento de onda diminui, a frequência deve aumentar. Se as ondas forem mais curtas, mais poderão se mover a cada segundo.)
A situação não é a mesma para outros observadores. Vejamos a situação do ponto de vista do observador C, localizado em frente ao observador A na Figura\(\PageIndex{1}\). Para ela, a fonte está se afastando de sua localização. Como resultado, as ondas não são comprimidas, mas sim espalhadas pelo movimento da fonte. As cristas chegam com um comprimento de onda aumentado e uma frequência diminuída. Para observar B, em uma direção perpendicular ao movimento da fonte, nenhum efeito é observado. O comprimento de onda e a frequência permanecem os mesmos da parte (a) da figura.
Podemos ver nesta ilustração que o efeito Doppler é produzido somente por um movimento em direção ou afastamento do observador, um movimento chamado velocidade radial. O movimento lateral não produz esse efeito. Observadores entre A e B observariam algum encurtamento das ondas de luz na parte do movimento da fonte que está ao longo de sua linha de visão. Observadores entre B e C observariam o alongamento das ondas de luz que estão ao longo de sua linha de visão.
Você pode ter ouvido o efeito Doppler com ondas sonoras. Quando um apito de trem ou sirene policial se aproxima de você e depois se afasta, você notará uma diminuição no tom (que é como os sentidos humanos interpretam a frequência das ondas sonoras) das ondas sonoras. Em comparação com as ondas em repouso, elas mudaram de um pouco mais frequentes quando se aproximam de você para um pouco menos frequentes ao se afastar de você.
Um bom exemplo dessa mudança no som do apito de um trem pode ser ouvido no final da clássica música dos Beach Boys “Caroline, No” em seu álbum Pet Sounds. Para ouvir esse som, acesse esta versão da música no YouTube. O som do trem começa aproximadamente às 2:20.
Mudanças de cor
Quando a fonte das ondas se move em sua direção, o comprimento de onda diminui um pouco. Se as ondas envolvidas forem luz visível, as cores da luz mudarão ligeiramente. À medida que o comprimento de onda diminui, eles se deslocam em direção à extremidade azul do espectro: os astrônomos chamam isso de desvio para o azul (já que o final do espectro é realmente violeta, o termo provavelmente deveria ser desvio violeta, mas azul é uma cor mais comum). Quando a fonte se afasta de você e o comprimento de onda fica maior, chamamos a mudança nas cores de desvio para o vermelho. Como o efeito Doppler foi usado pela primeira vez com a luz visível na astronomia, os termos “desvio para o azul” e “desvio para o vermelho” se tornaram bem estabelecidos. Hoje, os astrônomos usam essas palavras para descrever as mudanças nos comprimentos de onda das ondas de rádio ou raios X de forma tão confortável quanto as usam para descrever mudanças na luz visível.
Quanto maior for o movimento em direção ou para longe de nós, maior será o desvio do Doppler. Se o movimento relativo estiver inteiramente ao longo da linha de visão, a fórmula para o desvio de luz do Doppler é
\[\dfrac{\Delta λ}{λ}= \frac{v}{c} \nonumber\]
onde\(\lambda\) é o comprimento de onda emitido pela fonte,\(\Delta \lambda\) é a diferença entre\(\lambda\) e o comprimento de onda medido pelo observador,\(c\) é a velocidade da luz e\(v\) é a velocidade relativa do observador e da fonte na linha de visão. A variável\(v\) é contada como positiva se a velocidade for de recessão e negativa se for de aproximação. Resolvendo essa equação para a velocidade, encontramos
\[ v = c \times \dfrac{\Delta \lambda}{\lambda}. \nonumber\]
Se uma estrela se aproxima ou se afasta de nós, os comprimentos de onda da luz em seu espectro contínuo parecem encurtados ou alongados, respectivamente, assim como os das linhas escuras. No entanto, a menos que sua velocidade seja de dezenas de milhares de quilômetros por segundo, a estrela não parece visivelmente mais azul ou vermelha do que o normal. Portanto, o desvio do Doppler não é facilmente detectado em um espectro contínuo e não pode ser medido com precisão nesse espectro. No entanto, os comprimentos de onda das linhas de absorção podem ser medidos com precisão e seu desvio de Doppler é relativamente simples de detectar.
Exemplo\(\PageIndex{1}\): O efeito Doppler
Podemos usar a equação do efeito Doppler para calcular a velocidade radial de um objeto se soubermos três coisas: a velocidade da luz, o comprimento de onda original (não deslocado) da luz emitida e a diferença entre o comprimento de onda da luz emitida e o comprimento de onda que observamos. Para linhas específicas de absorção ou emissão, geralmente sabemos exatamente qual comprimento de onda a linha tem em nossos laboratórios na Terra, onde a fonte de luz não está se movendo. Podemos medir o novo comprimento de onda com nossos instrumentos no telescópio e, portanto, sabemos a diferença no comprimento de onda devido ao deslocamento do Doppler. Como a velocidade da luz é uma constante universal, podemos então calcular a velocidade radial da estrela.
Uma linha de emissão específica de hidrogênio é originalmente emitida com um comprimento de onda de 656,3 nm de uma nuvem de gás. Em nosso telescópio, observamos que o comprimento de onda da linha de emissão é de 656,6 nm. Com que rapidez essa nuvem de gás está se movendo em direção ou se afastando da Terra?
Solução
Como a luz é deslocada para um comprimento de onda maior (desvio para o vermelho), sabemos que essa nuvem de gás está se afastando de nós. A velocidade pode ser calculada usando a fórmula de desvio Doppler:
\[ν=c×\dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left( \dfrac{0.3 ~ \text{nm}}{656.3 ~ \text{nm}} \right)= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.3 \times 10^{–9} ~ \text{m}}{656.3 \times 10^{–9} ~ \text{m}} \right)=140,000 ~ \text{m/s} =140 ~ \text{km/s} \nonumber\]
Exercício\(\PageIndex{1}\)
Suponha que uma linha espectral de hidrogênio, normalmente a 500 nm, seja observada no espectro de uma estrela em 500,1 nm. A que velocidade a estrela está se movendo em direção ou se afastando da Terra?
- Responda
-
Como a luz é deslocada para um comprimento de onda maior, a estrela está se afastando de nós:
\[ν=c \times \dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 ~ \text{nm}}{500 ~ \text{nm}} \right)=\left( 3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 \times 10^{–9} ~ \text{m}}{500 \times 10^{–9} ~ \text{m}} \right)=60,000 ~ \text{m/s}\]
Sua velocidade é de 60.000 m/s.
Agora você pode estar se perguntando: se todas as estrelas estiverem se movendo e o movimento mudar o comprimento de onda de cada linha espectral, isso não será um desastre para os astrônomos tentando descobrir quais elementos estão presentes nas estrelas? Afinal, é o comprimento de onda (ou cor) preciso que diz aos astrônomos quais linhas pertencem a qual elemento. E primeiro medimos esses comprimentos de onda em recipientes de gás em nossos laboratórios, que não estão se movendo. Se cada linha no espectro de uma estrela agora é deslocada por seu movimento para um comprimento de onda (cor) diferente, como podemos ter certeza de quais linhas e quais elementos estamos vendo em uma estrela cuja velocidade não conhecemos?
Tenha coragem. Essa situação parece pior do que realmente é. Os astrônomos raramente julgam a presença de um elemento em um objeto astronômico por uma única linha. É o padrão de linhas exclusivo do hidrogênio ou do cálcio que nos permite determinar se esses elementos fazem parte da estrela ou galáxia que estamos observando. O efeito Doppler não altera o padrão das linhas de um determinado elemento — ele apenas desloca o padrão inteiro levemente em direção a comprimentos de onda mais vermelhos ou azuis. O padrão alterado ainda é muito fácil de reconhecer. O melhor de tudo é que, quando reconhecemos o padrão de um elemento familiar, recebemos um bônus: a quantidade em que o padrão é alterado pode nos permitir determinar a velocidade dos objetos em nossa linha de visão.
O treinamento de astrônomos inclui muito trabalho para aprender a decodificar a luz (e outras radiações eletromagnéticas). Um “decodificador” habilidoso pode aprender a temperatura de uma estrela, quais elementos estão nela e até mesmo sua velocidade em uma direção em nossa direção ou longe de nós. Essa é realmente uma quantidade impressionante de informações para estrelas que estão a anos-luz de distância.
Resumo
Se um átomo está se movendo em nossa direção quando um elétron muda de órbita e produz uma linha espectral, vemos essa linha se deslocar levemente em direção ao azul de seu comprimento de onda normal em um espectro. Se o átomo estiver se afastando, vemos a linha deslocada em direção ao vermelho. Esse deslocamento é conhecido como efeito Doppler e pode ser usado para medir as velocidades radiais de objetos distantes.
Glossário
- Efeito Doppler
- a aparente mudança no comprimento de onda ou na frequência da radiação de uma fonte devido ao seu movimento relativo para longe ou em direção ao observador
- velocidade radial
- movimento em direção ou afastamento do observador; o componente da velocidade relativa que está na linha de visão


