13.6: Teorema binomial
- Page ID
- 186585
- Aplique o Teorema Binomial.
Um polinômio com dois termos é chamado de binômio. Já aprendemos a multiplicar binômios e a transformar binômios em potências, mas elevar um binômio a uma alta potência pode ser entediante e demorado. Nesta seção, discutiremos um atalho que nos permitirá encontrar\((x+y)^n\) sem multiplicar o binômio por si só\(n\).
Identificação de coeficientes binomiais
No atalho para encontrar\({(x+y)}^n\), precisaremos usar combinações para encontrar os coeficientes que aparecerão na expansão do binômio. Nesse caso, usamos a notação\(\dbinom{n}{r}\) em vez de\(C(n,r)\), mas ela pode ser calculada da mesma forma. Então
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!}\]
A combinação\(\dbinom{n}{r}\) é chamada de coeficiente binomial. Um exemplo de coeficiente binomial é:
\(\dbinom{5}{2}=C(5,2)=10\)
Se\(n\) e\(r\) forem números inteiros maiores ou iguais a\(0\) com\(n≥r\), então o coeficiente binomial é
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!} \label{binomial1}\]
Sim. Assim como o número de combinações deve ser sempre um número inteiro, um coeficiente binomial sempre será um número inteiro.
Encontre cada coeficiente binomial.
- \(\dbinom{5}{3}\)
- \(\dbinom{9}{2}\)
- \(\dbinom{9}{7}\)
Solução
Use a Equação\ ref {binomial1} para calcular cada coeficiente binomial. Você também pode usar a\(nC_r\) função na sua calculadora.
- \(\dbinom{5}{3}=\dfrac{5!}{3!(5−3)!}=\dfrac{5⋅4⋅3!}{3!2!}=10\)
- \(\dbinom{9}{2}=\dfrac{9!}{2!(9−2)!}=\dfrac{9⋅8⋅7!}{2!7!}=36\)
- \(\dbinom{9}{7}=\dfrac{9!}{7!(9−7)!}=\dfrac{9⋅8⋅7!}{7!2!}=36\)
Análise
Observe que obtivemos o mesmo resultado para as partes (b) e (c). Se você observar atentamente a solução para essas duas partes, verá que acaba com os mesmos dois fatoriais no denominador, mas a ordem é invertida, assim como acontece com as combinações.
\[\dbinom{n}{r}=\dbinom{n}{n−r} \nonumber\]
Encontre cada coeficiente binomial.
- \(\dbinom{7}{3}\)
- \(\dbinom{11}{4}\)
- Responda a
-
\(35\)
- Resposta b
-
\(33\)
Usando o Teorema Binomial
Quando expandimos\({(x+y)}^n\) multiplicando, o resultado é chamado de expansão binomial e inclui coeficientes binomiais. Se quiséssemos expandir\({(x+y)}^{52}\), poderíamos multiplicar\((x+y)\) por si só cinquenta e duas vezes. Isso pode levar horas! Se examinarmos algumas expansões binomiais simples, podemos encontrar padrões que nos levarão a um atalho para encontrar expansões binomiais mais complicadas.
\[\begin{align*} {(x+y)}^2 &= x^2+2xy+y^2 \\[4pt] {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\[4pt] {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Primeiro, vamos examinar os expoentes. Com cada termo sucessivo, o expoente para\(x\) diminui e o expoente para\(y\) aumentos. A soma dos dois expoentes é\(n\) para cada termo.
Em seguida, vamos examinar os coeficientes. Observe que os coeficientes aumentam e depois diminuem em um padrão simétrico. Os coeficientes seguem um padrão:
\(\dbinom{n}{0}\),\(\dbinom{n}{1}\)\(\dbinom{n}{2}\),...,\(\dbinom{n}{n}.\)
Esses padrões nos levam ao Teorema Binomial, que pode ser usado para expandir qualquer binômio.
\[\begin{align*} {(x+y)}^n&=\sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k \\[4pt] &=x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \end{align*}\]
Outra forma de ver os coeficientes é examinar a expansão de um binômio na forma geral,\(x+y\), para potências sucessivas\(1\)\(2\)\(3\),,\(4\) e.
\[\begin{align*} {(x+y)}^1 &= x+y \\ {(x+y)}^2 &= x^2+2xy+y^2 \\ {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\ {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Você consegue adivinhar a próxima expansão para o binômio\({(x+y)}^5\)?

Figura\(\PageIndex{1}\)
Veja a Figura\(\PageIndex{1}\), que ilustra o seguinte:
- Existem\(n+1\) termos na expansão do\({(x+y)}^n\).
- O grau (ou soma dos expoentes) para cada termo é\(n\).
- Os poderes ativados\(x\) começam com\(n\) e diminuem para\(0\).
- Os poderes ativados\(y\) começam com\(0\) e aumentam para\(n\).
- Os coeficientes são simétricos.
Para determinar a expansão em\({(x+y)}^5\), vemos\(n=5\), portanto, que haverá\(5+1=6\) termos. Cada termo tem um grau combinado de\(5\). Em ordem decrescente para as potências de\(x\), o padrão é o seguinte:
- Introduza e\(x^5\), em seguida, para cada termo sucessivo, reduza o expoente em\(x\)\(1\) até que\(x^0=1\) seja alcançado.
- Introduza e\(y^0=1\), em seguida, aumente o expoente em yy em 1 até que\(y^5\) seja alcançado.
\(x^5, x^4y, x^3y^2, x^2y^3, xy^4, y^5\)
A próxima expansão seria
\({(x+y)}^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5\)
Mas de onde vêm esses coeficientes? Os coeficientes binomiais são simétricos. Podemos ver esses coeficientes em uma matriz conhecida como Triângulo de Pascal, mostrada na Figura\(\PageIndex{2}\).
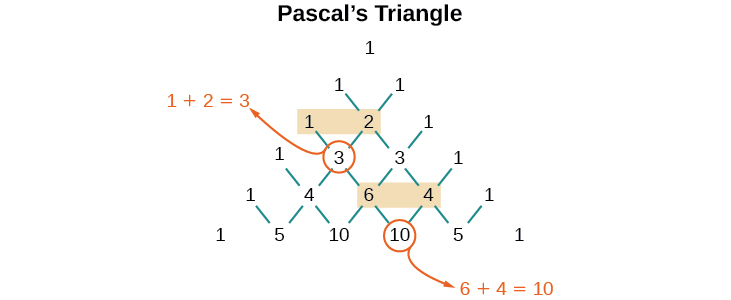
Figura\(\PageIndex{2}\)
Para gerar o Triângulo de Pascal, começamos escrevendo um\(1\). Na linha abaixo, linha 2, escrevemos dois\(1’s\). Na 3ª linha, flanqueie as extremidades das linhas com\(1’s\) e adicione\(1+1\) para encontrar o número do meio\(2\). Na\(n^{th}\) fileira, flanqueie as extremidades da linha com\(1’s\). Cada elemento no triângulo é a soma dos dois elementos imediatamente acima dele.
Para ver a conexão entre o Triângulo de Pascal e os coeficientes binomiais, vamos revisitar a expansão dos binômios na forma geral.
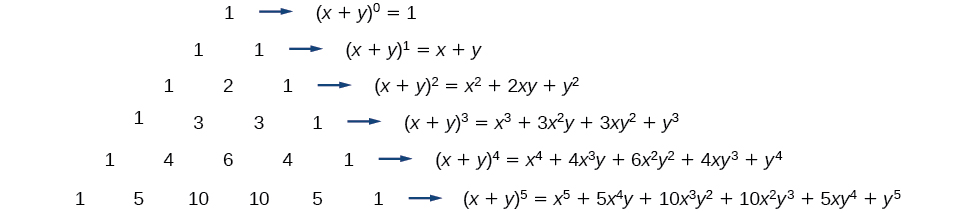
O Teorema Binomial é uma fórmula que pode ser usada para expandir qualquer binômio.
\[ {(x+y)}^n = \sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k = x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \]
- Determine o valor de de\(n\) acordo com o expoente.
- \(k=0\)Avalie o\(k=n\) usando a fórmula do Teorema Binomial.
- Simplifique.
Escreva em formato expandido.
- \({(x+y)}^5\)
- \({(3x−y)}^4\)
Solução
a. Substitua\(n=5\) na fórmula. Avalie\(k=0\) os\(k=5\) termos de entrega. Simplifique.
\[\begin{align*} {(x+y)}^5 &= \dbinom{5}{0}x^5y^0+\dbinom{5}{1}x^4y^1+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}x^1y^4+\dbinom{5}{5}x^0y^5 \\ {(x+y)}^5 &= x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5 \end{align*}\]
b. Substitua\(n=4\) na fórmula. Avalie\(k=0\) os\(k=4\) termos de entrega. Observe que\(3x\) está no lugar que foi ocupado por\(x\) e que\(–y\) está no lugar que foi ocupado por\(y\). Então, nós os substituímos. Simplifique.
\[\begin{align*} {(3x−y)}^4 &= \dbinom{4}{0}{(3x)}^4{(−y)}^0+\dbinom{4}{1}{(3x)}^3{(−y)}^1+\dbinom{4}{2}{(3x)}^2{(−y)}^2+\dbinom{4}{3}{(3x)}^1{(−y)}^3+\dbinom{4}{4}{(3x)}^0{(−y)}^4 \\ {(3x−y)}^4 &= 81x^4−108x^3y+54x^2y^2−12xy^3+y^4 \end{align*}\]
Análise
Observe os sinais alternados na parte b. Isso acontece porque\((−y)\) elevado a potências ímpares é negativo, mas\((−y)\) elevado a potências pares é positivo. Isso ocorrerá sempre que o binômio contiver um sinal de subtração.
Escreva em formato expandido.
- \({(x−y)}^5\)
- \({(2x+5y)}^3\)
- Responda a
-
\(x^5−5x^4y+10x^3y^2−10x^2y^3+5xy^4−y^5\)
- Resposta b
-
\(8x^3+60x^2y+150xy^2+125y^3\)
Usando o teorema binomial para encontrar um único termo
Expandir um binômio com um alto expoente, como\({(x+2y)}^{16}\) pode ser um processo demorado. Às vezes, estamos interessados apenas em um determinado termo de expansão binomial. Não precisamos expandir totalmente um binômio para encontrar um único termo específico.
Observe o padrão dos coeficientes na expansão de\({(x+y)}^5\).
\({(x+y)}^5=x^5+\dbinom{5}{1}x^4y+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}xy^4+y^5\)
O segundo termo é\(\dbinom{5}{1}x^4y\). O terceiro termo é\(\dbinom{5}{2}x^3y^2\). Podemos generalizar esse resultado.
O\((r+1)\) décimo termo da expansão binomial de\({(x+y)}^n\) é:
\[\dbinom{n}{r}x^{n−r}y^r \label{binomial5}\]
- Determine o valor de nn de acordo com o expoente.
- Determinar\((r+1)\).
- Determinar\(r\).
- Substitua\(r\) na fórmula\((r+1)\) o termo da expansão binomial.
Encontre o décimo termo de\({(x+2y)}^{16}\) sem expandir totalmente o binômio.
Solução
Como estamos procurando o décimo termo\(r+1=10\), usaremos\(r=9\) em nossos cálculos e a Equação\ ref {binomial5}.
\(\dbinom{16}{9}x^{16−9}{(2y)}^9=5,857,280x^7y^9\)
Encontre o sexto termo de\({(3x−y)}^9\) sem expandir totalmente o binômio.
- Responda
-
\(−10,206x^4y^5\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com expansão binomial.
Equações-chave
| Teorema binomial | \({(x+y)}^n=\sum_{k=0}^n\dbinom{n}{k}x^{n−k}y^k\) |
| \((r+1)\)o termo de uma expansão binomial | \(\dbinom{n}{r}x^{n−r}y^r\) |
Key Concepts
- \(\dbinom{n}{r}\) is called a binomial coefficient and is equal to \(C(n,r)\). See Example \(\PageIndex{1}\).
- The Binomial Theorem allows us to expand binomials without multiplying. See Example \(\PageIndex{2}\).
- We can find a given term of a binomial expansion without fully expanding the binomial. See Example \(\PageIndex{3}\).


