13.2: Sequências aritméticas
- Page ID
- 186607
- Encontre a diferença comum para uma sequência aritmética.
- Escreva termos de uma sequência aritmética.
- Use uma fórmula recursiva para uma sequência aritmética.
- Use uma fórmula explícita para uma sequência aritmética.
As empresas geralmente fazem grandes compras, como computadores e veículos, para uso comercial. O valor contábil desses suprimentos diminui a cada ano para fins fiscais. Essa diminuição no valor é chamada de depreciação. Um método de cálculo da depreciação é a depreciação linear, na qual o valor do ativo diminui na mesma quantia a cada ano.
Como exemplo, considere uma mulher que inicia um pequeno negócio de contratação. Ela compra um caminhão novo para\($25,000\). Depois de cinco anos, ela estima que poderá vender o caminhão por\($8,000\). A perda de valor do caminhão será, portanto, de\($17,000\),\($3,400\) por ano, durante cinco anos. O caminhão valerá\($21,600\) após o primeiro ano;\($18,200\) depois de dois anos;\($14,800\) depois de três anos;\($11,400\) depois de quatro anos; e\($8,000\) no final de cinco anos. Nesta seção, consideraremos tipos específicos de sequências que nos permitirão calcular a depreciação, como o valor do caminhão.
Encontrando diferenças comuns
Diz-se que os valores do caminhão no exemplo formam uma sequência aritmética porque eles mudam em uma quantidade constante a cada ano. Cada termo aumenta ou diminui pelo mesmo valor constante chamado de diferença comum da sequência. Para essa sequência, a diferença comum é\(-3,400\).

A sequência abaixo é outro exemplo de uma sequência aritmética. Nesse caso, a diferença constante é\(3\). Você pode escolher qualquer termo da sequência e adicionar\(3\) para encontrar o termo subsequente.

Uma sequência aritmética é uma sequência que tem a propriedade de que a diferença entre quaisquer dois termos consecutivos é uma constante. Essa constante é chamada de diferença comum. Se\(a_1\) for o primeiro termo de uma sequência aritmética e\(d\) for a diferença comum, a sequência será:
\[\{a_n\}=\{a_1,a_1+d,a_1+2d,a_1+3d,...\}\]
Cada sequência é aritmética? Em caso afirmativo, encontre a diferença comum.
- \(\{1,2,4,8,16,...\}\)
- \(\{−3,1,5,9,13,...\}\)
Solução
Subtraia cada termo do termo subsequente para determinar se existe uma diferença comum.
- A sequência não é aritmética porque não há nenhuma diferença comum.
\(2-1={\color{red}1} \qquad 4-2={\color{red}2} \qquad 8-4={\color{red}4} \qquad 16-8={\color{red}8}\)
- A sequência é aritmética porque há uma diferença comum. A diferença comum é\(4\).
\(1-(-3)={\color{red}4} \qquad 5-1={\color{red}4} \qquad 9-5={\color{red}4} \qquad 13-9={\color{red}4}\)
Análise
O gráfico de cada uma dessas sequências é mostrado na Figura\(\PageIndex{1}\). Podemos ver nos gráficos que, embora ambas as sequências mostrem crescimento, (a) não é linear, enquanto (b) é linear. As sequências aritméticas têm uma taxa de mudança constante, então seus gráficos sempre serão pontos em uma linha.
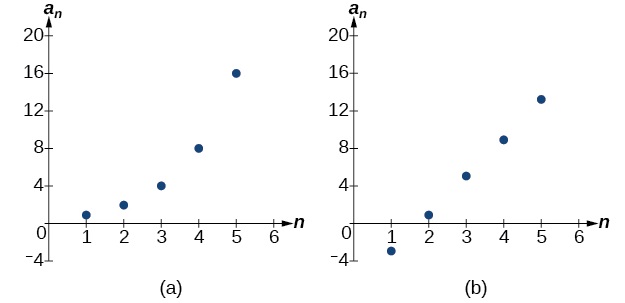
Figura\(\PageIndex{1}\)
Se nos disserem que uma sequência é aritmética, temos que subtrair cada termo do termo seguinte para encontrar a diferença comum?
Não. Se soubermos que a sequência é aritmética, podemos escolher qualquer termo na sequência e subtraí-lo do termo subsequente para encontrar a diferença comum.
A sequência dada é aritmética? Em caso afirmativo, encontre a diferença comum.
\(\{18, 16, 14, 12, 10,…\}\)
- Responda
-
A sequência é aritmética. A diferença comum é\(–2\).
A sequência dada é aritmética? Em caso afirmativo, encontre a diferença comum.
\(\{1, 3, 6, 10, 15,…\}\)
- Responda
-
A sequência não é aritmética porque\(3−1≠6−3\).
Escrevendo termos de sequências aritméticas
Agora que podemos reconhecer uma sequência aritmética, encontraremos os termos se recebermos o primeiro termo e a diferença comum. Os termos podem ser encontrados começando com o primeiro termo e adicionando a diferença comum repetidamente. Além disso, qualquer termo também pode ser encontrado inserindo os valores de\(n\) e\(d\) na fórmula abaixo.
\[a_n=a_1+(n−1)d\]
- Adicione a diferença comum ao primeiro termo para encontrar o segundo termo.
- Adicione a diferença comum ao segundo termo para encontrar o terceiro termo.
- Continue até que todos os termos desejados sejam identificados.
- Escreva os termos separados por vírgulas entre colchetes.
Escreva os primeiros cinco termos da sequência aritmética com\(a_1=17\)\(d=−3\) e.
Solução
Adicionar\(−3\) é o mesmo que subtrair\(3\). Começando com o primeiro termo, subtraia\(3\) de cada termo para encontrar o próximo termo.
Os primeiros cinco termos são\(\{17,14,11,8,5\}\)
Análise
Como esperado, o gráfico da sequência consiste em pontos em uma linha, conforme mostrado na Figura\(\PageIndex{2}\).
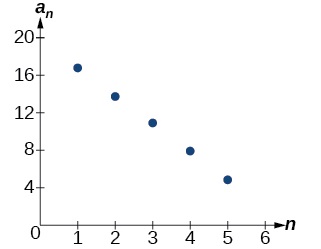
Figura\(\PageIndex{2}\)
Liste os primeiros cinco termos da sequência aritmética com\(a_1=1\)\(d=5\) e.
- Responda
-
\(\{1, 6, 11, 16, 21\}\)
- Substitua os valores dados para\(a_1\),\(a_n\),\(n\) na fórmula\(a_n=a_1+(n−1)d\) a ser resolvida\(d\).
- Encontre um determinado termo substituindo os valores apropriados para\(a_1\)\(n\), e\(d\) na fórmula\(a_n=a_1+(n−1)d\).
Dado\(a_1=8\) e\(a_4=14\), encontre\(a_5\).
Solução
A sequência pode ser escrita em termos do termo inicial\(8\) e da diferença comum\(d\).
\(\{8,8+d,8+2d,8+3d\}\)
Sabemos que o quarto termo é igual\(14\); sabemos que o quarto termo tem a forma\(a_1+3d=8+3d\).
Podemos encontrar a diferença comum\(d\).
\[\begin{align*} a_n&= a_1+(n-1)d \\ a_4&= a_1+3d \\ a_4&=8+3d\qquad \text{Write the fourth term of the sequence in terms of }a_1 \text{ and } d. \\ 14&=8+3d\qquad \text{Substitute }14 \text{ for } a_4. \\ d&=2\qquad \text{Solve for the common difference.} \end{align*}\]
Encontre o quinto termo adicionando a diferença comum ao quarto termo.
\(a_5=a_4+2=16\)
Análise
Observe que a diferença comum é adicionada ao primeiro termo uma vez para encontrar o segundo termo, duas vezes para encontrar o terceiro termo, três vezes para encontrar o quarto termo e assim por diante. O décimo termo pode ser encontrado adicionando a diferença comum ao primeiro termo nove vezes ou usando a equação\(a_n=a_1+(n−1)d\).
Dado\(a_3=7\) e\(a_5=17\), encontre\(a_2\).
- Responda
-
\(a_2=2\)
Usando fórmulas recursivas para sequências aritméticas
Algumas sequências aritméticas são definidas em termos do termo anterior usando uma fórmula recursiva. A fórmula fornece uma regra algébrica para determinar os termos da sequência. Uma fórmula recursiva nos permite encontrar qualquer termo de uma sequência aritmética usando uma função do termo anterior. Cada termo é a soma do termo anterior e da diferença comum. Por exemplo, se a diferença comum for\(5\), então cada termo é o termo anterior mais\(5\). Como acontece com qualquer fórmula recursiva, o primeiro termo deve ser dado.
\(a_n=a_n−1+d\)
para\(n≥2\)
A fórmula recursiva para uma sequência aritmética com diferença comum\(d\) é:
\[a_n=a_n−1+d\]
para\(n≥2\)
- Subtraia qualquer termo do termo subsequente para encontrar a diferença comum.
- Declare o termo inicial e substitua a diferença comum na fórmula recursiva para sequências aritméticas.
Escreva uma fórmula recursiva para a sequência aritmética.
\(\{−18, −7, 4, 15, 26, …\}\)
Solução
O primeiro termo é dado como\(−18\). A diferença comum pode ser encontrada subtraindo o primeiro termo do segundo termo.
\(d=−7−(−18)=11\)
Substitua o termo inicial e a diferença comum na fórmula recursiva para sequências aritméticas.
\(a_1=−18\)
\(a_n=a_{n−1}+11\)
para\(n≥2\)
Análise
Vemos que a diferença comum é a inclinação da linha formada quando representamos graficamente os termos da sequência, conforme mostrado na Figura\(\PageIndex{3}\). O padrão de crescimento da sequência mostra a diferença constante de 11 unidades.
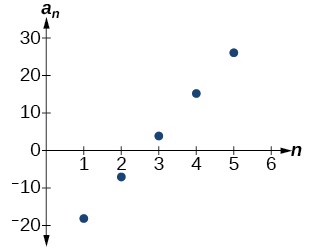
Figura\(\PageIndex{3}\)
Precisamos subtrair o primeiro termo do segundo termo para encontrar a diferença comum?
Não. Podemos subtrair qualquer termo na sequência do termo subsequente. No entanto, é mais comum subtrair o primeiro termo do segundo, porque geralmente é o método mais fácil de encontrar a diferença comum.
Escreva uma fórmula recursiva para a sequência aritmética.
\(\{25, 37, 49, 61, …\}\)
- Responda
-
\(\begin{align*}a_1 &= 25 \\ a_n &= a_{n−1}+12 , \text{ for }n≥2 \end{align*}\)
Usando fórmulas explícitas para sequências aritméticas
Podemos pensar em uma sequência aritmética como uma função no domínio dos números naturais; é uma função linear porque tem uma taxa de variação constante. A diferença comum é a taxa constante de mudança ou a inclinação da função. Podemos construir a função linear se soubermos a inclinação e a interceptação vertical.
\(a_n=a_1+d(n−1)\)
Para encontrar o\(y\) intercepto -da função, podemos subtrair a diferença comum do primeiro termo da sequência. Considere a seguinte sequência.

A diferença comum é que\(−50\), portanto, a sequência representa uma função linear com uma inclinação de\(−50\). Para encontrar o\(y\) intercepto -, subtraímos\(−50\) de\(200\):\(200−(−50)=200+50=250\). Você também pode encontrar o\(y\) intercepto -representando graficamente a função e determinando onde uma linha que conecta os pontos cruzaria o eixo vertical. O gráfico é mostrado na Figura\(\PageIndex{4}\).
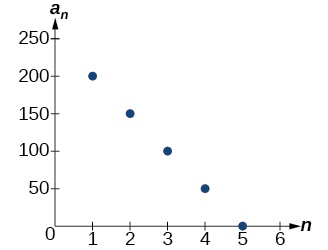
Figura\(\PageIndex{4}\)
Lembre-se de que a forma de interceptação de inclinação de uma linha é\(y=mx+b\). Ao lidar com sequências, usamos\(a_n\) no lugar de\(y\) e\(n\) no lugar de\(x\). Se soubermos a inclinação e a interceptação vertical da função, podemos substituí-las por\(m\) e\(b\) na forma de interceptação de inclinação de uma linha. Substituindo\(−50\) a inclinação e\(250\) a interceptação vertical, obtemos a seguinte equação:
\(a_n=−50n+250\)
Não precisamos encontrar o intercepto vertical para escrever uma fórmula explícita para uma sequência aritmética. Outra fórmula explícita para essa sequência é\(a_n=200−50(n−1)\), que simplifica para\(a_n=−50n+250\).
Uma fórmula explícita para o\(n^{th}\) termo de uma sequência aritmética é dada por
\[a_n=a_1+d(n−1)\]
- Encontre a diferença comum,\(a_2−a_1\).
- Substitua a diferença comum e o primeiro termo em\(a_n=a_1+d(n−1)\).
Escreva uma fórmula explícita para a sequência aritmética.
\(\{2, 12, 22, 32, 42, …\}\)
Solução
A diferença comum pode ser encontrada subtraindo o primeiro termo do segundo termo.
\[\begin{align*} d &= a_2−a_1 \\ &= 12−2 \\ &= 10 \end{align*}\]
A diferença comum é\(10\). Substitua a diferença comum e o primeiro termo da sequência na fórmula e simplifique.
\[\begin{align*}a_n &= 2+10(n−1) \\ a_n &= 10n−8 \end{align*}\]
Análise
O gráfico dessa sequência, representado na Figura\(\PageIndex{5}\), mostra uma inclinação\(10\) e uma interceptação vertical de\(−8\).

Figura\(\PageIndex{5}\)
Escreva uma fórmula explícita para a seguinte sequência aritmética.
\(\{50,47,44,41,…\}\)
- Responda
-
\(a_n=53−3n\)
Encontrando o número de termos em uma sequência aritmética finita
Fórmulas explícitas podem ser usadas para determinar o número de termos em uma sequência aritmética finita. Precisamos encontrar a diferença comum e, em seguida, determinar quantas vezes a diferença comum deve ser adicionada ao primeiro termo para obter o termo final da sequência.
- Descubra a diferença comum\(d\).
- Substitua a diferença comum e o primeiro termo em\(a_n=a_1+d(n–1)\).
- Substitua o último termo por\(a_n\) e resolva por\(n\).
Encontre o número de termos na sequência aritmética finita.
\(\{8, 1, –6, ..., –41\}\)
Solução
A diferença comum pode ser encontrada subtraindo o primeiro termo do segundo termo.
\(1−8=−7\)
A diferença comum é\(−7\). Substitua a diferença comum e o termo inicial da sequência na fórmula do enésimo termo e simplifique.
\[\begin{align*} a_n &= a_1+d(n−1) \\ a_n &= 8+−7(n−1) \\ a_n &= 15−7n \end{align*}\]
\(−41\)Substitua\(a_n\) e resolva\(n\)
\[\begin{align*} -41&=15-7n\\ 8&=n \end{align*}\]
Há oito termos na sequência.
Encontre o número de termos na sequência aritmética finita.
\(\{6, 11, 16, ..., 56\}\)
- Responda
-
Há\(11\) termos na sequência.
Resolvendo problemas de aplicação com sequências aritméticas
Em muitos problemas de aplicação, geralmente faz sentido usar um termo inicial de\(a_0\) em vez de\(a_1\). Nesses problemas, alteramos ligeiramente a fórmula explícita para levar em conta a diferença nos termos iniciais. Usamos a seguinte fórmula:
\[a_n=a_0+dn\]
Uma criança de cinco anos recebe um subsídio por\($1\) semana. Seus pais prometem a ele um aumento anual de\($2\) por semana.
- Escreva uma fórmula para o subsídio semanal da criança em um determinado ano.
- Qual será o subsídio da criança quando ela tiver\(16\) anos de idade?
Solução
- A situação pode ser modelada por uma sequência aritmética com um termo inicial de\(1\) e uma diferença comum de\(2\).
\(A\)Seja o valor do subsídio e\(n\) o número de anos após a idade\(5\). Usando a fórmula explícita alterada para uma sequência aritmética, obtemos:
\(A_n=1+2n\)
- Podemos encontrar o número de anos desde a idade\(5\) subtraindo.
\(16−5=11\)
Estamos procurando o subsídio para crianças depois de\(11\) anos. Substitua\(11\) na fórmula para encontrar o subsídio da criança por idade\(16\).
\(A_{11}=1+2(11)=23\)
O subsídio para crianças na idade\(16\) será\($23\) por semana.
Uma mulher decide fazer uma corrida de 5\(10\) minutos todos os dias desta semana e planeja aumentar o tempo de sua corrida diária em\(4\) minutos a cada semana. Escreva uma fórmula para o tempo de sua corrida após\(n\) semanas. Quanto tempo sua corrida diária durará\(8\) semanas a partir de hoje?
- Responda
-
A fórmula é\(T_n=10+4n\), e ela levará\(42\) minutos.
Acesse este recurso on-line para obter instruções e práticas adicionais com sequências aritméticas.
Equações-chave
| fórmula recursiva para o enésimo termo de uma sequência aritmética | \(a_n=a_{n−1}+d\)\(n≥2\) |
| fórmula explícita para o enésimo termo de uma sequência aritmética | \(a_n=a_1+d(n−1)\) |
Key Concepts
- An arithmetic sequence is a sequence where the difference between any two consecutive terms is a constant.
- The constant between two consecutive terms is called the common difference.
- The common difference is the number added to any one term of an arithmetic sequence that generates the subsequent term. See Example \(\PageIndex{1}\).
- The terms of an arithmetic sequence can be found by beginning with the initial term and adding the common difference repeatedly. See Example \(\PageIndex{2}\) and Example \(\PageIndex{3}\).
- A recursive formula for an arithmetic sequence with common difference dd is given by \(a_n=a_{n−1}+d\), \(n≥2\). See Example \(\PageIndex{4}\).
- As with any recursive formula, the initial term of the sequence must be given.
- An explicit formula for an arithmetic sequence with common difference \(d\) is given by \(a_n=a_1+d(n−1)\). See Example \(\PageIndex{5}\).
- An explicit formula can be used to find the number of terms in a sequence. See Example \(\PageIndex{6}\).
- In application problems, we sometimes alter the explicit formula slightly to \(a_n=a_0+dn\). See Example \(\PageIndex{7}\).


