12.2: A hipérbole

Objetivos de

• Localize os vértices e focos de uma hipérbole.
• Escreva equações de hipérboles na forma padrão.
• Faça um gráfico de hipérboles centradas na origem.
• Faça um gráfico de hipérboles não centradas na origem.
• Resolva problemas aplicados envolvendo hipérboles.

O que caminhos de cometas, estrondos supersônicos, antigos pilares gregos e torres de resfriamento de tiragem natural têm em comum? Todos eles podem ser modelados pelo mesmo tipo de cônica. Por exemplo, quando algo se move mais rápido do que a velocidade do som, uma onda de choque na forma de um cone é criada. Uma parte de uma cônica é formada quando a onda cruza o solo, resultando em um estrondo sônico (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): Uma onda de choque que cruza o solo forma uma parte de uma cônica e resulta em um estrondo sônico.

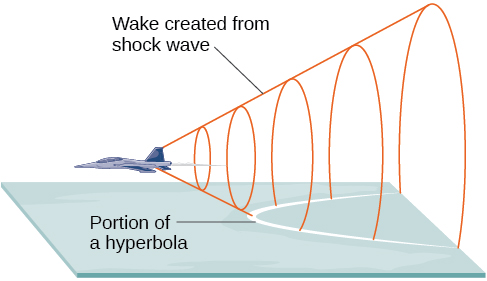
A maioria das pessoas está familiarizada com o boom sônico criado por aeronaves supersônicas, mas os humanos estavam quebrando a barreira do som muito antes do primeiro voo supersônico. O estalo de um chicote ocorre porque a ponta está excedendo a velocidade do som. As balas disparadas por muitas armas de fogo também quebram a barreira do som, embora o estrondo da arma geralmente substitua o som do estrondo sônico.

Localizando os vértices e focos de uma hipérbole

Em geometria analítica, uma hipérbole é uma seção cônica formada pela interseção de um cone circular reto com um plano em um ângulo de forma que ambas as metades do cone sejam cruzadas. Essa interseção produz duas curvas separadas e ilimitadas que são imagens espelhadas uma da outra (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Uma hipérbole

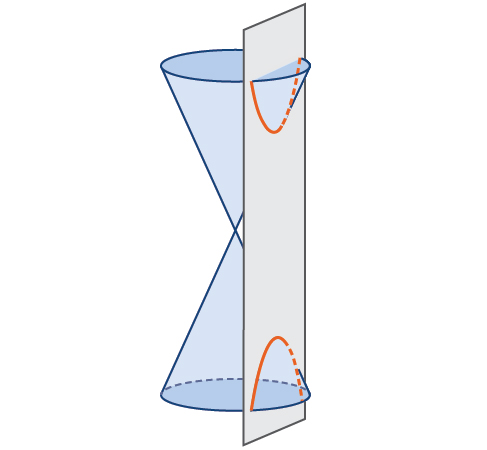
Como a elipse, a hipérbole também pode ser definida como um conjunto de pontos no plano coordenado. Uma hipérbole é o conjunto de todos os pontos\((x,y)\) em um plano, de forma que a diferença das distâncias entre\((x,y)\) e os focos seja uma constante positiva.

Observe que a definição de uma hipérbole é muito semelhante à de uma elipse. A diferença é que a hipérbole é definida em termos da diferença de duas distâncias, enquanto a elipse é definida em termos da soma de duas distâncias.

Assim como na elipse, cada hipérbole tem dois eixos de simetria. O eixo transversal é um segmento de linha que passa pelo centro da hipérbole e tem vértices como pontos finais. Os focos estão na linha que contém o eixo transversal. O eixo conjugado é perpendicular ao eixo transversal e tem os co-vértices como suas extremidades. O centro de uma hipérbole é o ponto médio dos eixos transversal e conjugado, onde eles se cruzam. Cada hipérbole também tem duas assíntotas que passam pelo seu centro. Quando uma hipérbole se afasta do centro, seus galhos se aproximam dessas assíntotas. O retângulo central da hipérbole está centrado na origem com lados que passam por cada vértice e co-vértice; é uma ferramenta útil para representar graficamente a hipérbole e suas assíntotas. Para esboçar as assíntotas da hipérbole, basta esboçar e estender as diagonais do retângulo central (Figura\(\PageIndex{3}\)).

Figura\(\PageIndex{3}\): Principais características da hipérbole

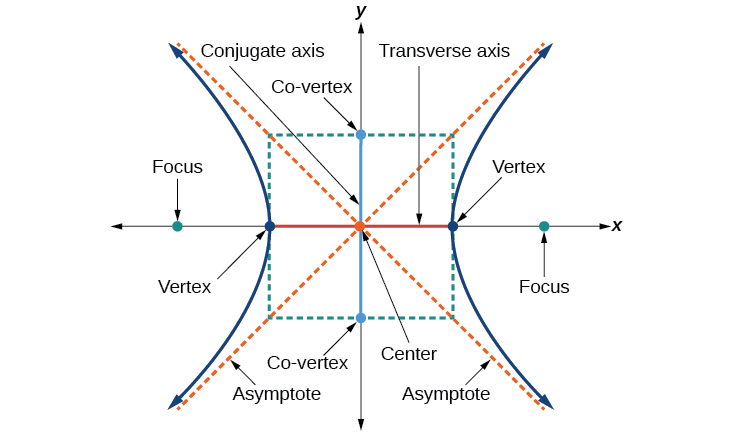
Nesta seção, limitaremos nossa discussão às hipérboles que estão posicionadas vertical ou horizontalmente no plano coordenado; os eixos ficarão sobre ou ficarão paralelos aos\(y\) eixos\(x\) - e. Vamos considerar dois casos: aqueles que estão centrados na origem e aqueles que estão centrados em um ponto diferente da origem.

Derivando a equação de uma elipse centrada na origem

Seja\((−c,0)\) e\((c,0)\) seja o foco de uma hipérbole centrada na origem. A hipérbole é o conjunto de todos os pontos\((x,y)\), de forma que a diferença entre as\((x,y)\) distâncias e os focos seja constante. Veja a Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\)

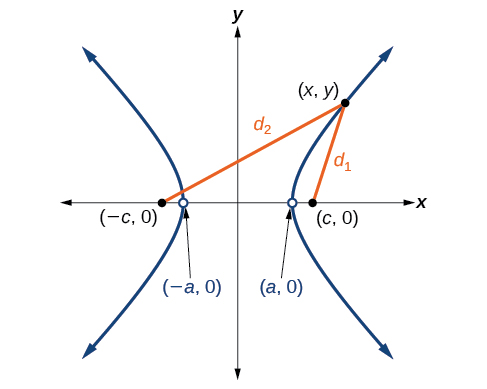
Se\((a,0)\) for um vértice da hipérbole, a distância de\((−c,0)\) até\((a,0)\) é\(a−(−c)=a+c\). A distância de\((c,0)\) para\((a,0)\) é\(c−a\). A soma das distâncias dos focos ao vértice é

\((a+c)−(c−a)=2a\)

Se\((x,y)\) for um ponto na hipérbole, podemos definir as seguintes variáveis:

\(d_2=\)a distância de\((−c,0)\) até\((x,y)\)

\(d_1=\)a distância de\((c,0)\) até\((x,y)\)

Por definição de hipérbole,\(d_2−d_1\) é constante para qualquer ponto\((x,y)\) da hipérbole. Sabemos que a diferença dessas distâncias é\(2a\) para o vértice\((a,0)\). Isso se segue\(d_2−d_1=2a\) para qualquer ponto da hipérbole. Assim como na derivação da equação de uma elipse, começaremos aplicando a fórmula da distância. O resto da derivação é algébrica. Compare essa derivação com a da seção anterior para elipses.

\[\begin{align*} d_2-d_1&=2a\\ \sqrt{{(x-(-c))}^2+{(y-0)}^2}-\sqrt{{(x-c)}^2+{(y-0)}^2}&=2a\qquad \text{Distance Formula}\\ \sqrt{{(x+c)}^2+y^2}-\sqrt{{(x-c)}^2+y^2}&=2a\qquad \text{Simplify expressions.}\\ \sqrt{{(x+c)}^2+y^2}&=2a+\sqrt{{(x-c)}^2+y^2}\qquad \text{Move radical to opposite side.}\\ {(x+c)}^2+y^2&={(2a+\sqrt{{(x-c)}^2+y^2})}^2\qquad \text{Square both sides.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+{(x-c)}^2+y^2\qquad \text{Expand the squares.}\\ x^2+2cx+c^2+y^2&=4a^2+4a\sqrt{{(x-c)}^2+y^2}+x^2-2cx+c^2+y^2\qquad \text{Expand remaining square.}\\ 2cx&=4a^2+4a\sqrt{{(x-c)}^2+y^2}-2cx\qquad \text{Combine like terms.}\\ 4cx-4a^2&=4a\sqrt{{(x-c)}^2+y^2}\qquad \text{Isolate the radical.}\\ cx-a^2&=a\sqrt{{(x-c)}^2+y^2}\qquad \text{Divide by 4.}\\ {(cx-a^2)}^2&=a^2{\left[\sqrt{{(x-c)}^2+y^2}\right]}^2\qquad \text{Square both sides.}\\ c^2x^2-2a^2cx+a^4&=a^2(x^2-2cx+c^2+y^2)\qquad \text{Expand the squares.}\\ c^2x^2-2a^2cx+a^4&=a^2x^2-2a^2cx+a^2c^2+a^2y^2\qquad \text{Distribute } a^2\\ a^4+c^2x^2&=a^2x^2+a^2c^2+a^2y^2\qquad \text{Combine like terms.}\\ c^2x^2-a^2x^2-a^2y^2&=a^2c^2-a^4\qquad \text{Rearrange terms.}\\ x^2(c^2-a^2)-a^2y^2&=a^2(c^2-a^2)\qquad \text{Factor common terms.}\\ x^2b^2-a^2y^2&=a^2b^2\qquad \text{Set } b^2=c^2−a^2\\. \dfrac{x^2b^2}{a^2b^2}-\dfrac{a^2y^2}{a^2b^2}&=\dfrac{a^2b^2}{a^2b^2}\qquad \text{Divide both sides by } a^2b^2\\ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\\ \end{align*}\]

Essa equação define uma hipérbole centrada na origem com vértices\((\pm a,0)\) e co-vértices\((0,\pm b)\).

FORMAS PADRÃO DA EQUAÇÃO DE UMA HIPÉRBOLE COM CENTRO\((0,0)\)

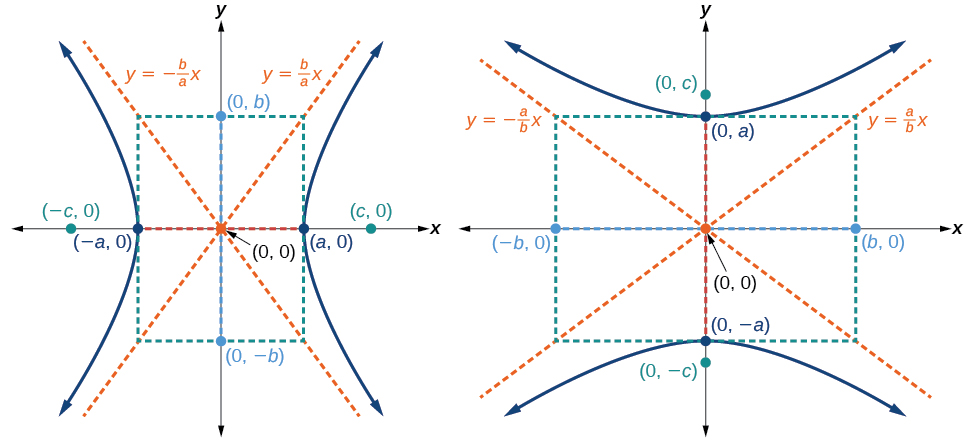
A forma padrão da equação de uma hipérbole com eixo central\((0,0)\) e transversal no\(x\) eixo -é

\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)

onde

• o comprimento do eixo transversal é\(2a\)
• as coordenadas dos vértices são\((\pm a,0)\)
• o comprimento do eixo conjugado é\(2b\)
• as coordenadas dos co-vértices são\((0,\pm b)\)
• a distância entre os focos é\(2c\), onde\(c^2=a^2+b^2\)
• as coordenadas dos focos são\((\pm c,0)\)
• as equações das assíntotas são\(y=\pm \dfrac{b}{a}x\)

Veja a Figura\(\PageIndex{5a}\).

A forma padrão da equação de uma hipérbole com eixo central\((0,0)\) e transversal no\(y\) eixo -é

\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)

onde

• o comprimento do eixo transversal é\(2a\)
• as coordenadas dos vértices são\((0,\pm a)\)
• o comprimento do eixo conjugado é\(2b\)
• as coordenadas dos co-vértices são\((\pm b,0)\)
• a distância entre os focos é\(2c\), onde\(c^2=a^2+b^2\)
• as coordenadas dos focos são\((0,\pm c)\)
• as equações das assíntotas são\(y=\pm \dfrac{a}{b}x\)

Veja a Figura\(\PageIndex{5b}\).

Observe que os vértices, co-vértices e focos estão relacionados pela equação\(c^2=a^2+b^2\). Quando recebemos a equação de uma hipérbole, podemos usar essa relação para identificar seus vértices e focos.

Figura\(\PageIndex{5}\): (a) Hipérbole horizontal com centro\((0,0)\) (b) Hipérbole vertical com centro\((0,0)\)

Como: Dada a equação de uma hipérbole na forma padrão, localize seus vértices e focos

1. Determine se o eixo transversal está no\(y\) eixo\(x\) - ou -. Observe que\(a^2\) está sempre abaixo da variável com o coeficiente positivo. Então, se você definir a outra variável igual a zero, poderá encontrar facilmente as interceptações. No caso em que a hipérbole está centrada na origem, as interceptações coincidem com os vértices.
   • Se a equação tiver a forma\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), o eixo transversal estará no\(x\) eixo y. Os vértices estão localizados em\((\pm a,0)\), e os focos estão localizados em\((\pm c,0)\).
   • Se a equação tiver a forma\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), o eixo transversal estará no\(y\) eixo y. Os vértices estão localizados em\((0,\pm a)\), e os focos estão localizados em\((0,\pm c)\).
2. Resolva o\(a\) uso da equação\(a=\sqrt{a^2}\).
3. Resolva o\(c\) uso da equação\(c=\sqrt{a^2+b^2}\).

Exemplo\(\PageIndex{1}\): Locating a Hyperbola’s Vertices and Foci

Identifique os vértices e focos da hipérbole com a equação\(\dfrac{y^2}{49}−\dfrac{x^2}{32}=1\).

Solução

A equação tem a forma\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), então o eixo transversal está no\(y\) eixo -. A hipérbole está centrada na origem, então os vértices servem como interceptos y do gráfico. Para encontrar os vértices\(x=0\), defina e resolva para\(y\).

\[\begin{align*} 1&=\dfrac{y^2}{49}-\dfrac{x^2}{32}\\ 1&=\dfrac{y^2}{49}-\dfrac{0^2}{32}\\ 1&=\dfrac{y^2}{49}\\ y^2&=49\\ y&=\pm \sqrt{49}\\ &=\pm 7 \end{align*}\]

Os focos estão localizados em\((0,\pm c)\). Resolvendo para\(c\),

\[\begin{align*} c&=\sqrt{a^2+b^2}\\ &=\sqrt{49+32}\\ &=\sqrt{81}\\ &=9 \end{align*}\]

Portanto, os vértices estão localizados em\((0,\pm 7)\) e os focos estão localizados em\((0,9)\).

Exercício\(\PageIndex{1}\)

Identifique os vértices e focos da hipérbole com a equação\(\dfrac{x^2}{9}−\dfrac{y^2}{25}=1\).

Responda

Vértices:\((\pm 3,0)\); Focos:\((\pm \sqrt{34},0)\)

Escrevendo equações de hipérboles na forma padrão

Assim como nas elipses, escrever a equação de uma hipérbole na forma padrão nos permite calcular as principais características: seu centro, vértices, co-vértices, focos, assíntotas e os comprimentos e posições dos eixos transversal e conjugado. Por outro lado, uma equação para uma hipérbole pode ser encontrada devido às suas principais características. Começamos encontrando equações padrão para hipérboles centradas na origem. Em seguida, voltaremos nossa atenção para encontrar equações padrão para hipérboles centradas em algum ponto diferente da origem.

Hipérboles centradas na origem

Analisando as formas padrão dadas para hipérboles centradas em\((0,0)\), vemos que os vértices, co-vértices e focos estão relacionados pela equação\(c^2=a^2+b^2\). Observe que essa equação também pode ser reescrita como\(b^2=c^2−a^2\). Essa relação é usada para escrever a equação de uma hipérbole quando dadas as coordenadas de seus focos e vértices.

Como: Dados os vértices e focos de uma hipérbole centrada em\((0,0)\), write its equation in standard form

1. Determine se o eixo transversal está no\(y\) eixo\(x\) - ou -.
   • Se as coordenadas dadas dos vértices e focos tiverem a forma\((\pm a,0)\) e\((\pm c,0)\), respectivamente, o eixo transversal será o\(x\) eixo -. Use o formulário padrão\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).
   • Se as coordenadas dadas dos vértices e focos tiverem a forma\((0,\pm a)\) e\((0,\pm c)\), respectivamente, o eixo transversal será o\(y\) eixo -. Use o formulário padrão\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\).
2. Encontre\(b^2\) usando a equação\(b^2=c^2−a^2\).
3. Substitua os valores por\(a^2\) e\(b^2\) na forma padrão da equação determinada na Etapa 1.

Exemplo\(\PageIndex{2}\): Finding the Equation of a Hyperbola Centered at \((0,0)\) Given its Foci and Vertices

Qual é a equação de forma padrão da hipérbole que tem vértices\((\pm 6,0)\) e focos\((\pm 2\sqrt{10},0)\)?

Solução

Os vértices e focos estão no\(x\) eixo y. Assim, a equação da hipérbole terá a forma\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\).

Os vértices são\((\pm 6,0)\), então\(a=6\)\(a^2=36\) e.

Os focos são\((\pm 2\sqrt{10},0)\), então\(c=2\sqrt{10}\)\(c^2=40\) e.

Resolvendo para\(b^2\), temos

\[\begin{align*} b^2&=c^2-a^2\\ b^2&=40-36\qquad \text{Substitute for } c^2 \text{ and } a^2\\ b^2&=4\qquad \text{Subtract.} \end{align*}\]

Finalmente, substituímos\(a^2=36\) e\(b^2=4\) na forma padrão da equação,\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\). A equação da hipérbole é\(\dfrac{x^2}{36}−\dfrac{y^2}{4}=1\), conforme mostrado na Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\)

Exercício\(\PageIndex{2}\)

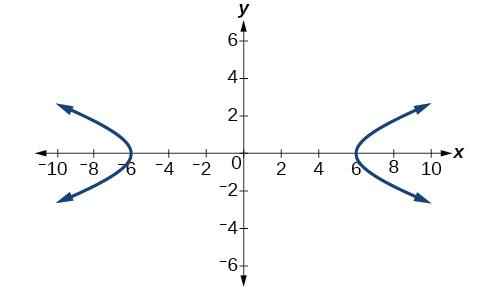
Qual é a equação de forma padrão da hipérbole que tem vértices\((0,\pm 2)\) e focos\((0,\pm 2\sqrt{5})\)?

Responda

\(\dfrac{y^2}{4}−\dfrac{x^2}{16}=1\)

Hipérboles não centradas na origem

Como os gráficos de outras equações, o gráfico de uma hipérbole pode ser traduzido. Se uma hipérbole for traduzida em\(h\) unidades horizontalmente e\(k\) unidades verticalmente, o centro da hipérbole será\((h,k)\). Essa tradução resulta na forma padrão da equação que vimos anteriormente,\(x\) substituída por\((x−h)\) e\(y\) substituída por\((y−k)\).

FORMAS PADRÃO DA EQUAÇÃO DE UMA HIPÉRBOLE COM CENTRO\((H, K)\)

A forma padrão da equação de uma hipérbole com eixo central\((h,k)\) e transversal paralelos ao\(x\) eixo -é

\[\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\]

onde

• o comprimento do eixo transversal é\(2a\)
• as coordenadas dos vértices são\((h\pm a,k)\)
• o comprimento do eixo conjugado é\(2b\)
• as coordenadas dos co-vértices são\((h,k\pm b)\)
• a distância entre os focos é\(2c\), onde\(c^2=a^2+b^2\)
• as coordenadas dos focos são\((h\pm c,k)\)

As assíntotas da hipérbole coincidem com as diagonais do retângulo central. O comprimento do retângulo é\(2a\) e sua largura é\(2b\). As inclinações das diagonais são\(\pm \dfrac{b}{a}\), e cada diagonal passa pelo centro\((h,k)\). Usando a fórmula de inclinação de pontos, é simples mostrar que as equações das assíntotas são\(y=\pm \dfrac{b}{a}(x−h)+k\). Veja a Figura\(\PageIndex{7a}\).

A forma padrão da equação de uma hipérbole com eixo central\((h,k)\) e transversal paralelos ao\(y\) eixo -é

\[\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\]

onde

• o comprimento do eixo transversal é\(2a\)
• as coordenadas dos vértices são\((h,k\pm a)\)
• o comprimento do eixo conjugado é\(2b\)
• as coordenadas dos co-vértices são\((h\pm b,k)\)
• a distância entre os focos é\(2c\), onde\(c^2=a^2+b^2\)
• as coordenadas dos focos são\((h,k\pm c)\)

Usando o raciocínio acima, as equações das assíntotas são\(y=\pm \dfrac{a}{b}(x−h)+k\). Veja a Figura\(\PageIndex{7b}\).

Figura\(\PageIndex{7}\): (a) Hipérbole horizontal com centro\((h,k)\) (b) Hipérbole vertical com centro\((h,k)\)

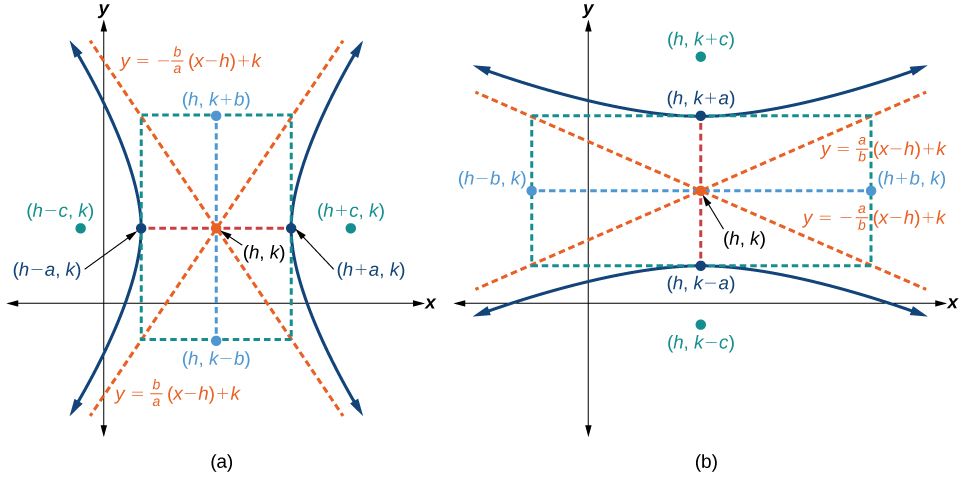
Como as hipérboles centradas na origem, as hipérboles centradas em um ponto\((h,k)\) têm vértices, co-vértices e focos relacionados pela equação\(c^2=a^2+b^2\). Podemos usar essa relação junto com as fórmulas do ponto médio e da distância para encontrar a equação padrão de uma hipérbole quando os vértices e focos são fornecidos.

Como: Dados os vértices e focos de uma hipérbole centrada em\((h,k)\),write its equation in standard form

1. Determine se o eixo transversal é paralelo ao\(y\) eixo\(x\) - ou -.
   • Se as\(y\) coordenadas -dos vértices e focos fornecidos forem as mesmas, então o eixo transversal é paralelo ao\(x\) eixo -. Use o formulário padrão\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\).
   • Se as\(x\) coordenadas -dos vértices e focos fornecidos forem as mesmas, então o eixo transversal é paralelo ao\(y\) eixo -. Use o formulário padrão\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\).
2. Identifique o centro da hipérbole\((h,k)\), usando a fórmula do ponto médio e as coordenadas dadas para os vértices.
3. Encontre\(a^2\) resolvendo o comprimento do eixo transversal,\(2a\), que é a distância entre os vértices fornecidos.
4. Encontre\(c^2\) usando\(h\) e\(k\) encontrado na Etapa 2 junto com as coordenadas fornecidas para os focos.
5. Resolva o\(b^2\) uso da equação\(b^2=c^2−a^2\).
6. Substitua os valores por\(h\)\(k\)\(a^2\),, e\(b^2\) na forma padrão da equação determinada na Etapa 1.

Exemplo\(\PageIndex{3}\): Finding the Equation of a Hyperbola Centered at \((h, k)\) Given its Foci and Vertices

Qual é a equação da forma padrão da hipérbole que tem vértices em\((0,−2)\)\((6,−2)\) e e focos em\((−2,−2)\) e\((8,−2)\)?

Solução

As\(y\) coordenadas -dos vértices e focos são as mesmas, então o eixo transversal é paralelo ao\(x\) eixo -. Assim, a equação da hipérbole terá a forma

\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)

Primeiro, identificamos o centro,\((h,k)\). O centro está a meio caminho entre os vértices\((0,−2)\)\((6,−2)\) e. Aplicando a fórmula do ponto médio, temos

\((h,k)=(\dfrac{0+6}{2},\dfrac{−2+(−2)}{2})=(3,−2)\)

Em seguida, encontramos\(a^2\). O comprimento do eixo transversal,\(2a\), é limitado pelos vértices. Então, podemos encontrar\(a^2\) encontrando a distância entre as\(x\) coordenadas -dos vértices.

\[\begin{align*} 2a&=| 0-6 |\\ 2a&=6\\ a&=3\\ a^2&=9 \end{align*}\]

Agora precisamos encontrar\(c^2\). As coordenadas dos focos são\((h\pm c,k)\). Então\((h−c,k)=(−2,−2)\)\((h+c,k)=(8,−2)\) e. Podemos usar a\(x\) coordenada -de qualquer um desses pontos para resolver\(c\). Usando o ponto\((8,−2)\) e substituindo\(h=3\),

\[\begin{align*} h+c&=8\\ 3+c&=8\\ c&=5\\ c^2&=25 \end{align*}\]

Em seguida, resolva\(b^2\) o uso da equação\(b^2=c^2−a^2\):

\[\begin{align*} b^2&=c^2-a^2\\ &=25-9\\ &=16 \end{align*}\]

Finalmente, substitua os valores encontrados por\(h\)\(k\)\(a^2\),, e\(b^2\) na forma padrão da equação.

\(\dfrac{{(x−3)}^2}{9}−\dfrac{{(y+2)}^2}{16}=1\)

Exercício\(\PageIndex{3}\)

Qual é a equação da forma padrão da hipérbole que tem vértices\((1,−2)\)\((1,8)\) e focos\((1,−10)\) e\((1,16)\)?

Responda

\(\dfrac{{(y−3)}^2}{25}+\dfrac{{(x−1)}^2}{144}=1\)

Representação gráfica de hipérboles centradas na origem

Quando temos uma equação na forma padrão para uma hipérbole centrada na origem, podemos interpretar suas partes para identificar as principais características de seu gráfico: o centro, vértices, co-vértices, assíntotas, focos e comprimentos e posições dos eixos transversal e conjugado. Para representar graficamente hipérboles centradas na origem, usamos a forma padrão\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\) para hipérboles horizontais e a forma padrão\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\) para hipérboles verticais.

Como: Dada uma equação de forma padrão para uma hipérbole centrada em\((0,0)\), sketch the graph

1. Determine qual das formas padrão se aplica à equação dada.
2. Use a forma padrão identificada na Etapa 1 para determinar a posição do eixo transversal; coordenadas para os vértices, co-vértices e focos; e as equações para as assíntotas.
   • Se a equação estiver no formulário\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), então
     • o eixo transversal está no\(x\) eixo -
     • as coordenadas dos vértices são\ ((\ pm a,0)\ 0
     • as coordenadas dos co-vértices são\((0,\pm b)\)
     • as coordenadas dos focos são\((\pm c,0)\)
     • as equações das assíntotas são\(y=\pm \dfrac{b}{a}x\)
   • Se a equação estiver no formulário\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\), então
     • o eixo transversal está no\(y\) eixo -
     • as coordenadas dos vértices são\((0,\pm a)\)
     • as coordenadas dos co-vértices são\((\pm b,0)\)
     • as coordenadas dos focos são\((0,\pm c)\)
     • as equações das assíntotas são\(y=\pm \dfrac{a}{b}x\)
3. Resolva as coordenadas dos focos usando a equação\(c=\pm \sqrt{a^2+b^2}\).
4. Faça um gráfico dos vértices, co-vértices, focos e assíntotas no plano coordenado e desenhe uma curva suave para formar a hipérbole.

Exemplo\(\PageIndex{4}\): Graphing a Hyperbola Centered at \((0,0)\) Given an Equation in Standard Form

Faça um gráfico da hipérbole dada pela equação\(\dfrac{y^2}{64}−\dfrac{x^2}{36}=1\). Identifique e rotule os vértices, co-vértices, focos e assíntotas.

Solução

A forma padrão que se aplica à equação dada é\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\). Assim, o eixo transversal está no\(y\) eixo -

As coordenadas dos vértices são\((0,\pm a)=(0,\pm \sqrt{64})=(0,\pm 8)\)

As coordenadas dos co-vértices são\((\pm b,0)=(\pm \sqrt{36}, 0)=(\pm 6,0)\)

As coordenadas dos focos são\((0,\pm c)\), onde\(c=\pm \sqrt{a^2+b^2}\). Resolvendo para\(c\), temos

\(c=\pm \sqrt{a^2+b^2}=\pm \sqrt{64+36}=\pm \sqrt{100}=\pm 10\)

Portanto, as coordenadas dos focos são\((0,\pm 10)\)

As equações das assíntotas são\(y=\pm \dfrac{a}{b}x=\pm \dfrac{8}{6}x=\pm \dfrac{4}{3}x\)

Plote e rotule os vértices e co-vértices e, em seguida, desenhe o retângulo central. Os lados do retângulo são paralelos aos eixos e passam pelos vértices e co-vértices. Desenhe e estenda as diagonais do retângulo central para mostrar as assíntotas. O retângulo central e as assíntotas fornecem a estrutura necessária para esboçar um gráfico preciso da hipérbole. Identifique os focos e assíntotas e desenhe uma curva suave para formar a hipérbole, conforme mostrado na Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\)

Exercício\(\PageIndex{4}\)

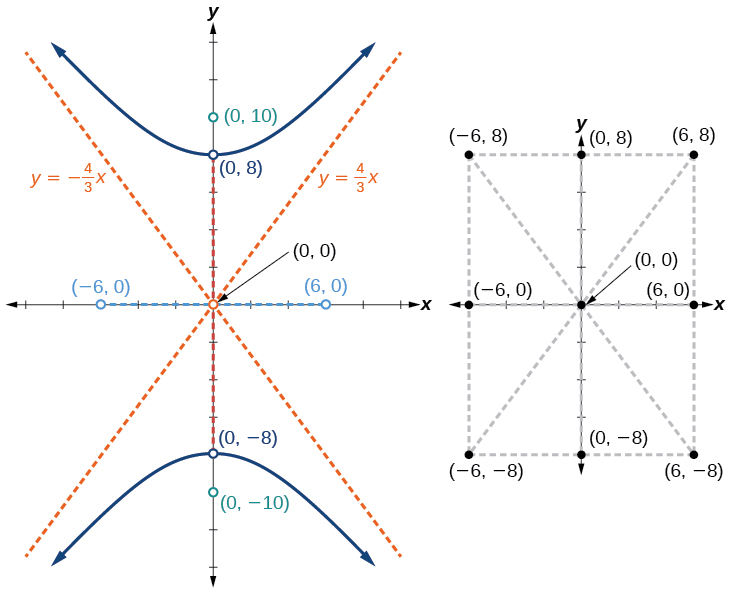
Faça um gráfico da hipérbole dada pela equação\(\dfrac{x^2}{144}−\dfrac{y^2}{81}=1\). Identifique e rotule os vértices, co-vértices, focos e assíntotas.

Responda

vértices:\((\pm 12,0)\); co-vértices:\((0,\pm 9)\); focos:\((\pm 15,0)\); assíntotas:\(y=\pm \dfrac{3}{4}x\);

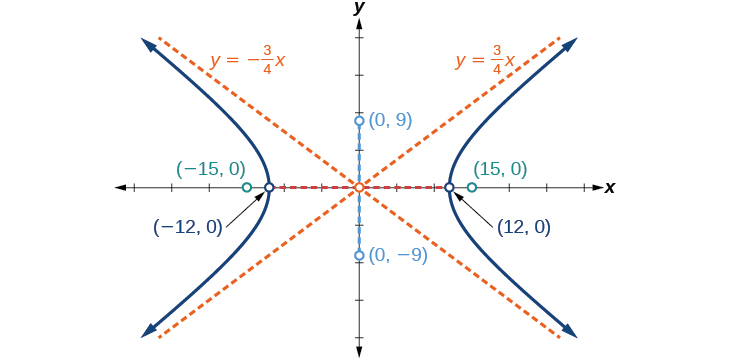
Figura\(\PageIndex{9}\)

Representação gráfica de hipérboles não centradas na origem

Representar graficamente hipérboles centradas em um ponto\((h,k)\) diferente da origem é semelhante à representação gráfica de elipses centradas em um ponto diferente da origem. Usamos as formas padrão\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\) para hipérboles horizontais e\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\) para hipérboles verticais. A partir dessas equações de forma padrão, podemos facilmente calcular e traçar as principais características do gráfico: as coordenadas de seu centro, vértices, co-vértices e focos; as equações de suas assíntotas; e as posições dos eixos transversal e conjugado.

Como: Dada uma forma geral para uma hipérbole centrada em\((h, k)\), sketch the graph

1. Converta o formulário geral nesse formulário padrão. Determine qual das formas padrão se aplica à equação dada.
2. Use a forma padrão identificada na Etapa 1 para determinar a posição do eixo transversal; coordenadas para o centro, vértices, co-vértices, focos; e equações para as assíntotas.
   1. Se a equação estiver no formulário\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), então
      • o eixo transversal é paralelo ao\(x\) eixo -
      • o centro é\((h,k)\)
      • as coordenadas dos vértices são\((h\pm a,k)\)
      • as coordenadas dos co-vértices são\((h,k\pm b)\)
      • as coordenadas dos focos são\((h\pm c,k)\)
      • as equações das assíntotas são\(y=\pm \dfrac{b}{a}(x−h)+k\)
   2. Se a equação estiver no formulário\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\), então
      • o eixo transversal é paralelo ao\(y\) eixo -
      • o centro é\((h,k)\)
      • as coordenadas dos vértices são\((h,k\pm a)\)
      • as coordenadas dos co-vértices são\((h\pm b,k)\)
      • as coordenadas dos focos são\((h,k\pm c)\)
      • as equações das assíntotas são\(y=\pm \dfrac{a}{b}(x−h)+k\)
3. Resolva as coordenadas dos focos usando a equação\(c=\pm \sqrt{a^2+b^2}\).
4. Faça um gráfico do centro, vértices, co-vértices, focos e assíntotas no plano coordenado e desenhe uma curva suave para formar a hipérbole.

Exemplo\(\PageIndex{5}\): Graphing a Hyperbola Centered at \((h, k)\) Given an Equation in General Form

Faça um gráfico da hipérbole dada pela equação\(9x^2−4y^2−36x−40y−388=0\). Identifique e rotule o centro, os vértices, os co-vértices, os focos e as assíntotas.

Solução

Comece expressando a equação na forma padrão. Agrupe termos que contêm a mesma variável e mova a constante para o lado oposto da equação.

\((9x^2−36x)−(4y^2+40y)=388\)

Fator o coeficiente principal de cada expressão.

\(9(x^2−4x)−4(y^2+10y)=388\)

Complete o quadrado duas vezes. Lembre-se de equilibrar a equação adicionando as mesmas constantes em cada lado.

\(9(x^2−4x+4)−4(y^2+10y+25)=388+36−100\)

Reescreva como quadrados perfeitos.

\(9{(x−2)}^2−4{(y+5)}^2=324\)

Divida os dois lados pelo termo constante para colocar a equação na forma padrão.

\(\dfrac{{(x−2)}^2}{36}−\dfrac{{(y+5)}^2}{81}=1\)

A forma padrão que se aplica à equação dada é\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\), onde\(a^2=36\)\(a=6\) e\(b^2=81\) ou\(b=9\) e. Assim, o eixo transversal é paralelo ao\(x\) eixo -. Daqui resulta que:

o centro da elipse é\((h,k)=(2,−5)\)

as coordenadas dos vértices são\((h\pm a,k)=(2\pm 6,−5)\), ou\((−4,−5)\) e\((8,−5)\)

as coordenadas dos co-vértices são\((h,k\pm b)=(2,−5\pm 9)\), ou\((2,−14)\) e\((2,4)\)

as coordenadas dos focos são\((h\pm c,k)\), onde\(c=\pm \sqrt{a^2+b^2}\). Resolvendo para\(c\), temos

\(c=\pm \sqrt{36+81}=\pm \sqrt{117}=\pm 3\sqrt{13}\)

Portanto, as coordenadas dos focos são\((2−3\sqrt{13},−5)\)\((2+3\sqrt{13},−5)\) e.

As equações das assíntotas são\(y=\pm \dfrac{b}{a}(x−h)+k=\pm \dfrac{3}{2}(x−2)−5\).

Em seguida, traçamos e rotulamos o centro, vértices, co-vértices, focos e assíntotas e desenhamos curvas suaves para formar a hipérbole, conforme mostrado na Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\)

Exercício\(\PageIndex{5}\)

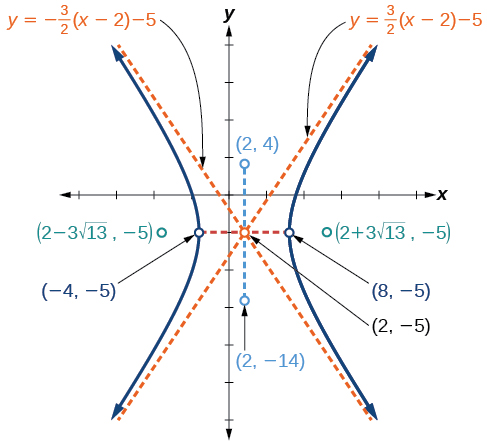
Faça um gráfico da hipérbole dada pela forma padrão de uma equação\(\dfrac{{(y+4)}^2}{100}−\dfrac{{(x−3)}^2}{64}=1\). Identifique e rotule o centro, os vértices, os co-vértices, os focos e as assíntotas.

Responda

centro:\((3,−4)\); vértices:\((3,−14)\) e\((3,6)\); co-vértices:\((−5,−4)\); e\((11,−4)\); focos:\((3,−4−2\sqrt{41})\) e\((3,−4+2\sqrt{41})\); assíntotas:\(y=\pm \dfrac{5}{4}(x−3)−4\)

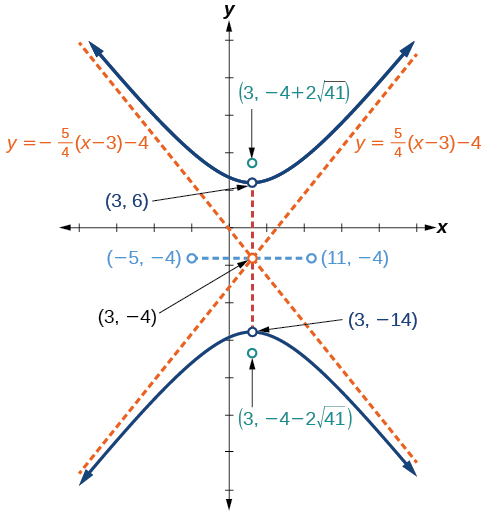
Figura\(\PageIndex{11}\)

Resolvendo problemas aplicados envolvendo hipérboles

Como discutimos no início desta seção, as hipérboles têm aplicações reais em muitos campos, como astronomia, física, engenharia e arquitetura. A eficiência do design das torres de resfriamento hiperbólicas é particularmente interessante. As torres de resfriamento são usadas para transferir calor residual para a atmosfera e são frequentemente elogiadas por sua capacidade de gerar energia com eficiência. Devido à sua forma hiperbólica, essas estruturas são capazes de resistir a ventos extremos, exigindo menos material do que qualquer outra forma de seu tamanho e resistência (Figura\(\PageIndex{12}\)). Por exemplo, uma torre\(500\) de pés pode ser feita de uma concha de concreto armado com apenas\(6\)\(8\) centímetros de largura!

Figura\(\PageIndex{12}\): Torres de resfriamento na usina de Drax em North Yorkshire, Reino Unido (crédito: Les Haines, Flickr)

As primeiras torres hiperbólicas foram projetadas em 1914 e tinham\(35\) metros de altura. Hoje, as torres de resfriamento mais altas estão na França, com uma altura notável de\(170\) metros. No exemplo,\(\PageIndex{6}\) usaremos o layout de design de uma torre de resfriamento para encontrar uma equação hiperbólica que modela seus lados.

Exemplo\(\PageIndex{6}\): Solving Applied Problems Involving Hyperbolas

O layout do design de uma torre de resfriamento é mostrado na Figura\(\PageIndex{13}\). A torre tem\(179.6\) metros de altura. O diâmetro da parte superior é de\(72\) metros. No seu ponto mais próximo, os lados da torre estão separados por\(60\) metros.

Figura\(\PageIndex{13}\): Projeto de uma torre de resfriamento de tiragem natural

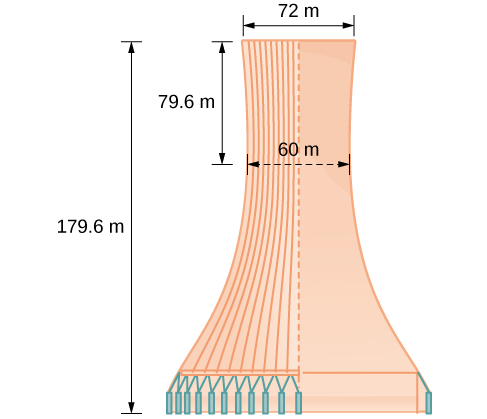
Encontre a equação da hipérbole que modela os lados da torre de resfriamento. Suponha que o centro da hipérbole — indicado pela interseção das linhas perpendiculares tracejadas na figura — seja a origem do plano coordenado. Arredonde os valores finais para quatro casas decimais.

Solução

Estamos assumindo que o centro da torre está na origem, então podemos usar a forma padrão de uma hipérbole horizontal centrada na origem:\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\), onde os galhos da hipérbole formam as laterais da torre de resfriamento. Precisamos encontrar os valores de\(a^2\) e\(b^2\) para completar o modelo.

Primeiro, encontramos\(a^2\). Lembre-se de que o comprimento do eixo transversal de uma hipérbole é\(2a\). Esse comprimento é representado pela distância em que os lados estão mais próximos, que é dada em\(65.3\) metros. Então,\(2a=60\). Portanto,\(a=30\)\(a^2=900\) e.

Para resolver\(b^2\), precisamos substituir\(x\) e\(y\) em nossa equação usando um ponto conhecido. Para fazer isso, podemos usar as dimensões da torre para encontrar algum ponto\((x,y)\) que esteja na hipérbole. Usaremos o canto superior direito da torre para representar esse ponto. Como o\(y\) eixo -divide a torre ao meio, nosso\(x\) valor -pode ser representado pelo raio do topo, ou\(36\) metros. O valor y é representado pela distância da origem até o topo, que é dada como\(79.6\) metros. Portanto,

\[\begin{align*} \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}&=1\qquad \text{Standard form of horizontal hyperbola.}\\ b^2&=\dfrac{y^2}{\dfrac{x^2}{a^2}-1}\qquad \text{Isolate } b^2\\ &=\dfrac{{(79.6)}^2}{\dfrac{{(36)}^2}{900}-1}\qquad \text{Substitute for } a^2,\: x, \text{ and } y\\ &\approx 14400.3636\qquad \text{Round to four decimal places} \end{align*}\]

Os lados da torre podem ser modelados pela equação hiperbólica

\(\dfrac{x^2}{900}−\dfrac{y^2}{14400.3636}=1\), ou\(\dfrac{x^2}{{30}^2}−\dfrac{y^2}{{120.0015}^2}=1\)

Exercício\(\PageIndex{6}\)

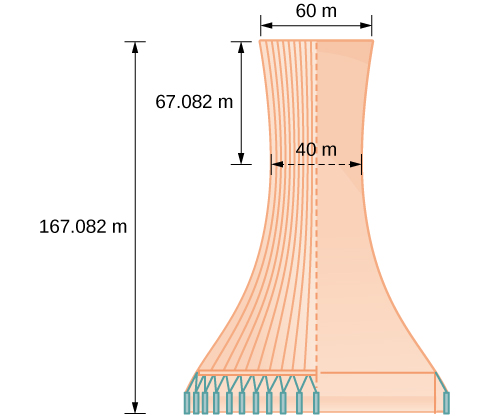
Um design para um projeto de torre de resfriamento é mostrado na Figura\(\PageIndex{14}\). Encontre a equação da hipérbole que modela os lados da torre de resfriamento. Suponha que o centro da hipérbole — indicado pela interseção das linhas perpendiculares tracejadas na figura — seja a origem do plano coordenado. Arredonde os valores finais para quatro casas decimais.

Figura\(\PageIndex{14}\)

Responda

Os lados da torre podem ser modelados pela equação hiperbólica. \(\dfrac{x^2}{400}−\dfrac{y^2}{3600}=1\)ou\(\dfrac{x^2}{{20}^2}−\dfrac{y^2}{{60}^2}=1\).

Mídia

Acesse esses recursos on-line para obter instruções adicionais e praticar com hipérboles.

• Seções cônicas: A hipérbole, parte 1 de 2
• Seções cônicas: A hipérbole, parte 2 de 2
• Representar graficamente uma hipérbole com o centro
• Faça um gráfico de uma hipérbole com o centro não na origem

Equações-chave

Hipérbole, centro na origem, eixo transversal no eixo x	\(\dfrac{x^2}{a^2}−\dfrac{y^2}{b^2}=1\)
Hipérbole, centro na origem, eixo transversal no eixo y	\(\dfrac{y^2}{a^2}−\dfrac{x^2}{b^2}=1\)
Hipérbole\((h,k)\), centro em, eixo transversal paralelo ao eixo x	\(\dfrac{{(x−h)}^2}{a^2}−\dfrac{{(y−k)}^2}{b^2}=1\)
Hipérbole\((h,k)\), centro em, eixo transversal paralelo ao eixo y	\(\dfrac{{(y−k)}^2}{a^2}−\dfrac{{(x−h)}^2}{b^2}=1\)

Conceitos-chave

• Uma hipérbole é o conjunto de todos os pontos\((x,y)\) em um plano, de forma que a diferença das distâncias entre\((x,y)\) e os focos seja uma constante positiva.
• A forma padrão de uma hipérbole pode ser usada para localizar seus vértices e focos. Veja o exemplo\(\PageIndex{1}\).
• Quando dadas as coordenadas dos focos e vértices de uma hipérbole, podemos escrever a equação da hipérbole na forma padrão. Veja o exemplo\(\PageIndex{2}\) e o exemplo\(\PageIndex{3}\).
• Quando recebemos uma equação para uma hipérbole, podemos identificar seus vértices, co-vértices, focos, assíntotas e comprimentos e posições dos eixos transversal e conjugado para representar graficamente a hipérbole. Veja o exemplo\(\PageIndex{4}\) e o exemplo\(\PageIndex{5}\).
• Situações do mundo real podem ser modeladas usando as equações padrão das hipérboles. Por exemplo, dadas as dimensões de uma torre de resfriamento de tiragem natural, podemos encontrar uma equação hiperbólica que modela seus lados. Veja o exemplo\(\PageIndex{6}\).