9.5: Resolvendo equações trigonométricas
- Page ID
- 186883
- Resolva equações trigonométricas lineares em seno e cosseno.
- Resolva equações envolvendo uma única função trigonométrica.
- Resolva equações trigonométricas usando uma calculadora.
- Resolva equações trigonométricas com formato quadrático.
- Resolva equações trigonométricas usando identidades fundamentais.
- Resolva equações trigonométricas com vários ângulos.
- Resolva problemas do triângulo reto.
Tales de Mileto (cerca de 625—547 a.C.) é conhecido como o fundador da geometria. A lenda diz que ele calculou a altura da Grande Pirâmide de Gizé, no Egito, usando a teoria de triângulos semelhantes, que ele desenvolveu medindo a sombra de seu cajado. Com base em proporções, essa teoria tem aplicações em várias áreas, incluindo geometria fractal, engenharia e arquitetura. Freqüentemente, o ângulo de elevação e o ângulo de depressão são encontrados usando triângulos semelhantes.

Nas seções anteriores deste capítulo, analisamos as identidades trigonométricas. As identidades são verdadeiras para todos os valores no domínio da variável. Nesta seção, começamos nosso estudo de equações trigonométricas para estudar cenários do mundo real, como a descoberta das dimensões das pirâmides.
Resolvendo equações trigonométricas lineares em seno e cosseno
Equações trigonométricas são, como o nome indica, equações que envolvem funções trigonométricas. Semelhante em muitos aspectos à resolução de equações polinomiais ou equações racionais, somente valores específicos da variável serão soluções, se houver alguma solução. Freqüentemente, resolveremos uma equação trigonométrica em um intervalo especificado. No entanto, com a mesma frequência, seremos solicitados a encontrar todas as soluções possíveis e, como as funções trigonométricas são periódicas, as soluções são repetidas em cada período. Em outras palavras, as equações trigonométricas podem ter um número infinito de soluções. Além disso, como as equações racionais, o domínio da função deve ser considerado antes de assumirmos que qualquer solução é válida. O período da função seno e da função cosseno é\(2\pi\). Em outras palavras, a cada\(2\pi\) unidade, os valores de y se repetem. Se precisarmos encontrar todas as soluções possíveis, devemos adicionar\(2\pi k\), onde\(k\) está um número inteiro, à solução inicial. Lembre-se da regra que fornece o formato para declarar todas as soluções possíveis para uma função em que o período é\(2\pi\):
\[\sin \theta=\sin(\theta \pm 2k\pi)\]
Existem regras semelhantes para indicar todas as soluções possíveis para as outras funções trigonométricas. Resolver equações trigonométricas requer as mesmas técnicas que resolver equações algébricas. Lemos a equação da esquerda para a direita, horizontalmente, como uma frase. Procuramos padrões conhecidos, fatoramos, encontramos denominadores comuns e substituímos certas expressões por uma variável para tornar a solução um processo mais simples. No entanto, com equações trigonométricas, também temos a vantagem de usar as identidades que desenvolvemos nas seções anteriores.
Encontre todas as soluções exatas possíveis para a equação\(\cos \theta=\dfrac{1}{2}\).
Solução
Do círculo unitário, sabemos que
\[ \begin{align*} \cos \theta &=\dfrac{1}{2} \\[4pt] \theta &=\dfrac{\pi}{3},\space \dfrac{5\pi}{3} \end{align*}\]
Essas são as soluções no intervalo\([ 0,2\pi ]\). Todas as soluções possíveis são fornecidas por
\[\theta=\dfrac{\pi}{3} \pm 2k\pi \quad \text{and} \quad \theta=\dfrac{5\pi}{3} \pm 2k\pi \nonumber\]
onde\(k\) é um número inteiro.
Encontre todas as soluções exatas possíveis para a equação\(\sin t=\dfrac{1}{2}\).
Solução
Resolver todos os valores possíveis\(t\) significa que as soluções incluem ângulos além do período de\(2\pi\). Na seção sobre identidades de soma e diferença, podemos ver que as soluções são\(t=\dfrac{\pi}{6}\)\(t=\dfrac{5\pi}{6}\) e. Mas o problema é pedir todos os valores possíveis que resolvam a equação. Portanto, a resposta é
\[t=\dfrac{\pi}{6}\pm 2\pi k \quad \text{and} \quad t=\dfrac{5\pi}{6}\pm 2\pi k \nonumber\]
onde\(k\) é um número inteiro.
- Procure um padrão que sugira uma propriedade algébrica, como a diferença de quadrados ou uma oportunidade de fatoração.
- Substitua a expressão trigonométrica por uma única variável, como\(x\) ou\(u\).
- Resolva a equação da mesma forma que uma equação algébrica seria resolvida.
- Substitua novamente a expressão trigonométrica pela variável nas expressões resultantes.
- Resolva o ângulo.
Resolva a equação exatamente:\(2 \cos \theta−3=−5\),\(0≤\theta<2\pi\).
Solução
Use técnicas algébricas para resolver a equação.
\[\begin{align*} 2 \cos \theta-3&= -5\\ 2 \cos \theta&= -2\\ \cos \theta&= -1\\ \theta&= \pi \end{align*}\]
Resolva exatamente a seguinte equação linear no intervalo\([0,2\pi)\):\(2 \sin x+1=0\).
- Resposta
-
\(x=\dfrac{7\pi}{6},\space \dfrac{11\pi}{6}\)
Resolvendo equações envolvendo uma única função trigonométrica
Quando recebemos equações que envolvem apenas uma das seis funções trigonométricas, suas soluções envolvem o uso de técnicas algébricas e o círculo unitário (veja [link]). Precisamos fazer várias considerações quando a equação envolve funções trigonométricas diferentes do seno e do cosseno. Os problemas envolvendo os recíprocos das funções trigonométricas primárias precisam ser vistos de uma perspectiva algébrica. Em outras palavras, escreveremos a função recíproca e resolveremos os ângulos usando a função. Além disso, uma equação envolvendo a função tangente é ligeiramente diferente daquela que contém uma função seno ou cosseno. Primeiro, como sabemos, o período da tangente é\(\pi\), não\(2\pi\). Além disso, o domínio da tangente são todos números reais, com exceção dos múltiplos inteiros ímpares de\(\dfrac{\pi}{2}\), a menos, é claro, que um problema imponha suas próprias restrições ao domínio.
Resolva o problema exatamente:\(2 {\sin}^2 \theta−1=0\),\(0≤\theta<2\pi\).
Solução
Como esse problema não é facilmente fatorado, resolveremos usando a propriedade de raiz quadrada. Primeiro, usamos álgebra para isolar\(\sin \theta\). Em seguida, encontraremos os ângulos.
\ [\ begin {align*}
2 {\ sin} ^2\ theta-1&= 0\\
2 {\ sin} ^2\ theta&= 1\\
{\ sin} ^2\ theta&=\ dfrac {1} {2}\
\ sqrt {{\ sin} ^2\ theta} &=\ pm\ sqrt {\ dfrac {1} {2}\\
\ sin\ theta&=\ pm\ dfrac {1} {\ sqrt {2}}\\
&=\ pm\ dfrac {\ sqrt {2}} {2}\\
\ theta&=\ dfrac {\ pi} {4},\ space\ dfrac {3\ pi} {4},\ space\ dfrac {5\ pi} {4},\ space\ dfrac {7\ pi} {4}
\ end {align*}\]
Resolva exatamente a seguinte equação:\(\csc \theta=−2\),\(0≤\theta<4\pi\).
Solução
Queremos todos os valores dos\(\theta\) quais\(\csc \theta=−2\) ao longo do intervalo\(0≤\theta<4\pi\).
\[\begin{align*} \csc \theta&= -2\\ \dfrac{1}{\sin \theta}&= -2\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\space \dfrac{11\pi}{6},\space \dfrac{19\pi}{6}, \space \dfrac{23\pi}{6} \end{align*}\]
Análise
Como\(\sin \theta=−\dfrac{1}{2}\), observe que todas as quatro soluções estão no terceiro e quarto quadrantes.
Resolva a equação exatamente:\(\tan\left(\theta−\dfrac{\pi}{2}\right)=1\),\(0≤\theta<2\pi\).
Solução
Lembre-se de que a função tangente tem um período de\(\pi\). No intervalo\([ 0,\pi )\) e no ângulo de\(\dfrac{\pi}{4}\), a tangente tem um valor de\(1\). No entanto, o ângulo que queremos é\(\left(\theta−\dfrac{\pi}{2}\right)\). Assim, se\(\tan\left(\dfrac{\pi}{4}\right)=1\), então
\[\begin{align*} \theta-\dfrac{\pi}{2}&= \dfrac{\pi}{4}\\ \theta&= \dfrac{3\pi}{4} \pm k\pi \end{align*}\]
Ao longo do intervalo\([ 0,2\pi )\), temos duas soluções:
\(\theta=\dfrac{3\pi}{4}\)e\(\theta=\dfrac{3\pi}{4}+\pi=\dfrac{7\pi}{4}\)
Encontre todas as soluções para\(\tan x=\sqrt{3}\).
- Resposta
-
\(\dfrac{\pi}{3}\pm \pi k\)
Identifique todas as soluções exatas para a equação\(2(\tan x+3)=5+\tan x\),\(0≤x<2\pi\).
Solução
Podemos resolver essa equação usando apenas álgebra. Isole a expressão\(\tan x\) no lado esquerdo do sinal de igual.
\[\begin{align*} 2(\tan x)+2(3)&= 5+\tan x\\ 2\tan x+6&= 5+\tan x\\ 2\tan x-\tan x&= 5-6\\ \tan x&= -1 \end{align*}\]
Existem dois ângulos no círculo unitário que têm um valor tangente de\(−1\):\(\theta=\dfrac{3\pi}{4}\)\(\theta=\dfrac{7\pi}{4}\) e.
Resolva equações trigonométricas usando uma calculadora
Nem todas as funções podem ser resolvidas exatamente usando apenas o círculo unitário. Quando precisamos resolver uma equação envolvendo um ângulo diferente de um dos ângulos especiais, precisaremos usar uma calculadora. Verifique se ele está configurado no modo correto, em graus ou radianos, dependendo dos critérios do problema em questão.
Use uma calculadora para resolver a equação\(\sin \theta=0.8\), onde\(\theta\) está em radianos.
Solução
Verifique se o modo está configurado para radianos. Para encontrar\(\theta\), use a função seno inverso. Na maioria das calculadoras, você precisará pressionar o botão 2 ND e, em seguida, o botão SIN para abrir a\({\sin}^{−1}\) função. O que é mostrado na tela é\({\sin}^{−1}\) .A calculadora está pronta para a entrada entre parênteses. Para esse problema\({\sin}^{−1}(0.8)\), entramos e pressionamos ENTER. Assim, até quatro casas decimais,
\({\sin}^{−1}(0.8)≈0.9273\)
A solução é
\(\theta≈0.9273\pm 2\pi k\)
A medição do ângulo em graus é
\[\begin{align*} \theta&\approx 53.1^{\circ}\\ \theta&\approx 180^{\circ}-53.1^{\circ}\\ &\approx 126.9^{\circ} \end{align*}\]
Análise
Observe que uma calculadora retornará apenas um ângulo nos quadrantes I ou IV para a função seno, já que esse é o intervalo do seno inverso. O outro ângulo é obtido usando\(\pi−\theta\).
Use uma calculadora para resolver a equação que\( \sec θ=−4, \) dá sua resposta em radianos.
Solução
Podemos começar com um pouco de álgebra.
\[\begin{align*} \sec \theta&= -4\\ \dfrac{1}{\cos \theta}&= -4\\ \cos \theta&= -\dfrac{1}{4} \end{align*}\]
Verifique se o MODO está em radianos. Agora use a função inversa do cosseno
\[\begin{align*}{\cos}^{-1}\left(-\dfrac{1}{4}\right)&\approx 1.8235\\ \theta&\approx 1.8235+2\pi k \end{align*}\]
Como\(\dfrac{\pi}{2}≈1.57\) e\(\pi≈3.14\),\(1.8235\) está entre esses dois números,\(\theta≈1.8235\) está no quadrante II. O cosseno também é negativo no quadrante III. Observe que uma calculadora retornará apenas um ângulo nos quadrantes I ou II para a função cosseno, já que esse é o intervalo do cosseno inverso. Veja a Figura\(\PageIndex{2}\).
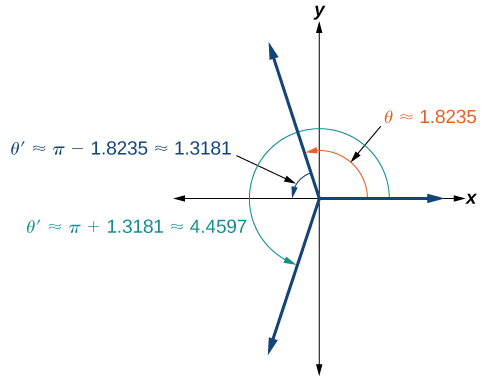
Então, também precisamos encontrar a medida do ângulo no quadrante III. No quadrante III, o ângulo de referência é\(\theta '≈\pi−1.8235≈1.3181\). A outra solução no quadrante III é\(\theta '≈\pi+1.3181≈4.4597\).
As soluções são\(\theta≈1.8235\pm 2\pi k\)\(\theta≈4.4597\pm 2\pi k\) e.
Resolver\(\cos \theta=−0.2\).
- Resposta
-
\(\theta≈1.7722\pm 2\pi k\)e\(\theta≈4.5110\pm 2\pi k\)
Resolvendo equações trigonométricas em forma quadrática
Resolver uma equação quadrática pode ser mais complicado, mas, mais uma vez, podemos usar a álgebra como faríamos com qualquer equação quadrática. Veja o padrão da equação. Há mais de uma função trigonométrica na equação ou há apenas uma? Qual função trigonométrica é quadrada? Se houver apenas uma função representada e um dos termos for quadrado, pense na forma padrão de uma quadrática. Substitua a função trigonométrica por uma variável como\(x\) ou\(u\). Se a substituição fizer com que a equação pareça uma equação quadrática, então podemos usar os mesmos métodos para resolver as equações quadráticas para resolver as equações trigonométricas.
Resolva a equação exatamente:\({\cos}^2 \theta+3 \cos \theta−1=0\),\(0≤\theta<2\pi\).
Solução
Começamos usando a substituição e\(\cos \theta\) substituindo por\(x\). Não é necessário usar a substituição, mas isso pode facilitar a resolução visual do problema. Deixe\(\cos \theta=x\). Nós temos
\(x^2+3x−1=0\)
A equação não pode ser fatorada, então usaremos a fórmula quadrática:\(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\).
\[\begin{align*} x&= \dfrac{ -3\pm \sqrt{ {(-3)}^2-4 (1) (-1) } }{2}\\ &= \dfrac{-3\pm \sqrt{13}}{2}\end{align*}\]
\(x\)Substitua por\(\cos \theta \) e resolva.
\[\begin{align*} \cos \theta&= \dfrac{-3\pm \sqrt{13}}{2}\\ \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right) \end{align*}\]
Observe que somente o sinal + é usado. Isso ocorre porque obtemos um erro quando resolvemos\(\theta={\cos}^{−1}\left(\dfrac{−3−\sqrt{13}}{2}\right)\) em uma calculadora, já que o domínio da função inversa do cosseno é\([ −1,1 ]\). No entanto, há uma segunda solução:
\[\begin{align*} \theta&= {\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 1.26 \end{align*}\]
Este lado terminal do ângulo está no quadrante I. Como o cosseno também é positivo no quadrante IV, a segunda solução é
\[\begin{align*} \theta&= 2\pi-{\cos}^{-1}\left(\dfrac{-3+\sqrt{13}}{2}\right)\\ &\approx 5.02 \end{align*}\]
Resolva a equação exatamente:\(2 {\sin}^2 \theta−5 \sin \theta+3=0\),\(0≤\theta≤2\pi\).
Solução
Usando o agrupamento, essa quadrática pode ser fatorada. Ou faça a substituição real\(\sin \theta=u\), ou imagine-a, à medida que consideramos:
\[\begin{align*} 2 {\sin}^2 \theta-5 \sin \theta+3&= 0\\ (2 \sin \theta-3)(\sin \theta-1)&= 0 \qquad \text {Now set each factor equal to zero.}\\ 2 \sin \theta-3&= 0\\ 2 \sin \theta&= 3\\ \sin \theta&= \dfrac{3}{2}\\ \sin \theta-1&= 0\\ \sin \theta&= 1 \end{align*}\]
Em seguida, resolva para\(\theta\):\(\sin \theta≠\dfrac{3}{2}\), como é o intervalo da função seno\([ −1,1 ]\). No entanto\(\sin \theta=1\), dando a solução\(\theta=\dfrac{\pi}{2}\).
Análise
Certifique-se de verificar todas as soluções em um determinado domínio, pois alguns fatores não têm solução.
Resolver\({\sin}^2 \theta=2 \cos \theta+2\),\(0≤\theta≤2\pi\). [Dica: Faça uma substituição para expressar a equação somente em termos de cosseno.]
- Resposta
-
\(\cos \theta=−1\),\(\theta=\pi\)
Resolva exatamente:\(2 {\sin}^2 \theta+\sin \theta=0;\space 0≤\theta<2\pi\)
Solução
Esse problema deve parecer familiar, pois é semelhante a um quadrático. Deixe\(\sin \theta=x\). A equação se torna\(2x^2+x=0\). Começamos considerando:
\ [\ begin {align*}
2x^2+x&= 0\\
x (2x+1) &= 0\ qquad\ text {Defina cada fator igual a zero.} \\
x&= 0\\
2x+1&= 0\\
x&= -\ dfrac {1} {2}\ end {align*}\]
Em seguida, substitua novamente na equação a expressão\(\sin \theta \) original\(x\). Assim,
\ [\ begin {align*}\ sin\ theta&= 0\\
\ theta&= 0,\ pi\\
\ sin\ theta&= -\ dfrac {1} {2}\\
\ theta&=\ dfrac {7\ pi} {6},\ dfrac {11\ pi} {6}
\ end {align*}\]
As soluções dentro do domínio\(0≤\theta<2\pi\) são\(\theta=0,\pi,\dfrac{7\pi}{6},\dfrac{11\pi}{6}\).
Se preferirmos não substituir, podemos resolver a equação seguindo o mesmo padrão de fatoração e definindo cada fator igual a zero.
\[\begin{align*} {\sin}^2 \theta+\sin \theta&= 0\\ \sin \theta(2\sin \theta+1)&= 0\\ \sin \theta&= 0\\ \theta&= 0,\pi\\ 2 \sin \theta+1&= 0\\ 2\sin \theta&= -1\\ \sin \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{7\pi}{6},\dfrac{11\pi}{6} \end{align*}\]
Análise
Podemos ver as soluções no gráfico na Figura\(\PageIndex{3}\). No intervalo\(0≤\theta<2\pi\), o gráfico cruza o eixo\(x\) - quatro vezes, nas soluções anotadas. Observe que as equações trigonométricas que estão na forma quadrática podem produzir até quatro soluções em vez das duas esperadas que são encontradas com equações quadráticas. Neste exemplo, cada solução (ângulo) correspondente a um valor senoidal positivo produzirá dois ângulos que resultariam nesse valor.
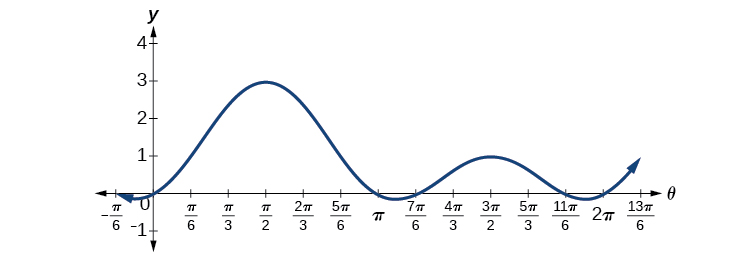
Também podemos verificar as soluções no círculo unitário por meio do resultado na seção sobre Identidades de Soma e Diferença.
Resolva a equação quadrática na forma exata:\(2 {\sin}^2 \theta−3 \sin \theta+1=0\),\(0≤\theta<2\pi\).
Solução
Podemos fatorar usando o agrupamento. Os valores da solução de\(\theta\) podem ser encontrados no círculo unitário.
\[\begin{align*} (2 \sin \theta-1)(\sin \theta-1)&= 0\\ 2 \sin \theta-1&= 0\\ \sin \theta&= \dfrac{1}{2}\\ \theta&= \dfrac{\pi}{6}, \dfrac{5\pi}{6}\\ \sin \theta&= 1\\ \theta&= \dfrac{\pi}{2} \end{align*}\]
Resolva a equação quadrática\(2{\cos}^2 \theta+\cos \theta=0\).
- Resposta
-
\(\dfrac{\pi}{2}, \space \dfrac{2\pi}{3}, \space \dfrac{4\pi}{3}, \space \dfrac{3\pi}{2}\)
Resolvendo equações trigonométricas usando identidades fundamentais
Embora a álgebra possa ser usada para resolver várias equações trigonométricas, também podemos usar as identidades fundamentais porque elas simplificam a resolução de equações. Lembre-se de que as técnicas que usamos para resolver não são as mesmas para verificar identidades. As regras básicas da álgebra se aplicam aqui, em vez de reescrever um lado da identidade para coincidir com o outro lado. No próximo exemplo, usamos duas identidades para simplificar a equação.
Use identidades para resolver exatamente a equação trigonométrica ao longo do intervalo\(0≤x<2\pi\).
\(\cos x \cos(2x)+\sin x \sin(2x)=\dfrac{\sqrt{3}}{2}\)
Solução
Observe que o lado esquerdo da equação é a fórmula da diferença para o cosseno.
\[\begin{align*} \cos x \cos(2x)+\sin x \sin(2x)&= \dfrac{\sqrt{3}}{2}\\ \cos(x-2x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Difference formula for cosine}\\ \cos(-x)&= \dfrac{\sqrt{3}}{2}\qquad \text{Use the negative angle identity.}\\ \cos x&= \dfrac{\sqrt{3}}{2} \end{align*}\]
A partir do círculo unitário na seção sobre identidades de soma e diferença, vemos que\(\cos x=\dfrac{\sqrt{3}}{2}\) quando\(x=\dfrac{\pi}{6},\space \dfrac{11\pi}{6}\).
Resolva a equação exatamente usando uma fórmula de ângulo duplo:\(\cos(2\theta)=\cos \theta\).
Solução
Temos três opções de expressões para substituir o ângulo duplo do cosseno. Como é mais simples resolver uma função trigonométrica por vez, escolheremos a identidade de ângulo duplo envolvendo apenas o cosseno:
\[\begin{align*} \cos(2\theta)&= \cos \theta\\ 2{\cos}^2 \theta-1&= \cos \theta\\ 2 {\cos}^2 \theta-\cos \theta-1&= 0\\ (2 \cos \theta+1)(\cos \theta-1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \cos \theta-1&= 0\\ \cos \theta&= 1 \end{align*}\]
Então, se\(\cos \theta=−\dfrac{1}{2}\), então\(\theta=\dfrac{2\pi}{3}\pm 2\pi k\) e\(\theta=\dfrac{4\pi}{3}\pm 2\pi k\); se\(\cos \theta=1\), então\(\theta=0\pm 2\pi k\).
Resolva a equação exatamente usando uma identidade:\(3 \cos \theta+3=2 {\sin}^2 \theta\),\(0≤\theta<2\pi\).
Solução
Se reescrevermos o lado direito, podemos escrever a equação em termos de cosseno:
\ [\ begin {align*}
3\ cos\ theta+3&= 2 {\ sin} ^2\ theta\\
3\ cos\ theta+3&= 2 (1- {\ cos} ^2\ theta)\\
3\ cos\ theta+3&= 2-2 {\ cos} ^2\ theta\\
2 {\ cos} ^2\ theta+3\ cos a+1&= 0\\
(2\ cos\ theta+1) (\ cos\ theta+1) &= 0\\
2\ cos\ theta+1&= 0\\\ cos
\ theta&= -\ dfrac {1} {2}\\\ theta&=
\ dfrac {2\ pi} {3},\ space\ dfrac {4\ pi} {3}\\ cos\ theta+1&= 0\
\\ cos\ theta&= -1\\\
theta&= -1\\\ theta&= -1\
\\ theta&=\\ pi\
\\ end {align*}\]
Nossas soluções são\(\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi\).
Resolvendo equações trigonométricas com vários ângulos
Às vezes, não é possível resolver uma equação trigonométrica com identidades que tenham um ângulo múltiplo, como\(\sin(2x)\) ou\(\cos(3x)\). Quando confrontado com essas equações, lembre-se de que\(y=\sin(2x)\) é uma compressão horizontal por um fator de 2 da função\(y=\sin x\). Em um intervalo de\(2\pi\), podemos representar graficamente dois períodos de\(y=\sin(2x)\), em oposição a um ciclo de\(y=\sin x\). Essa compressão do gráfico nos leva a acreditar que pode haver duas vezes mais interceptações ou soluções x\(\sin(2x)=0\) em comparação com\(\sin x=0\). Essas informações nos ajudarão a resolver a equação.
Resolva exatamente:\(\cos(2x)=\dfrac{1}{2}\) não\([ 0,2\pi )\).
Solução
Podemos ver que essa equação é a equação padrão com um múltiplo de um ângulo. Se\(\cos(\alpha)=\dfrac{1}{2}\), sabemos que\(\alpha\) está nos quadrantes I e IV. Embora\(\theta={\cos}^{−1} \dfrac{1}{2}\) só produza soluções nos quadrantes I e II, reconhecemos que as soluções para a equação\(\cos \theta=\dfrac{1}{2}\) estarão nos quadrantes I e IV.
Portanto, os ângulos possíveis são\(\theta=\dfrac{\pi}{3}\)\(\theta=\dfrac{5\pi}{3}\) e. Então,\(2x=\dfrac{\pi}{3}\) ou\(2x=\dfrac{5\pi}{3}\), o que significa isso\(x=\dfrac{\pi}{6}\) ou\(x=\dfrac{5\pi}{6}\). Isso faz sentido? Sim, porque\(\cos\left(2\left(\dfrac{\pi}{6}\right)\right)=\cos\left(\dfrac{\pi}{3}\right)=\dfrac{1}{2}\).
Existem outras respostas possíveis? Vamos voltar ao nosso primeiro passo.
No quadrante I\(2x=\dfrac{\pi}{3}\),\(x=\dfrac{\pi}{6}\) conforme observado. Vamos girar em torno do círculo novamente:
\ [\ begin {align*}
2x&=\ dfrac {\ pi} {3} +2\ pi\\
&=\ dfrac {\ pi} {3} +\ dfrac {6\ pi} {3}\\
&=\ dfrac {7\ pi} {3}\\
x&=\ dfrac {7\ pi} {6}\\
\ text {Mais um a rotação produz}\\
2x&=\ dfrac {\ pi} {3} +4\ pi\\
& ; =\ dfrac {\ pi} {3} +\ dfrac {12\ pi} {3}\\
&=\ dfrac {13\ pi} {3}\
\ end {align*}\]
\(x=\dfrac{13\pi}{6}>2\pi\), então esse valor para\(x\) é maior que\(2\pi\), portanto, não é uma solução em\([ 0,2\pi )\).
No quadrante IV\(2x=\dfrac{5\pi}{3}\), assim\(x=\dfrac{5\pi}{6}\) como observado. Vamos girar em torno do círculo novamente:
\[\begin{align*} 2x&= \dfrac{5\pi}{3}+2\pi\\ &= \dfrac{5\pi}{3}+\dfrac{6\pi}{3}\\ &= \dfrac{11\pi}{3} \end{align*}\]
então\(x=\dfrac{11\pi}{6}\).
Mais uma rotação rende
\[\begin{align*} 2x&= \dfrac{5\pi}{3}+4\pi\\ &= \dfrac{5\pi}{3}+\dfrac{12\pi}{3}\\ &= \dfrac{17\pi}{3} \end{align*}\]
\(x=\dfrac{17\pi}{6}>2\pi\), então esse valor para\(x\) é maior que\(2\pi\), portanto, não é uma solução em\([ 0,2\pi )\).
Nossas soluções são\(x=\dfrac{\pi}{6}, \space \dfrac{5\pi}{6}, \space \dfrac{7\pi}{6}\),\(\dfrac{11\pi}{6}\) e. Observe que sempre que resolvemos um problema na forma de\(sin(nx)=c\), devemos contornar os\(n\) tempos unitários do círculo.
Resolvendo problemas do triângulo reto
Agora podemos usar todos os métodos que aprendemos para resolver problemas que envolvem a aplicação das propriedades dos triângulos retos e do Teorema de Pitágoras. Começamos com o conhecido Teorema de Pitágoras,
\[a^2+b^2=c^2 \label{Pythagorean}\]
e modele uma equação para se adequar a uma situação.
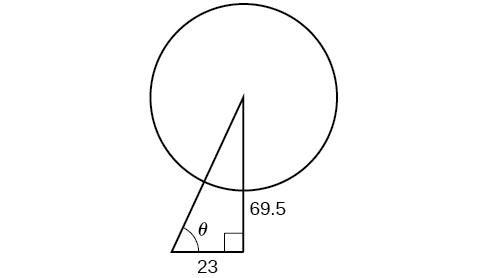
Um dos cabos que ancora o centro da roda gigante London Eye ao solo deve ser substituído. O centro da roda gigante está\(69.5\) metros acima do solo e a segunda âncora no solo está a\(23\) metros da base da roda gigante. Aproximadamente quanto tempo dura o cabo e qual é o ângulo de elevação (do solo até o centro da roda gigante)? Veja a Figura\(\PageIndex{4}\).
Solução
Use o Teorema de Pitágoras (Equação\ ref {Pitagórico}) e as propriedades dos triângulos retos para modelar uma equação que se encaixa no problema. Usando as informações fornecidas, podemos desenhar um triângulo reto. Podemos encontrar o comprimento do cabo com o Teorema de Pitágoras.
\[\begin{align*} a^2+b^2&= c^2\\ {(23)}^2+{(69.5)}^2&\approx 5359\\ \sqrt{5359}&\approx 73.2\space m \end{align*}\]
O ângulo de elevação é\(\theta\) formado pela segunda âncora no solo e pelo cabo que chega ao centro da roda. Podemos usar a função tangente para encontrar sua medida. Arredonde para duas casas decimais.
\[\begin{align*} \tan \theta&= 69.523\\ {\tan}^{-1}(69.523)&\approx 1.2522\\ &\approx 71.69^{\circ} \end{align*}\]
O ângulo de elevação é de aproximadamente\(71.7°\) e o comprimento do cabo é de\(73.2\) metros.
Os regulamentos de segurança da OSHA exigem que a base de uma escada seja colocada a\(1\) pé da parede para cada\(4\) metro de comprimento da escada. Encontre o ângulo que uma escada de qualquer comprimento forma com o solo e a altura em que a escada toca a parede.
Solução
Para qualquer comprimento de escada, a base precisa estar a uma distância da parede igual a um quarto do comprimento da escada. Equivalentemente, se a base da escada estiver a “a” pés da parede, o comprimento da escada será de\(4a\) pés. Veja a Figura\(\PageIndex{5}\).
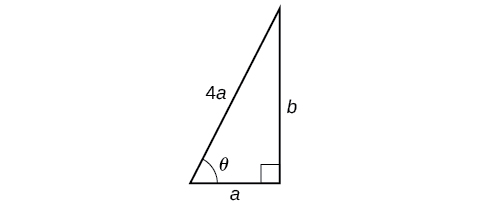
O lado adjacente ao\(\theta\) é\(a\) e a hipotenusa é\(4a\). Assim,
\[\begin{align*} \cos \theta&= \dfrac{a}{4a}\\ &= \dfrac{1}{4}\\ {\cos}^{-1}\left (\dfrac{1}{4}\right )&\approx 75.5^{\circ} \end{align*}\]
A elevação da escada forma um ângulo\(75.5°\) com o solo. A altura em que a escada toca a parede pode ser encontrada usando o Teorema de Pitágoras:
\[\begin{align*} a^2+b^2&= {(4a)}^2\\ b^2&= {(4a)}^2-a^2\\ b^2&= 16a^2-a^2\\ b^2&= 15a^2\\ b&= a\sqrt{15} \end{align*}\]
Assim, a escada toca a parede a\(a\sqrt{15}\) pés do chão.
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de equações trigonométricas.
- Resolvendo equações trigonométricas I
- Resolvendo equações trigonométricas II
- Resolvendo equações trigonométricas III
- Resolvendo equações trigonométricas IV
- Resolvendo equações trigonométricas V
- Resolvendo equações trigonométricas VI
Conceitos-chave
- Ao resolver equações trigonométricas lineares, podemos usar técnicas algébricas da mesma forma que fazemos para resolver equações algébricas. Procure padrões, como a diferença de quadrados, a forma quadrática ou uma expressão que se presta bem à substituição. Veja exemplo\(\PageIndex{1}\)\(\PageIndex{2}\), exemplo e exemplo\(\PageIndex{3}\).
- Equações envolvendo uma única função trigonométrica podem ser resolvidas ou verificadas usando o círculo unitário. Veja Exemplo\(\PageIndex{4}\)\(\PageIndex{5}\), Exemplo e Exemplo\(\PageIndex{6}\) e Exemplo\(\PageIndex{7}\).
- Também podemos resolver equações trigonométricas usando uma calculadora gráfica. Veja o exemplo\(\PageIndex{8}\) e o exemplo\(\PageIndex{9}\).
- Muitas equações parecem quadráticas na forma. Podemos usar a substituição para fazer com que a equação pareça mais simples e, em seguida, usar as mesmas técnicas que usamos para resolver uma quadrática algébrica: fatoração, fórmula quadrática etc. Veja Exemplo\(\PageIndex{10}\)\(\PageIndex{11}\), Exemplo\(\PageIndex{12}\), Exemplo e Exemplo\(\PageIndex{13}\).
- Também podemos usar as identidades para resolver a equação trigonométrica. Veja exemplo\(\PageIndex{14}\)\(\PageIndex{15}\), exemplo e exemplo\(\PageIndex{16}\).
- Podemos usar a substituição para resolver uma equação trigonométrica de múltiplos ângulos, que é a compressão de uma função trigonométrica padrão. Precisaremos levar em consideração a compressão e verificar se encontramos todas as soluções no intervalo determinado. Veja o exemplo\(\PageIndex{17}\).
- Cenários do mundo real podem ser modelados e resolvidos usando o Teorema de Pitágoras e funções trigonométricas. Veja o exemplo\(\PageIndex{18}\).


