5.1: Funções quadráticas
- Page ID
- 187074
Objetivos de
- Reconheça as características das parábolas.
- Entenda como o gráfico de uma parábola está relacionado à sua função quadrática.
- Determine o valor mínimo ou máximo de uma função quadrática.
- Resolva problemas envolvendo o valor mínimo ou máximo de uma função quadrática.
Antenas curvas, como as mostradas na Figura\(\PageIndex{1}\), são comumente usadas para focar microondas e ondas de rádio para transmitir sinais de televisão e telefone, bem como comunicação por satélite e naves espaciais. A seção transversal da antena tem a forma de uma parábola, que pode ser descrita por uma função quadrática.

Figura\(\PageIndex{1}\): Uma série de antenas parabólicas. (crédito: Matthew Colvin de Valle, Flickr)
Nesta seção, investigaremos funções quadráticas, que frequentemente modelam problemas envolvendo área e movimento de projéteis. Trabalhar com funções quadráticas pode ser menos complexo do que trabalhar com funções de alto grau, portanto, elas oferecem uma boa oportunidade para um estudo detalhado do comportamento da função.
Reconhecendo as características das parábolas
O gráfico de uma função quadrática é uma curva em forma de U chamada parábola. Uma característica importante do gráfico é que ele tem um ponto extremo, chamado vértice. Se a parábola se abrir, o vértice representa o ponto mais baixo do gráfico ou o valor mínimo da função quadrática. Se a parábola se abrir para baixo, o vértice representa o ponto mais alto do gráfico ou o valor máximo. Em ambos os casos, o vértice é um ponto de virada no gráfico. O gráfico também é simétrico com uma linha vertical desenhada através do vértice, chamada eixo de simetria. Esses recursos são ilustrados na Figura\(\PageIndex{2}\).

O intercepto y é o ponto em que a parábola cruza o\(y\) eixo y. Os interceptos x são os pontos nos quais a parábola cruza o\(x\) eixo. Se existirem, os interceptos x representam os zeros, ou raízes, da função quadrática, cujos valores\(y=0\).\(x\)
Exemplo\(\PageIndex{1}\): Identifying the Characteristics of a Parabola
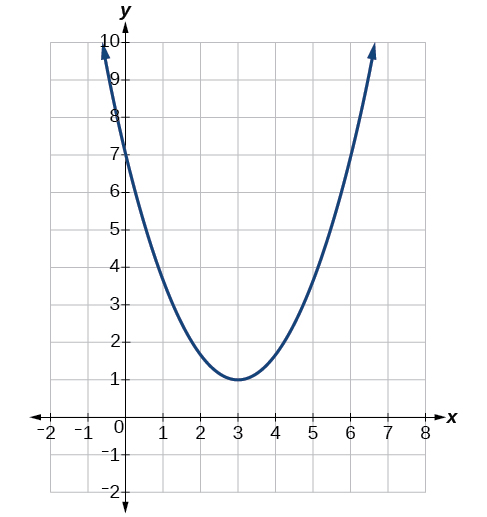
Determine o vértice, eixo de simetria, zeros e intercepto y da parábola mostrada na Figura\(\PageIndex{3}\).
Solução
O vértice é o ponto de virada do gráfico. Podemos ver que o vértice está em\((3,1)\). Como essa parábola se abre para cima, o eixo de simetria é a linha vertical que cruza a parábola no vértice. Então, o eixo de simetria é\(x=3\). Essa parábola não cruza o eixo x, então ela não tem zeros. Ele cruza o\(y\) eixo -em\((0,7)\), então esse é o intercepto y.
Entendendo como os gráficos das parábolas estão relacionados às suas funções quadráticas
A forma geral de uma função quadrática apresenta a função na forma
\[f(x)=ax^2+bx+c\]
onde\(a\)\(b\), e\(c\) são números reais\(a{\neq}0\) e. Se\(a>0\), a parábola se abre para cima. Se\(a<0\), a parábola se abre para baixo. Podemos usar a forma geral de uma parábola para encontrar a equação do eixo de simetria.
O eixo de simetria é definido por\(x=−\frac{b}{2a}\). Se usarmos a fórmula quadrática\(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\),,\(ax^2+bx+c=0\) para resolver os interceptos x, ou zeros, descobrimos que o valor da\(x\) metade entre eles é sempre\(x=−\frac{b}{2a}\), a equação para o eixo de simetria.
\(\PageIndex{4}\)A figura representa o gráfico da função quadrática escrito em forma geral como\(y=x^2+4x+3\). Neste formulário\(a=1\),\(b=4\),\(c=3\) e. Porque\(a>0\) a parábola se abre para cima. O eixo de simetria é\(x=−\frac{4}{2(1)}=−2\). Isso também faz sentido porque podemos ver no gráfico que a linha vertical\(x=−2\) divide o gráfico ao meio. O vértice sempre ocorre ao longo do eixo de simetria. Para uma parábola que se abre para cima, o vértice ocorre no ponto mais baixo do gráfico, neste caso,\((−2,−1)\). As interceptações x, aqueles pontos em que a parábola cruza o eixo x, ocorrem em\((−3,0)\)\((−1,0)\) e.
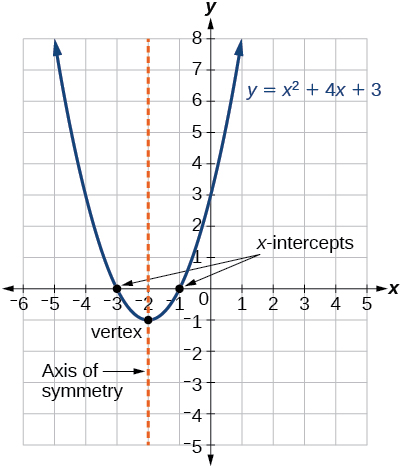
A forma padrão de uma função quadrática apresenta a função na forma
\[f(x)=a(x−h)^2+k\]
onde\((h, k)\) está o vértice. Como o vértice aparece na forma padrão da função quadrática, essa forma também é conhecida como forma de vértice de uma função quadrática.
Como na forma geral, if\(a>0\), a parábola se abre para cima e o vértice é mínimo. Se\(a<0\), a parábola se abre para baixo e o vértice é o máximo. \(\PageIndex{5}\)A figura representa o gráfico da função quadrática escrito na forma padrão como\(y=−3(x+2)^2+4\). Já que\(x–h=x+2\) neste exemplo,\(h=–2\). Neste formulário\(a=−3\),\(h=−2\),\(k=4\) e. Porque\(a<0\) a parábola se abre para baixo. O vértice está em\((−2, 4)\).
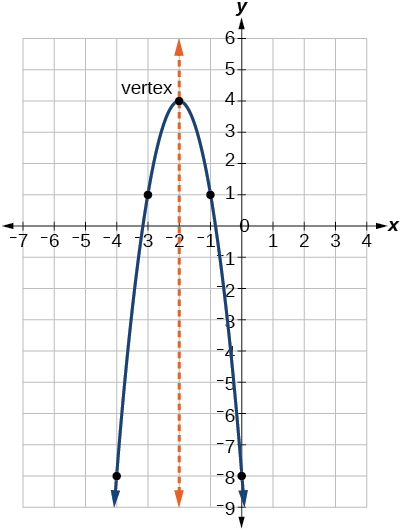
A forma padrão é útil para determinar como o gráfico é transformado a partir do gráfico de\(y=x^2\). A figura\(\PageIndex{6}\) é o gráfico dessa função básica.
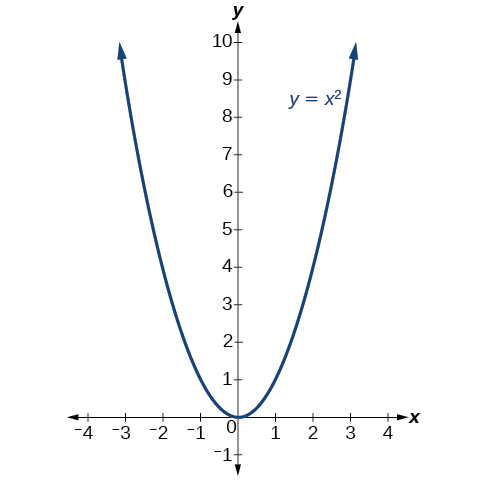
Se\(k>0\), o gráfico se desloca para cima, enquanto se\(k<0\), o gráfico se desloca para baixo. Na Figura\(\PageIndex{5}\),\(k>0\), então o gráfico é deslocado 4 unidades para cima. Se\(h>0\), o gráfico muda para a direita e se\(h<0\), o gráfico muda para a esquerda. Na Figura\(\PageIndex{5}\),\(h<0\), então o gráfico é deslocado 2 unidades para a esquerda. A magnitude de\(a\) indica a extensão do gráfico. Se\(|a|>1\), o ponto associado a um determinado valor de x se afasta mais do eixo x, então o gráfico parece ficar mais estreito e há um alongamento vertical. Mas se\(|a|<1\) o ponto associado a um determinado valor x se aproximar do eixo x, o gráfico parece ficar mais largo, mas na verdade há uma compressão vertical. Na Figura\(\PageIndex{5}\)\(|a|>1\), então o gráfico fica mais estreito.
A forma padrão e a forma geral são métodos equivalentes de descrever a mesma função. Podemos ver isso expandindo a forma geral e definindo-a como igual à forma padrão.
\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]
Para que os termos lineares sejam iguais, os coeficientes devem ser iguais.
\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]
Esse é o eixo de simetria que definimos anteriormente. Definindo os termos constantes como iguais:
\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]
Na prática, porém, geralmente é mais fácil lembrar que\(k\) é o valor de saída da função quando a entrada é\(h\), então\(f(h)=k\).
Definições: Formas de funções quadráticas
Uma função quadrática é uma função de grau dois. O gráfico de uma função quadrática é uma parábola.
- A forma geral de uma função quadrática é\(f(x)=ax^2+bx+c\) onde\(a\)\(b\), e\(c\) são números reais\(a{\neq}0\) e.
- A forma padrão de uma função quadrática é\(f(x)=a(x−h)^2+k\).
- O vértice\((h,k)\) está localizado em\[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]
COMO FAZER: Escreva uma função quadrática em uma forma geral
Dado um gráfico de uma função quadrática, escreva a equação da função na forma geral.
- Identifique o deslocamento horizontal da parábola; esse valor é\(h\). Identifique o deslocamento vertical da parábola; esse valor é\(k\).
- Substitua os valores do deslocamento horizontal\(h\) e vertical por\(k\) e. na função\(f(x)=a(x–h)^2+k\).
- Substitua os valores de qualquer ponto, exceto o vértice, no gráfico da parábola por\(x\)\(f(x)\) e.
- Resolva o fator de estiramento,\(|a|\).
- Se a parábola se abrir,\(a>0\). Se a parábola se abrir, isso significa\(a<0\) que o gráfico foi refletido sobre o eixo x.
- Expanda e simplifique para escrever de forma geral.
Exemplo\(\PageIndex{2}\): Writing the Equation of a Quadratic Function from the Graph
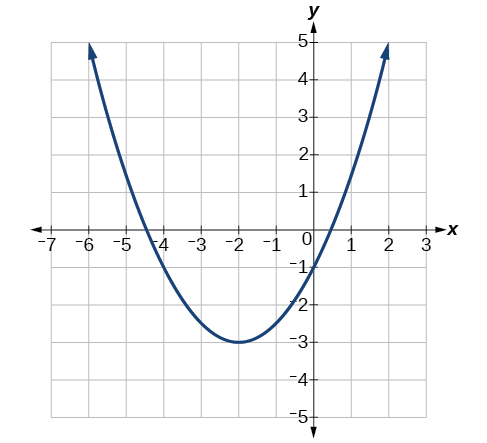
Escreva uma equação para a função quadrática\(g\) na Figura\(\PageIndex{7}\) como uma transformação de\(f(x)=x^2\), depois expanda a fórmula e simplifique os termos para escrever a equação na forma geral.
Solução
Podemos ver que o gráfico de\(g\) é o gráfico de\(f(x)=x^2\) deslocado para a esquerda 2 e para baixo 3, dando uma fórmula na forma\(g(x)=a(x+2)^2–3\).
Substituindo as coordenadas de um ponto na curva, por exemplo\((0,−1)\), podemos resolver o fator de estiramento.
\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]
Na forma padrão, o modelo algébrico para este gráfico é\(g(x)=\dfrac{1}{2}(x+2)^2–3\).
Para escrever isso na forma polinomial geral, podemos expandir a fórmula e simplificar os termos.
\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]
Observe que os deslocamentos horizontal e vertical do gráfico básico da função quadrática determinam a localização do vértice da parábola; o vértice não é afetado por alongamentos e compressões.
Análise
Podemos verificar nosso trabalho usando o recurso de tabela em um utilitário gráfico. Primeiro entre\(\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}\). Em seguida, selecione e\(\mathrm{TBLSET}\), em seguida\(\mathrm{ΔTbl = 2}\), use\(\mathrm{TblStart=–6}\) e e selecione\(\mathrm{TABLE}\). Veja a tabela\(\PageIndex{1}\)
| \(x\) | -6 | -4 | -2 | 0 | 2 |
|---|---|---|---|---|---|
| \(y\) | -5 | -1 | -3 | -1 | 5 |
Os pares ordenados na tabela correspondem aos pontos no gráfico.
Exercício\(\PageIndex{2}\)
Uma grade de coordenadas foi sobreposta ao caminho quadrático de uma bola de basquete na Figura\(\PageIndex{8}\). Encontre uma equação para o caminho da bola. O atirador faz a cesta?

Figura\(\PageIndex{8}\): Imagem em movimento de um garoto jogando uma bola de basquete em um aro para mostrar a curva parabólica que ela faz.
(crédito: modificação da obra de Dan Meyer)
- Responda
-
O caminho passa pela origem e tem vértice em\((−4, 7)\), então\(h(x)=–\frac{7}{16}(x+4)^2+7\). Para fazer o tiro,\(h(−7.5)\) precisaria ser cerca de 4, mas\(h(–7.5){\approx}1.64\); ele não consegue.
![]() Dada uma função quadrática na forma geral, encontre o vértice da parábola.
Dada uma função quadrática na forma geral, encontre o vértice da parábola.
- Identifique\(a\)\(b\),\(c\) e.
- Encontre\(h\) a coordenada x do vértice substituindo\(a\) e\(b\) em\(h=–\frac{b}{2a}\).
- Encontre\(k\) a coordenada y do vértice, avaliando\(k=f(h)=f\Big(−\frac{b}{2a}\Big)\).
Exemplo\(\PageIndex{3}\): Finding the Vertex of a Quadratic Function
Encontre o vértice da função quadrática\(f(x)=2x^2–6x+7\). Reescreva a quadrática na forma padrão (forma de vértice).
Solução
A coordenada horizontal do vértice estará em
\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]
A coordenada vertical do vértice estará em
\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]
Reescrevendo na forma padrão, o fator de estiramento será o\(a\) mesmo da quadrática original.
\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]
Usando o vértice para determinar os deslocamentos,
\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]
Análise
Uma razão pela qual podemos querer identificar o vértice da parábola é que esse ponto nos informará qual é o valor máximo ou mínimo da função e onde ela ocorre\((h)\).\((k)\)
Exercício\(\PageIndex{3}\)
Dada a equação\(g(x)=13+x^2−6x\), escreva a equação na forma geral e depois na forma padrão.
- Responda
-
\(g(x)=x^2−6x+13\)na forma geral;\(g(x)=(x−3)^2+4\) na forma padrão.
Encontrando o domínio e o alcance de uma função quadrática
Qualquer número pode ser o valor de entrada de uma função quadrática. Portanto, o domínio de qualquer função quadrática são todos números reais. Como as parábolas têm um ponto máximo ou mínimo, o alcance é restrito. Como o vértice de uma parábola será máximo ou mínimo, o intervalo consistirá em todos os valores y maiores ou iguais à coordenada y no ponto de virada ou menores ou iguais à coordenada y no ponto de virada, dependendo se a parábola se abre para cima ou para baixo.
Definição: Domínio e alcance de uma função quadrática
O domínio de qualquer função quadrática são todos números reais.
O intervalo de uma função quadrática escrita de forma geral\(f(x)=ax^2+bx+c\) com um\(a\) valor positivo é\(f(x){\geq}f ( −\frac{b}{2a}\Big)\), ou\([ f(−\frac{b}{2a}),∞ ) \); o intervalo de uma função quadrática escrita em forma geral com um valor negativo é\(f(x) \leq f(−\frac{b}{2a})\), ou\((−∞,f(−\frac{b}{2a})]\).
O intervalo de uma função quadrática escrita na forma padrão\(f(x)=a(x−h)^2+k\) com um\(a\) valor positivo é\(f(x) \geq k;\) o intervalo de uma função quadrática escrita na forma padrão com um\(a\) valor negativo é\(f(x) \leq k\).
![]() Dada uma função quadrática, encontre o domínio e o intervalo.
Dada uma função quadrática, encontre o domínio e o intervalo.
- Identifique o domínio de qualquer função quadrática como todos os números reais.
- Determine se\(a\) é positivo ou negativo. Se\(a\) for positivo, a parábola tem um mínimo. Se\(a\) for negativo, a parábola tem um máximo.
- Determine o valor máximo ou mínimo da parábola,\(k\).
- Se a parábola tiver um mínimo, o intervalo será dado por\(f(x){\geq}k\), ou\(\left[k,\infty\right)\). Se a parábola tiver um máximo, o intervalo será dado por\(f(x){\leq}k\), ou\(\left(−\infty,k\right]\).
Exemplo\(\PageIndex{4}\): Finding the Domain and Range of a Quadratic Function
Encontre o domínio e a variedade de\(f(x)=−5x^2+9x−1\).
Solução
Como acontece com qualquer função quadrática, o domínio é todo números reais.
Como\(a\) é negativa, a parábola se abre para baixo e tem um valor máximo. Precisamos determinar o valor máximo. Podemos começar encontrando o valor x do vértice.
\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]
O valor máximo é dado por\(f(h)\).
\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]
O alcance é\(f(x){\leq}\frac{61}{20}\), ou\(\left(−\infty,\frac{61}{20}\right]\).
Exercício\(\PageIndex{4}\)
Encontre o domínio e a variedade de\(f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}\).
- Responda
-
O domínio é todo em números reais. O alcance é\(f(x){\geq}\frac{8}{11}\), ou\(\left[\frac{8}{11},\infty\right)\).
Determinando os valores máximo e mínimo de funções quadráticas
A saída da função quadrática no vértice é o valor máximo ou mínimo da função, dependendo da orientação da parábola. Podemos ver os valores máximo e mínimo na Figura\(\PageIndex{9}\).
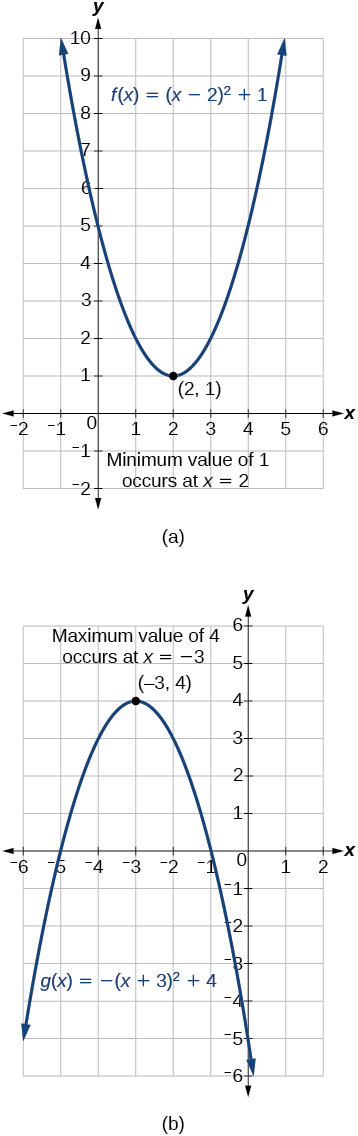
Há muitos cenários reais que envolvem encontrar o valor máximo ou mínimo de uma função quadrática, como aplicativos que envolvem área e receita.
Exemplo\(\PageIndex{5}\): Finding the Maximum Value of a Quadratic Function
Uma agricultora de quintal quer cercar um espaço retangular para um novo jardim dentro de seu quintal cercado. Ela comprou 80 pés de cerca de arame para cercar três lados e usará uma seção da cerca do quintal como o quarto lado.
- Encontre uma fórmula para a área delimitada pela cerca se os lados da cerca perpendiculares à cerca existente tiverem comprimento\(L\).
- Quais dimensões ela deve fazer em seu jardim para maximizar a área fechada?
Solução
Vamos usar um diagrama como Figura\(\PageIndex{10}\) para registrar as informações fornecidas. Também é útil introduzir uma variável temporária,\(W\), para representar a largura do jardim e o comprimento da seção da cerca paralela à cerca do quintal.
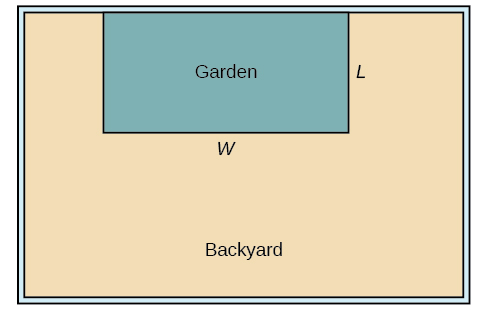
a. Sabemos que temos apenas 80 pés de cerca disponíveis e\(L+W+L=80\), ou mais simplesmente,\(2L+W=80\). Isso nos permite representar a largura,\(W\), em termos de\(L\).
\[W=80−2L\]
Agora estamos prontos para escrever uma equação para a área que a cerca envolve. Sabemos que a área de um retângulo é o comprimento multiplicado pela largura, então
\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]
Essa fórmula representa a área da cerca em termos do comprimento variável\(L\). A função, escrita de forma geral, é
\[A(L)=−2L^2+80L\].
A quadrática tem um coeficiente inicial negativo, então o gráfico se abrirá para baixo e o vértice será o valor máximo para a área. Ao encontrar o vértice, devemos ter cuidado porque a equação não está escrita na forma polinomial padrão com potências decrescentes. É por isso que reescrevemos a função na forma geral acima. Uma vez que\(a\) é o coeficiente do termo quadrado\(a=−2\)\(b=80\),,\(c=0\) e.
Para encontrar o vértice:
\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]
O valor máximo da função é uma área de 800 pés quadrados, que ocorre quando\(L=20\) pés. Quando os lados mais curtos têm 20 pés, restam 40 pés de cerca para o lado mais longo. Para maximizar a área, ela deve cercar o jardim de forma que os dois lados mais curtos tenham 20 pés de comprimento e o lado mais longo paralelo à cerca existente tenha 40 pés de comprimento.
Análise
Esse problema também pode ser resolvido representando graficamente a função quadrática. Podemos ver onde a área máxima ocorre em um gráfico da função quadrática na Figura\(\PageIndex{11}\).
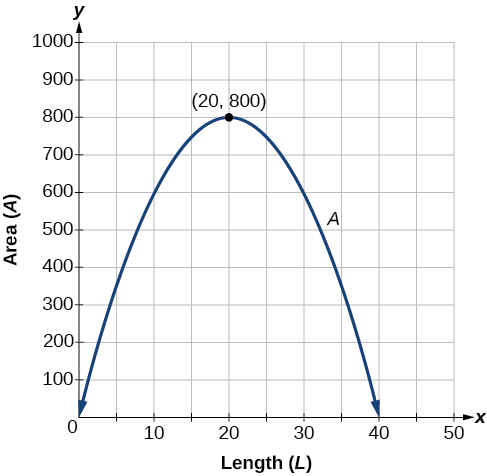
![]() Dada uma aplicação que envolve receita, use uma equação quadrática para encontrar o máximo.
Dada uma aplicação que envolve receita, use uma equação quadrática para encontrar o máximo.
- Escreva uma equação quadrática para receita.
- Encontre o vértice da equação quadrática.
- Determine o valor y do vértice.
Exemplo\(\PageIndex{6}\): Finding Maximum Revenue
O preço unitário de um item afeta sua oferta e demanda. Ou seja, se o preço unitário subir, a demanda pelo item geralmente diminuirá. Por exemplo, um jornal local atualmente tem 84.000 assinantes com uma taxa trimestral de $30. Pesquisas de mercado sugeriram que, se os proprietários aumentassem o preço para $32, perderiam 5.000 assinantes. Supondo que as assinaturas estejam linearmente relacionadas ao preço, qual preço o jornal deve cobrar por uma assinatura trimestral para maximizar sua receita?
Solução
A receita é a quantidade de dinheiro que uma empresa gera. Nesse caso, a receita pode ser encontrada multiplicando o preço por assinatura pelo número de assinantes ou pela quantidade. Podemos introduzir variáveis,\(p\) para preço por assinatura e\(Q\) quantidade, fornecendo a equação\(\text{Revenue}=pQ\).
Como o número de assinantes muda com o preço, precisamos encontrar uma relação entre as variáveis. Sabemos disso atualmente\(p=30\)\(Q=84,000\) e. Também sabemos que se o preço subir para $32, o jornal perderia 5.000 assinantes, dando um segundo par de valores,\(p=32\)\(Q=79,000\) e. A partir disso, podemos encontrar uma equação linear relacionando as duas quantidades. A inclinação será
\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]
Isso nos diz que o jornal perderá 2.500 assinantes por cada dólar que aumentar o preço. Podemos então resolver o intercepto y.
\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]
Isso nos dá a equação linear que\(Q=−2,500p+159,000\) relaciona custo e assinantes. Agora retornamos à nossa equação de receita.
\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]
Agora temos uma função quadrática de receita em função da taxa de assinatura. Para encontrar o preço que maximizará a receita do jornal, podemos encontrar o vértice.
\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]
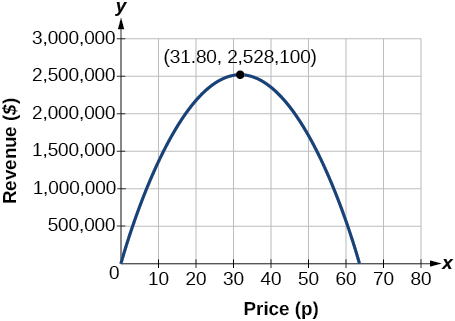
O modelo nos diz que a receita máxima ocorrerá se o jornal cobrar $31,80 por uma assinatura. Para descobrir qual é a receita máxima, avaliamos a função de receita.
\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]
Análise
Isso também pode ser resolvido representando graficamente a quadrática, como na Figura\(\PageIndex{12}\). Podemos ver a receita máxima em um gráfico da função quadrática.
Encontrando os interceptos x e Y de uma função quadrática
Assim como fizemos nos problemas de aplicação acima, também precisamos encontrar interceptações de equações quadráticas para representar graficamente parábolas. Lembre-se de que encontramos o intercepto y de uma quadrática avaliando a função em uma entrada de zero e encontramos os interceptos x em locais onde a saída é zero. Observe na Figura\(\PageIndex{13}\) que o número de interceptações x pode variar dependendo da localização do gráfico.

![]() Dada uma função quadrática\(f(x)\), encontre os interceptos y e x.
Dada uma função quadrática\(f(x)\), encontre os interceptos y e x.
- Avalie\(f(0)\) para encontrar o intercepto y.
- Resolva a equação quadrática\(f(x)=0\) para encontrar os interceptos x.
Exemplo\(\PageIndex{7}\): Finding the y- and x-Intercepts of a Parabola
Encontre as interceptações y e x da quadrática\(f(x)=3x^2+5x−2\).
Solução
Encontramos o intercepto y avaliando\(f(0)\).
\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]
Então, o intercepto y está em\((0,−2)\).
Para os interceptos x, encontramos todas as soluções de\(f(x)=0\).
\[0=3x^2+5x−2\]
Nesse caso, a quadrática pode ser fatorada facilmente, fornecendo o método mais simples de solução.
\[0=(3x−1)(x+2)\]
\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]
Então, as interceptações x estão em\((\frac{1}{3},0)\)\((−2,0)\) e.
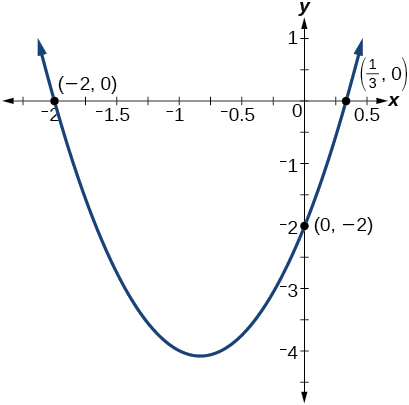
Análise
Ao representar graficamente a função, podemos confirmar que o gráfico cruza o\(y\) eixo -em\((0,−2)\). Também podemos confirmar que o gráfico cruza o eixo x em\(\Big(\frac{1}{3},0\Big)\)\((−2,0)\) e. Veja a Figura\(\PageIndex{14}\).
Reescrevendo quadráticas em formato padrão
No exemplo\(\PageIndex{7}\), a quadrática foi facilmente resolvida por fatoração. No entanto, existem muitas equações quadráticas que não podem ser fatoradas. Podemos resolver essas equações quadráticas reescrevendo-as primeiro na forma padrão.
![]() Dada uma função quadrática, encontre os interceptos x reescrevendo na forma padrão.
Dada uma função quadrática, encontre os interceptos x reescrevendo na forma padrão.
- Substitua um e\(b\) em\(h=−\frac{b}{2a}\).
- Substitua\(x=h\) na forma geral da função quadrática para encontrar\(k\).
- Reescreva a quadrática na forma padrão usando\(h\)\(k\) e.
- Resolva quando a saída da função será zero para encontrar os interceptos x.
Exemplo\(\PageIndex{8}\): Finding the x-Intercepts of a Parabola
Encontre os interceptos x da função quadrática\(f(x)=2x^2+4x−4\).
Solução
Começamos resolvendo quando a saída será zero.
\[0=2x^2+4x−4 \nonumber\]
Como a quadrática não é facilmente fatorável nesse caso, resolvemos as interceptações primeiro reescrevendo a quadrática na forma padrão.
\[f(x)=a(x−h)^2+k\nonumber\]
Nós sabemos disso\(a=2\). Em seguida, resolvemos para\(h\)\(k\) e.
\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]
Então, agora podemos reescrever na forma padrão.
\[f(x)=2(x+1)^2−6\nonumber\]
Agora podemos resolver quando a saída será zero.
\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]
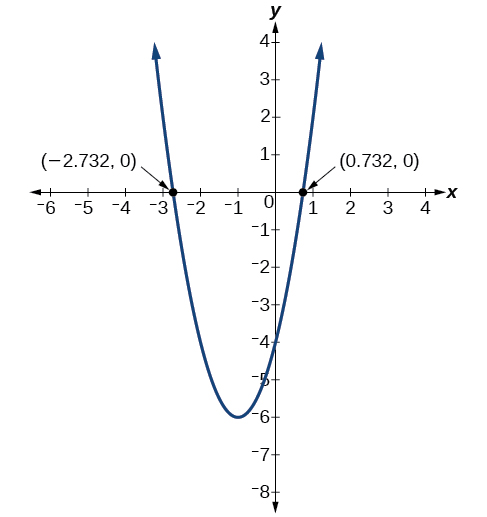
O gráfico tem interceptações x em\((−1−\sqrt{3},0)\)\((−1+\sqrt{3},0)\) e.
Análise
Podemos verificar nosso trabalho representando graficamente a função dada em um utilitário gráfico e observando os interceptos x. Veja a Figura\(\PageIndex{15}\).
Exercício\(\PageIndex{1}\)
Em Try It\(\PageIndex{1}\), encontramos a forma padrão e geral da função\(g(x)=13+x^2−6x\). Agora encontre as interceptações y e x (se houver).
- Responda
-
intercepto y em\((0, 13)\), sem interceptações x
Exemplo\(\PageIndex{9}\): Solving a Quadratic Equation with the Quadratic Formula
Resolver\(x^2+x+2=0\).
Solução
Vamos começar escrevendo a fórmula quadrática:\(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\).
Ao aplicar a fórmula quadrática, identificamos os coeficientes\(a\)\(b\)\(c\) e. Para a equação\(x^2+x+2=0\)\(a=1\), temos\(b=1\),\(c=2\) e. Substituindo esses valores na fórmula, temos:
\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]
As soluções para a equação são\(x=\frac{−1+i\sqrt{7}}{2}\)\(x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}\) e\(x=\frac{−1-i\sqrt{7}}{2}\) ou\(x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}\) e.
Exemplo\(\PageIndex{10}\): Applying the Vertex and x-Intercepts of a Parabola
Uma bola é lançada para cima do topo de um prédio de 40 pés de altura a uma velocidade de 80 pés por segundo. A altura da bola acima do solo pode ser modelada pela equação\(H(t)=−16t^2+80t+40\).
Quando a bola atinge a altura máxima?
Qual é a altura máxima da bola?
Quando a bola cai no chão?
A bola atinge a altura máxima no vértice da parábola.
\[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]
A bola atinge a altura máxima após 2,5 segundos.
Para encontrar a altura máxima, encontre a coordenada y do vértice da parábola.
\[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]
A bola atinge uma altura máxima de 140 pés.
Para descobrir quando a bola atinge o chão, precisamos determinar quando a altura é zero\(H(t)=0\).
Usamos a fórmula quadrática.
\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]
Como a raiz quadrada não simplifica muito bem, podemos usar uma calculadora para aproximar os valores das soluções.
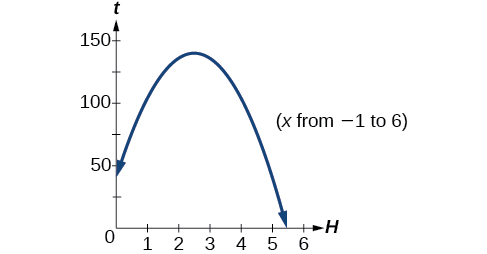
\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]
A segunda resposta está fora do domínio razoável do nosso modelo, então concluímos que a bola atingirá o chão após cerca de 5.458 segundos. Veja a Figura\(\PageIndex{16}\).
![]() \(\PageIndex{5}\): Uma rocha é lançada para cima do topo de um penhasco de 112 pés de altura com vista para o oceano a uma velocidade de 96 pés por segundo. A altura da rocha acima do oceano pode ser modelada pela equação\(H(t)=−16t^2+96t+112\).
\(\PageIndex{5}\): Uma rocha é lançada para cima do topo de um penhasco de 112 pés de altura com vista para o oceano a uma velocidade de 96 pés por segundo. A altura da rocha acima do oceano pode ser modelada pela equação\(H(t)=−16t^2+96t+112\).
- Quando a rocha atinge a altura máxima?
- Qual é a altura máxima da rocha?
- Quando a rocha atinge o oceano?
Solução
a. 3 segundos b. 256 pés c. 7 segundos
Equações chave
- forma geral de uma função quadrática:\(f(x)=ax^2+bx+c\)
- a fórmula quadrática:\(x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}\)
- forma padrão de uma função quadrática:\(f(x)=a(x−h)^2+k\)
Conceitos chave
- Uma função polinomial de grau dois é chamada de função quadrática.
- O gráfico de uma função quadrática é uma parábola. Uma parábola é uma curva em forma de U que pode se abrir para cima ou para baixo.
- O eixo de simetria é a linha vertical que passa pelo vértice. Os zeros, ou interceptos x, são os pontos nos quais a parábola cruza o eixo x. O intercepto y é o ponto em que a parábola cruza o\(y\) eixo y.
- As funções quadráticas geralmente são escritas de forma geral. A forma padrão ou de vértice é útil para identificar facilmente o vértice de uma parábola. Qualquer formulário pode ser escrito a partir de um gráfico.
- O vértice pode ser encontrado a partir de uma equação representando uma função quadrática.
- O domínio de uma função quadrática são todos números reais. O intervalo varia com a função.
- O valor mínimo ou máximo de uma função quadrática é dado pelo valor y do vértice.
- O valor mínimo ou máximo de uma função quadrática pode ser usado para determinar o alcance da função e resolver muitos tipos de problemas do mundo real, incluindo problemas envolvendo área e receita.
- Algumas equações quadráticas devem ser resolvidas usando a fórmula quadrática.
- O vértice e as interceptações podem ser identificados e interpretados para resolver problemas do mundo real.
Glossário
eixo de simetria
uma linha vertical traçada através do vértice de uma parábola em torno da qual a parábola é simétrica; ela é definida por\(x=−\frac{b}{2a}\).
forma geral de uma função quadrática
a função que descreve uma parábola, escrita na forma\(f(x)=ax^2+bx+c\), onde\(a,b,\) e\(c\) são números reais e a≠ 0.
forma padrão de uma função quadrática
a função que descreve uma parábola, escrita na forma\(f(x)=a(x−h)^2+k\), onde\((h, k)\) está o vértice.
vértice
o ponto em que uma parábola muda de direção, correspondendo ao valor mínimo ou máximo da função quadrática
forma de vértice de uma função quadrática
outro nome para a forma padrão de uma função quadrática
zeros
em uma determinada função, cujos valores\(y=0\), também chamados de\(x\) raízes


