3.6: Funções de valor absoluto
- Page ID
- 187007
Objetivos de
- Representar graficamente uma função de valor ab
- Resolva uma equação de valor absoluto.
Até a década de 1920, acreditava-se que as chamadas nebulosas espirais eram nuvens de poeira e gás em nossa própria galáxia, a cerca de dezenas de milhares de anos-luz de distância. Então, o astrônomo Edwin Hubble provou que esses objetos são galáxias por si só, a distâncias de milhões de anos-luz. Hoje, os astrônomos podem detectar galáxias que estão a bilhões de anos-luz de distância. As distâncias no universo podem ser medidas em todas as direções. Como tal, é útil considerar a distância como uma função de valor absoluto. Nesta seção, investigaremos funções de valor absoluto.

Entendendo o valor ab
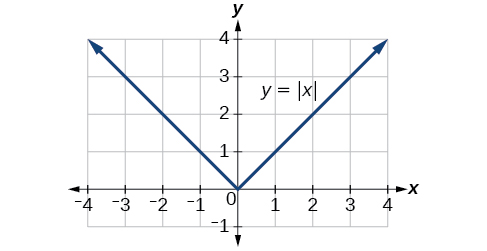
Lembre-se de que, em sua forma básica\(f(x)=|x|\), a função de valor absoluto é uma das funções do nosso kit de ferramentas. A função de valor absoluto é comumente considerada como fornecendo a distância entre o número e zero em uma reta numérica. Algebricamente, para qualquer que seja o valor de entrada, a saída é o valor sem levar em conta o sinal.
Função de valor absoluto
A função de valor absoluto pode ser definida como uma função por partes.
\[f(x)=|x|= \begin{cases} x & \text{ if }x{\geq}0 \\ -x & \text{ if } x<0 \end{cases}\]
Exemplo\(\PageIndex{1}\): Determine a Number within a Prescribed Distance
Descreva todos os valores\(x\) dentro ou incluindo uma distância de 4 do número 5.
Solução
Queremos que a distância entre\(x\) e 5 seja menor ou igual a 4. Podemos desenhar uma reta numérica, como a que está em, para representar a condição a ser satisfeita.

A distância de\(x\) até 5 pode ser representada usando o valor absoluto como\(|x−5|\). Queremos que os valores\(x\) que satisfaçam a condição\(| x−5 |\leq4\).
Análise
Note que
\[\begin{align*} -4&{\leq}x-5 & x-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
Então\(|x−5|\leq4\) é equivalente\(1{\leq}x\leq9\) a.
No entanto, os matemáticos geralmente preferem a notação de valor absoluto.
Exercício\(\PageIndex{1}\)
Descreva todos os valores a uma\(x\) distância de 3 do número 2.
- Responda
-
\(|x−2|\leq3\)
Exemplo\(\PageIndex{2}\): Resistance of a Resistor
As peças elétricas, como resistores e capacitores, vêm com valores específicos de seus parâmetros operacionais: resistência, capacitância, etc. No entanto, devido à imprecisão na fabricação, os valores reais desses parâmetros variam um pouco de peça para peça, mesmo quando deveriam ser os mesmos. O melhor que os fabricantes podem fazer é tentar garantir que as variações permaneçam dentro de uma faixa especificada, geralmente ± 1%, ± 5% ou ± 10%.
Suponha que tenhamos um resistor avaliado em 680 ohms, ± 5%. Use a função de valor absoluto para expressar a faixa de valores possíveis da resistência real.
Solução
5% dos 680 ohms são 34 ohms. O valor absoluto da diferença entre a resistência real e nominal não deve exceder a variabilidade declarada, portanto, com a resistência\(R\) em ohms,
\[|R−680|\leq34 \nonumber\]
Exercício\(\PageIndex{2}\)
Os estudantes que obtiverem uma pontuação de até 20 pontos de 80 passarão em um teste. Escreva isso como uma distância de 80 usando a notação de valor absoluto.
- Responda
-
Usando a variável\(p\) para passar,\(| p−80 |\leq20\)
Gráfico de uma função de valor absoluto
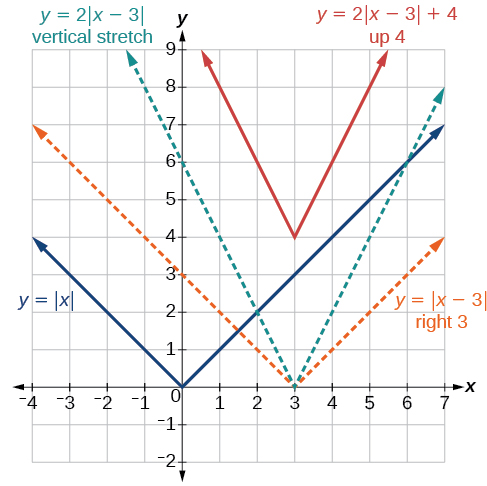
A característica mais significativa do gráfico de valor absoluto é o ponto angular no qual o gráfico muda de direção. Este ponto é mostrado na origem na Figura\(\PageIndex{3}\).
A figura\(\PageIndex{3}\) mostra o gráfico de\(y=2|x–3|+4\). O gráfico de\(y=|x|\) foi deslocado para a direita 3 unidades, esticado verticalmente por um fator de 2 e deslocado para cima 4 unidades. Isso significa que o ponto angular está localizado em\((3,4)\) para essa função transformada.
Exemplo\(\PageIndex{3}\): Writing an Equation for an Absolute Value Function
Escreva uma equação para a função representada graficamente na Figura\(\PageIndex{5}\).
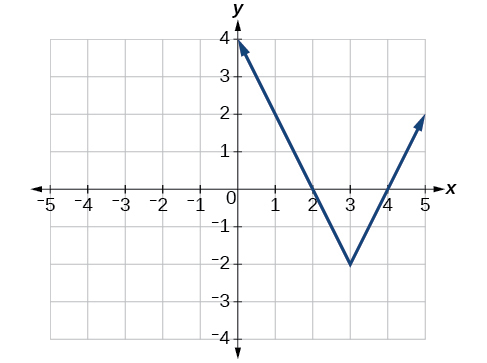
Solução
A função básica de valor absoluto muda de direção na origem, então esse gráfico foi deslocado para a direita 3 unidades e para baixo 2 unidades da função básica do kit de ferramentas. Veja a Figura\(\PageIndex{6}\).
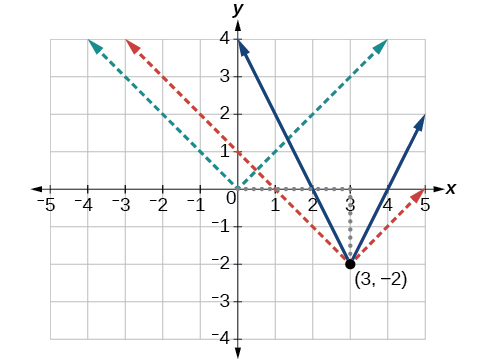
Também notamos que o gráfico parece esticado verticalmente, porque a largura do gráfico final em uma linha horizontal não é igual a 2 vezes a distância vertical do canto até essa linha, como seria para uma função de valor absoluto não esticada. Em vez disso, a largura é igual a 1 vez a distância vertical, conforme mostrado na Figura\(\PageIndex{7}\).
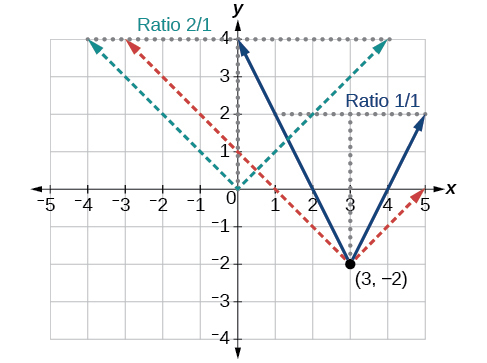
A partir dessas informações, podemos escrever a equação
\[\begin{align*} f(x)&=2|x-3|-2, \;\;\;\;\;\; \text{treating the stretch as a vertial stretch, or} \\ f(x)&=|2(x-3)|-2, \;\;\; \text{treating the stretch as a horizontal compression.} \end{align*}\]
Análise
Observe que essas equações são algebricamente equivalentes — o alongamento de uma função de valor absoluto pode ser escrito de forma intercambiável como alongamento ou compressão vertical ou horizontal.
PERGUNTAS E RESPOSTAS
Se não pudéssemos observar a extensão da função a partir dos gráficos, poderíamos determiná-la algebricamente?
- Responda
-
Sim. Se não conseguirmos determinar a extensão com base na largura do gráfico, podemos resolver o fator de estiramento colocando um par conhecido de valores para\(x\)\(f(x)\) e.
\[f(x)=a|x−3|−2 \nonumber\]
Agora substituindo o ponto\((1, 2)\)
\[\begin{align*} 2&=a|1-3|-2 \\ 4&=2a \\ a&=2 \end{align*}\]
Exercício\(\PageIndex{3}\)
Escreva a equação para a função de valor absoluto que é deslocada horizontalmente para a esquerda em 2 unidades, é invertida verticalmente e deslocada verticalmente para cima 3 unidades.
- Responda
-
\(f(x)=−| x+2 |+3\)
PERGUNTAS E RESPOSTAS
Os gráficos das funções de valor absoluto sempre cruzam o eixo vertical? O eixo horizontal?
- Responda
-
Sim, eles sempre cruzam o eixo vertical. O gráfico de uma função de valor absoluto cruzará o eixo vertical quando a entrada for zero.
Não, eles nem sempre cruzam o eixo horizontal. O gráfico pode ou não cruzar o eixo horizontal, dependendo de como o gráfico foi deslocado e refletido. É possível que a função de valor absoluto cruze o eixo horizontal em zero, um ou dois pontos (Figura\(\PageIndex{8}\)).
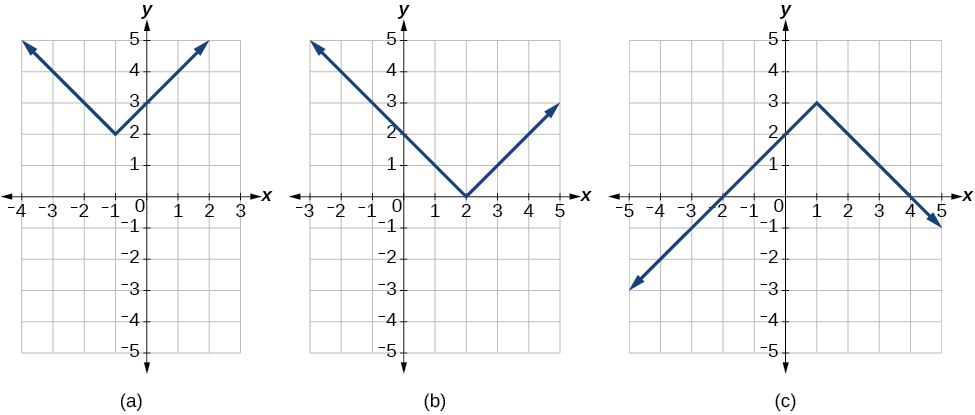
Figura\(\PageIndex{8}\): (a) A função de valor absoluto não cruza o eixo horizontal. (b) A função de valor absoluto cruza o eixo horizontal em um ponto. (c) A função de valor absoluto cruza o eixo horizontal em dois pontos.
Resolvendo uma equação de valor absoluto
Agora que podemos representar graficamente uma função de valor absoluto, aprenderemos como resolver uma equação de valor absoluto. Para resolver uma equação como\(8=|2x−6|\), notamos que o valor absoluto será igual a 8 se a quantidade dentro do valor absoluto for 8 ou -8. Isso leva a duas equações diferentes que podemos resolver de forma independente.
\[2x-6=8 \quad \text{ or } \quad 2x-6=-8 \nonumber\]
\[\begin{align*} 2x &= 14 & 2x &= -2 \\ x&=7 & x&=-1 \end{align*}\]
Saber como resolver problemas envolvendo funções de valor absoluto é útil. Por exemplo, talvez precisemos identificar números ou pontos em uma linha que estão a uma distância especificada de um determinado ponto de referência.
Uma equação de valor absoluto é uma equação na qual a variável desconhecida aparece em barras de valor absoluto. Por exemplo,
\[\begin{align*}|x|&=4, \nonumber \\[4pt] |2x−1| &=3, \\[4pt] |5x+2|−4 &=9. \end{align*}\]
Soluções para equações de valor absoluto
Para números reais\(A\) e\(B\), uma equação da forma\(|A|=B\), com\(B\geq0\), terá soluções quando\(A=B\) ou\(A=−B\). Se\(B<0\), a equação não\(|A|=B\) tem solução.
Como fazer...
Dada a fórmula para uma função de valor absoluto, encontre as interceptações horizontais de seu gráfico.
- Isole o termo de valor absoluto.
- Use\(|A|=B\) para escrever\(A=B\) ou\(−A=B\), supondo que\(B>0\).
- Resolva para\(x\).
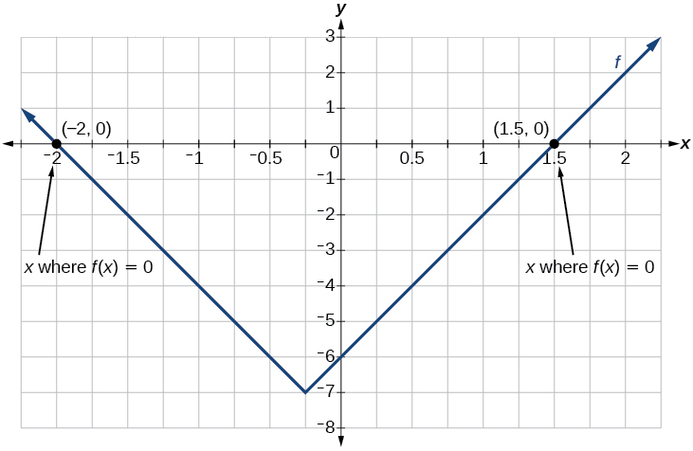
Exemplo\(\PageIndex{4}\): Finding the Zeros of an Absolute Value Function
Para a função\(f(x)=|4x+1|−7\), encontre os valores de\(x\) tal que\(f(x)=0\).
Solução
\[\begin{align*} 0&=|4x+1|-7 & & &\text{Substitute 0 for f(x).} \\ 7&=|4x+1| & & &\text{Isolate the absolute value on one side of the equation.} \\ 7&=4x+1 &\text{or} -7&=4x+1 &\text{Break into two separate equations and solve.} \\ 6&=4x & -8&=4x & \\ x&=\frac{6}{4}=1.5 & x&=\frac{-8}{4}=-2 \end{align*}\]
A função gera 0 quando\(x=1.5\) ou\(x=−2\) (Figura\(\PageIndex{9}\)).
Exercício\(\PageIndex{4}\)
Para a função\(f(x)=|2x−1|−3\), encontre os valores de\(x\) tal que\(f(x)=0\).
Solução
\(x=−1\)ou\(x=2\)
PERGUNTAS E RESPOSTAS
Devemos sempre esperar duas respostas ao resolver\(|A|=B\)?
Responda
Não. Podemos encontrar uma, duas ou até mesmo nenhuma resposta. Por exemplo, não há solução para\(2+|3x−5|=1\).
Como fazer...
Dada uma equação de valor absoluto, resolva-a.
- Isole o termo de valor absoluto.
- Use\(|A|=B\) para escrever\(A=B\) ou\(A=−B\).
- Resolva para\(x\).
Exemplo\(\PageIndex{5}\): Solving an Absolute Value Equation
Resolver\(1=4|x−2|+2\).
Solução
Isolar o valor absoluto em um lado da equação fornece o seguinte.
\[\begin{align*} 1&=4|x-2|+2 \\ -1&=4|x-2| \\ -\frac{1}{4}&=|x-2| \end{align*}\]
O valor absoluto sempre retorna um valor positivo, portanto, é impossível que o valor absoluto seja igual a um valor negativo. Nesse ponto, notamos que essa equação não tem soluções.
PERGUNTAS E RESPOSTAS
No exemplo\(\PageIndex{5}\), se\(f(x)=1\) e\(g(x)=4|x−2|+2\) fossem representados graficamente no mesmo conjunto de eixos, os gráficos se cruzariam?
Responda
Não. Os gráficos de\(f\) e não se\(g\) cruzariam, conforme mostrado na Figura\(\PageIndex{10}\). Isso confirma, graficamente, que a equação não\(1=4|x−2|+2\) tem solução.
Descubra onde o gráfico da função\(f(x)=−| x+2 |+3\) cruza os eixos horizontal e vertical.
\(f(0)=1\), então o gráfico cruza o eixo vertical em\((0,1)\). \(f(x)=0\)quando\(x=−5\) e\(x=1\) assim o gráfico cruza o eixo horizontal em\((−5,0)\)\((1,0)\) e.
Resolvendo uma desigualdade de valor absoluto
Equações de valor absoluto nem sempre envolvem igualdades. Em vez disso, talvez precisemos resolver uma equação dentro de uma faixa de valores. Nós usaríamos uma desigualdade de valor absoluto para resolver tal equação. Uma desigualdade de valor absoluto é uma equação da forma
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
ou
\[ |A|{\geq}B, \nonumber\]
onde uma expressão\(A\) (e possivelmente, mas não normalmente\(B\)) depende de uma variável\(x\). Resolver a desigualdade significa encontrar o conjunto de todos os\(x\) que satisfazem a desigualdade. Normalmente, esse conjunto será um intervalo ou a união de dois intervalos.
Existem duas abordagens básicas para resolver desigualdades de valor absoluto: gráfica e algébrica. A vantagem da abordagem gráfica é que podemos ler a solução interpretando os gráficos de duas funções. A vantagem da abordagem algébrica é que ela produz soluções que podem ser difíceis de ler no gráfico.
Por exemplo, sabemos que todos os números dentro de 200 unidades de 0 podem ser expressos como
\[|x|<200 \nonumber\]
ou
\[ −200<x<200 \nonumber\]
Suponha que queiramos saber todos os retornos possíveis de um investimento se pudermos ganhar alguma quantia de dinheiro entre $200 e $600. Podemos resolver algebricamente o conjunto de valores de\(x\) forma que a distância entre\(x\) e 600 seja menor que 200. Representamos a distância entre\(x\) e 600\(|x−600|\) a.
\[|x−600|<200\]
ou
\[−200<x−600<200\]
\[\begin{align*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \end{align*}\]
Isso significa que nossos retornos seriam entre $400 e $800.
Às vezes, um problema de desigualdade de valor absoluto nos será apresentado em termos de uma função de valor absoluto deslocada e/ou esticada ou comprimida, onde devemos determinar para quais valores da entrada a saída da função será negativa ou positiva.
Como fazer...
Dada uma desigualdade de valor absoluto da forma\(|x−A|{\leq}B\) para números reais\(a\) e\(b\) onde\(b\) é positiva, resolva a desigualdade de valor absoluto algebricamente.
- Encontre pontos de limite resolvendo\(|x−A|=B\).
- Intervalos de teste criados pelos pontos limite para determinar onde\(|x−A|{\leq}B\).
- Escreva o intervalo ou a união de intervalos que satisfazem a desigualdade em notação de intervalo, desigualdade ou construtor de conjuntos.
Exemplo\(\PageIndex{6}\): Solving an Absolute Value Inequality
Resolver\(|x −5|{\leq}4\).
Solução
Com ambas as abordagens, precisaremos saber primeiro onde a igualdade correspondente é verdadeira. Nesse caso, primeiro descobriremos onde\(|x−5|=4\). Fazemos isso porque o valor absoluto é uma função sem quebras, então a única maneira de os valores da função mudarem de menores que 4 para maiores que 4 é passando por onde os valores são iguais a 4. Resolver\(|x−5|=4\).
\[\begin{align*} x−5&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−5&=−4 & x&=1\end{align*}\]
Depois de determinar que o valor absoluto é igual a 4 em\(x=1\) e\(x=9\), sabemos que o gráfico só pode mudar de menor que 4 para maior que 4 nesses valores. Isso divide a linha numérica em três intervalos:
\[x<1,\; 1<x<9, \text{ and } x>9. \nonumber\]
Para determinar quando a função é menor que 4, podemos escolher um valor em cada intervalo e ver se a saída é menor ou maior que 4, conforme mostrado na Tabela\(\PageIndex{1}\).
| Teste de intervalo\(x\) | \(f(x)\) | \(<4\)ou\(>4\) | |
|---|---|---|---|
| \ (x\)” style="alinhamento vertical: meio; ">\(x<1\) | \ (f (x)\)” style="alinhamento vertical:médio; ">0 | \ (<4\) ou\(>4\) "style="vertical-align:middle;" >\(|0-5|=5\) | Maior que |
| \ (x\)” style="alinhamento vertical: meio; ">\(1<x<9\) | \ (f (x)\)” style="alinhamento vertical:médio; ">6 | \ (<4\) ou\(>4\) "style="vertical-align:middle;" >\(|6-5|=1\) | Menos que |
| \ (x\)” style="alinhamento vertical: meio; ">\(x>9\) | \ (f (x)\)” style="alinhamento vertical:médio; ">11 | \ (<4\) ou\(>4\) "style="vertical-align:middle;" >\(|11-5|=6\) | Maior que |
Como\(1{\leq}x{\leq}9\) é o único intervalo em que a saída no valor do teste é menor que 4, podemos concluir que a solução para\(|x−5|{\leq}4\) é\(1{\leq}x{\leq}9\), ou\([1,9]\).
Para usar um gráfico, podemos esboçar a função\(f(x)=|x−5|\). Para nos ajudar a ver onde as saídas estão 4, a linha também\(g(x)=4\) pode ser esboçada como na Figura\(\PageIndex{11}\).
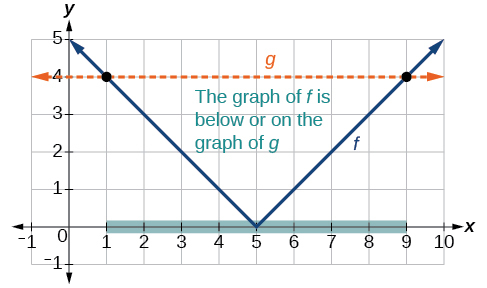
Podemos ver o seguinte:
- Os valores de saída do valor absoluto são iguais a 4 em\(x=1\)\(x=9\) e.
- O gráfico de\(f\) está abaixo do gráfico de\(g\) on\(1<x<9\). Isso significa que os valores de saída de\(f(x)\) são menores que os valores de saída de\(g(x)\).
- O valor absoluto é menor ou igual a 4 entre esses dois pontos, quando\(1{\leq}x\leq9\). Na notação de intervalo, esse seria o intervalo\([1,9]\).
Análise
Para desigualdades de valor absoluto,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; x−A<−C \text{ or } x−A>C. \nonumber\]
O\(>\) símbolo\(<\) ou pode ser substituído por\(\leq\) ou\(\geq\).
Então, para este exemplo, poderíamos usar essa abordagem alternativa.
\[\begin{align*} |x−5|&{\leq}4 \\ −4&{\leq}x−5{\leq}4 &\text{Rewrite by removing the absolute value bars.} \\ −4+5&{\leq}x−5+5{\leq}4+5 &\text{Isolate the x.} \\ 1&{\leq}x\leq9 \end{align*}\]
Exercício\(\PageIndex{5}\)
Resolver\(|x+2| \leq 6\).
- Responda
-
\(-8 \leq x \leq 4\)
Como fazer...
Dada uma função de valor absoluto, resolva o conjunto de entradas em que a saída é positiva (ou negativa).
- Defina a função igual a zero e resolva os pontos limite do conjunto de soluções.
- Use pontos de teste ou um gráfico para determinar onde a saída da função é positiva ou negativa.
Exemplo\(\PageIndex{7}\): Using a Graphical Approach to Solve Absolute Value Inequalities
Dada a função\(f(x)=−\frac{1}{2}|4x−5|+3\), determine os\(x\) valores -para os quais os valores da função são negativos.
Solução
Estamos tentando determinar onde\(f(x)<0\), que é quando\(−\frac{1}{2}|4x−5|+3<0\). Começamos isolando o valor absoluto.
\[ \begin{align*} -\frac{1}{2}|4x−5|&<−3 \;\;\; \text{Multiply both sides by –2, and reverse the inequality.} \\ |4x−5|&>6\end{align*}\]
Em seguida, resolvemos a igualdade\(|4x−5|=6\).
\[\begin{align*} 4x-5&=6 & 4x-5&=-6 \\ 4x-6&=6 \end{align*}\]
ou
\[\begin{align*} 4x&=-1 \\ x&=\frac{11}{4} & x&=-\frac{1}{4} \end{align*}\]
Agora, podemos examinar o gráfico de\(f\) para observar onde a saída é negativa. Observaremos onde os galhos estão abaixo\(x\) do eixo. Observe que nem é importante exatamente a aparência do gráfico, desde que saibamos que ele cruza o eixo horizontal\(x=−\frac{1}{4}\)\(x=\frac{11}{4}\) e que o gráfico foi refletido verticalmente. Veja a Figura\(\PageIndex{12}\).
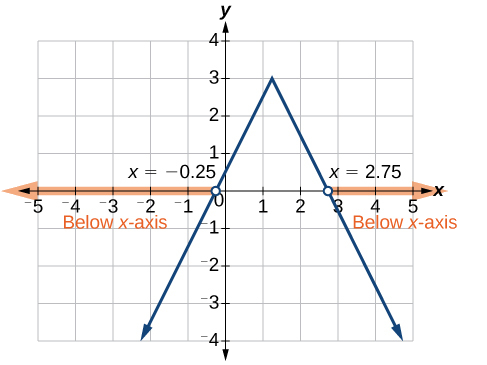
Observamos que o gráfico da função está abaixo do\(x\) eixo -à esquerda\(x=−\frac{1}{4}\) e à direita de\(x=\frac{11}{4}\). Isso significa que os valores da função são negativos à esquerda da primeira interceptação horizontal em\(x=−\frac{1}{4}\) e negativos à direita da segunda interceptação em\(x=\frac{11}{4} \). Isso nos dá a solução para a desigualdade.
\[x<−\frac{1}{4} \text{ or } x>1\frac{1}{4} \nonumber\]
Na notação de intervalo, isso seria\(( −\infty,−0.25 )\cup( 2.75,\infty)\).
Exercício\(\PageIndex{6}\)
Resolver\(−2|k−4|\leq−6\).
- Responda
-
\(k\leq1\)ou\(k\geq7\); em notação de intervalo, isso seria\(\left(−\infty,1\right]\cup\left[7,\infty\right)\)
Conceitos-chave
- A função de valor absoluto é comumente usada para medir distâncias entre pontos.
- Problemas aplicados, como faixas de valores possíveis, também podem ser resolvidos usando a função de valor absoluto.
- O gráfico da função de valor absoluto se assemelha a uma letra V. Ele tem um ponto angular no qual o gráfico muda de direção.
- Em uma equação de valor absoluto, uma variável desconhecida é a entrada de uma função de valor absoluto.
- Se o valor absoluto de uma expressão for definido como igual a um número positivo, espere duas soluções para a variável desconhecida.
- Uma equação de valor absoluto pode ter uma solução, duas soluções ou nenhuma solução.
- Uma desigualdade de valor absoluto é semelhante a uma equação de valor absoluto<B, | A |≤B, | A |>, mas assume a forma | A |B ou | A |≥B.Ela pode ser resolvida determinando os limites do conjunto de soluções e depois testando quais segmentos estão no conjunto.
- As desigualdades de valor absoluto também podem ser resolvidas graficamente.
Glossário
equação de valor absoluto
uma equação da forma\(|A|=B\), com\(B\geq0\); ela terá soluções quando\(A=B\) ou\(A=−B\)
desigualdade de valor absoluto:
uma relação na forma\(|A|<B\),\(|A|{\leq}B\),\(|A|>B\), ou\(|A|{\geq}B\)


