3.3: Taxas de mudança e comportamento dos gráficos

Last updated
Save as PDF

Page ID: 186962

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Encontre a taxa média de variação de uma função.
Use um gráfico para determinar onde uma função está aumentando, diminuindo ou constante.
Use um gráfico para localizar máximos e mínimos locais.
Use um gráfico para localizar o máximo absoluto e o mínimo absoluto.

Os custos da gasolina sofreram grandes flutuações nas últimas décadas. A tabela$\PageIndex{1}$ lista o custo médio, em dólares, de um galão de gasolina para os anos de 2005 a 2012. O custo da gasolina pode ser considerado em função do ano.

Tabela$\PageIndex{1}$
$y$	2005	2006	2007	2008	2009	2010	2011	2012
$C(y)$	2.31	2,62	2,84	3,30	2,41	2,84	3,58	3,68

Se estivéssemos interessados apenas em como os preços da gasolina mudaram entre 2005 e 2012, poderíamos calcular que o custo por galão aumentou de $2,31 para $3,68, um aumento de $1,37. Embora isso seja interessante, pode ser mais útil observar o quanto o preço mudou por ano. Nesta seção, investigaremos mudanças como essas.

Encontrando a taxa média de variação de uma função

A mudança de preço por ano é uma taxa de variação porque descreve como uma quantidade de saída muda em relação à mudança na quantidade de entrada. Podemos ver que o preço da gasolina na Tabela$\PageIndex{1}$ não mudou na mesma quantidade a cada ano, então a taxa de variação não foi constante. Se usarmos apenas os dados iniciais e finais, encontraríamos a taxa média de variação durante o período de tempo especificado. Para encontrar a taxa média de variação, dividimos a mudança no valor de saída pela mudança no valor de entrada.

\[\begin{align*} \text{Average rate of change}&=\dfrac{\text{Change in output}}{\text{Change in input}} \\[4pt] &=\dfrac{\Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\end{align*} \label{1.3.1}\]

A letra grega$\Delta$ (delta) significa a mudança em uma quantidade; lemos a proporção como “delta-$y$ sobre delta-$x$” ou “a mudança em$y$ dividido pela mudança em”$x$. Ocasionalmente$\Delta y$, escrevemos$\Delta f$ em vez de, o que ainda representa a mudança no valor de saída da função resultante de uma alteração em seu valor de entrada. Isso não significa que estamos transformando a função em outra função.

Em nosso exemplo, o preço da gasolina aumentou em $1,37 de 2005 a 2012. Em 7 anos, a taxa média de mudança foi

\[\dfrac{\Delta y}{\Delta x}=\dfrac{$1.37}{7 \text{years}}\approx \text{0.196 dollars per year.} \label{1.3.2}\]

Em média, o preço do gás aumentou cerca de 19,6 centavos a cada ano. Outros exemplos de taxas de variação incluem:

Uma população de ratos aumentando em 40 ratos por semana
Um carro viajando 68 milhas por hora (a distância percorrida muda em 68 milhas a cada hora com o passar do tempo)
Um carro dirigindo 27 milhas por galão (a distância percorrida muda em 27 milhas para cada galão)
A corrente através de um circuito elétrico aumenta em 0,125 amperes para cada volt de aumento de tensão
A quantidade de dinheiro em uma conta universitária diminui em $4.000 por trimestre

Definição: Taxa de variação

Uma taxa de variação descreve como uma quantidade de saída muda em relação à mudança na quantidade de entrada. As unidades em uma taxa de variação são “unidades de saída por unidade de entrada”.

A taxa média de variação entre dois valores de entrada é a mudança total dos valores da função (valores de saída) dividida pela mudança nos valores de entrada.

\[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\]

Como fazer...

Dado o valor de uma função em pontos diferentes, calcule a taxa média de variação de uma função para o intervalo entre dois valores$x_1$$x_2$ e.

Calcule a diferença$y_2−y_1=\Delta y$.
Calcule a diferença$x_2−x_1=\Delta x$.
Encontre a proporção$\dfrac{\Delta y}{\Delta x}$.

Exemplo$\PageIndex{1}$: Computing an Average Rate of Change

Usando os dados da Tabela$\PageIndex{1}$, encontre a taxa média de variação do preço da gasolina entre 2007 e 2009.

Solução

Em 2007, o preço da gasolina foi de $2,84. Em 2009, o custo foi de $2,41. A taxa média de mudança é

\[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2.41−$2.84}{2009−2007} \\[4pt] &=\dfrac{−$0.43}{2 \text{ years}} \\[4pt] &=−$0.22 \text{ per year} \end{align*}\]

Análise

Observe que uma diminuição é expressa por uma mudança negativa ou “aumento negativo”. Uma taxa de variação é negativa quando a saída diminui à medida que a entrada aumenta ou quando a saída aumenta à medida que a entrada diminui.

Exercício$\PageIndex{1}$

Usando os dados na Tabela$\PageIndex{1}$, encontre a taxa média de variação entre 2005 e 2010.

Solução: $\dfrac{$2.84−$2.315}{5 \text{ years}} =\dfrac{$0.535}{5 \text{ years}} =$0.106 \text{per year.}$

Exemplo$\PageIndex{2}$: Computing Average Rate of Change from a Graph

Dada a função$g(t)$ mostrada na Figura$\PageIndex{1}$, encontre a taxa média de variação no intervalo$[−1,2]$.

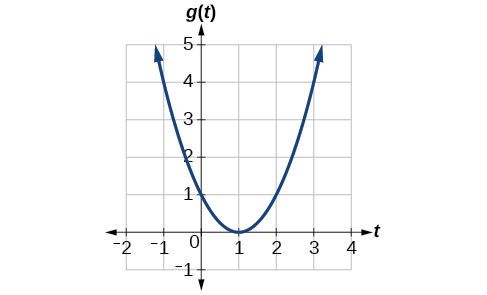
Figura$\PageIndex{1}$: Gráfico de uma parábola.

Solução

Em$t=−1$,$\PageIndex{2}$ mostra a figura$g(−1)=4$. Em$t=2$, o gráfico mostra$g(2)=1$.

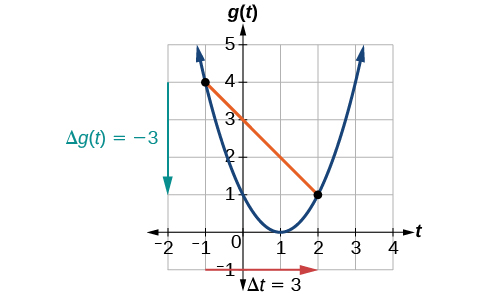
Figura$\PageIndex{2}$: Gráfico de uma parábola com uma linha dos pontos (-1, 4) e (2, 1) para mostrar as mudanças de g (t) e t.

A mudança horizontal$\Delta t=3$ é mostrada pela seta vermelha e a mudança vertical$\Delta g(t)=−3$ é mostrada pela seta turquesa. A saída muda em —3 enquanto a entrada muda em 3, fornecendo uma taxa média de variação de

\[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\]

Análise

Observe que o pedido que escolhemos é muito importante. Se, por exemplo, usarmos$\dfrac{y_2−y_1}{x_1−x_2}$, não obteremos a resposta correta. Decida qual ponto será 1 e qual ponto será 2 e mantenha as coordenadas fixas como$(x_1,y_1)$$(x_2,y_2)$ e.

Exemplo$\PageIndex{3}$: Computing Average Rate of Change from a Table

Depois de pegar uma amiga que mora a 10 milhas de distância, Anna registra sua distância de casa ao longo do tempo. Os valores são mostrados na Tabela$\PageIndex{2}$. Encontre sua velocidade média nas primeiras 6 horas.

Tabela$\PageIndex{2}$
$t$(horas)	0	1	2	3	4	5	6	7
$D(t)$(milhas)	10	55	90	153	214	240	292	300

Solução

Aqui, a velocidade média é a taxa média de mudança. Ela viajou 292 milhas em 6 horas, para uma velocidade média de

\[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\]

A velocidade média é de cerca de 47 milhas por hora.

Análise

Como a velocidade não é constante, a velocidade média depende do intervalo escolhido. Para o intervalo$[2,3]$, a velocidade média é de 63 milhas por hora.

Exemplo$\PageIndex{4}$: Computing Average Rate of Change for a Function Expressed as a Formula

Calcule a taxa média de variação de$f(x)=x^2−\frac{1}{x}$ no intervalo$[2, 4]$.

Solução

Podemos começar computando os valores da função em cada ponto final do intervalo.

\[\begin{align*}f(2)&=2^2−\frac{1}{2} f(4)&=4^2−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\frac{63}{4}\end{align*}\]

Agora, calculamos a taxa média de variação.

\[\begin{align*}\text{Average rate of change} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac{63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\]

Exercício$\PageIndex{2}$

Encontre a taxa média de variação de$f(x)=x−2\sqrt{x}$ no intervalo$[1, 9]$.

Solução: $\frac{1}{2}$

Exemplo$\PageIndex{5}$: Finding the Average Rate of Change of a Force

A força eletrostática$F$, medida em newtons, entre duas partículas carregadas pode ser relacionada à distância entre as partículas$d$, em centímetros, pela fórmula$F(d)=\frac{2}{d^2}$. Encontre a taxa média de mudança de força se a distância entre as partículas for aumentada de 2 cm para 6 cm.

Solução

Estamos calculando a taxa média de variação de$F(d)=\dfrac{2}{d^2}$ no intervalo$[2,6]$.

\[\begin{align*}\text{Average rate of change }&=\dfrac{F(6)−F(2)}{6−2} \\[4pt] &=\dfrac{\frac{2}{6^2}-\frac{2}{2^2}}{6-2} & \text{Simplify} \\[4pt] &=\dfrac{\frac{2}{36}-\frac{2}{4}}{4} \\[4pt] &=\dfrac{-\frac{16}{36}}{4} & \text{Combine numerator terms.} \\[4pt] &=−\dfrac{1}{9} & \text{Simplify}\end{align*}\]

A taxa média de mudança é de$−\frac{1}{9}$ newton por centímetro.

Exemplo$\PageIndex{6}$: Finding an Average Rate of Change as an Expression

Encontre a taxa média de variação de$g(t)=t^2+3t+1$ no intervalo$[0, a]$. A resposta será uma expressão envolvente$a$.

Solução

Usamos a fórmula da taxa média de mudança.

$\begin{align*}\text{Average rate of change} &=\dfrac{g(a)−g(0)}{a−0} & \text{Evaluate.} \\[4pt] &=\dfrac{(a^2+3a+1)−(0^2+3(0)+1)}{a−0} & \text{Simplify.} \\[4pt] &=\dfrac{a^2+3a+1−1}{a} & \text{Simplify and factor.}\\[4pt] &= \dfrac{a(a+3)}{a} & \text{Divide by the common factor a.}\\[4pt] &= a+3 \end{align*}$

Esse resultado nos mostra a taxa média de variação em termos de um intervalo$t=0$ e qualquer outro ponto$t=a$. Por exemplo, no intervalo$[0,5]$, a taxa média de mudança seria$5+3=8$.

Exercício$\PageIndex{3}$

Encontre a taxa média de variação de$f(x)=x^2+2x−8$ no intervalo$[5, a]$.

Solução: $a+7$

Usando um gráfico para determinar onde uma função está aumentando, diminuindo ou constante

Como parte da exploração de como as funções mudam, podemos identificar intervalos nos quais a função está mudando de maneiras específicas. Dizemos que uma função está aumentando em um intervalo se os valores da função aumentarem à medida que os valores de entrada aumentam dentro desse intervalo. Da mesma forma, uma função está diminuindo em um intervalo se os valores da função diminuírem à medida que os valores de entrada aumentam nesse intervalo. A taxa média de variação de uma função crescente é positiva e a taxa média de variação de uma função decrescente é negativa. A figura$\PageIndex{3}$ mostra exemplos de intervalos crescentes e decrescentes em uma função.

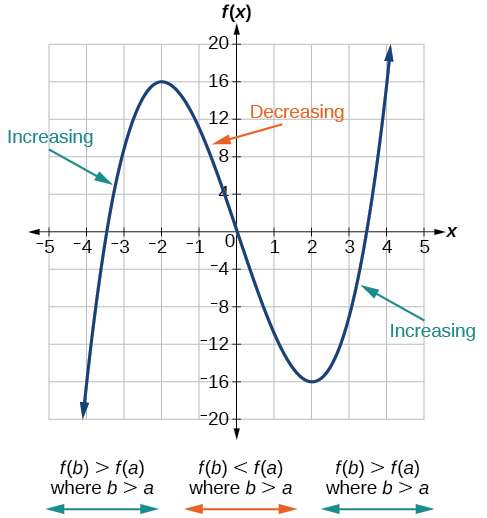
Gráfico de um polinômio que mostra os intervalos crescentes e decrescentes e o máximo e mínimo locais. — Figura$\PageIndex{3}$: A função$f(x)=x^3−12x$ está aumentando$(−\infty, −2)\cup (2,\infty)$ e diminuindo$(−2, 2)$.

Embora algumas funções estejam aumentando (ou diminuindo) em todo o seu domínio, muitas outras não estão. Um valor da entrada em que uma função muda de crescente para decrescente (à medida que vamos da esquerda para a direita, ou seja, à medida que a variável de entrada aumenta) é chamado de máximo local. Se uma função tiver mais de um, dizemos que ela tem máximos locais. Da mesma forma, um valor da entrada em que uma função muda de decrescente para crescente à medida que a variável de entrada aumenta é chamado de mínimo local. A forma plural é “mínimos locais”. Juntos, máximos e mínimos locais são chamados de extremos locais, ou valores extremos locais, da função. (A forma singular é “extremum”.) Muitas vezes, o termo local é substituído pelo termo relativo. Neste texto, usaremos o termo local.

Claramente, uma função não está aumentando nem diminuindo em um intervalo em que é constante. Uma função também não está aumentando nem diminuindo em extremos. Observe que temos que falar de extrema local, porque qualquer extremidade local, conforme definida aqui, não é necessariamente a máxima mais alta ou a mínima mais baixa em todo o domínio da função.

Para a função cujo gráfico é mostrado na Figura$\PageIndex{4}$, o máximo local é 16 e ocorre em$x=−2$. O mínimo local é −16 e ocorre em$x=2$.

Gráfico de um polinômio que mostra os intervalos crescentes e decrescentes e o máximo local.] Definição de um máximo local — Figura$\PageIndex{4}$: Gráfico de um polinômio que mostra os intervalos crescentes e decrescentes e o máximo local.máximo

Para localizar os máximos e mínimos locais a partir de um gráfico, precisamos observar o gráfico para determinar onde o gráfico atinge seus pontos mais altos e mais baixos, respectivamente, dentro de um intervalo aberto. Como o cume de uma montanha-russa, o gráfico de uma função é maior em um máximo local do que em pontos próximos em ambos os lados. O gráfico também será menor no mínimo local do que nos pontos vizinhos. A figura$\PageIndex{5}$ ilustra essas ideias para um máximo local.

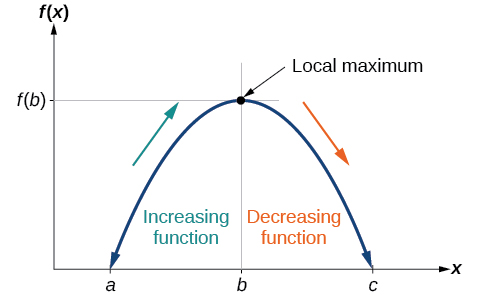
Gráfico de um polinômio que mostra os intervalos crescentes e decrescentes e o máximo local. — Figura$\PageIndex{5}$: Definição de um máximo local

Essas observações nos levam a uma definição formal de extremos locais.

Mínimos locais e máximos locais

Uma função$f$ é uma função crescente em um intervalo aberto se$f(b)>f(a)$ para cada$a$$b$ intervalo onde$b>a$.
Uma função$f$ é uma função decrescente em um intervalo aberto se$f(b)<f(a)$ para cada$a$$b$ intervalo onde$b>a$.

Uma função$f$ tem um máximo local em um ponto$b$ em um intervalo aberto$(a,c)$ se$f(b)$ for maior ou igual a$f(x)$ para cada ponto$x$ ($x$não é igual$b$) no intervalo. Da mesma forma,$f$ tem um mínimo local$b$ em$(a,c)$ se$f(b)$ for menor ou igual a$f(x)$ para cada$x$ ($x$não é igual$b$) no intervalo.

Exemplo$\PageIndex{7}$ Finding Increasing and Decreasing Intervals on a Graph

Dada a função$p(t)$ na Figura$\PageIndex{6}$, identifique os intervalos nos quais a função parece estar aumentando.

[Gráfico de um polinômio.] — Figura$\PageIndex{6}$: Gráfico de um polinômio.

Solução

Vemos que a função não é constante em nenhum intervalo. A função está aumentando onde ela se inclina para cima à medida que nos movemos para a direita e diminuindo onde ela se inclina para baixo à medida que nos movemos para a direita. A função parece estar aumentando de$t=1$ para$t=3$ e de$t=4$ em diante.

Na notação de intervalo, diríamos que a função parece estar aumentando no intervalo$(1,3)$ e no intervalo$(4,\infty)$.

Análise

Observe neste exemplo que usamos intervalos abertos (intervalos que não incluem os pontos finais), porque a função não está aumentando nem diminuindo em$t=1$$t=3$,$t=4$ e. Esses pontos são os extremos locais (dois mínimos e um máximo).

Exemplo$\PageIndex{8}$: Finding Local Extrema from a Graph

Faça um gráfico da função$f(x)=\frac{2}{x}+\frac{x}{3}$. Em seguida, use o gráfico para estimar a extremidade local da função e determinar os intervalos nos quais a função está aumentando.

Solução

Usando a tecnologia, descobrimos que o gráfico da função se parece com o da Figura$\PageIndex{7}$. Parece que há um ponto baixo, ou mínimo local, entre$x=2$ e$x=3$, e um ponto alto de imagem espelhada, ou máximo local, em algum lugar entre$x=−3$ e$x=−2$

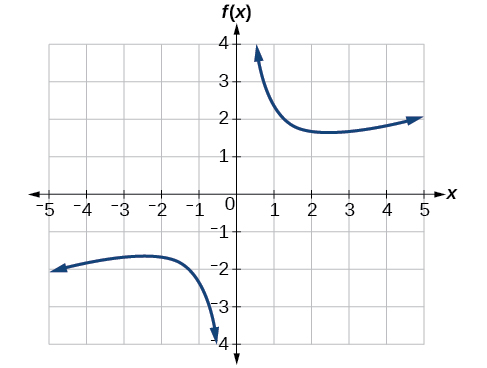Figura$\PageIndex{7}$: Gráfico de uma função recíproca.

Análise

A maioria das calculadoras gráficas e utilitários gráficos podem estimar a localização de máximos e mínimos. $\PageIndex{8}$A figura fornece imagens de tela de duas tecnologias diferentes, mostrando a estimativa para o máximo e mínimo locais.

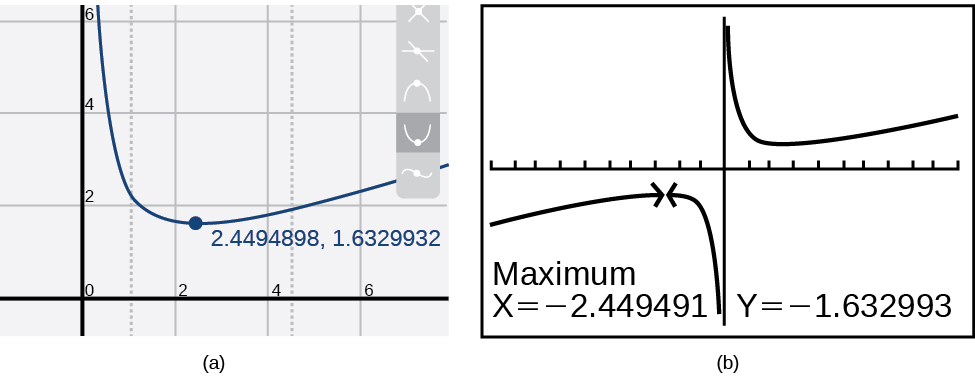
Figura$\PageIndex{8}$: Gráfico da função recíproca em uma calculadora gráfica.

Com base nessas estimativas, a função está aumentando no intervalo$(−\infty,−2.449)$$(2.449,\infty)$ e. Observe que, embora esperemos que os extremos sejam simétricos, as duas tecnologias diferentes concordam com apenas até quatro decimais devido aos diferentes algoritmos de aproximação usados por cada uma. (A localização exata da extremidade é em$\pm\sqrt{6}$, mas determinar isso requer cálculo.)

Exercício$\PageIndex{8}$

Faça um gráfico da função$f(x)=x^3−6x^2−15x+20$ para estimar a extremidade local da função. Use-os para determinar os intervalos nos quais a função está aumentando e diminuindo.

Solução

O máximo local parece ocorrer em$(−1,28)$, e o mínimo local ocorre em$(5,−80)$. A função está aumentando$(−\infty,−1)\cup(5,\infty)$ e diminuindo$(−1,5)$.

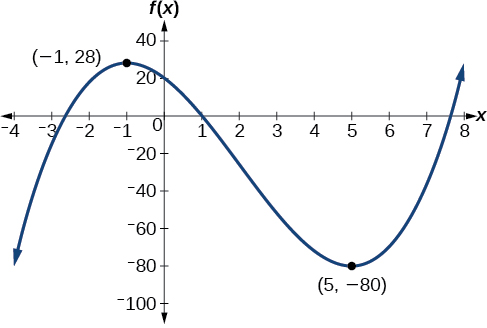
$Gráfico de um polinômio com um máximo local em (-1, 28) e mínimo local em (5, -80).$

Gráfico de um polinômio com um máximo local em (-1, 28) e mínimo local em (5, -80).

Exemplo$\PageIndex{9}$: Finding Local Maxima and Minima from a Graph

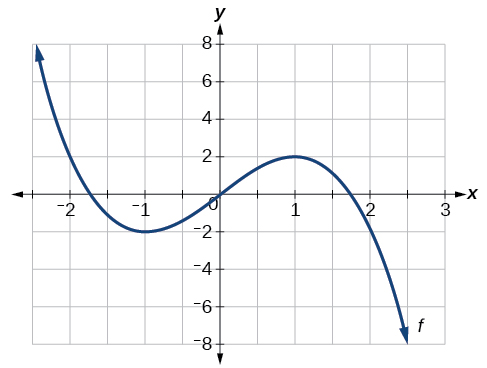
Para a função f cujo gráfico é mostrado na Figura$\PageIndex{9}$, encontre todos os máximos e mínimos locais.

Solução

Observe o gráfico de$f$. O gráfico atinge um máximo local em$x=1$ porque é o ponto mais alto em um intervalo aberto em torno de$x=1$ .O máximo local é a coordenada y em$x=1$, que é 2.

O gráfico atinge um mínimo local em$x=−1$ porque é o ponto mais baixo em um intervalo aberto ao redor$x=−1$. O mínimo local é a coordenada y em$x=−1$, que é −2.

Analisando as funções do kit de ferramentas para aumentar ou diminuir os intervalos

Agora retornaremos às funções do nosso kit de ferramentas e discutiremos seu comportamento gráfico em Figura$\PageIndex{10}$$\PageIndex{11}$, Figura e Figura$\PageIndex{12}$.

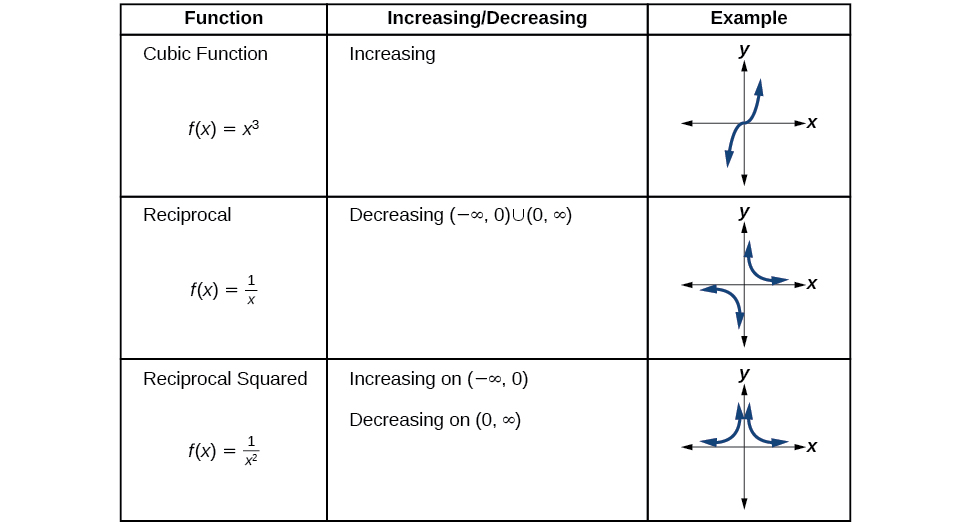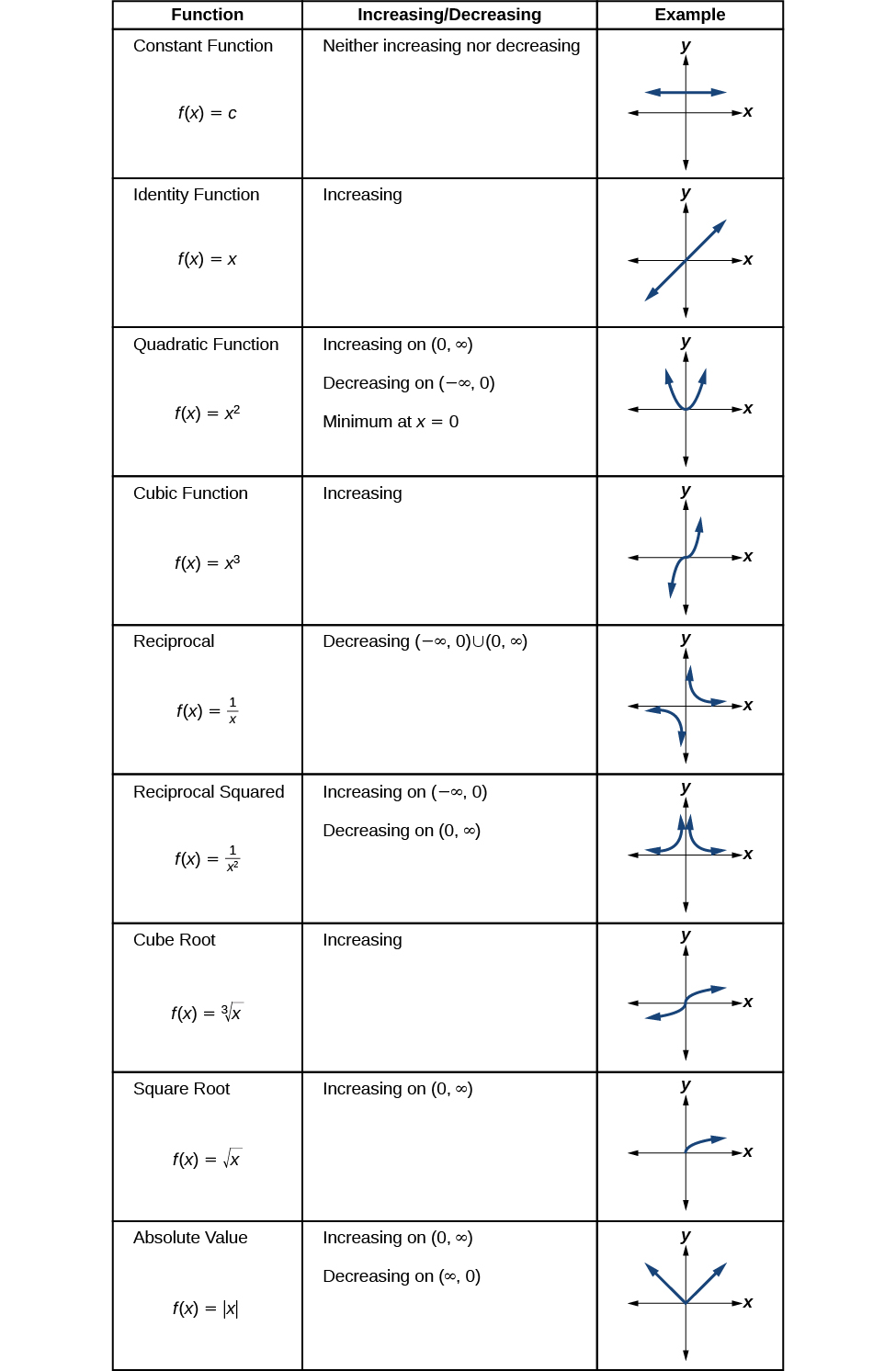
$Tabela mostrando os intervalos crescentes e decrescentes das funções do kit de ferramentas.$
Figura$\PageIndex{12}$

Use um gráfico para localizar o máximo absoluto e o mínimo absoluto

Há uma diferença entre localizar os pontos mais altos e mais baixos em um gráfico em uma região em torno de um intervalo aberto (localmente) e localizar os pontos mais altos e mais baixos no gráfico para todo o domínio. As coordenadas y (saída) nos pontos mais altos e mais baixos são chamadas de máximo absoluto e mínimo absoluto, respectivamente. Para localizar máximos e mínimos absolutos a partir de um gráfico, precisamos observar o gráfico para determinar onde o gráfico atinge seus pontos mais altos e mais baixos no domínio da função (Figura$\PageIndex{13}$).

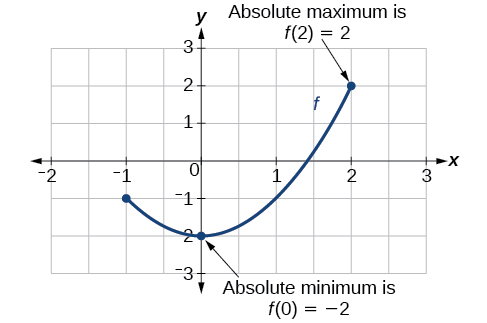
Figura$\PageIndex{13}$: Gráfico de um segmento de uma parábola com um mínimo absoluto em (0, -2) e máximo absoluto em (2, 2).

Nem toda função tem um valor máximo ou mínimo absoluto. A função do kit de ferramentas$f(x)=x^3$ é uma dessas funções.

Máximos e mínimos absolutos

O máximo absoluto de$f$ at$x=c$ é$f(c)$ onde$f(c)≥f(x)$ para todos$x$ no domínio de$f$.
O mínimo absoluto de$f$ at$x=d$ é$f(d)$ onde$f(d)≤f(x)$ para todos$x$ no domínio de$f$.

Exemplo$\PageIndex{10}$: Finding Absolute Maxima and Minima from a Graph

Para a função f mostrada na Figura$\PageIndex{14}$, encontre todos os máximos e mínimos absolutos.

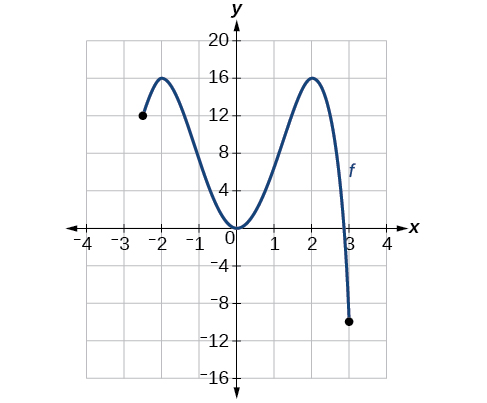
Solução

Observe o gráfico de$f$. O gráfico atinge um máximo absoluto em dois locais$x=−2$ e$x=2$, porque nesses locais, o gráfico atinge seu ponto mais alto no domínio da função. O máximo absoluto é a coordenada y em$x=−2$ e$x=2$, que é 16.

$O gráfico atinge um mínimo absoluto em x=3, porque é o ponto mais baixo no domínio do gráfico da função. O mínimo absoluto é a coordenada y em x=3, que é -10.$

Equações-chave

Taxa média de variação:$\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}$

Conceitos-chave

Uma taxa de variação relaciona uma mudança em uma quantidade de saída a uma mudança em uma quantidade de entrada. A taxa média de mudança é determinada usando somente os dados iniciais e finais. Veja o exemplo.
Os pontos de identificação que marcam o intervalo em um gráfico podem ser usados para encontrar a taxa média de variação. Veja o exemplo.
A comparação de pares de valores de entrada e saída em uma tabela também pode ser usada para encontrar a taxa média de variação. Veja o exemplo.
Uma taxa média de variação também pode ser calculada determinando os valores da função nos pontos finais de um intervalo descrito por uma fórmula. Veja o exemplo e o exemplo.
Às vezes, a taxa média de mudança pode ser determinada como uma expressão. Veja o exemplo.
Uma função está aumentando quando sua taxa de mudança é positiva e diminuindo onde sua taxa de mudança é negativa. Veja o exemplo.
Um máximo local é quando uma função muda de crescente para decrescente e tem um valor de saída maior (mais positivo ou menos negativo) do que os valores de saída em valores de entrada vizinhos.
Um mínimo local é quando a função muda de decrescente para crescente (à medida que a entrada aumenta) e tem um valor de saída menor (mais negativo ou menos positivo) do que os valores de saída em valores de entrada vizinhos.
Mínimos e máximos também são chamados de extremos.
Podemos encontrar a extremidade local a partir de um gráfico. Veja o exemplo e o exemplo.
Os pontos mais altos e mais baixos em um gráfico indicam os máximos e mínimos. Veja o exemplo.

\(y\)	2005	2006	2007	2008	2009	2010	2011	2012
\(C(y)\)	2.31	2,62	2,84	3,30	2,41	2,84	3,58	3,68