1.5: Fatorando polinômios
- Page ID
- 186807
Nesta seção, os alunos irão:
- Fator o maior fator comum de um polinômio.
- Fator um trinômio.
- Fator por agrupamento.
- Considere um trinômio quadrado perfeito.
- Fator a diferença de quadrados.
- Considere a soma e a diferença dos cubos.
- Expressões fatoriais usando expoentes fracionários ou negativos.
Imagine que estamos tentando encontrar a área de um gramado para que possamos determinar a quantidade de sementes de capim a serem compradas. O gramado é a parte verde na Figura\(\PageIndex{1}\).
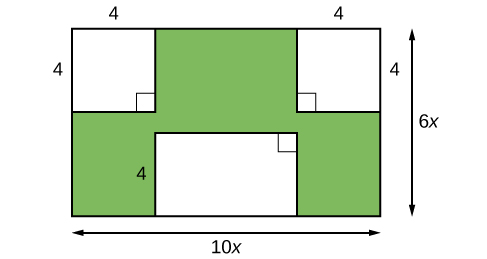
A área de toda a região pode ser encontrada usando a fórmula para a área de um retângulo.
\[\begin{align*} A &= lw\\ &= 10x\times6x\\ &= 60x^2\; units^2 \end{align*}\]
As áreas das porções que não necessitam de sementes de capim precisam ser subtraídas da área de toda a região. Cada uma das duas regiões quadradas tem uma área de\(A =s^2=4^2= 16\; units^2\). A outra região retangular tem um lado de comprimento\(10x−8\) e um lado de comprimento\(4\), dando uma área de
\[A =lw=4(10x−8)=40x−32\; \text{units}^2. \nonumber\]
Portanto, a região que deve ser subtraída tem uma área de
\[2(16)+40x−32= 40x\; \text{units}^2. \nonumber\]
A área da região que requer sementes de capim é encontrada subtraindo\(60x^2−40x\; \text{units}^2\). Essa área também pode ser expressa de forma fatorada como\(20x (3x−2)\; \text{units}^2\). Podemos confirmar que essa é uma expressão equivalente multiplicando.
Muitas expressões polinomiais podem ser escritas em formas mais simples por meio de fatoração. Nesta seção, veremos uma variedade de métodos que podem ser usados para fatorar expressões polinomiais.
Fatorando o maior fator comum de um polinômio
Quando estudamos frações, aprendemos que o maior fator comum (GCF) de dois números é o maior número que se divide igualmente em ambos os números. Por exemplo,\(4\) é o GCF de\(16\) e\(20\) porque é o maior número que se divide uniformemente em ambos\(16\) e\(20\) O GCF dos polinômios funciona da mesma maneira:\(4x\) é o GCF de\(16x\) e\(20x^2\) porque é o maior polinômio que se divide uniformemente em ambos\(16x\)\(20x^2\) e.
Ao fatorar uma expressão polinomial, nosso primeiro passo deve ser verificar se há um GCF. Procure o GCF dos coeficientes e, em seguida, procure o GCF das variáveis.
O maior fator comum (GCF) dos polinômios é o maior polinômio que se divide uniformemente entre os polinômios.
- Identifique o GCF dos coeficientes.
- Identifique o GCF das variáveis.
- Combine para encontrar o GCF da expressão.
- Determine por que o GCF precisa ser multiplicado para obter cada termo na expressão.
- Escreva a expressão fatorada como o produto do GCF e a soma dos termos pelos quais precisamos multiplicar.
Fator\(6x^3y^3 +45x^2y^2+21xy\).
Solução
Primeiro, encontre o GCF da expressão. O GCF de\(6\),\(45\), e\(21\) é\(3\). O GCF de\(x^3\),\(x^2\), e\(x\) é\(x\). (Observe que o GCF de um conjunto de expressões no formulário sempre\(x^n\) será o expoente do menor grau.) E o GCF de\(y^3\)\(y^2\), e\(y\) é\(y\). Combine-os para encontrar o GCF do polinômio,\(3xy\).
Em seguida, determine por que o GCF precisa ser multiplicado para obter cada termo do polinômio. Nós descobrimos que
- \(3xy(2x^2y^2)=6x^3y^3\),
- \(3xy(15xy)=45x^2y^2\), e
- \(3xy(7)=21xy\).
Finalmente, escreva a expressão fatorada como o produto do GCF e a soma dos termos pelos quais precisávamos multiplicar.
\[(3xy)(2x^2y^2+15xy+7) \nonumber\]
Análise
Após a fatoração, podemos verificar nosso trabalho multiplicando. Use a propriedade distributiva para confirmar que
\[(3xy)(2x^2y^2+15xy+7)=6x^3y^3+45x^2y^2+21xy \nonumber\]
Considere\(x(b^2−a)+6(b^2−a)\) retirando o GCF.
- Responda
-
\((b^2−a)(x+6)\)
Fatorando um trinômio com o coeficiente principal 1
Embora devamos sempre começar procurando por um GCF, retirar o GCF não é a única maneira pela qual expressões polinomiais podem ser fatoradas. O polinômio\(x^2+5x+6\) tem um GCF de\(1\), mas pode ser escrito como o produto dos fatores\((x+2)\)\((x+3)\) e.
Os trinômios da forma\(x^2+bx+c\) podem ser fatorados encontrando dois números com um produto de\(c\) e uma soma de\(b\). O trinômio\(x^2+10x+16\), por exemplo, pode ser fatorado usando os números\(2\) e\(8\) porque o produto desses números é\(16\) e sua soma é\(10\). O trinômio pode ser reescrito como produto de\((x+2)\)\((x+8)\) e.
Um trinômio da forma\(x^2+bx+c\) pode ser escrito de forma fatorada como\((x+p)(x+q)\) onde\(pq=c\)\(p+q=b\) e.
Não. Alguns polinômios não podem ser fatorados. Diz-se que esses polinômios são primos.
- Liste os fatores de\(c\).
- Encontre\(p\) e\(q\), um par de fatores de\(c\) com uma soma de\(b\).
- Escreva a expressão fatorada\((x+p)(x+q)\).
Fator\(x^2+2x−15\).
Solução
Temos um trinômio com coeficiente principal\(1\)\(b=2\),\(c=−15\) e. Precisamos encontrar dois números com um produto de\(−15\) e uma soma de\(2\). Na Tabela\(\PageIndex{1}\), listamos fatores até encontrarmos um par com a soma desejada.
| Fatores de −15 | Soma dos fatores |
|---|---|
| 1, −15 | −14 |
| −1,15 | 14 |
| 3, −5 | −2 |
| −3,5 |
Agora que identificamos\(p\) e\(q\) como\(−3\) e\(5\), escreva a forma fatorada como\((x−3)(x+5)\).
Análise
Podemos verificar nosso trabalho multiplicando. Use FOIL para confirmar isso\((x−3)(x+5)=x^2+2x−15\).
Não. A multiplicação é comutativa, então a ordem dos fatores não importa.
Fator\(x^2−7x+6\).
- Responda
-
\((x−6)(x−1)\)
Fatoração por agrupamento
Trinômios com coeficientes principais diferentes de\(1\) são um pouco mais complicados de fatorar. Para esses trinômios, podemos fatorar agrupando dividindo o termo x na soma de dois termos, fatorando cada parte da expressão separadamente e depois fatorando o GCF de toda a expressão. O trinômio\(2x^2+5x+3\) pode ser reescrito\((2x+3)(x+1)\) usando esse processo. Começamos reescrevendo a expressão original como\(2x^2+2x+3x+3\) e depois fatoramos cada parte da expressão a ser obtida\(2x(x+1)+3(x+1)\). Em seguida, retiramos o GCF de\((x+1)\) para encontrar a expressão fatorada.
Para fatorar um trinômio na forma\(ax^2+bx+c\) por agrupamento, encontramos dois números com um produto de\(ac\) e uma soma de\(b\). Usamos esses números para dividir o\(x\) termo na soma de dois termos e fatorar cada parte da expressão separadamente e, em seguida, fatorar o GCF de toda a expressão.
- Liste os fatores de\(ac\).
- Encontre\(p\) e\(q\), um par de fatores de\(ac\) com uma soma de\(b\).
- Reescreva a expressão original como\(ax^2+px+qx+c\).
- Retire o GCF de\(ax^2+px\).
- Retire o GCF de\(qx+c\).
- Considere o GCF da expressão.
Fator\(5x^2+7x−6\) por agrupamento.
Solução
Temos um trinômio com\(a=5\)\(b=7\),\(c=−6\) e. Primeiro, determine\(ac=−30\). Precisamos encontrar dois números com um produto de\(−30\) e uma soma de\(7\). Na tabela abaixo, listamos fatores até encontrarmos um par com a soma desejada.
| Fatores de −30 | Soma dos fatores |
|---|---|
| 1, −30 | −29 |
| −1,30 | 29 |
| 2, −15 | −13 |
| −2,15 | 13 |
| 3, −10 | −7 |
| −3,10 | 7 |
Então\(p=−3\)\(q=10\) e.
\(5x^2−3x+10x−6\)Reescreva a expressão original como\(ax^2+px+qx+c\).
\(x(5x−3)+2(5x−3)\)Considere o GCF de cada peça
\((5x−3)(x+2)\)Considere o GCF da expressão.
Análise
Podemos verificar nosso trabalho multiplicando. Use FOIL para confirmar isso\((5x−3)(x+2)=5x^2+7x−6\).
Fator:
- \(2x^2+9x+9\)
- \(6x^2+x−1\)
- Responda a
-
\((2x+3)(x+3)\)
- Resposta b
-
\((3x-1)(2x+1)\)
Fatorando um Trinômio Quadrado Perfeito
Um trinômio quadrado perfeito é um trinômio que pode ser escrito como o quadrado de um binômio. Lembre-se de que quando um binômio é quadrado, o resultado é o quadrado do primeiro termo somado ao dobro do produto dos dois termos e o quadrado do último termo.
\[a^2+2ab+b^2={(a+b)}^2\]
e
\[a^2-2ab+b^2={(a-b)}^2\]
Podemos usar essa equação para fatorar qualquer trinômio quadrado perfeito.
Um trinômio quadrado perfeito pode ser escrito como o quadrado de um binômio:
\[a^2+2ab+b^2=(a+b)^2\]
- Confirme se o primeiro e o último termo são quadrados perfeitos.
- Confirme se o médio prazo é o dobro do produto de\(ab\).
- Escreva o formulário fatorado como\({(a+b)}^2\).
Fator\(25x^2+20x+4\).
Solução
Observe isso\(25x^2\) e\(4\) são quadrados perfeitos porque\(25x^2={(5x)}^2\)\(4=2^2\) e. Em seguida, verifique se o termo intermediário é o dobro do produto de\(5x\)\(2\) e. O médio prazo é, de fato, o dobro do produto:\(2(5x)(2)=20x\). Portanto, o trinômio é um trinômio quadrado perfeito e pode ser escrito como\({(5x+2)}^2\).
Fator\(49x^2−14x+1\).
- Responda
-
\({(7x−1)}^2\)
Fatorando uma diferença de quadrados
A diferença de quadrados é um quadrado perfeito subtraído de um quadrado perfeito. Lembre-se de que uma diferença de quadrados pode ser reescrita como fatores contendo os mesmos termos, mas sinais opostos, porque os termos intermediários se cancelam quando os dois fatores são multiplicados.
\[a^2−b^2=(a+b)(a−b)\]
Podemos usar essa equação para fatorar quaisquer diferenças de quadrados.
Uma diferença de quadrados pode ser reescrita como dois fatores contendo os mesmos termos, mas sinais opostos.
\[a^2−b^2=(a+b)(a−b)\]
- Confirme se o primeiro e o último termo são quadrados perfeitos.
- Escreva o formulário fatorado como\((a+b)(a−b)\).
Fator\(9x^2−25\).
Solução
Observe isso\(9x^2\) e\(25\) são quadrados perfeitos porque\(9x^2={(3x)}^2\)\(25=5^2\) e. O polinômio representa uma diferença de quadrados e pode ser reescrito como\((3x+5)(3x−5)\).
Fator\(81y^2−100\).
- Responda
-
\((9y+10)(9y−10)\)
Não. A soma dos quadrados não pode ser fatorada.
Fatorando a soma e a diferença dos cubos
Agora, veremos dois novos produtos especiais: a soma e a diferença dos cubos. Embora a soma dos quadrados não possa ser fatorada, a soma dos cubos pode ser fatorada em um binômio e um trinômio.
\[a^3+b^3=(a+b)(a^2−ab+b^2)\]
Da mesma forma, a soma dos cubos pode ser fatorada em um binômio e um trinômio, mas com sinais diferentes.
\[a^3−b^3=(a−b)(a^2+ab+b^2)\]
Podemos usar a sigla SOAP para lembrar os sinais ao fatorar a soma ou a diferença dos cubos. A primeira letra de cada palavra está relacionada aos sinais: Mesmo oposto sempre positivo. Por exemplo, considere o exemplo a seguir.
\[x^3−2^3=(x−2)(x^2+2x+4)\]
O sinal dos primeiros 2 é o mesmo que o sinal entre\(x^3−2^3\). O signo do\(2x\) termo é oposto ao sinal entre\(x^3−2^3\). E o sinal do último termo,\(4\), é sempre positivo.
Podemos fatorar a soma de dois cubos como
\[a^3+b^3=(a+b)(a^2−ab+b^2)\]Podemos fatorar a diferença de dois cubos como
\[a^3−b^3=(a−b)(a^2+ab+b^2)\]
- Confirme se o primeiro e o último termo são cubos,\(a^3+b^3\) ou\(a^3−b^3\).
- Para uma soma de cubos, escreva a forma fatorada como\((a+b)(a^2−ab+b^2)\). Para uma diferença de cubos, escreva a forma fatorada como\((a−b)(a^2+ab+b^2)\).
Fator\(x^3+512\).
Solução
Observe isso\(x^3\) e\(512\) são cubos porque\(8^3=512\). Reescreva a soma dos cubos como\((x+8)(x^2−8x+64)\).
Análise
Depois de escrever a soma dos cubos dessa forma, podemos pensar que devemos verificar se a porção trinomial pode ser considerada mais adiante. No entanto, a porção trinomial não pode ser fatorada, portanto, não precisamos verificar.
Fator a soma dos cubos:\(216a^3+b^3\).
- Responda
-
\((6a+b)(36a^2−6ab+b^2)\)
Fator\(8x^3−125\).
Solução
Observe isso\(8x^3\) e\(125\) são cubos porque\(8x^3={(2x)}^3\)\(125=5^3\) e. Escreva a diferença dos cubos como\((2x−5)(4x^2+10x+25)\).
Análise
Assim como com a soma dos cubos, não poderemos fatorar ainda mais a porção trinomial.
Considere a diferença dos cubos:\(1000x^3−1\)
- Responda
-
\((10x−1)(100x^2+10x+1)\)
Fatoração de expressões com expoentes fracionários ou negativos
Expressões com expoentes fracionários ou negativos podem ser fatoradas retirando um GCF. Procure a variável ou o expoente que é comum a cada termo da expressão e retire essa variável ou expoente elevado à menor potência. Essas expressões seguem as mesmas regras de fatoração que aquelas com expoentes inteiros. Por exemplo,\(2x^{\tfrac{1}{4}}+5x^{\tfrac{3}{4}}\) pode ser considerado retirando\(x^{\tfrac{1}{4}}\) e sendo reescrito como\(x^{\tfrac{1}{4}}(2+5x^{\tfrac{1}{2}})\).
Fator\(3x{(x+2)}^{-\tfrac{1}{3}}+4{(x+2)}^{\tfrac{2}{3}}\).
Solução
Fator o termo com o menor valor do expoente. Nesse caso, isso seria\({(x+2)}^{-\tfrac{1}{3}}\).
\[\begin{align*} &(x+2)^{-\tfrac{1}{3}}(3x+4(x+2))\qquad \text{Factor out the GCF }\\ &(x+2)^{-\tfrac{1}{3}}(3x+4x+8)\qquad \text{Simplify } \\ &(x+2)^{-\tfrac{1}{3}}(7x+8) \end{align*}\]
Fator\(2{(5a−1)}^{\tfrac{3}{4}}+7a{(5a−1)}^{−\tfrac{1}{4}}\).
- Responda
-
\({(5a−1)}^{−\tfrac{1}{4}}(17a−2)\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com a fatoração de polinômios.
2. Fator Trinômios quando a é igual a 1
Equações-chave
| diferença de quadrados | \(a^2−b^2=(a+b)(a−b)\) |
| trinômio quadrado perfeito | \(a^2+2ab+b^2=(a+b)^2\) |
| soma dos cubos | \(a^3+b^3=(a+b)(a^2−ab+b^2)\) |
| diferença de cubos | \(a^3−b^3=(a−b)(a^2+ab+b^2)\) |
- O maior fator comum, ou GCF, pode ser fatorado a partir de um polinômio. A verificação de um GCF deve ser a primeira etapa em qualquer problema de fatoração. Veja o exemplo.
- Trinômios com coeficiente inicial 1 podem ser fatorados encontrando números que tenham um produto do terceiro termo e uma soma do segundo termo. Veja o exemplo.
- Os trinômios podem ser fatorados usando um processo chamado fatoração por agrupamento. Veja o exemplo.
- Trinômios quadrados perfeitos e a diferença de quadrados são produtos especiais e podem ser fatorados usando equações. Veja o exemplo e o exemplo.
- A soma dos cubos e a diferença dos cubos podem ser fatoradas usando equações. Veja o exemplo e o exemplo.
- Polinômios contendo expoentes fracionários e negativos podem ser fatorados retirando um GCF. Veja o exemplo.


