18.4: Movimento em duas e três dimensões

Last updated
Save as PDF

Page ID: 184895

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Verifique sua compreensão

4.1. (a) Tomando a derivada em relação ao tempo da função de posição, temos$\vec{v}$ (t) = 9,0t ²$\hat{i}$ e$\vec{v}$ (3,0s) = 81,0$\hat{i}$ m/s. (b) Como a função de velocidade não é linear, suspeitamos que a velocidade média não seja igual à velocidade instantânea. Verificamos isso e encontramos $$\ vec {v} _ {avg} =\ frac {\ vec {r} (t_ {2}) -\ vec {r} (t_ {1})} {t_ {2} - t_ {1}} =\ frac {\ vec {r} (4,0\; s) -\ vec {r} (2,0\; s)} {4.0\; s - 2.0\; s} =\ frac {(188.0\;\ hat {i} - 20,0\;\ hat {i})\; m} {2.0\; s} = 84,0\;\ hat {i}\; m/s, $$ que é diferente de$\vec{v}$ (3,0 s) = 81,0$\hat{i}$ m/s.

4.2. O vetor de aceleração é constante e não muda com o tempo. Se a, b e c não forem zero, a função de velocidade deve ser linear no tempo. Temos$\vec{v}$ (t) =$\int \vec{a}$ dt =$\int$ (a$\hat{i}$ + b$\hat{j}$ + c$\hat{k}$) dt = (a$\hat{i}$ + b$\hat{j}$ + c$\hat{k}$) t m/s, já que tomar a derivada da função de velocidade produz$\vec{a}$ (t). Se algum dos componentes da aceleração for zero, esse componente da velocidade seria uma constante.

4.3. (a) Escolha o topo do penhasco onde a rocha é lançada a partir da origem do sistema de coordenadas. Embora seja arbitrário, normalmente escolhemos o tempo t = 0 para corresponder à origem. (b) A equação que descreve o movimento horizontal é x = x ₀ + v _x t. Com x _{0 = 0}, essa equação se torna x = v _x t. (c) A equação 4.27 até a equação 4.29 e a equação 4.46 descrevem o movimento vertical, mas como y ₀ = 0 e v _0y = 0, essas equações simplificam muito para se tornar y =$\frac{1}{2}$ (v _0y _{+ v y}) t =$\frac{1}{2}$ v _y t, v _y = −gt, y = −$\frac{1}{2}$ gt ² e v _y ² = −2gy. (d) Usamos as equações cinemáticas para encontrar os componentes x e y da velocidade no ponto de impacto. Usando v _y ² = −2gy e observando que o ponto de impacto é −100,0 m, descobrimos que o componente y da velocidade no impacto é v _y = 44,3 m/s. Recebemos o componente _{x, v x} = 15,0 m/s, para que possamos calcular a velocidade total no impacto: v = 46,8 m/s e$\theta$ = 71,3° abaixo da horizontal.

4.4. O tiro de golfe a 30°.

4.5. 134,0 cm/s

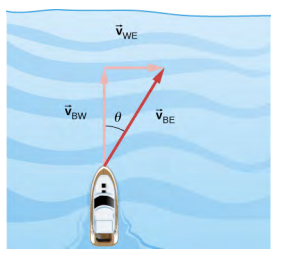
4.6. Rotulando subscritos para a equação vetorial, temos B = barco, R = rio e E = Terra. A equação vetorial se torna$\vec{v}_{BE}$ =$\vec{v}_{BR}$ +$\vec{v}_{RE}$. Temos a geometria do triângulo reto mostrada na figura abaixo. Resolvendo para$\vec{v}_{BE}$, temos $$v_ {BE} =\ sqrt {v_ {BR} ^ {2} + v_ {RE} ^ {2}} =\ sqrt {4.5^ {2} + 3.0^ {2}} $$$$v_ {BE} = 5,4\; m/s,\ quad\ theta =\ tan^ {-1}\ left (\ dfrac {3.0} {4.5}\ right) = 33,7^ {o}\ ldotp\]

Os vetores V sub B W, V sub W E e V sub B E formam um triângulo reto. Um barco é mostrado no vértice onde as caudas de V sub B W e V sub B E se encontram. O vetor V sub B W aponta para cima. V sub W E aponta para a direita. V sub B E aponta para cima e para a direita, em um ângulo com a vertical. V sub B E é a soma vetorial de v sub B W e V sub W E.

Perguntas conceituais

1. Linha reta

3. A inclinação deve ser zero porque o vetor de velocidade é tangente ao gráfico da função de posição.

5. Não, os movimentos nas direções perpendiculares são independentes.

7. a. Não; b. mínimo no ápice da trajetória e máximo no lançamento e impacto; c. não, a velocidade é um vetor; d. sim, onde pousa

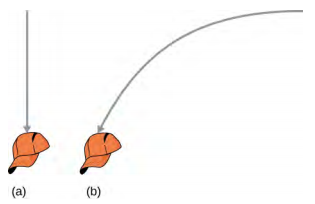
9. Ambos caíram no chão ao mesmo tempo.

11. Sim

13. Se ele vai passar a bola para outro jogador, ele precisa ficar de olho no quadro de referência no qual os outros jogadores da equipe estão localizados.

15.

Figura a: a trajetória de um chapéu é reta para baixo. Figura b: a trajetória de um chapéu é parabólica, curvando-se para baixo e para a esquerda.

Problemas

17. $\vec{r}$= 1,0$\hat{i}$ − 4,0$\hat{j}$ + 6,0$\hat{k}$

19. $\Delta \vec{r}_{Total}$= 472,0 m$\hat{i}$ + 80,3 m$\hat{j}$

21. Soma dos deslocamentos = −6,4 km$\hat{i}$ + 9,4 km$\hat{j}$

23. a.$\vec{v}$ (t) = 8,0 t$\hat{i}$ + 6,0 t ²$\hat{k}$,$\vec{v}$ (0) = 0,$\vec{v}$ (1,0) = 8,0$\hat{i}$ + 6,0$\hat{k}$ m/s

b.$\vec{v}_{avg}$ = 4,0$\hat{i}$ + 2,0$\hat{k}$ m/s

25. $\Delta \vec{r}_{1}$= 20,00 m$\hat{j}$,$\Delta \vec{r}_{2}$ = (2.000 x 10 ⁴ m) (cos 30°$\hat{i}$ + sin 30°$\hat{j}$),$\Delta \vec{r}$ = 1.700 x 10 ⁴ m$\hat{i}$ + 1.002 x 10 ⁴ m$\hat{j}$

27. a.$\vec{v}$ (t) = (4,0 t$\hat{i}$ + 3,0 t$\hat{j}$) m/s,$\vec{r}$ (t) = (2,0 t ²$\hat{i}$ +$\frac{3}{2}$ t ² m$\hat{j}$)

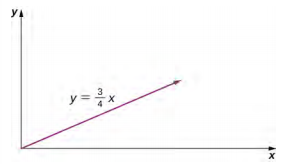
b. x (t) = 2,0t 2m, y (t) =$\frac{3}{2}$ t ² m, t ² =$\frac{x}{2} \Rightarrow$ y =$\frac{3}{4}$ x

Um gráfico da função linear y é igual a 3 quartos de x. O gráfico é uma linha reta de inclinação positiva que passa pela origem.

29. a.$\vec{v}$ (t) = (6,0 t$\hat{i}$ − 21,0 t ²$\hat{j}$ + 10,0 t ⁻³$\hat{k}$) m/s

b.$\vec{a}$ (t) = (6,0$\hat{i}$ − 42,0t$\hat{j}$ − 30t ⁻⁴$\hat{k}$) m/s ²

c.$\vec{v}$ (2,0s) = (12,0$\hat{i}$ − 84,0$\hat{j}$ + 1,25$\hat{k}$) m/s

d.$\vec{v}$ (1,0 s) = (6,0$\hat{i}$ − 21,0$\hat{j}$ + 10,0$\hat{k}$) m/s, |$\vec{v}$ (1,0 s) | = 24,0 m/s;$\vec{v}$ (3,0 s) = (18,0$\hat{i}$ − 189,0$\hat{j}$ + 0,37$\hat{k}$) m/s, |$\vec{v}$ (3,0 s) | = 190,0 m/s

e.$\vec{r}$ (t) = (3,0t ²$\hat{i}$ − 7,0t ³$\hat{j}$ − 5,0t ⁻²$\hat{k}$) cm,$\vec{v}_{avg}$ = (9,0$\hat{i}$ − 49,0$\hat{j}$ − 6,3$\hat{k}$) m/s

31. a.$\vec{v}$ (t) = −sin (1,0 t)$\hat{i}$ + cos (1,0 t)$\hat{j}$ +$\hat{k}$

b.$\vec{a}$ (t) = −cos (1,0 t)$\hat{i}$ − sin (1,0 t)$\hat{j}$

33. a. t = 0,55 s

b. x = 110 m

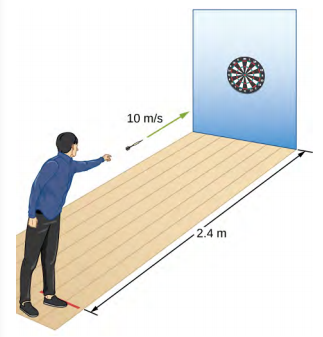
35. a. t = 0,24s, d = 0,28 m

b. Eles têm uma mira alta.

Uma ilustração de uma pessoa jogando um dardo. O dardo é lançado horizontalmente a uma distância de 2,4 metros do tabuleiro de dardos, nivelado com o alvo do tabuleiro de dardos, com uma velocidade de 10 metros por segundo.

37. a. t = 12,8 s, x = 5619 m

b. v _y = 125,0 m/s, v _x = 439,0 m/s, |$\vec{v}$ | = 456,0 m/s

39. a. v _y = v _0y − gt, t = 10s, v _y = 0, v _0y = 98,0 m/s, v ₀ = 196,0 m/s

b. h = 490,0 m

c. v _0x = 169,7 m/s, x = 3394,0 m

d. x = 2545,5 m, y = 367,5 m,$\vec{s}$ = 2545,5 m$\hat{i}$ + 367,5 m$\hat{j}$

41. −100 m = (−2,0 m/s) t − (4,9 m/s ²) t ², t = 4,3 s, x = 86,0 m

43. _Lua R = 48 m

45. a. v _0y = 24 m/s, v _y ² = v _0y ² − 2gy$\Rightarrow$ h = 23,4 m

b. t = 3 s, v _0x = 18 m/s, x = 54 m

c. y = −100 m, y ₀ = 0, y − y ₀ = v _0y, t −$\frac{1}{2}$ gt ² − 100 = 24t − 4,9t ²$\Rightarrow$ t = 7,58 s

d. x = 136,44 m

e.$$\ begin {split} t & = 2.0\; s, y = 28,4\; m, x = 36\; m\\ t & = 4,0\; s, y = 17,6\; m, x = 22,4\; m\\ t & = 6,0\; s, y = −32,4\; m, x = 108\; m\ end {split}\]

47. v _0y = 12,9 m/s, y − y ₀ = v _0y t −$\frac{1}{2}$ gt ² − 20,0 = 12,9t − 4,9t ²

t = 3,7 s, v _0x = 15,3 m/s$\Rightarrow$ x = 56,7 m

Assim, o chute do jogador cai 13,3 m abaixo do green.

49. a. R = 60,8 m

b. R = 137,8 m

51. a. v _y ² = v _0y ² − 2gy$\Rightarrow$ y = 2,9 m/s

y = 3,3 m/s

y =$\frac{v_{0y}^{2}}{2g}$$\frac{(v_{0} \sin \theta)^{2}}{2g} \Rightarrow \sin \theta$ = 0,91$\Rightarrow$$\theta$ = 65,5°

53. R = 18,5 m

55. y = (tan$\theta_{0}$) x −$\Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big]$ x ²$\Rightarrow$ v ₀ = 16,4 m/s

57. R$\frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \Rightarrow \theta_{0}$ = 15,0°

59. O wide receiver leva 1,1 s para cobrir os últimos 10 m de sua corrida.

T _tof$\frac{2(v_{0} \sin \theta)}{g} \Rightarrow \sin \theta$ = 0,27$\Rightarrow \theta$ = 15,6°

61. a _C = 40 m/s ²

63. a _C =$\frac{v^{2}}{r} \Rightarrow$ v ² = r, a _C = 78,4, v = 8,85 m/s

T = 5,68 s, que é 0,176 rev/s = 10,6 rev/min

65. Vênus está a 108,2 milhões de km do Sol e tem um período orbital de 0,6152 y.

r = 1,082 x 10 ¹¹ m, T = 1,94 x 10 ⁷ s

v = 3,5 x 10 ⁴ m/s, a _C = 1,135 x 10 ⁻² m/s ²

67. 360 rev/min = 6 rev/s

v = 3,8 m/s, a _C = 14,4 m/s ²

69. a. O' (t) = (4,0$\hat{i}$ + 3,0$\hat{j}$ + 5,0$\hat{k}$) t m

b.$\vec{r}_{PS}$ =$\vec{r}_{PS'}$ +$\vec{r}_{S'S}$,$\vec{r}$ (t) =$\vec{r′}$ (t) + (4,0$\hat{i}$ + 3,0$\hat{j}$ + 5,0$\hat{k}$) t m

c.$\vec{v}$ (t) =$\vec{v′}$ (t) + (4,0$\hat{i}$ + 3,0$\hat{j}$ + 5,0$\hat{k}$) m/s

d. As acelerações são as mesmas.

71. $\vec{v}_{PC}$= (2,0$\hat{i}$ + 5,0$\hat{j}$ + 4,0$\hat{k}$) m/s

73. a. A = ar, S = gaivota, G = solo

$\vec{v}_{SA}$= 9,0 m/s, velocidade da gaivota em relação ao ar parado

$\vec{v}_{AG}$=? ,$\vec{v}_{SG}$ = 5 m/s,$\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{AG} = \vec{v}_{SG} − \vec{v}_{SA}$

$\vec{v}_{AG}$= −4,0 m/s

b.$\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{SG}$ = −13,0 m/s

$\frac{−6000\; m}{−13.0\; m/s}$= 7 min 42 s

75. Pegue a direção positiva para ser a mesma direção em que o rio está fluindo, que é o leste. S = costa/terra, W = água e B = barco.

a.$\vec{v}_{BS}$ = 11 km/h, t = 8,2 min

b.$\vec{v}_{BS}$ = −5 km/h, t = 18 min

c.$\vec{v}_{BS} = \vec{v}_{BW} + \vec{v}_{WS}, \theta$ = 22° a oeste do norte

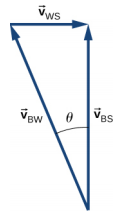
Os vetores V sub B W, V sub W S e V sub B S formam um triângulo reto, com V sub B W como hipotenusa. V sub B S aponta para cima. V sub W S aponta para a direita. V sub B W aponta para cima e para a esquerda, em um ângulo de teta em relação à vertical. V sub B S é a soma vetorial de v sub B W e V sub W S.

d. |$\vec{v}_{BS}$ | = 7,4 km/h, t = 6,5 min

e.$\vec{v}_{BS}$ = 8,54 km/h, mas apenas o componente da velocidade direto do outro lado do rio é usado para obter o tempo

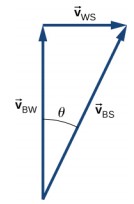
Os vetores V sub B W, V sub W S e V sub B S formam um triângulo reto, com V sub B S como hipotenusa. V sub B W aponta para cima. V sub W S aponta para a direita. V sub B S aponta para cima e para a direita, em um ângulo de teta em relação à vertical. V sub B S é a soma vetorial de v sub B W e V sub W S.

t = 6,0 min

A jusante = 0,3 km

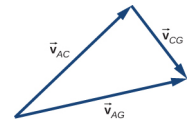
77. $\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}$

|$\vec{v}_{AC}$ | = 25 km/h, |$\vec{v}_{CG}$ | = 15 km/h, |$\vec{v}_{AG}$ | = 29,15 km/h,$\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}$

O ângulo entre$\vec{v}_{AC}$ e$\vec{v}_{AG}$ é 31°, então a direção do vento é 14° norte de leste.

Os vetores V sub A C, V sub C G e V sub A G formam um triângulo. V sub A C e V sub C G estão em ângulos retos. V sub A G é a soma vetorial de v sub A C e V sub C G.

Problemas adicionais

79. a _C = 39,6 m/s ²

81. 90,0 km/h = 25,0 m/s, 9,0 km/h = 2,5 m/s, 60,0 km/h = 16,7 m/s

a _T = −2,5 m/s ², a _C = 1,86 m/s ², a = 3,1 m/s ²

83. O raio do círculo de revolução na latitude$\lambda$ é R _E cos$\lambda$. A velocidade do corpo é$\frac{2 \pi r}{T}$. a _C =$\frac{4 \pi^{2} R_{E} \cos \lambda}{T^{2}}$ for$\lambda$ = 40°, a _C = 0,26% g

85. a _T = 3,00 m/s ²

v (5 s) = 15,00 m/s, a _C = 150,00 m/s ²,$\theta$ = 88,8° em relação à tangente ao círculo de revolução direcionado para dentro.

|$\vec{a}$ | = 150,03 m/s ²

87. $\vec{a}$(t) = −A$\omega^{2}$ cos$\omega$ t$\hat{i}$ − Um$\omega^{2}$ sin$\omega$ t$\hat{j}$

a _C = 5,0 m$\omega^{2}$,$\omega$ = 0,89 rad/s

$\vec{v}$(t) = −2,24 m/s$\hat{i}$ − 3,87 m/s$\hat{j}$

89. $\vec{r}_{1}$= 1,5$\hat{j}$ + 4,0$\hat{k}$,$\vec{r}_{2} = \Delta \vec{r} + \vec{r}_{1}$ = 2,5$\hat{i}$ + 4,7$\hat{j}$ + 2,8$\hat{k}$

91. v _x (t) = 265,0 m/s, v _y (t) = 20,0 m/s,$\vec{v}$ (5,0 s) = (265,0$\hat{i}$ + 20,0$\hat{j}$) m/s

93. R = 1,07 m

95. v ₀ = 20,1 m/s

97. v = 3072,5 m/s, a _C = 0,223 m/s ²

Problemas de desafio

99. a. −400,0 m = v _0y t − 4,9t ², 359,0 m = v _0x t, t =$\frac{359.0}{v_{0x}}$ − 400,0 = 359,0$\frac{v_{0y}}{v_{0x}}$ − 4,9$\left(\dfrac{359.0}{v_{0x}}\right)^{2}$

−400,0 = 359,0 do que 40 −$\frac{631,516.9}{v_{0x}^{2}} \Rightarrow$ v _0x ² = 900,6, v _0x = 30,0 m/s, v _0y = v _0x tan 40 = 25,2 m/s, v = 39,2 m/s

b. t = 12,0 s

101. a.$\vec{r}_{TC}$ = (−32 + 80t)$\hat{i}$ + 50t$\hat{j}$, |$\vec{r}_{TC}$ | ² = (−32 + 80t) ² + (50t) ²

2r$\frac{dr}{dt}$ = 2 (−32 + 80t) + 100t,$\frac{dr}{dt} = \frac{2(−32 + 80t) + 100t}{2r}$ = 0

260t = 64$\Rightarrow$ t = 15 min

b. |$\vec{r}_{TC}$ | = 17 km