Skip to main content
Global

18.3: Movimento ao longo de uma linha reta

  1. Last updated
  2. Save as PDF
  • Page ID
    184948

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Verifique sua compreensão

    3.1. (a) O deslocamento do ciclista é\(\Delta\) x = x f − x 0 = −1 km. (O deslocamento é negativo porque consideramos que o leste é positivo e o oeste é negativo.) (b) A distância percorrida é de 3 km + 2 km = 5 km. (c) A magnitude do deslocamento é de 1 km.

    3.2. (a) Tomando a derivada de x (t) dá v (t) = −6t m/s. (b) Não, porque o tempo nunca pode ser negativo. (c) A velocidade é v (1,0 s) = −6 m/s e a velocidade é |v (1,0 s) | = 6 m/s.

    3.3. Inserindo os conhecidos, temos\(\bar{a} = \frac{\Delta v}{\Delta t} = \frac{2.0 \times 10^{7}\; m/s − 0}{10^{−4}\; s − 0} = 2.0 \times 10^{11}\; m/s^{2}\).

    3.4. Se tomarmos o leste para ser positivo, o avião terá aceleração negativa porque está acelerando em direção ao oeste. Também está desacelerando; sua aceleração é oposta em direção à sua velocidade.

    3.5. Para responder isso, escolha uma equação que nos permita resolver o tempo t, considerando apenas a, v 0 e v$$v = v_ {0} + em\ ldotp$$ Reorganize para resolver para t: $$t =\ frac {v − v_ {0}} {a} =\ frac {400\; m/s − 0\; m/s} {20\; m/s^ {2} = 20 s\ ldotp\]

    3.6. a =\(\frac{2}{3}\) m/s 2.

    3.7. Demora 2,47 s para atingir a água. A quantidade de distância percorrida aumenta mais rapidamente.

    3.8. a. A função de velocidade é a integral da função de aceleração mais uma constante de integração. Pela equação 3,91, $$v (t) =\ int a (t) dt + C_ {1} =\ int (5 − 10t) dt + C_ {1} = 5t − 5t^ {2} + C_ {1}\ ldotp$$ Como v (0) = 0, temos C 1 = 0; então, $$v (t) = 5t − 5t^ {2}\ ldotp$$ b. Pela equação 3,93, $$x (t) =\ int v (t) dt + C_ {2} =\ int (5t − 5t^ {2}) dt + C_ {2} =\ frac {5} {2} t^ {2} −\ frac {5} {3} t^ {3} + C_ {2}\ ldotp$$ Como x (0) = 0, temos C 2 = 0 e $$x (t) =\ frac {5} {2} t^ {2} −\ frac {5} {3} t^ {3}\ ldotp$$ c. A velocidade pode ser escrita como v (t) = 5t (1 — t), que é igual a zero em t = 0, e t = 1 s.

    Perguntas conceituais

    1. Você dirige seu carro até a cidade e volta para passar pela sua casa até a casa de um amigo.

    3. Se as bactérias estão se movendo para frente e para trás, os deslocamentos estão se cancelando e o deslocamento final é pequeno.

    5. Distância percorrida

    7. A velocidade média é a distância total percorrida dividida pelo tempo decorrido. Se você for caminhar, sair e voltar para sua casa, sua velocidade média é um número positivo. Como a velocidade média = deslocamento/tempo decorrido, sua velocidade média é zero.

    9. Velocidade média. Eles são os mesmos se o carro não inverter a direção.

    11. Não, em uma dimensão, a velocidade constante requer aceleração zero.

    13. Uma bola é lançada no ar e sua velocidade é zero no ápice do lançamento, mas a aceleração não é zero.

    15. Mais, menos

    17. Se a aceleração, o tempo e o deslocamento forem os conhecidos e as velocidades inicial e final forem as incógnitas, então duas equações cinemáticas devem ser resolvidas simultaneamente. Além disso, se a velocidade, o tempo e o deslocamento finais forem os conhecidos, duas equações cinemáticas devem ser resolvidas para a velocidade e a aceleração iniciais.

    19. a. No topo de sua trajetória; b. sim, no topo de sua trajetória; c. sim

    21. Terra$$v = v_ {0} − gt = −gt; $$ Moon$$v′=\ frac {g} {6} t′$$ $v = v′− gt = −\ frac {g} {6} t′$$ $t′= 6t; $$ Terra $$y = −\ frac {1} {2} gt^ {2} $$ Lua $$ $y′= −\ frac {1} {2}\ frac {g} {6} (6t) ^ {2} = −\ frac {1} {2} g6t^ {2} = −6\ left (\ dfrac {1} {2} gt^ {2}\ direita) = −6y\]

    Problemas

    25. a.\(\vec{x}_{1}\) = (−2,0 m)\(\hat{i}\),\(\vec{x}_{2}\) = (5,0 m)\(\hat{i}\)

    b. 7.0 km a leste

    27. a. t = 2,0 s

    b. x (6,0) − x (3,0) = −8,0 − (−2,0) = −6,0 m

    29. a. 150,0 s,\(\vec{v}\) = 156,7 m/s

    b. 45,7% da velocidade do som ao nível do mar

    31.

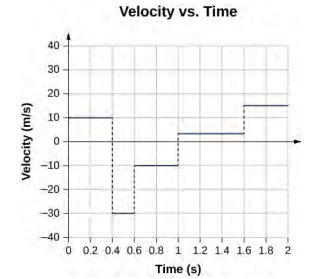
    O gráfico mostra a velocidade em metros por segundo plotada em função do tempo em segundos. A velocidade começa em 10 metros por segundo, diminui para -30 em 0,4 segundos; aumenta para -10 metros em 0,6 segundos, aumenta para 5 em 1 segundo, aumenta para 15 em 1,6 segundos.

    33.

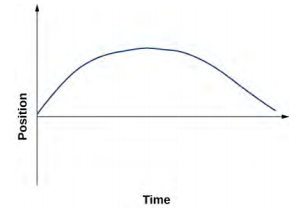
    O gráfico mostra a posição traçada versus o tempo. Começa na origem, aumenta atingindo o máximo e depois diminui perto de zero.

    35. a. v (t) = (10 − 4t) m/s; v (2 s) = 2 m/s, v (3 s) = −2 m/s

    b. |v (2 s) | = 2 m/s, |v (3 s) | = 2 m/s

    c.\(\bar{v}\) = 0 m/s

    37. a = 4,29 m/s 2

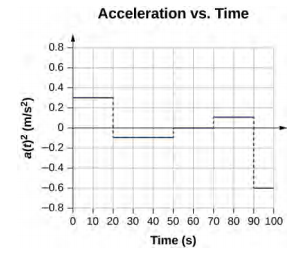
    39.

    O gráfico mostra a aceleração em metros por segundo ao quadrado representada graficamente versus o tempo em segundos. A aceleração é de 0,3 metros por segundo quadrado entre 0 e 20 segundos, -0,1 metros por segundo quadrado entre 20 e 50 segundos, zero entre 50 e 70 segundos, -0,6 entre 90 e 100 segundos.

    41. a = 11,1 g

    43. 150 m

    45. a. 525 mm

    b. v = 180 m/s

    47. uma.

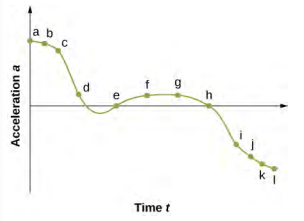
    O gráfico é um gráfico da aceleração a em função do tempo t. O gráfico não é linear, com a aceleração sendo positiva no início, negativa no final e cruzando o eixo x entre os pontos d e e e nos pontos e e h.

    b. A aceleração tem o maior valor positivo em t a c. A aceleração é zero em t e e t h d. A aceleração é negativa em t i, t j, t k, t l

    49. a. a = −1,3 m/s 2

    b. v 0 = 18 m/s

    c. t = 13,8 s

    51. v = 502,20 m/s

    53. uma.

    A figura mostra o objeto com velocidade igual a 0 metros por segundo e aceleração igual a 2,4 metros por segundo ao quadrado no ponto zero. Quando o tempo é igual a 12 segundos, a aceleração permanece igual a 2,4 metros por segundo. A velocidade e a posição do objeto são desconhecidas.

    b. Conhecidos: a = 2,40 m/s 2, t = 12,0 s, v 0 = 0 m/s e x 0 = 0 m; c. x = x 0 + v 0 t +\(\frac{1}{2}\) em 2 =\(\frac{1}{2}\) em 2 = 2,40 m/s 2 (12,0 s) 2 = 172,80 m, a resposta parece razoável em cerca de 172,8 m; d. v = 28,8 m/s

    55. uma.

    A figura mostra o objeto com velocidade zero e aceleração desconhecida no início. Depois de um tempo desconhecido, o objeto atinge a velocidade de 30 centímetros por segundo e está a uma distância de 1,8 centímetros do ponto de partida. A aceleração do objeto neste ponto é desconhecida.

    b. Conhecidos: v = 30,0 cm/s, x = 1,80 cm

    c. a = 250 cm/s 2, t = 0,12 s

    d. sim

    57. a. 6,87 m/s 2

    b. x = 52,26 m

    59. a. a = 8450 m/s 2

    b. t = 0,0077 s

    61. a. a = 9,18 g

    b. t = 6,67 x 10 −3 s

    c. a = −40,0 m/s 2, a = 4,08 g

    63. Conhecidos: x = 3 m, v = 0 m/s, v0 = 54 m/s. Queremos a, então podemos usar esta equação: a = −486 m/s 2.

    65. a. a = 32,58 m/s 2

    b. v = 161,85 m/s

    c. v > v max, porque a suposição de aceleração constante não é válida para um dragster. Um dragster muda de marcha e teria uma aceleração maior na primeira marcha do que na segunda marcha do que na terceira marcha, e assim por diante. A aceleração seria maior no início, então não estaria acelerando a 32,6 m/s 2 durante os últimos metros, mas substancialmente menor, e a velocidade final seria menor que 162 m/s.

    67. a. y = −8,23 m, v 1 = −18,9 m/s

    b. y = −18,9 m, v 2 = 23,8 m/s

    c. y = −32,0 m, v 3 = −28,7 m/s

    d. y = −47,6 m, v 4 = −33,6 m/s

    e. y = −65,6 m, v 5 = −38,5 m/s

    69. a. Conhecidos: a = −9,8 m/s 2, v 0 = −1,4 m/s, t = 1,8 s, y 0 = 0 m

    b. y = y 0 + v 0 t −\(\frac{1}{2}\) gt 2, y = v 0 t −\(\frac{1}{2}\) gt = −1,4 m/s (1,8 seg) −\(\frac{1}{2}\) (9,8) (1,8 s) 2 = −18,4 m e a origem está nos socorristas, que estão 18,4 m acima da água.

    71. a. v 2 = v 0 2 − 2g (y − y 0), y 0 = 0, v = 0, y =\(\frac{v_{0}^{2}}{2g}\) =\(\frac{(4.0 m/s)^{2}}{2(9.80)}\) = 0,82 m

    b. Para o ápice v = 0,41 s vezes 2 para a placa = 0,82 s do tabuleiro para a água y = y 0 + v 0 t −\(\frac{1}{2}\) gt 2, y = −1,80 m, y 0 = 0, v 0 = 4,0 m/s −1,8 = 4,0t − 4,9t 2, 4,9t 2 − 4,0t − 1,80 = 0, solução para equação quadrática dá 1,13 s

    c. v 2 = v 0 2 − 2g (y − y 0) y 0 = 0, v 0 = 4,0 m/s, y = −1,80 m, v = 7,16 m/s

    73. Tempo até o ápice: t = 1,12 s vezes 2 é igual a 2,24 s a uma altura de 2,20 m. A 1,80 m de altura é um adicional de 0,40 m.$$y = y_ {0} + v_ {0} t −\ frac {1} {2} gt^ {2} $$$y = −0,40\; m$$$y_ {0} = 0$$y $$$v_ {0} = −11,0\; m/s$$$$−0,40 = −11,0t − 4,9t^ {2}\; ou\; 4,9t^ {2} + 11,0t − 0,40 = 0\ ldotp$$ Pegue a raiz positiva, então o tempo para ir os 0,4 m adicionais é 0,04 s. O tempo total é 2,24 s + 0,04 s = 2,28 s.

    75. a. v 2 = v 0 2 − 2g (y − y 0), y 0 = 0, v = 0, y = 2,50 m, $$v_ {0} ^ {2} = 2gy\ Rightarrow v_ {0} =\ sqrt {2 (9,80) (2,50)} = 7,0\; m/s;\]

    b. t = 0,72 s vezes 2 dá 1,44 s no ar

    77. a. v = 70,0 m/s

    b. tempo ouvido após o início da queda da rocha: 0,75 s, tempo para chegar ao solo: 6,09 s

    79. a. A = m/s 2, B = m/s 5/2

    b. v (t) =\(\int\) a (t) dt + C 1 =\(\int\) (A − Bt 1/2) dt + C 1 = At −\(\frac{2}{3}\) Bt 3/2 + C 1\[v(0) = 0 = C_{1}\; so\; v(t_{0}) = At_{0} − \frac{2}{3} Bt_{0}^{3/2};\]

    c. x (t) =\(\int\) v (t) dt + C 2 =\(\int\) (Em −\ frac {2} {3}\) Bt 3 /2) dt + C 2 =\(\frac{1}{2}\) Em 2 −\(\frac{4}{15}\) Bt 5/2 + C 2\[x(0) = 0 = C_{2}\; so\; x(t_{0}) = \frac{1}{2} At_{0}^{2} − \frac{4}{15} Bt_{0}^{5/2}\]

    81. a. $$\ begin {split} a (t) & = 3,2 m/s^ {2}\ quad t\ leq 5.0\; s\\ a (t) & = 1,5\; m/s^ {2}\ quad 5.0\; s\ leq t\ leq 11.0\; s\\ a (t) & = 0\; m/s^ {2}\ quad\ quad t > 11.0 0\; s\ end {split}\]

    b. $$\ begin {split} x (t) & =\ int v (t) dt + C_ {2} =\ int 3.2tdt + C_ {2} = 1.6t^ {2} + C_ {2}\ quad t\ leq 5.0\; s\\ x (0) & = 0\ Rightarrow C_ {2} = 0\; portanto,\; x (2.0\; s) = 6,4\; m\\ x (t) & =\ int v (t) dt + C_ {2} =\ int [16,0 − 1,5 (t − 5,0)] dt + C_ {2} = 16t − 1,5\ esquerda (\ dfrac {t^ {2}} {2} − 5,0t\ direita) + C_ {2}\ quad 5.0\; s\ leq t\ leq 11.0\; s\\ x (5\; s) & = 1,6 (5,0) ^ {2} = 40\; m = 16 (5,0\; s) − 1,5\ left (\ dfrac {5^ {2}} {2} {2} − 5,0 (5,0)\ direita) + C_ {2}\ end {split} $$$$\ begin {split} 40 & = 98,75 + C_ {2}\ Rightarrow C_ {2} = −58,75\\ x (7,0 s) & = 16 (7,0) − 1,5\ left (\ dfrac {7^ {2}} {2} − 5,0 (7)\ direita) − 58. 75 = 69\; m\\ x (t) & =\ int 7.0dt + C_ {2} = 7t + C_ {2}\ quad t\ geq 11.0\; s\\ x (11,0\; s) & = 16 (11) − 1,5\ left (\ dfrac {11^ {2}} {2} − 5,0 (11)\ direita) − 58,75 = 109 = 7 (11,0\; s) + C_ {2}\ Rightarrow C_ {2} = 32\; m\\ x (t) & = 7t + 32\; m\ quad x\ geq 11.0\; s\ Flecha direita x (12,0\; s) = 7 (12) + 32 = 116\; m\ end {dividido}\]

    Problemas adicionais

    83. Siga para o oeste para ser a direção positiva. 1º avião:\(\bar{v}\) = 600 km/h; 2º avião:\(\bar{v}\) = 667,0 km/h

    85. a =\(\frac{v − v_{0}}{t − t_{0}}\), t = 0, a\(\frac{−3.4\; cm/s − v_{0}}{4\; s}\) = 1,2 cm/s 2\(\Rightarrow\) v 0 = − 8,2 cm/s, v = v 0 + em = − 8,2 + 1,2 t; v = −7,0 cm/s, v = −1,0 cm/s

    87. a = −3 m/s 2

    89. a. v = 8,7 x 10 5 m/s

    b. t = 7,8 x 10 −8 s

    91. 1 km = v 0 (80,0 s) +\(\frac{1}{2}\) a (80,0) 2; 2 km = v 0 (200,0) +\(\frac{1}{2}\) a (200,0) 2 resolva simultaneamente para obter a =\(− \frac{0.1}{2400.0}\) km/s 2 e v 0 = 0,014167 km/s, que é 51,0 km/h. A velocidade no final da viagem é v = 21,0 km/h.

    93. a = −0,9 m/s 2

    95. Equação para o carro em alta velocidade: Este carro tem uma velocidade constante, que é a velocidade média, e não está acelerando, então use a equação para deslocamento com x 0 = 0: x = x 0 +\(\bar{v}\) t =\(\bar{v}\) t; Equação para o carro da polícia: Este carro está acelerando, então use o equação para deslocamento com x 0 = 0 e v 0 = 0, já que o carro da polícia parte do repouso: x = x 0 + v 0 t +\(\frac{1}{2}\)\(\frac{1}{2}\) em 2 = em 2; Agora temos uma equação de movimento para cada carro com um parâmetro comum, que pode ser eliminado para encontrar a solução. Nesse caso, resolvemos para t. Etapa 1, eliminando x: x =\(\bar{v}\) t =\(\frac{1}{2}\) em 2; Etapa 2, resolvendo para t: t =\(\frac{2 \bar{v}}{a}\). O carro em alta velocidade tem uma velocidade constante de 40 m/s, que é sua velocidade média. A aceleração do carro da polícia é de 4 m/s 2. Avaliando t, o tempo até o carro da polícia chegar ao carro em alta velocidade, temos t\(\frac{2 \bar{v}}{a}\) =\(\frac{2(40)}{4}\) = = 20 s.

    97. Nessa aceleração, ela chega a uma parada completa em t =\(\frac{−v_{0}}{a}\) =\(\frac{8}{0.5}\) = 16 s, mas a distância percorrida é x = 8 m/s (16 s) −\(\frac{1}{2}\) (0,5) (16 s) 2 = 64 m, que é menor do que a distância que ela está longe da linha de chegada, então ela nunca termina a corrida.

    99. x 1 =\(\frac{3}{2}\) v 0 t; x 2 =\(\frac{5}{3}\) x 1

    101. v 0 = velocidade de 7,9 m/s na parte inferior da janela. v = 7,9 m/s; v 0 = 14,1 m/s

    103. a. v = 5,42 m/s

    b. v = 4,64 m/s

    c. a = 2874,28 m/s 2

    d. (x − x 0) = 5,11 x 10 −3 m

    105. Considere que os jogadores caem do repouso na altura de 1,0 m e 0,3 m. 0,9 s; 0,5 s

    107. a. t = 6,37 s tomando a raiz positiva

    b. v = 59,5 m/s

    109. a. y = 4,9 m

    b. v = 38,3 m/s; c. −33,3 m

    111. h =\(\frac{1}{2}\) gt 2, h = altura total e tempo para cair no chão\(\frac{2}{3}\) h =\(\frac{1}{2}\) g (t − 1) 2 em t — 1 segundo ele cai\(\frac{2}{3}\) h$$\ frac {2} {3}\ left (\ dfrac {1} {2} gt^ {2}\ right) =\ frac {1} {2} g (t − 1) ^ {2}\; ou\;\ frac {t^ {2}} {3} =\ frac {1} {2} (t − 1) ^ {2} $$$$0 = t^ {2} − 6t + 3,\; t =\ frac {6\ pm\ sqrt {62 − 4\ cdotp 3}} {2} = 3\ pm\ frac {\ sqrt {24}} {2} $$ t = 5,45 s e h = 145,5 m. A outra raiz tem menos de 1 s. Verifique se t = 4,45 s, h =\(\frac{1}{2}\) gt 2 = 97,0 m =\(\frac{2}{3}\) (145,5)

    Problemas de desafio

    113. a. v (t) = 10t − 12t 2 m/s, a (t) = 10 − 24t m/s 2

    b. v (2 s) = −28 m/s, a (2 s) = −38m/s 2

    c. A inclinação da função de posição é zero ou a velocidade é zero. Há duas soluções possíveis: t = 0, que dá x = 0, ou t\(\frac{10.0}{12.0}\) = 0,83 s, que dá x = 1,16 m. A segunda resposta é a escolha correta

    d. 0,83 s

    p. 1,16 mm

    115. 96 km/h = 26,67 m/s, a\(\frac{26.67\; m/s}{4.0\; s}\) = 6,67 m/s 2, 295,38 km/h = 82,05 m/s, t = 12,3 s tempo para acelerar até a velocidade máxima; x = 504,55 m = distância percorrida durante a aceleração; 7495,44 m a uma velocidade constante;\(\frac{7495.44\; m}{82.05\; m/s}\) = 91,35 s, então o tempo total é 91,35 s + 12,3 s = 103,65 s.