8.2: Energia potencial de um sistema
- Page ID
- 185446
- Relacione a diferença de energia potencial com o trabalho realizado em uma partícula para um sistema sem atrito ou resistência ao ar
- Explicar o significado do zero da função de energia potencial para um sistema
- Calcule e aplique a energia potencial gravitacional para um objeto próximo à superfície da Terra e a energia potencial elástica de um sistema de molas de massa
Em Work, vimos que o trabalho realizado em um objeto pela força gravitacional constante, próximo à superfície da Terra, sobre qualquer deslocamento é função apenas da diferença nas posições dos pontos finais do deslocamento. Essa propriedade nos permite definir um tipo de energia diferente para o sistema do que sua energia cinética, que é chamada de energia potencial. Consideramos várias propriedades e tipos de energia potencial nas subseções a seguir.
Noções básicas sobre energia potencial
Em Movimento em duas e três dimensões, analisamos o movimento de um projétil, como chutar uma bola de futebol na Figura\(\PageIndex{1}\). Neste exemplo, vamos ignorar o atrito e a resistência do ar. À medida que a bola sobe, o trabalho realizado pela força gravitacional na bola é negativo, porque o deslocamento da bola é positivo na vertical e a força devida à gravidade é negativa na vertical. Também observamos que a bola diminuiu a velocidade até atingir seu ponto mais alto no movimento, diminuindo assim a energia cinética da bola. Essa perda de energia cinética se traduz em um ganho na energia potencial gravitacional do sistema futebol-Terra.
À medida que a bola cai em direção à Terra, o trabalho realizado na bola agora é positivo, porque o deslocamento e a força gravitacional apontam verticalmente para baixo. A bola também acelera, o que indica um aumento na energia cinética. Portanto, a energia é convertida da energia potencial gravitacional de volta em energia cinética.
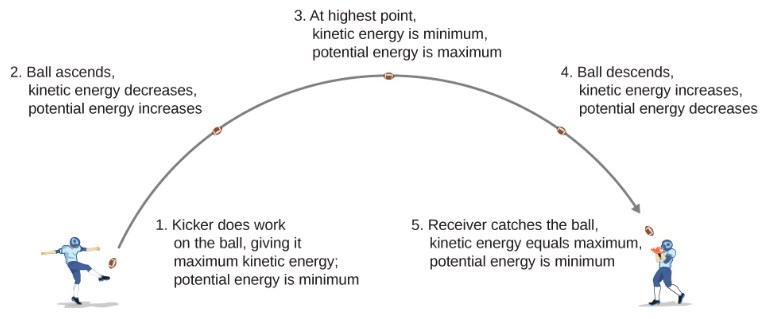
Com base nesse cenário, podemos definir a diferença de energia potencial do ponto A para o ponto B como o negativo do trabalho realizado:
\[ \Delta U_{A B}=U_{B}-U_{A}=-W_{A B} \label{8.1} \]
Essa fórmula afirma explicitamente uma diferença de energia potencial, não apenas uma energia potencial absoluta. Portanto, precisamos definir energia potencial em uma determinada posição de forma a declarar valores padrão de energia potencial por conta própria, em vez de possíveis diferenças de energia. Fazemos isso reescrevendo a função de energia potencial em termos de uma constante arbitrária,
\[ \Delta U=U(\overrightarrow{\mathbf{r}})-U\left(\overrightarrow{\mathbf{r}}_{0}\right) \label{8.2} \]
A escolha da energia potencial em um local de partida de\(\vec{r}_0\) é feita por conveniência no problema em questão. Mais importante ainda, qualquer escolha feita deve ser declarada e mantida consistente em todo o problema. Existem algumas opções bem aceitas de energia potencial inicial. Por exemplo, a altura mais baixa em um problema geralmente é definida como energia potencial zero ou, se um objeto estiver no espaço, o ponto mais distante do sistema geralmente é definido como energia potencial zero. Então, a energia potencial, em relação a zero em\(\vec{r}_0\), é justa\(U(\vec{r})\).
Enquanto não houver atrito ou resistência do ar, a mudança na energia cinética do futebol é igual a negativa da mudança na energia potencial gravitacional do futebol. Isso pode ser generalizado para qualquer energia potencial:
\[\Delta K_{A B}=-\Delta U_{A B} \label{8.3}\]
Vejamos um exemplo específico, escolhendo energia potencial zero para energia potencial gravitacional em pontos convenientes.
Uma partícula se move ao longo do eixo x sob a ação de uma força dada por F = -ax 2, onde a = 3 N/m 2. (a) Qual é a diferença em sua energia potencial à medida que ela se move de x A = 1 m para x B = 2 m? (b) Qual é a energia potencial da partícula em x = 1 m em relação a um dado 0,5 J de energia potencial em x = 0?
Estratégia
(a) A diferença na energia potencial é o negativo do trabalho realizado, conforme definido pela Equação\ ref {8.1}. O trabalho é definido no capítulo anterior como o produto escalar da força com a distância. Como a partícula está avançando na direção x, o produto escalar se simplifica para uma multiplicação (\(\hat{i} \cdot \hat{i}\)= 1). Para encontrar o trabalho total realizado, precisamos integrar a função entre os limites dados. Após a integração, podemos declarar o trabalho ou a mudança na energia potencial. (b) A função de energia potencial, em relação a zero em x = 0, é a integral indefinida encontrada na parte (a), com a constante de integração determinada pela Equação\ ref {8.3}. Em seguida, substituímos o valor x na função de energia potencial para calcular a energia potencial em x = 1.
Solução
a. O trabalho realizado pela força dada à medida que a partícula se move da coordenada x para x + dx em uma dimensão é
\[d W=\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=F d x=-a x^{2} d x \nonumber \]
Substituindo essa expressão na Equação\ ref {8.1}, obtemos
\[\Delta U=-W=\int_{x_{1}}^{x_{2}} a x^{2} d x=\left.\frac{1}{3}\left(3 \: \mathrm{N} / \mathrm{m}^{2}\right) x^{3}\right|_{1 \mathrm{m}} ^{2\mathrm{m}}=7 \: \mathrm{J} \nonumber \]
b. A integral indefinida para a função de energia potencial na parte (a) é
\[U(x)=\frac{1}{3} a x^{3}+\text { const. }, \nonumber \]
e queremos que a constante seja determinada por
\[ U(0) = 0.5 \: J. \nonumber \]
Assim, a energia potencial em relação a zero em x = 0 é apenas
\[U(x)=\frac{1}{3} a x^{3}+0.5 \: \mathrm{J} \nonumber \]
Portanto, a energia potencial em x = 1 m é
\[U(1 \: \mathrm{m})=\frac{1}{3}\left(3 \: \mathrm{N} / \mathrm{m}^{2}\right)(1 \: \mathrm{m})^{3}+0.5 \: \mathrm{J}=1.5 \: \mathrm{J}. \nonumber \]
Significância
Neste exemplo unidimensional, qualquer função que possamos integrar, independente do caminho, é conservadora. Observe como aplicamos a definição de diferença de energia potencial para determinar a função de energia potencial em relação a zero em um ponto escolhido. Observe também que a energia potencial, conforme determinada na parte (b), em x = 1 m é U (1 m) = 1 J e em x = 2 m é U (2 m) = 8 J; sua diferença é o resultado na parte (a).
No exemplo\(\PageIndex{1}\), quais são as energias potenciais da partícula em x = 1 m e x = 2 m em relação a zero em x = 1,5 m? Verifique se a diferença de energia potencial ainda é de 7 J.
Sistemas de várias partículas
Em geral, um sistema de interesse pode consistir em várias partículas. A diferença na energia potencial do sistema é o negativo do trabalho realizado pelas forças gravitacionais ou elásticas, que, como veremos na próxima seção, são forças conservadoras. A diferença de energia potencial depende apenas das posições inicial e final das partículas e de alguns parâmetros que caracterizam a interação (como massa para gravidade ou a constante de mola para a força da lei de Hooke).
É importante lembrar que a energia potencial é uma propriedade das interações entre objetos em um sistema escolhido, e não apenas uma propriedade de cada objeto. Isso é especialmente verdadeiro para forças elétricas, embora nos exemplos de energia potencial que consideramos abaixo, partes do sistema sejam tão grandes (como a Terra, em comparação com um objeto em sua superfície) ou tão pequenas (como uma mola sem massa), que as mudanças pelas quais essas partes sofrem são insignificantes quando incluídas no sistema.
Tipos de energia potencial
Para cada tipo de interação presente em um sistema, você pode rotular um tipo correspondente de energia potencial. A energia potencial total do sistema é a soma das energias potenciais de todos os tipos. (Isso decorre da propriedade aditiva do produto escalar na expressão do trabalho realizado.) Vejamos alguns exemplos específicos de tipos de energia potencial discutidos no Work. Primeiro, consideramos cada uma dessas forças quando agimos separadamente e depois quando ambas agem juntas.
Energia potencial gravitacional perto da superfície da Terra
O sistema de interesse consiste em nosso planeta, a Terra, e uma ou mais partículas próximas à sua superfície (ou corpos pequenos o suficiente para serem considerados partículas, em comparação com a Terra). A força gravitacional em cada partícula (ou corpo) é apenas seu peso mg próximo à superfície da Terra, atuando verticalmente para baixo. De acordo com a terceira lei de Newton, cada partícula exerce uma força na Terra de igual magnitude, mas na direção oposta. A segunda lei de Newton nos diz que a magnitude da aceleração produzida por cada uma dessas forças na Terra é mg dividida pela massa da Terra. Como a razão entre a massa de qualquer objeto comum e a massa da Terra é extremamente pequena, o movimento da Terra pode ser completamente negligenciado. Portanto, consideramos esse sistema um grupo de sistemas de partículas únicas, sujeitos à força gravitacional uniforme da Terra.
No Trabalho, o trabalho realizado em um corpo pela força gravitacional uniforme da Terra, próximo à sua superfície, dependia da massa do corpo, da aceleração devida à gravidade e da diferença de altura que o corpo percorreu, conforme dada pela Equação 7.2.4. Por definição, este trabalho é o negativo da diferença na energia potencial gravitacional, então essa diferença é
\[\Delta U_{\mathrm{grav}}=-W_{\mathrm{grav}, A B}=m g\left(y_{B}-y_{A}\right) \label{8.4}.\]
Você pode ver a partir disso que a função de energia potencial gravitacional, próxima à superfície da Terra, é
\[U(y)=m g y+\text { const. } \label{8.5}\]
Você pode escolher o valor da constante, conforme descrito na discussão da Equação\ ref {8.2}; no entanto, para resolver a maioria dos problemas, a constante mais conveniente a ser escolhida é zero para quando y = 0, que é a posição vertical mais baixa do problema.
O cume do Great Blue Hill em Milton, MA, está 147 m acima de sua base e tem uma elevação acima do nível do mar de 195 m (Figura\(\PageIndex{2}\)). (Seu nome nativo americano, Massachusetts, foi adotado pelos colonos por nomear a Colônia da Baía e o estado próximo à sua localização.) Um caminhante de 75 kg sobe da base até o cume. Qual é a energia potencial gravitacional do sistema Hiker-Earth em relação à energia potencial gravitacional zero na altura da base, quando o caminhante está (a) na base da colina, (b) no cume e (c) no nível do mar, posteriormente?
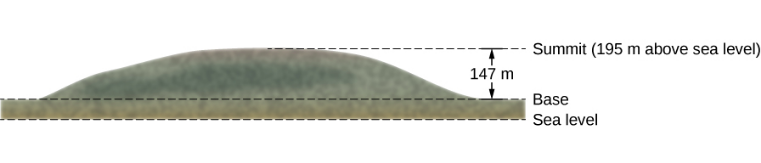
Estratégia
Primeiro, precisamos escolher uma origem para o eixo y e depois determinar o valor da constante que torna a energia potencial zero na altura da base. Em seguida, podemos determinar as energias potenciais a partir da Equação\ ref {8.5}, com base na relação entre a altura zero da energia potencial e a altura em que o caminhante está localizado.
Solução
a. Vamos escolher a origem do eixo y na altura da base, onde também queremos que seja o zero da energia potencial. Essa escolha torna a constante igual a zero e
\[U(\text { base })=U(0)=0 \nonumber\]
b. No cume, y = 147 m, então
\[ U(\text { summit }) = U(147 \: \mathrm{m})=m g h=(75 \times 9.8 \: \mathrm{N})(147 \: \mathrm{m})=108 \: \mathrm{kJ}. \nonumber \]
c. Ao nível do mar, y = (147 - 195) m = -48 m, então
\[ U \text { (sea-level) }=(75 \times 9.8 \mathrm{N})(-48 \mathrm{m})=-35.3 \mathrm{kJ} .\nonumber \]
Significância
Além de ilustrar o uso da Equação\ ref {8.4} e da Equação\ ref {8.5}, os valores da energia potencial gravitacional que encontramos são razoáveis. A energia potencial gravitacional é maior no cume do que na base e menor no nível do mar do que na base. A gravidade também funciona em você quando você sobe! Ele faz um trabalho negativo e não tanto (em magnitude) quanto seus músculos. Mas certamente funciona. Da mesma forma, seus músculos funcionam na descida, como um trabalho negativo. Os valores numéricos das energias potenciais dependem da escolha de zero da energia potencial, mas as diferenças fisicamente significativas da energia potencial não. [Observe que, como a Equação\ ref {8.2} é uma diferença, os valores numéricos não dependem da origem das coordenadas.]
Quais são os valores da energia potencial gravitacional do caminhante na base, no cume e no nível do mar, em relação a um zero de energia potencial no nível do mar?
Energia potencial elástica
Em Work, vimos que o trabalho realizado por uma mola perfeitamente elástica, em uma dimensão, depende apenas da constante da mola e dos quadrados dos deslocamentos da posição não esticada, conforme dado na Equação 7.2.5. Este trabalho envolve apenas as propriedades de uma interação com a lei de Hooke e não as propriedades de molas reais e quaisquer objetos que estejam ligados a elas. Portanto, podemos definir a diferença de energia potencial elástica para uma força de mola como o negativo do trabalho realizado pela força da mola nesta equação, antes de considerarmos sistemas que incorporam esse tipo de força. Assim,
\[\Delta U=-W_{A B}=\frac{1}{2} k\left(x_{B}^{2}-x_{A}^{2}\right) \label{8.6} \]
onde o objeto viaja do ponto A ao ponto B. A função de energia potencial correspondente a essa diferença é
\[U(x)=\frac{1}{2} k x^{2}+\text { const. } \label{8.7} \]
Se a força da mola for a única força atuando, é mais simples obter o zero da energia potencial em x = 0, quando a mola está em seu comprimento não esticado. Então, a constante é Equação\ ref {8.7} é zero. (Outras opções podem ser mais convenientes se outras forças estiverem atuando.)
Um sistema contém uma mola perfeitamente elástica, com um comprimento não esticado de 20 cm e uma constante de mola de 4 N/cm. (a) Quanta energia potencial elástica a mola contribui quando seu comprimento é de 23 cm? (b) Quanto mais energia potencial ela contribui se seu comprimento aumentar para 26 cm?
Estratégia
Quando a mola está em seu comprimento não esticado, ela não contribui em nada para a energia potencial do sistema, então podemos usar a Equação\ ref {8.7} com a constante igual a zero. O valor de x é o comprimento menos o comprimento não esticado. Quando a mola é expandida, o deslocamento da mola ou a diferença entre seu comprimento relaxado e o comprimento esticado deve ser usado para o valor x no cálculo da energia potencial da mola.
Solução
- O deslocamento da mola é x = 23 cm − 20 cm = 3 cm, então a energia potencial contribuída é U =\(\frac{1}{2}\) kx 2 =\(\frac{1}{2}\) (4 N/cm) (3 cm) 2 = 0,18 J.
- Quando o deslocamento da mola é x = 26 cm − 20 cm = 6 cm, a energia potencial é U =\(\frac{1}{2}\) kx 2 =\(\frac{1}{2}\) (4 N/cm) (6 cm) 2 = 0,72 J, que é um aumento de 0,54-J sobre a quantidade na parte (a).
Significância
O cálculo da energia potencial elástica e das diferenças de energia potencial da Equação\ ref {8.7} envolve resolver as energias potenciais com base nos comprimentos fornecidos da mola. Como U depende de x 2, a energia potencial para uma compressão (x negativo) é a mesma de uma extensão de igual magnitude.
Quando o comprimento da mola no Exemplo 8.2.3 muda de um valor inicial de 22,0 cm para um valor final, a energia potencial elástica que ela contribui muda em −0,0800J. Encontre o comprimento final.
Energia potencial gravitacional e elástica
Um sistema simples que incorpora os tipos gravitacionais e elásticos de energia potencial é um sistema vertical unidimensional de mola de massa. Isso consiste em uma partícula maciça (ou bloco), pendurada em uma extremidade de uma mola perfeitamente elástica e sem massa, cuja outra extremidade é fixa, conforme ilustrado na Figura\(\PageIndex{3}\).
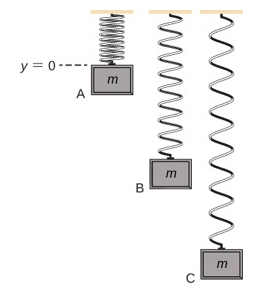
Primeiro, vamos considerar a energia potencial do sistema. Precisamos definir a constante na função de energia potencial da Equação\ ref {8.5}. Freqüentemente, o solo é uma escolha adequada para quando a energia potencial gravitacional é zero; no entanto, neste caso, o ponto mais alto ou quando y = 0 é uma localização conveniente para energia potencial gravitacional zero. Observe que essa escolha é arbitrária e o problema pode ser resolvido corretamente, mesmo que outra escolha seja escolhida.
Também devemos definir a energia potencial elástica do sistema e a constante correspondente, conforme detalhado na Equação\ ref {8.7}. É aqui que a mola não está esticada ou na posição y = 0.
Se considerarmos que a energia total do sistema está conservada, então a energia no ponto A é igual ao ponto C. O bloco é colocado apenas na mola, então sua energia cinética inicial é zero. Pela configuração do problema discutido anteriormente, tanto a energia potencial gravitacional quanto a energia potencial elástica são iguais a zero. Portanto, a energia inicial do sistema é zero. Quando o bloco chega ao ponto C, sua energia cinética é zero. No entanto, agora tem energia potencial gravitacional e energia potencial elástica. Portanto, podemos resolver a distância y que o bloco percorre antes de parar:
\ [\ begin {alinhado}
K_ {\ mathrm {A}} &+U_ {A} =K_ {C} +U_ {\ mathrm {C}}\\
0 &=0+m g y_ {C} +\ frac {1} {2} k\ esquerda (y_ {C}\ direita) ^ {2}\\ y_ {\ mathrm {C}\ direita) ^ {2}\\
y_ {\ mathrm {C}\}} &=\ frac {-2 m g} {k}
\ end {alinhado}\]

Um bloco pesando 1,2 N é pendurado em uma mola com uma constante de mola de 6,0 N/m, conforme mostrado na Figura\(\PageIndex{3}\). (a) Qual é a expansão máxima da mola, conforme visto no ponto C? (b) Qual é a energia potencial total no ponto B, a meio caminho entre A e C? (c) Qual é a velocidade do bloco no ponto B?
Estratégia
Na parte (a) calculamos a distância y C conforme discutido no texto anterior. Então, na parte (b), usamos metade do valor y para calcular a energia potencial no ponto B usando as equações Equação\ ref {8.4} e Equação\ ref {8.6}. Essa energia deve ser igual à energia cinética, Equação 7.3.1, no ponto B, já que a energia inicial do sistema é zero. Ao calcular a energia cinética no ponto B, agora podemos calcular a velocidade do bloco no ponto B.
Solução
a. Como a energia total do sistema é zero no ponto A, conforme discutido anteriormente, a expansão máxima da mola é calculada para ser:
\ begin {matriz} {l}
y_ {\ mathrm {C}} =\ frac {-2 m g} {k}\\
y_ {\ mathrm {C}} =\ frac {-2 (1,2\:\ mathrm {N})} {(6.0\:\ mathrm {N}/\ mathrm {m})} =-0,40\:\ mathrm {m})} =-0,40\:\ mathrm {M})} =-0,40\:\ mathrm {M}) {m}
\ end {matriz}
b. A posição de y B é metade da posição em y C ou -0,20 m. A energia potencial total no ponto B seria, portanto:
\ begin {alinhado}
U_ {B} &=m g y_ {B} +\ left (\ frac {1} {2} k y_ {B}\ direita) ^ {2}\
U_ {B} & =( 1.2\:\ mathrm {N}) (-0,20\:\ mathrm {m}) +\ frac {1} {2} (\ 6:\ mathrm {N}/\ mathrm {m}) (-0,20\:\ mathrm {m}) ^ {2}\\
U_ {B} &=-0,12\:\ mathrm {J}
\ end {alinhado}
c. A massa do bloco é o peso dividido pela gravidade.
\[m=\frac{F_{w}}{g}=\frac{1.2 \: \mathrm{N}}{9.8 \: \mathrm{m} / \mathrm{s}^{2}}=0.12 \: \mathrm{kg} \nonumber \]
A energia cinética no ponto B, portanto, é 0,12 J porque a energia total é zero. Portanto, a velocidade do bloco no ponto B é igual a
\ begin {matriz} {l}
K=\ frac {1} {2} m v^ {2}\\
v=\ sqrt {\ frac {2 K} {m}} =\ sqrt {\ frac {2 (0,12\:\ mathrm {J})} {(0,12\:\ mathrm {kg})}} =1,4\:\ mathrm {m}/\ mathrm {s}
\ end {matriz}
Significância
Mesmo que a energia potencial devido à gravidade seja relativa a um local zero escolhido, as soluções para esse problema seriam as mesmas se os pontos de energia zero fossem escolhidos em locais diferentes.
Suponha que a massa na Equação\ ref {8.6} seja dobrada, mantendo todas as outras condições iguais. A expansão máxima da primavera aumentaria, diminuiria ou permaneceria a mesma? A velocidade no ponto B seria maior, menor ou a mesma em comparação com a massa original?
Veja esta simulação para aprender sobre conservação de energia com um skatista! Construa pistas, rampas e saltos para o patinador e veja a energia cinética, a energia potencial e o atrito enquanto ele se move. Você também pode levar o skatista para diferentes planetas ou até mesmo para o espaço!
Um gráfico de amostra de uma variedade de energias é mostrado na Tabela\(\PageIndex{1}\) para dar uma ideia sobre os valores típicos de energia associados a determinados eventos. Alguns deles são calculados usando energia cinética, enquanto outros são calculados usando quantidades encontradas em uma forma de energia potencial que pode não ter sido discutida neste momento.
| Objeto/fenômeno | Energia em joules |
|---|---|
| Grande explosão | 10 68 |
| Uso anual mundial de energia | 4,0 x 10 20 |
| Bomba de fusão grande (9 megaton) | 3,8 x 10 16 |
| Bomba de fissão do tamanho de Hiroshima (10 quiloton) | 4,2 x 10 13 |
| 1 barril de petróleo bruto | 5,9 x 10 9 |
| 1 tonelada TNT | 4,2 x 10 9 |
| 1 galão de gasolina | 1,2 x 10 8 |
| Ingestão diária de alimentos para adultos (recomendada) | 1,2 x 10 7 |
| Carro de 1000 kg a 90 km/h | 3,1 x 10 5 |
| Bola de tênis a 100 km/h | 22 |
| Mosquito (10 −2 g a 0,5 m/s) | 1,3 x 10 -6 |
| Único elétron em um feixe de tubo de TV | 4,0 x 10 -15 |
| Energia para quebrar uma fita de DNA | 10 -19 |


