16.4: Energia transportada por ondas eletromagnéticas
- Page ID
- 184760
Ao final desta seção, você poderá:
- Expresse a densidade de energia média temporal das ondas eletromagnéticas em termos de suas amplitudes de campo elétrico e magnético
- Calcule o vetor Poynting e a intensidade de energia das ondas eletromagnéticas
- Explique como a energia de uma onda eletromagnética depende de sua amplitude, enquanto a energia de um fóton é proporcional à sua frequência
Qualquer pessoa que tenha usado um forno de microondas sabe que há energia nas ondas eletromagnéticas. Às vezes, essa energia é óbvia, como no calor do sol de verão. Outras vezes, é sutil, como a energia não sentida dos raios gama, que pode destruir as células vivas.
As ondas eletromagnéticas trazem energia para um sistema em virtude de seus campos elétricos e magnéticos. Esses campos podem exercer forças e mover cargas no sistema e, assim, trabalhar neles. No entanto, há energia na própria onda eletromagnética, seja ela absorvida ou não. Uma vez criados, os campos transportam energia para longe de uma fonte. Se alguma energia for absorvida posteriormente, as intensidades do campo diminuirão e tudo o que sobrar será acionado.
Claramente, quanto maior a intensidade dos campos elétrico e magnético, mais trabalho eles podem fazer e maior a energia que a onda eletromagnética carrega. Nas ondas eletromagnéticas, a amplitude é a intensidade máxima do campo elétrico e magnético (Figura\(\PageIndex{1}\)). A energia da onda é determinada pela amplitude da onda.
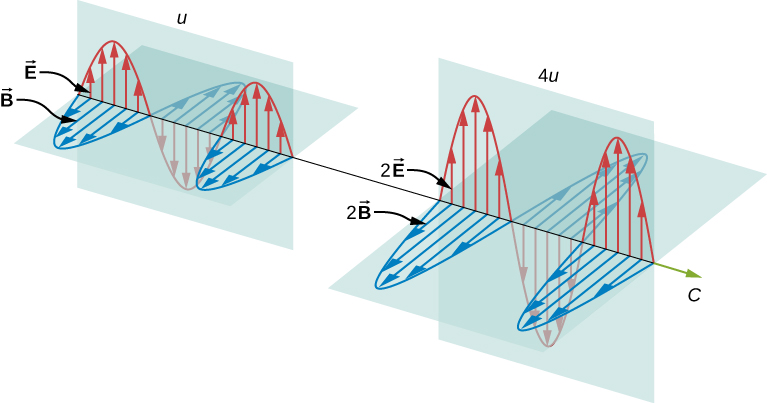
Para uma onda plana viajando na direção do eixo x positivo com a fase da onda escolhida de forma que o máximo da onda esteja na origem em\(t = 0\), os campos elétrico e magnético obedecem às equações
\[E_y (x,t) = E_0 \, \cos \, (kx - \omega t)\]
\[B_x (x,t) = B_0 \, \cos \, (kx - \omega t).\]
A energia em qualquer parte da onda eletromagnética é a soma das energias dos campos elétrico e magnético. Essa energia por unidade de volume, ou densidade de energia u, é a soma da densidade de energia do campo elétrico e da densidade de energia do campo magnético. Expressões para ambas as densidades de energia de campo foram discutidas anteriormente (\(u_E\)em Capacitância e\(u_B\) em Indutância). Combinando essas contribuições, obtemos
\[u (x,t) = u_E + u_B = \frac{1}{2}\epsilon_0 E^2 + \frac{1}{2\mu_0} B^2.\]
A expressão\(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}}B\) então mostra que a densidade de energia magnética\(u_B\) e a densidade de energia elétrica\(u_E\) são iguais, apesar do fato de que campos elétricos variáveis geralmente produzem apenas pequenos campos magnéticos. A igualdade das densidades de energia elétrica e magnética leva a
\[u(x,t) = \epsilon_0 E^2 = \frac{B^2}{\mu_0}. \label{16.27}\]
A densidade de energia se move com os campos elétrico e magnético de maneira semelhante às próprias ondas.
Podemos determinar a taxa de transporte de energia considerando um pequeno intervalo de tempo\(\Delta t\). Conforme mostrado na Figura\(\PageIndex{2}\), a energia contida em um cilindro de comprimento\(c\Delta t\) e área da seção transversal A passa pelo plano da seção transversal no intervalo\(\Delta t\).
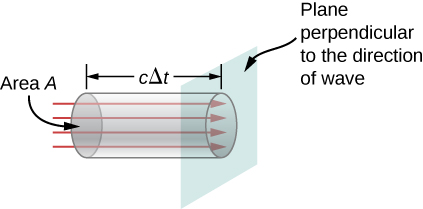
A energia que passa pela área\(A\) no tempo\(\Delta t\) é
\[u \times volume = uAc\Delta t.\]
A energia por unidade de área por unidade de tempo passando por um plano perpendicular à onda, chamado fluxo de energia e denotado por\(S\), pode ser calculada dividindo-se a energia pela área\(A\) e pelo intervalo de tempo\(\Delta t\).
\[S = \frac{\text{Energy passing area } A \text{ in time } \Delta t}{A \Delta t} = uc = \epsilon_0cE^2 = \frac{1}{\mu_0} EB.\]
De forma mais geral, o fluxo de energia através de qualquer superfície também depende da orientação da superfície. Para levar em consideração a direção, introduzimos um vetor\(\vec{S}\), chamado vetor Poynting, com a seguinte definição:
\[\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}.\]
O produto cruzado de\(\vec{E}\) e\(\vec{B}\) aponta na direção perpendicular a ambos os vetores. Para confirmar que a direção de\(\vec{S}\) é a da propagação da onda, e não sua negativa, retorne à Figura 16.3.2. Observe que as leis de Lenz e Faraday implicam que quando o campo magnético mostrado está aumentando no tempo, o campo elétrico é maior em\(x\) do que em\(x + \Delta x\). O campo elétrico está diminuindo com o aumento\(x\) no momento e local determinados. A proporcionalidade entre campos elétricos e magnéticos exige que o campo elétrico aumente no tempo junto com o campo magnético. Isso só é possível se a onda estiver se propagando para a direita no diagrama; nesse caso, as orientações relativas mostram que\(\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}\) está especificamente na direção da propagação da onda eletromagnética.
O fluxo de energia em qualquer lugar também varia no tempo, como pode ser visto substituindo\(u\) a Equação 16.3.19 pela Equação\ ref {16.27}.
\[S(x, t) = c\epsilon_0 E_0^2 \cos^2 \, (kx - \omega t) \label{16.29} \]
Como a frequência da luz visível é muito alta, da ordem de\(10^{14} \, Hz\), o fluxo de energia da luz visível em qualquer área é uma quantidade extremamente variável. A maioria dos dispositivos de medição, incluindo nossos olhos, detecta apenas uma média em muitos ciclos. A média temporal do fluxo de energia é a intensidade\(I\) da onda eletromagnética e é a potência por unidade de área. Ela pode ser expressa calculando a média da função cosseno na Equação\ ref {16.29} ao longo de um ciclo completo, que é o mesmo que calcular a média do tempo em muitos ciclos (aqui,\(T\) há um período):
\[I = S_{avg} = c\epsilon_0E_0^2 \frac{1}{T} \int_0^T \cos^2 \, \left(2\pi \frac{t}{T}\right) dt \label{16.30}.\]
Podemos avaliar a integral, ou então observar que, como o seno e o cosseno diferem meramente na fase, a média em um ciclo completo para\(cos^2 \, (\xi)\) é a mesma que para\(sin^2 \, (\xi)\), para obter
\[\langle \cos^2 \xi \rangle = \frac{1}{2} [\langle \cos^2 \xi \rangle + \langle \sin^2 \xi \rangle ] = \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
onde os colchetes angulares\(\langle . . . \rangle \) representam a operação de cálculo da média de tempo. A intensidade da luz se movendo\(c\) em velocidade no vácuo é então considerada
\[I = S_{avg} = \frac{1}{2}c\epsilon_0 E_0^2 \label{16.31}\]
em termos da intensidade máxima do campo elétrico\(E_0\), que também é a amplitude do campo elétrico. A manipulação algébrica produz a relação
\[I = \frac{cB_0^2}{2\mu_0} \label{16.32}\]
onde\(B_0\) está a amplitude do campo magnético, que é igual à intensidade máxima do campo magnético. Mais uma expressão para\(I_{avg}\) em termos de intensidade de campo elétrico e magnético é útil. Substituindo o fato de que\(cB_0 = E_0\), a expressão anterior se torna
\[I = \frac{E_0B_0}{2\mu_0} \label{16.33}.\]
Podemos usar qualquer uma das três equações anteriores que seja mais conveniente, porque as três equações são, na verdade, apenas versões diferentes do mesmo resultado: A energia em uma onda está relacionada à amplitude quadrada. Além disso, como essas equações são baseadas na suposição de que as ondas eletromagnéticas são senoidais, o pico de intensidade é o dobro da intensidade média; ou seja,\(I_0 = 2I\).
O feixe de um pequeno laser de laboratório normalmente tem uma intensidade de aproximadamente\(1.0 \times 10^{-3} W/m^2\). Supondo que o feixe seja composto por ondas planas, calcule as amplitudes dos campos elétrico e magnético no feixe.
Estratégia
Use a equação que expressa a intensidade em termos de campo elétrico para calcular o campo elétrico a partir da intensidade.
Solução
Da Equação\ ref {16.31}, a intensidade do feixe de laser é
\[I = \frac{1}{2}c\epsilon_0 E_0^2. \nonumber\]
A amplitude do campo elétrico é, portanto,
\[ \begin{align*} E_0 &= \sqrt{\frac{2}{c\epsilon_0}I} \\[4pt] &= \sqrt{\frac{2}{(3.00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}\left(1.0 \times 10^{-3} W/m^2 \right)} \\[4pt] &= 0.87 \, V/m. \end{align*}\]
A amplitude do campo magnético pode ser obtida a partir de:
\[B_0 = \frac{E_0}{c} = 2.9 \times 10^{-9} \, T. \nonumber\]
Uma lâmpada emite 5,00 W de potência como luz visível. Quais são os campos elétricos e magnéticos médios da luz a uma distância de 3,0 m?
Estratégia
Suponha que a potência de saída P da lâmpada esteja distribuída uniformemente sobre uma esfera de raio de 3,0 m para calcular a intensidade e, a partir dela, o campo elétrico.
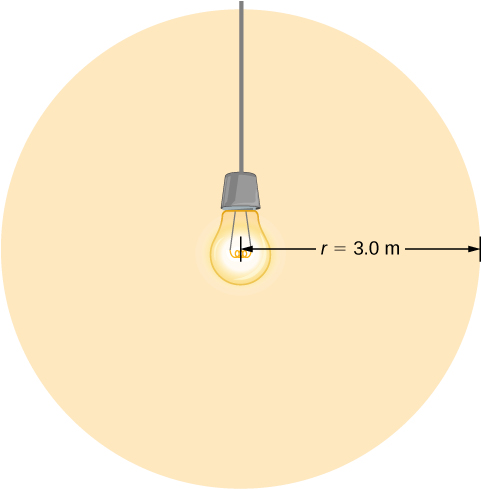
Solução
A energia irradiada como luz visível é então
\(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},\)
\(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3.0 \, m)^2 (3.00 \times 10^8 \, m/s)(8.85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1.92 \times 10^{-8} \, T\).
Significance
The intensity I falls off as the distance squared if the radiation is dispersed uniformly in all directions.
A 60-kW radio transmitter on Earth sends its signal to a satellite 100 km away (Figure \(\PageIndex{3}\)). At what distance in the same direction would the signal have the same maximum field strength if the transmitter’s output power were increased to 90 kW?
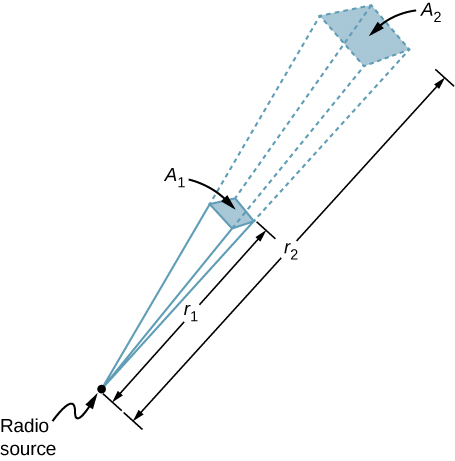
Strategy
The area over which the power in a particular direction is dispersed increases as distance squared, as illustrated in Figure \(\PageIndex{3}\). Change the power output P by a factor of (90 kW/60 kW) and change the area by the same factor to keep \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}\) the same. Then use the proportion of area A in the diagram to distance squared to find the distance that produces the calculated change in area.
Solution
Using the proportionality of the areas to the squares of the distances, and solving, we obtain from the diagram
\[ \begin{align*} \frac{r_2^2}{r_1^2} &= \frac{A_2}{A_1} = \frac{90 \, W}{60 \, W}, \\[4pt] r_2 &= \sqrt{\frac{90}{60}}(100 \, km) \\[4pt] &= 122 \, km. \end{align*}\]
Significance
The range of a radio signal is the maximum distance between the transmitter and receiver that allows for normal operation. In the absence of complications such as reflections from obstacles, the intensity follows an inverse square law, and doubling the range would require multiplying the power by four.


