16.3: Ondas eletromagnéticas planas
- Page ID
- 184733
Ao final desta seção, você poderá:
- Descreva como as equações de Maxwell predizem as direções relativas dos campos elétricos e magnéticos e a direção de propagação das ondas eletromagnéticas planas
- Explique como as equações de Maxwell preveem que a velocidade de propagação das ondas eletromagnéticas no espaço livre é exatamente a velocidade da luz
- Calcule a magnitude relativa dos campos elétrico e magnético em uma onda plana eletromagnética
- Descreva como as ondas eletromagnéticas são produzidas e detectadas
As ondas mecânicas viajam por um meio, como uma corda, água ou ar. Talvez a previsão mais significativa das equações de Maxwell seja a existência de campos elétricos e magnéticos (ou eletromagnéticos) combinados que se propagam pelo espaço como ondas eletromagnéticas. Como as equações de Maxwell se mantêm no espaço livre, as ondas eletromagnéticas previstas, diferentemente das ondas mecânicas, não precisam de um meio para sua propagação.
Um tratamento geral da física das ondas eletromagnéticas está além do escopo deste livro didático. Podemos, no entanto, investigar o caso especial de uma onda eletromagnética que se propaga pelo espaço livre ao longo do eixo x de um determinado sistema de coordenadas.
Ondas eletromagnéticas em uma direção
Uma onda eletromagnética consiste em um campo elétrico, definido como de costume em termos da força por carga em uma carga estacionária, e um campo magnético, definido em termos da força por carga em uma carga em movimento. Supõe-se que o campo eletromagnético seja uma função apenas da coordenada x e do tempo. O componente y do campo elétrico é então escrito como\(E_y (x,t)\), o componente z do campo magnético como\(B_z (x,t)\), etc. Como estamos assumindo espaço livre, não há cargas ou correntes livres, então podemos definir\(Q_{in} = 0\) e\(I = 0\) nas equações de Maxwell.
A natureza transversal das ondas eletromagnéticas
Examinamos primeiro o que a lei de Gauss para campos elétricos implica sobre as direções relativas do campo elétrico e a direção de propagação em uma onda eletromagnética. Suponha que a superfície gaussiana seja a superfície de uma caixa retangular cuja seção transversal é um quadrado do lado l e cujo terceiro lado tem comprimento\(\Delta x\), conforme mostrado na Figura\(\PageIndex{1}\). Como o campo elétrico é uma função somente de x e t, o componente y do campo elétrico é o mesmo tanto na parte superior (rotulada como Lado 2) quanto na parte inferior (rotulada como Lado 1) da caixa, de modo que essas duas contribuições para o fluxo são canceladas. O argumento correspondente também vale para o fluxo líquido do componente z do campo elétrico através dos lados 3 e 4. Qualquer fluxo líquido através da superfície, portanto, vem inteiramente do componente x do campo elétrico. Como o campo elétrico não tem dependência de y ou z,\(E_x(x,t)\) é constante na face da caixa com a área A e tem um valor possivelmente diferente\(E_x (x + \Delta x, t)\) que é constante na face oposta da caixa.
A aplicação da lei de Gauss dá
\[\text{Net flux} = - E_x (x,t) A + E_x (x + \Delta x, t) A = \dfrac{Q_{in}}{\epsilon_0} \label{16.13}\]
onde\(A = l \times l\) está a área das faces frontal e traseira da superfície retangular. Mas a carga incluída é\(Q_{in} = 0\), então o fluxo líquido desse componente também é zero, e a Equação\ ref {16.13} implica\(E_x (x,t) = E_x (x + \Delta x, t)\) em qualquer um\(\Delta x\). Portanto, se houver um componente x do campo elétrico, ele não poderá variar com x. Um campo uniforme desse tipo seria meramente sobreposto artificialmente à onda itinerante, por exemplo, por ter um par de placas com carga paralela. Esse componente não\(E_x(x,t)\) faria parte de uma onda eletromagnética se propagando ao longo do eixo x; então,\(E_x(x,t) = 0\) para essa onda. Portanto, os únicos componentes diferentes de zero do campo elétrico são\(E_y(x,t)\) e são\(E_z(x,t)\) perpendiculares à direção de propagação da onda.
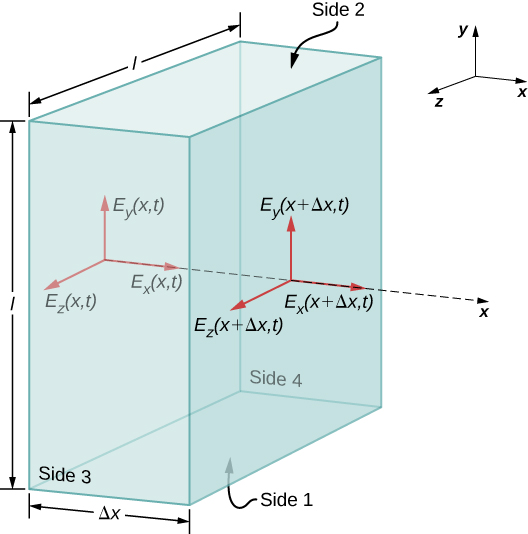
A similar argument holds by substituting E for B and using Gauss’s law for magnetism instead of Gauss’s law for electric fields. This shows that the B field is also perpendicular to the direction of propagation of the wave. The electromagnetic wave is therefore a transverse wave, with its oscillating electric and magnetic fields perpendicular to its direction of propagation.
The speed of propagation of electromagnetic waves
We can next apply Maxwell’s equations to the description given in connection with Figure 16.2.3 in the previous section to obtain an equation for the E field from the changing B field, and for the B field from a changing E field. We then combine the two equations to show how the changing E and B fields propagate through space at a speed precisely equal to the speed of light.
First, we apply Faraday’s law over Side 3 of the Gaussian surface, using the path shown in Figure \(\PageIndex{2}\). Because \(E_x(x,t) = 0\), we have
\[\oint \vec{E} \cdot d\vec{s} = - E_y(x,t)l + E_y(x + \Delta x,t)l.\]
Assuming \(\Delta x\) is small and approximating \(E_y (x + \Delta x,t)\) by
\[E_y (x + \Delta x,t) = E_y (x,t) + \dfrac{\partial E_y(x,t)}{\partial x} \Delta x,\]
we obtain
\[\oint \vec{E} \cdot d\vec{s} = \dfrac{\partial E_y (x,t)}{\partial x} (l\Delta x).\]
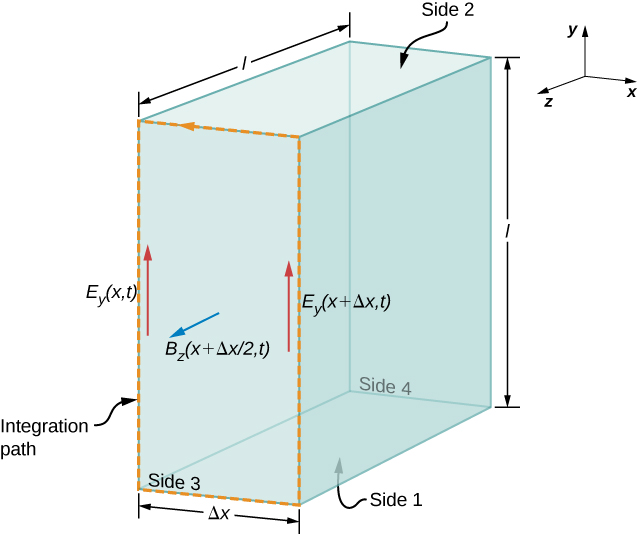
Por\(\Delta x\) ser pequeno, o fluxo magnético através da face pode ser aproximado por seu valor no centro da área percorrida, ou seja,\(B_z\left(x + \dfrac{\Delta x}{2}, t\right)\). O fluxo do campo B através da Face 3 é então o campo B vezes a área,
\[\oint_S \vec{B} \cdot \vec{n} dA = B_z \left(x + \dfrac{\Delta x}{2}, t\right) (l \Delta x). \label{16.14}\]
Da lei de Faraday,
\[\oint \vec{E} \cdot d\vec{s} = -\dfrac{d}{dt} \int_S \vec{B} \cdot \vec{n} dA.\label{16.15}\]
Portanto, a partir das Equações\ ref {16.13} e\ ref {16.14},
\[\dfrac{\partial E_y (x,t)}{\partial x} (l \Delta x) = - \dfrac{\partial}{\partial t} \left[ B_z \left( x + \dfrac{\Delta x}{2}, t\right) \right] (l\Delta x).\]
Cancelando\(l \Delta x\) e assumindo o limite\(\Delta x = 0\), pois ficamos com
\[\dfrac{\partial E_y (x,t)}{\partial x} = - \dfrac{\partial B_z(x,t)}{\partial t}. \label{16.16}\]
Poderíamos ter aplicado a lei de Faraday na superfície superior (numerada 2) na Figura\(\PageIndex{2}\), para obter a equação resultante
\[\dfrac{\partial B_z(x,t)}{\partial t} = - \dfrac{\partial E_y (x,t)}{\partial x}. \label{16.17}\]
Esta é a equação que descreve o campo E espacialmente dependente produzido pelo campo B dependente do tempo.
Em seguida, aplicamos a lei de Ampère-Maxwell (com\(I = 0\)) sobre as mesmas duas faces (Superfície 3 e depois Superfície 2) da caixa retangular da Figura\(\PageIndex{2}\). Aplicando a equação 16.2.16,
\[\oint \vec{B} \cdot d\vec{s} = \mu_0 \epsilon_0 (d/dt) \int_S \vec{E} \cdot n \, da\]
para a Superfície 3 e, em seguida, para a Superfície 2, produz as duas equações
\[\dfrac{\partial E_y (x,t)}{\partial x} = - \epsilon_0 \mu_0 \dfrac{\partial E_z (x,t)}{\partial t}, \label{16.18}\]
e
\[\dfrac{\partial B_z(x,t)}{\partial x} = - \epsilon_0 \mu_0 \dfrac{\partial E_y (x,t)}{\partial t}. \label{16.19}\]
Essas equações descrevem o campo B espacialmente dependente produzido pelo campo E dependente do tempo.
Em seguida, combinamos as equações que mostram a mudança do campo B produzindo um campo E com a equação que mostra a mudança do campo E produzindo um campo B. Tomando a derivada da Equação\ ref {16.16} em relação a x e usando a Equação\ ref {16.26} dá
\[\dfrac{\partial^2E_y}{\partial x^2} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial E_y}{\partial x}\right) = - \dfrac{\partial}{\partial x}\left(\dfrac{\partial B_z}{\partial t}\right) = - \dfrac{\partial}{\partial t}\left(\dfrac{\partial B_z}{\partial x}\right) = \dfrac{\partial}{\partial t}\left(\epsilon_0 \mu_0 \dfrac{\partial E_y}{\partial t}\right)\]
ou
\[\dfrac{\partial^2E_y}{\partial x^2} = \epsilon_0 \mu_0 \dfrac{\partial^2 E_y}{\partial t^2}\]
Essa é a forma assumida pela equação geral da onda para nossa onda plana. Como as equações descrevem uma onda viajando a uma velocidade c ainda não especificada, podemos supor que os componentes do campo são funções de x — ct para a onda que viaja na direção + x, ou seja,
\[E_y (x,t) = f(\xi) \, where \, \xi = x - ct. \label{16.21}\]
É deixado como um exercício matemático mostrar, usando a regra da cadeia para diferenciação, que as equações\ ref {16.17} e\ ref {16.18} implicam
\[1 = \epsilon_0 \mu_0 c^2.\]
A velocidade da onda eletromagnética no espaço livre é, portanto, dada em termos de permeabilidade e permissividade do espaço livre por
\[c = \dfrac{1}{\sqrt{\epsilon_0\mu_0}}. \label{16.22}\]
Poderíamos facilmente ter assumido uma onda eletromagnética com componentes de campo\(E_z (x,t)\)\(B_y (x,t)\) e. O mesmo tipo de análise com a Equação\ ref {16.25} e\ ref {16.24} também mostraria que a velocidade de uma onda eletromagnética é\(c = 1/\sqrt{\epsilon_0\mu_0}\).
A física dos campos eletromagnéticos itinerantes foi elaborada por Maxwell em 1873. Ele mostrou de uma forma mais geral do que a nossa derivação que as ondas eletromagnéticas sempre viajam no espaço livre com uma velocidade dada pela Equação\ ref {16.18}. Se avaliarmos a velocidade\(c = \dfrac{1}{\sqrt{\epsilon_0\mu_0}}\), descobrimos que
\[c = \dfrac{1}{\sqrt{\left(8.85 \times 10^{-12} \dfrac{C^2}{N \cdot m^2}\right)\left(4\pi \times 10^{-7} \dfrac{T \cdot m}{A}\right)}} = 3.00 \times 10^8 m/s,\]
que é a velocidade da luz. Imagine a empolgação que Maxwell deve ter sentido quando descobriu essa equação! Ele havia encontrado uma conexão fundamental entre dois fenômenos aparentemente não relacionados: campos eletromagnéticos e luz.
A equação da onda foi obtida (1) encontrando o campo E produzido pela mudança do campo B, (2) encontrando o campo B produzido pela mudança do campo E e combinando os dois resultados. Qual das equações de Maxwell foi a base da etapa (1) e qual da etapa (2)?
- Resposta (etapa 1)
-
Lei de Faraday
- Resposta (etapa 2)
-
a lei Ampère-Maxwell
Como os campos E e B estão relacionados
Até agora, vimos que as taxas de variação de diferentes componentes dos campos E e B estão relacionadas, que a onda eletromagnética é transversal e que a onda se propaga na velocidade c. A seguir, mostramos o que as equações de Maxwell implicam sobre a razão das magnitudes dos campos E e B e as direções relativas dos campos E e B.
Agora consideramos soluções para a Equação\ ref {16.16} na forma de ondas planas para o campo elétrico:
\[E_y(x,t) = E_0 \, \cos \, (kx - \omega t). \label{16.23}\]
Pegamos arbitrariamente a onda para viajar na direção +x e escolhemos sua fase para que a intensidade máxima do campo ocorra na origem no momento\(t = 0\). Somos justificados em considerar apenas senos e cossenos dessa maneira e generalizar os resultados, porque o teorema de Fourier implica que podemos expressar qualquer onda, incluindo até mesmo funções de passo quadrado, como uma superposição de senos e cossenos.
Em qualquer ponto específico do espaço, o campo E oscila senoidalmente na frequência angular\(\omega\) entre\(+E_0\) e\(-E_0\) e da mesma forma, o campo B oscila entre\(+B_0\)\(-B_0\) e. A amplitude da onda é o valor máximo de\(E_y(x,t)\). O período de oscilação T é o tempo necessário para uma oscilação completa. A frequência f é o número de oscilações completas por unidade de tempo e está relacionada à frequência angular\(\omega\) by\(\omega = 2\pi f\). O comprimento de onda\(\lambda\) é a distância percorrida por um ciclo completo da onda, e o número de onda k é o número de comprimentos de onda que se encaixam em uma distância de\(2\pi\) nas unidades que estão sendo usadas. Essas quantidades estão relacionadas da mesma forma que em uma onda mecânica:
\[\omega = 2\pi f, \, \, f = \dfrac{1}{T}, \, \, k = \dfrac{2\pi}{\lambda}, \, \, and \, \, c = f\lambda = \omega/k.\]
Dado que a solução de\(E_y\) tem a forma mostrada na Equação\ ref {16.20}, precisamos determinar o\(B\) campo que a acompanha. A partir da Equação\ ref {16.24}, o componente do campo magnético\(B_z\) deve obedecer
\[\dfrac{\partial B_z}{\partial t} = - \dfrac{\partial E_y}{\partial x}\]
\[\dfrac{\partial B_z}{\partial t} = - \dfrac{\partial}{\partial x} E_0 \, \cos \, (kx - \omega t) = kE_0 \, sin\, (kx - \omega t). \label{16.24}\]
Como a solução para o padrão de campo B da onda se propaga na direção + x na mesma velocidade c do padrão de campo E, ela deve ser uma função de\(k(x - ct) = kx - \omega t\). Assim, concluímos da Equação\ ref {16.21} que\(B_z\) é
\[B_z(x,t) = \dfrac{k}{\omega} E_0 \, \cos \, (kx - \omega t) = \dfrac{1}{c}E_0 \, \cos \, (kx - \omega t).\]
Esses resultados podem ser escritos como
\[E_y(x,t) = E_0 \, \cos \, (kx - \omega t)\]
\[B_z(x,t) = B_0 \, \cos \, (kx - \omega t) \label{16.25}\]
\[\dfrac{E_y}{B_z} = \dfrac{E_0}{B_0} = c. \label{16.26}\]
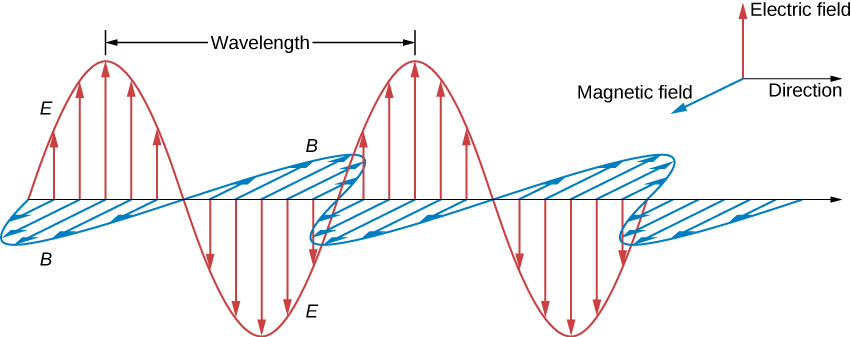
Portanto, os picos dos campos E e B coincidem, assim como os vales da onda, e em cada ponto, os campos E e B estão na mesma proporção igual à velocidade da luz c. A onda plana tem a forma mostrada na Figura\(\PageIndex{3}\).
What is the maximum strength of the B field in an electromagnetic wave that has a maximum E-field strength of 1000 V/m?
Strategy
To find the B-field strength, we rearrange Equation \ref{16.23} to solve for \(B\), yielding
\[B = \dfrac{E}{c}. \nonumber\]
Solution We are given E, and c is the speed of light. Entering these into the expression for B yields
\[B = \dfrac{1000 \, V/m}{3.00 \times 10^8 \, m/s} = 3.33 \times 10^{-6} T. \nonumber\]
Significance
The B-field strength is less than a tenth of Earth’s admittedly weak magnetic field. This means that a relatively strong electric field of 1000 V/m is accompanied by a relatively weak magnetic field.
Changing electric fields create relatively weak magnetic fields. The combined electric and magnetic fields can be detected in electromagnetic waves, however, by taking advantage of the phenomenon of resonance, as Hertz did. A system with the same natural frequency as the electromagnetic wave can be made to oscillate. All radio and TV receivers use this principle to pick up and then amplify weak electromagnetic waves, while rejecting all others not at their resonant frequency.
What conclusions did our analysis of Maxwell’s equations lead to about these properties of a plane electromagnetic wave:
- the relative directions of wave propagation, of the E field, and of B field,
- the speed of travel of the wave and how the speed depends on frequency, and
- the relative magnitudes of the E and B fields.
- Answer a
-
The directions of wave propagation, of the E field, and of B field are all mutually perpendicular.
- Answer b
-
The speed of the electromagnetic wave is the speed of light \(c = 1/\sqrt{\epsilon_0\mu_0}\) independent of frequency.
- Answer c
-
The ratio of electric and magnetic field amplitudes is \(E/B = c\).
Production and Detection of Electromagnetic Waves
A steady electric current produces a magnetic field that is constant in time and which does not propagate as a wave. Accelerating charges, however, produce electromagnetic waves. An electric charge oscillating up and down, or an alternating current or flow of charge in a conductor, emit radiation at the frequencies of their oscillations. The electromagnetic field of a dipole antenna is shown in Figure \(\PageIndex{4}\). The positive and negative charges on the two conductors are made to reverse at the desired frequency by the output of a transmitter as the power source. The continually changing current accelerates charge in the antenna, and this results in an oscillating electric field a distance away from the antenna. The changing electric fields produce changing magnetic fields that in turn produce changing electric fields, which thereby propagate as electromagnetic waves. The frequency of this radiation is the same as the frequency of the ac source that is accelerating the electrons in the antenna. The two conducting elements of the dipole antenna are commonly straight wires. The total length of the two wires is typically about one-half of the desired wavelength (hence, the alternative name half-wave antenna), because this allows standing waves to be set up and enhances the effectiveness of the radiation.
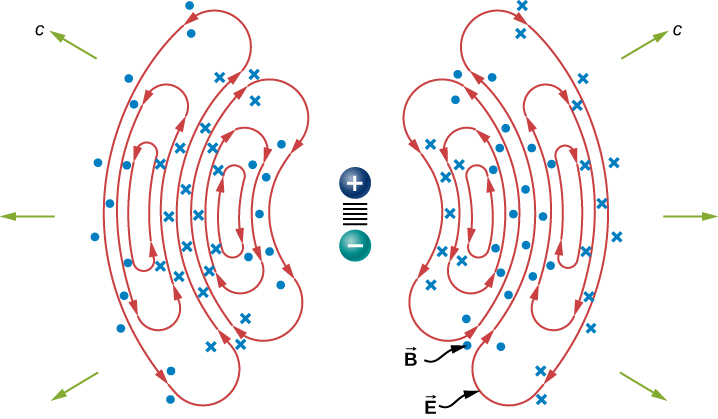
As linhas do campo elétrico em um plano são mostradas. O campo magnético é perpendicular a esse plano. Esse campo de radiação tem simetria cilíndrica em torno do eixo do dipolo. As linhas de campo próximas ao dipolo não são mostradas. O padrão não é nada uniforme em todas as direções. O sinal mais forte está em direções perpendiculares ao eixo da antena, que seria horizontal se a antena fosse montada verticalmente. Há intensidade zero ao longo do eixo da antena. Os campos detectados longe da antena são provenientes da mudança dos campos elétricos e magnéticos que se induzem mutuamente e viajam como ondas eletromagnéticas. Longe da antena, as frentes de onda, ou superfícies de igual fase para a onda eletromagnética, são quase esféricas. Ainda mais longe da antena, a radiação se propaga como ondas planas eletromagnéticas.
As ondas eletromagnéticas transportam energia para longe de sua fonte, semelhante a uma onda sonora transportando energia para longe de uma onda estacionária em uma corda de violão. Uma antena para receber sinais eletromagnéticos funciona ao contrário. As ondas eletromagnéticas de entrada induzem correntes oscilantes na antena, cada uma com sua própria frequência. O receptor de rádio inclui um circuito sintonizador, cuja frequência de ressonância pode ser ajustada. O sintonizador responde fortemente à frequência desejada, mas não a outras, permitindo que o usuário sintonize a transmissão desejada. Os componentes elétricos amplificam o sinal formado pelos elétrons em movimento. O sinal é então convertido em um formato de áudio e/ou vídeo.
Use essa simulação para transmitir ondas de rádio. Mexa o elétron do transmissor manualmente ou faça com que ele oscile automaticamente. Exiba o campo como uma curva ou vetores. O gráfico de faixas mostra as posições dos elétrons no transmissor e no receptor.


