12.2: A Lei Biot-Savart
- Page ID
- 184550
Ao final desta seção, você poderá:
- Explicar como derivar um campo magnético de uma corrente arbitrária em um segmento de linha
- Calcule o campo magnético a partir da lei de Biot-Savart em geometrias específicas, como uma corrente em uma linha e uma corrente em um arco circular
Vimos que a massa produz um campo gravitacional e também interage com esse campo. A carga produz um campo elétrico e também interage com esse campo. Como a carga móvel (ou seja, a corrente) interage com um campo magnético, podemos esperar que ela também crie esse campo — e o faz.
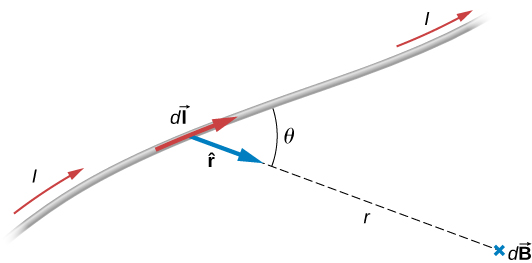
A equação usada para calcular o campo magnético produzido por uma corrente é conhecida como lei de Biot-Savart. É uma lei empírica nomeada em homenagem a dois cientistas que investigaram a interação entre um fio reto transportador de corrente e um ímã permanente. Essa lei nos permite calcular a magnitude e a direção do campo magnético produzido por uma corrente em um fio. A lei Biot-Savart afirma que em qualquer ponto\(P\) (Figura\(\PageIndex{1}\)), o campo magnético\(d\vec{B}\) devido a um elemento\(d\vec{l}\) de um fio transportador de corrente é dado por
\[d\vec{B} = \dfrac{\mu_0}{4 \pi} \dfrac{Id\vec{l} \times \hat{r}}{r^2}. \label{Biot-Savart law}\]
A constante\(\mu_0\) é conhecida como permeabilidade do espaço livre e é exatamente
\[\mu_0 = 4\pi \times 10^{-7}\, T \cdot m/A \label{eq1}\]
no sistema SI. O segmento de fio infinitesimal\(d\vec{l}\) está na mesma direção da corrente\(I\) (assumido positivo),\(r\) é a distância de\(d\vec{l}\) para\(P\) e\(\hat{r}\) é um vetor unitário que aponta de\(d\vec{l}\) para\(P\), conforme mostrado na Figura\(\PageIndex{1}\). A direção de\(d\vec{B}\) é determinada aplicando a regra da mão direita ao produto vetorial\(d\vec{l} \times \hat{r}\). A magnitude de\(d\vec{B}\) é
\[dB = \dfrac{\mu_0}{4\pi} \dfrac{I \, dl \, \sin \, \theta}{r^2} \label{eq2}\]
onde\(\theta\) está o ângulo entre\(d\vec{l}\)\(\hat{r}\) e. Observe que se\(\theta = 0\), então\(d\vec{B} = \vec{0}\). O campo produzido por um elemento atual não\(I d\vec{l}\) tem nenhum componente paralelo ao\(d\vec{l}\).
O campo magnético devido a um comprimento finito de fio transportador de corrente é encontrado integrando a Equação\ ref {eq1} ao longo do fio, nos dando a forma usual da lei de Biot-Savart.
O campo magnético\(\vec{B}\) devido a um elemento\(d\vec{l}\) de um fio transportador de corrente é dado por
\[\vec{B} = \dfrac{\mu_0}{4\pi} \int_{wire} \dfrac{I \, d\vec{l} \times \hat{r}}{r^2}. \label{BS}\]
Como essa é uma integral vetorial, contribuições de diferentes elementos atuais podem não apontar na mesma direção. Consequentemente, a integral geralmente é difícil de avaliar, mesmo para geometrias bastante simples. A estratégia a seguir pode ser útil.
Para resolver problemas da lei de Biot-Savart, as seguintes etapas são úteis:
- Identifique que a lei Biot-Savart é o método escolhido para resolver o problema dado. Se houver simetria na comparação do problema\(\vec{B}\) e\(d\vec{l}\), a lei de Ampère pode ser o método preferido para resolver a questão.
- Desenhe o comprimento do elemento atual\(d\vec{l}\) e o vetor unitário\(\hat{r}\) observando que\(d\vec{l}\) aponta na direção da corrente e\(\hat{r}\) aponta do elemento atual em direção ao ponto em que o campo é desejado.
- Calcule o produto cruzado\(d\vec{l} \times \hat{r}\). O vetor resultante fornece a direção do campo magnético de acordo com a lei de Biot-Savart.
- Use a Equação\ ref {BS} e substitua todas as quantidades dadas na expressão para resolver o campo magnético. Observe que todas as variáveis que permanecem constantes em todo o comprimento do fio podem ser consideradas fora da integração.
- Use a regra da direita para verificar a direção do campo magnético produzido a partir da corrente ou para anotar a direção do campo magnético se apenas a magnitude foi resolvida na parte anterior.
Um fio curto de 1,0 cm de comprimento carrega uma corrente de 2,0 A na direção vertical (Figura\(\PageIndex{2}\)). O resto do fio é blindado para não aumentar o campo magnético produzido pelo fio. Calcule o campo magnético no ponto P, que fica a 1 metro do fio na direção x.
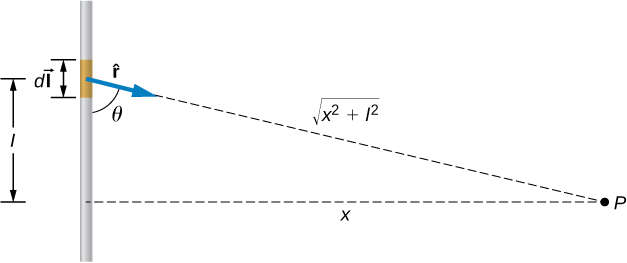
Estratégia
Podemos determinar o campo magnético em um ponto\(P\) usando a lei de Biot-Savart. Como o segmento atual é muito menor do que a distância x, podemos retirar a integral da expressão. A integração é convertida novamente em uma soma, mas apenas para pequenas\(dl\), como a qual agora escrevemos\(\Delta l\). Outra maneira de pensar sobre isso é que cada um dos valores do raio é quase o mesmo, não importa onde o elemento atual esteja no segmento da linha, se\(\Delta l\) for pequeno em comparação com x. O ângulo\(\theta\) é calculado usando uma função tangente. Usando os números dados, podemos calcular o campo magnético em\(P\).
Solução
O ângulo entre\(\Delta \vec{l}\) e\(\hat{r}\) é calculado a partir da trigonometria, conhecendo as distâncias l e x do problema:
\[\theta = \tan^{-1} \left(\dfrac{1 \, m}{0.01 \, m}\right) = 89.4^o. \nonumber\]
O campo magnético no ponto\(P\) é calculado pela lei de Biot-Savart (Equação\ ref {eq2}):
\[\begin{align*} B &= \dfrac{\mu_0}{4\pi}\dfrac{I \Delta l \, \sin \, \theta}{r^2} \\[4pt] &= (1 \times 10^{-7} T \cdot m/A)\left( \dfrac{2 \, A(0.01 \, m)\, sin \, (89.4^o)}{(1 \, m)^2}\right) \\[4pt] &= 2.0 \times 10^{-9}T. \end{align*}\]
A partir da regra da direita e da lei Biot-Savart, o campo é direcionado para a página.
Significância
Essa aproximação só é boa se o comprimento do segmento de linha for muito pequeno em comparação com a distância do elemento atual até o ponto. Caso contrário, a forma integral da lei de Biot-Savart deve ser usada em todo o segmento da linha para calcular o campo magnético.
Usando o exemplo\(\PageIndex{1}\), a que distância P teria que estar para medir a metade do campo magnético da resposta dada?
Solução
1,41 metros
Um fio carrega uma corrente I em um arco circular com raio R varrido por um ângulo arbitrário\(\theta\) (Figura\(\PageIndex{3}\)). Calcule o campo magnético no centro desse arco no ponto P.
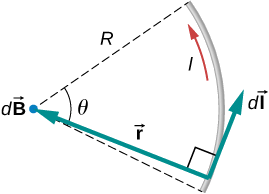
Estratégia
Podemos determinar o campo magnético no ponto P usando a lei de Biot-Savart. As direções radial e de comprimento do caminho estão sempre em um ângulo reto, então o produto transversal se transforma em multiplicação. Também sabemos que a distância ao longo do caminho dl está relacionada ao raio vezes o ângulo\(\theta\) (em radianos). Então, podemos retirar todas as constantes da integração e resolver o campo magnético.
Solução
A lei de Biot-Savart começa com a seguinte equação:
\[\vec{B} = \dfrac{\mu_0}{4\pi} \int_{wire} \dfrac{Id\vec{l} \times \hat{r}}{r^2}. \nonumber\]
À medida que nos integramos ao longo do arco, todas as contribuições para o campo magnético estão na mesma direção (fora da página), para que possamos trabalhar com a magnitude do campo. O produto cruzado se transforma em multiplicação porque o caminho\(dl\) e a direção radial são perpendiculares. Também podemos substituir a fórmula do comprimento do arco,\(dl = r\,d\theta\):
\[B = \dfrac{\mu_0}{4\pi} \int_{wire} \dfrac{Ir \, d\theta}{r^2}. \nonumber\]
A corrente e o raio podem ser retirados da integral porque são os mesmos, independentemente de onde estejamos no caminho. Isso deixa apenas a integral sobre o ângulo,
\[B = \dfrac{\mu_0I}{4\pi r} \int_{wire} d\theta.\nonumber\]
O ângulo varia no fio de 0 a\(\theta\); portanto, o resultado é
\[B = \dfrac{\mu_0I\theta}{4\pi r}. \nonumber\]
Significância
A direção do campo magnético no ponto\(P\) é determinada pela regra da direita, conforme mostrado no capítulo anterior. Se houver outros fios no diagrama junto com o arco e você for solicitado a encontrar o campo magnético líquido, encontre cada contribuição de um fio ou arco e adicione os resultados por superposição de vetores. Certifique-se de prestar atenção à direção de cada contribuição. Observe também que em uma situação simétrica, como um fio reto ou circular, as contribuições de lados opostos do ponto se\(P\) cancelam.
O laço de arame forma um círculo completo de raio R e corrente I. Qual é a magnitude do campo magnético no centro?
Solução
\(\dfrac{\mu_0 I}{2R}\)


