10.4: Regras de Kirchhoff
- Page ID
- 184519
Ao final da seção, você poderá:
- Regra estadual de junção de Kirchhoff
- Declare a regra do loop de Kirchhoff
- Analise circuitos complexos usando as regras de Kirchhoff
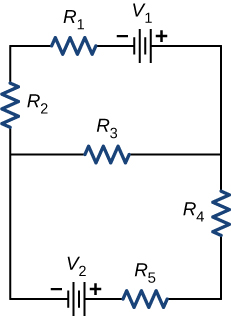
Acabamos de ver que alguns circuitos podem ser analisados reduzindo um circuito a uma única fonte de tensão e uma resistência equivalente. Muitos circuitos complexos não podem ser analisados com as técnicas em série paralelas desenvolvidas nas seções anteriores. Nesta seção, detalhamos o uso das regras de Kirchhoff para analisar circuitos mais complexos. Por exemplo, o circuito na Figura\(\PageIndex{1}\) é conhecido como circuito multi-loop, que consiste em junções. Uma junção, também conhecida como nó, é uma conexão de três ou mais fios. Nesse circuito, os métodos anteriores não podem ser usados, porque nem todos os resistores estão em séries claras ou configurações paralelas que podem ser reduzidas. Experimente. Os resistores\(R_1\)\(R_2\) estão em série e podem ser reduzidos a uma resistência equivalente. O mesmo se aplica aos resistores\(R_4\)\(R_5\) e. Mas o que você faz então?
Mesmo que esse circuito não possa ser analisado usando os métodos já aprendidos, duas regras de análise de circuito podem ser usadas para analisar qualquer circuito, simples ou complexo. As regras são conhecidas como regras de Kirchhoff, em homenagem ao inventor Gustav Kirchhoff (1824—1887).
- A primeira regra de Kirchhoff — a regra de junção. A soma de todas as correntes que entram em uma junção deve ser igual à soma de todas as correntes que saem da junção:\[\sum I_{in} = \sum I_{out}.\]
- A segunda regra de Kirchhoff — a regra do loop. A soma algébrica das mudanças de potencial em torno de qualquer caminho de circuito fechado (loop) deve ser zero:\[\sum V = 0.\]
Agora, fornecemos explicações sobre essas duas regras, seguidas por dicas de solução de problemas para aplicá-las e um exemplo prático que as usa.
Primeira regra de Kirchhoff
A primeira regra de Kirchhoff (a regra de junção) se aplica à carga que entra e sai de uma junção (Figura\(\PageIndex{2}\)). Conforme mencionado anteriormente, uma junção, ou nó, é uma conexão de três ou mais fios. A corrente é o fluxo de carga e a carga é conservada; portanto, qualquer carga que flua para a junção deve fluir para fora.
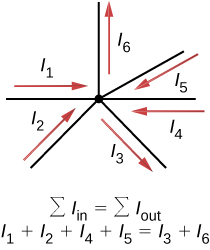
Embora seja uma simplificação excessiva, uma analogia pode ser feita com canos de água conectados em uma junção de encanamento. Se os fios da Figura\(\PageIndex{2}\) foram substituídos por canos de água e a água foi considerada incompressível, o volume de água que flui para a junção deve ser igual ao volume de água que sai da junção.
Segunda regra de Kirchhoff
A segunda regra de Kirchhoff (a regra do loop) se aplica a possíveis diferenças. A regra do loop é declarada em termos de potencial V em vez de energia potencial, mas os dois estão relacionados desde então\(U = qV\). Em um circuito fechado, qualquer que seja a energia fornecida por uma fonte de tensão, a energia deve ser transferida para outras formas pelos dispositivos do circuito, pois não há outras maneiras pelas quais a energia possa ser transferida para dentro ou para fora do circuito. A regra do loop de Kirchhoff afirma que a soma algébrica das diferenças de potencial, incluindo a tensão fornecida pelas fontes de tensão e pelos elementos resistivos, em qualquer loop deve ser igual a zero. Por exemplo, considere um loop simples sem junções, como na Figura\(\PageIndex{3}\).
O circuito consiste em uma fonte de tensão e três resistores de carga externos. Os rótulos a, b, c e d servem como referências e não têm outro significado. A utilidade desses rótulos se tornará aparente em breve. O circuito é designado como Loop abcda, e as etiquetas ajudam a acompanhar as diferenças de tensão à medida que percorremos o circuito. Comece no ponto a e vá até o ponto b. A tensão da fonte de tensão é adicionada à equação e a queda potencial do resistor\(R_1\) é subtraída. Do ponto b ao c, a queda potencial\(R_2\) é subtraída. De c a d, a queda potencial\(R_3\) é subtraída. Dos pontos d a a, nada é feito porque não há componentes.
A figura\(\PageIndex{4}\) mostra um gráfico da voltagem à medida que percorremos o circuito. A tensão aumenta à medida que cruzamos a bateria, enquanto a voltagem diminui à medida que viajamos por um resistor. A queda potencial, ou mudança no potencial elétrico, é igual à corrente através do resistor vezes a resistência do resistor. Como os fios têm uma resistência insignificante, a tensão permanece constante à medida que cruzamos os fios que conectam os componentes.
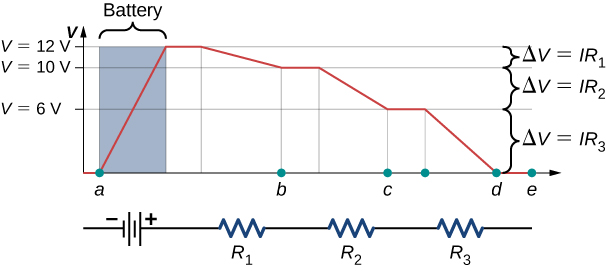
Então, a regra de loop de Kirchhoff afirma
\[V - IR_1 - IR_2 - IR_3 = 0.\]
A equação do loop pode ser usada para encontrar a corrente através do loop:
\[I = \frac{V}{R_1 +R_2 +R_3} = \frac{12.00 \, V}{1.00 \, \Omega + 2.00 \, \Omega + 3.00 \, \Omega} = 2.00 \, A.\]
Esse loop poderia ter sido analisado usando os métodos anteriores, mas demonstraremos o poder do método de Kirchhoff na próxima seção.
Aplicando as regras de Kirchhoff
Ao aplicar as regras de Kirchhoff, geramos um conjunto de equações lineares que nos permitem encontrar os valores desconhecidos nos circuitos. Podem ser correntes, tensões ou resistências. Cada vez que uma regra é aplicada, ela produz uma equação. Se houver tantas equações independentes quanto incógnitas, o problema poderá ser resolvido.
O uso do método de análise de Kirchhoff requer várias etapas, conforme listado no procedimento a seguir.
- Identifique pontos no diagrama de circuito usando letras minúsculas a, b, c,... Esses rótulos simplesmente ajudam na orientação.
- Localize as junções no circuito. As junções são pontos onde três ou mais fios se conectam. Identifique cada junção com as correntes e direções para dentro e para fora dela. Certifique-se de que pelo menos uma corrente aponte para dentro da junção e pelo menos um ponto de corrente para fora da junção.
- Escolha os loops no circuito. Cada componente deve estar contido em pelo menos um loop, mas um componente pode estar contido em mais de um loop.
- Aplique a regra de junção. Novamente, algumas junções não devem ser incluídas na análise. Você só precisa usar nós suficientes para incluir todas as correntes.
- Aplique a regra de loop. Use o mapa na Figura\(\PageIndex{5}\).
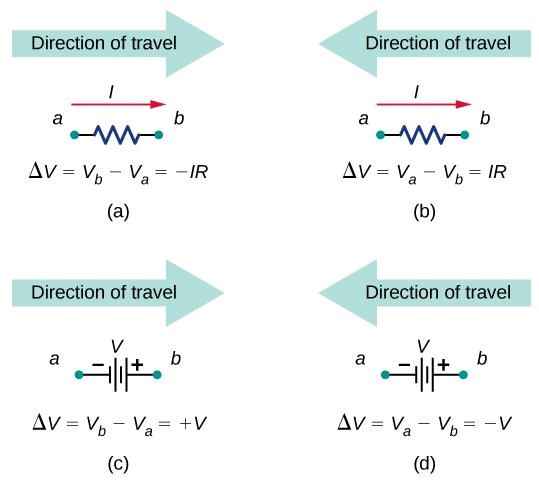
Vamos examinar algumas etapas desse procedimento mais de perto. Ao localizar as junções no circuito, não se preocupe com a direção das correntes. Se a direção do fluxo de corrente não for óbvia, escolher qualquer direção é suficiente, desde que pelo menos uma corrente aponte para a junção e pelo menos uma corrente aponte para fora da junção. Se a seta estiver na direção oposta ao fluxo de corrente convencional, o resultado da corrente em questão será negativo, mas a resposta ainda estará correta.
O número de nós depende do circuito. Cada corrente deve ser incluída em um nó e, portanto, incluída em pelo menos uma equação de junção. Não inclua nós que não sejam linearmente independentes, ou seja, nós que contêm as mesmas informações.
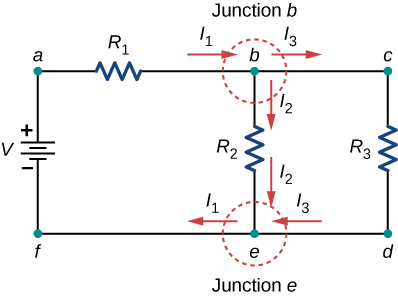
Considere a figura\(\PageIndex{6}\). Existem duas junções neste circuito: Junção b e Junção e. Os pontos a, c, d e f não são junções, porque uma junção deve ter três ou mais conexões. A equação para a junção b é\(I_1 = I_2 + I_3\), e a equação para a junção e é\(I_2 + I_3 = I_1\). Essas são equações equivalentes, então é necessário manter apenas uma delas.
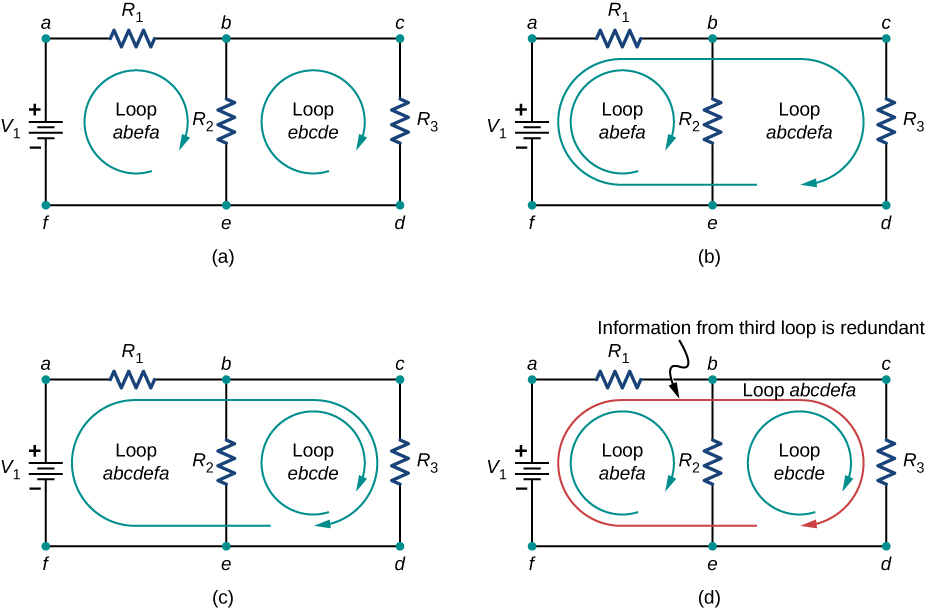
Ao escolher os loops no circuito, você precisa de loops suficientes para que cada componente seja coberto uma vez, sem repetir loops. \(\PageIndex{7}\)A figura mostra quatro opções de loops para resolver um circuito de amostra; as opções (a), (b) e (c) têm uma quantidade suficiente de loops para resolver o circuito completamente. A opção (d) reflete mais loops do que o necessário para resolver o circuito.
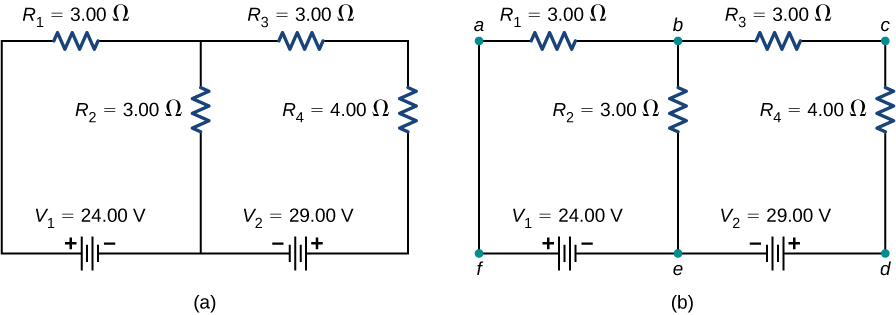
Considere o circuito na Figura\(\PageIndex{8a}\). Vamos analisar esse circuito para encontrar a corrente através de cada resistor. Primeiro, rotule o circuito conforme mostrado na parte (b).
Em seguida, determine as junções. Nesse circuito, cada um dos pontos b e e tem três fios conectados, tornando-os junções. Comece a aplicar a regra de junção de Kirchhoff\(\left(\sum I_{in} = \sum I_{out}\right)\) desenhando setas representando as correntes e rotulando cada seta, conforme mostrado na Figura\(\PageIndex{9}\). A junção b mostra isso\(I_1 = I_2 + I_3\) e a junção e mostra isso\(I_2 + I_3 = I_1\). Como a Junção e fornece as mesmas informações da Junção b, ela pode ser ignorada. Esse circuito tem três incógnitas, então precisamos de três equações linearmente independentes para analisá-lo.

Em seguida, precisamos escolher os loops. Na Figura\(\PageIndex{10}\), Loop abefa inclui a fonte de tensão\(V_1\)\(R_1\) e os resistores\(R_2\) e. O loop começa no ponto a, depois viaja pelos pontos b, e e f e depois volta ao ponto a. O segundo loop, Loop ebcde, começa no ponto e e inclui resistores\(R_2\) e\(R_3\) e a fonte de tensão\(V_2\).
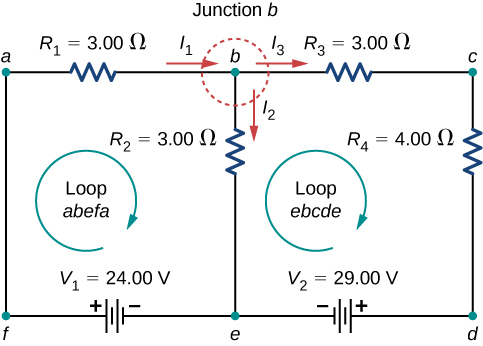
Agora podemos aplicar a regra de loop de Kirchhoff, usando o mapa na Figura\(\PageIndex{5}\). Começando no ponto a e indo para o ponto b, o resistor\(R_1\) é cruzado na mesma direção do fluxo de corrente\(I_1\), então a queda potencial\(I_1R_1\) é subtraída. Movendo-se do ponto b para o ponto e, o resistor\(R_2\) é cruzado na mesma direção do fluxo de corrente, de\(I_2\) modo que a queda potencial\(I_2R_2\) é subtraída. Movendo-se do ponto e para o ponto f, a fonte de tensão\(V_1\) é cruzada do terminal negativo para o terminal positivo, então\(V_1\) é adicionada. Não há componentes entre os pontos f e a. A soma das diferenças de tensão deve ser igual a zero:
\[Loop \, abefa: \, -I_1R_1 - I_2R_2 + V_1 = 0 \, or \, V_1 = I_1R_1 + I_2R_2.\]
Finalmente, verificamos o loop ebcde. Começamos no ponto e e passamos para o ponto b, cruzando\(R_2\) na direção oposta ao fluxo atual\(I_2\). A queda potencial\(I_2R_2\) é adicionada. Em seguida, cruzamos\(R_3\) e\(R_4\) na mesma direção do fluxo de corrente\(I_3\) e subtraímos as quedas potenciais\(I_3R_3\)\(I_3R_4\) e. Observe que a corrente é a mesma por meio de resistores\(R_3\) e\(R_4\), porque eles estão conectados em série. Finalmente, a fonte de tensão é cruzada do terminal positivo para o terminal negativo e a fonte de tensão\(V_2\) é subtraída. A soma dessas diferenças de tensão é igual a zero e produz a equação do loop
\[Loop \, ebcde: \, I_2R_2 - I_3(R_3 + R_4) - V_2 = 0.\]
Agora temos três equações, que podemos resolver para as três incógnitas.
\[\text{Junction b:} \, I_1 - I_2 - I_3 = 0. \label{eq1}\]
\[\text{Loop abefa:} \, I_1R_1 + I_2R_2 = V_1. \label{eq2}\]
\[\text{Loop ebcde:} \, I_2R_2 - I_3(R_3 + R_4) = V_2. \label{eq3}\]
Para resolver as três equações das três correntes desconhecidas, comece eliminando a corrente\(I_2\). Primeiro, adicione a Equação\ ref {eq1} vezes\(R_2\) à Equação\ ref {eq2}. O resultado é a Equação\ ref {eq4}:
\[(R_1 + R_2) I_1 - R_2I_3 = V_1.\]
\[6 \, \Omega I_1 - 3 \Omega I_3 = 24 \, V. \label{eq4}\]
Em seguida, subtraia a Equação\ ref {eq3} da Equação\ ref {eq2}. O resultado é a Equação\ ref {eq5}:
\[I_1R_1 + I_3(R_3 + R_4) = V_1 - V_2.\]
\[3 \Omega I_1 + 7 \Omega I_3 = -5 \, V. \label{eq5}\]
Podemos resolver as equações\ ref {eq4} e\ ref {eq5} para a corrente\(I_1\). Adicionar sete vezes Equation\ ref {eq4} e três vezes Equation\ ref {eq5} resulta em\(51 \, \Omega I_1 = 153 \, V\), ou\(I_1 = 3.00 \, A\). O uso da Equação\ ref {eq4} resulta em\(I_3 = -2.00 \, A\). Finalmente, a Equação\ ref {eq1} produz\(I_2 = I_1 - I_3 = 5.00 \, A\). Uma forma de verificar se as soluções são consistentes é verificar a energia fornecida pelas fontes de tensão e a energia dissipada pelos resistores:
\[P_{in} = I_1V_1 + I_3V_2 = 130 \, W, \nonumber\]
\[P_{out} = I_1^2R_1 + I_2^2R_2 + I_3^2R_3 + I_3^2R_4 = 130 \, W. \nonumber\]
Observe que a solução para a corrente\(I_3\) é negativa. Essa é a resposta correta, mas sugere que a seta originalmente desenhada na análise de junção é a direção oposta ao fluxo de corrente convencional. A energia fornecida pela segunda fonte de tensão é 58 W e não −58 W.
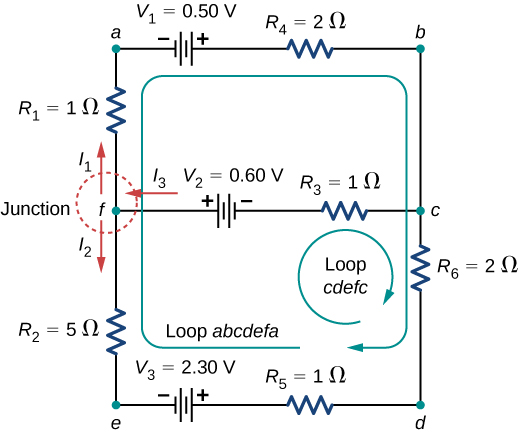
Encontre as correntes que fluem no circuito na Figura\(\PageIndex{11}\).
Estratégia
Esse circuito é suficientemente complexo para que as correntes não possam ser encontradas usando a lei de Ohm e as técnicas de séries paralelas — é necessário usar as regras de Kirchhoff. As correntes foram rotuladas e\(I_1, \, I_2\),\(I_3\) na figura, foram feitas suposições sobre suas direções. Os locais no diagrama foram rotulados com as letras de a a h. Na solução, aplicamos as regras de junção e loop, buscando três equações independentes para nos permitir resolver as três correntes desconhecidas.
Solução
A aplicação das regras de junção e loop produz as três equações a seguir. Temos três incógnitas, então três equações são necessárias.
\[Junction \, c: \, I_1 + I_2 = I_3.\]
\[Loop \, abcdefa: \, I_1(R_1 + R_4) - I_2(R_2 + R_5 + R_6) = V_1 - V_3.\]
\[Loop \, cdefc: \, I_2(R_2 + R_5 + R_6) + I_3R_3 = V_2 + V_3.\]
Simplifique as equações colocando as incógnitas em um lado das equações.
\[Junction \, c: \, I_1 + I_2 - I_3 = 0.\]
\[Loop \, abcdefa: \, I_1 (3 \Omega) - I_2(8 \Omega) = 0.5 \, V - 2.30 \, V.\]
\[Loop \, cdefc: \, I_2 (8 \Omega) + I_3 (1 \Omega) = 0.6 \, V + 2.30 \, V.\]
Simplifique as equações. A primeira equação do loop pode ser simplificada dividindo os dois lados por 3,00. A segunda equação do loop pode ser simplificada dividindo os dois lados por 6,00.
\[Junction \, c: \, I_1 + I_2 - I_3 = 0.\]
\[Loop \, abcdefa: \, I_1 (3 \Omega) - I_2(8 \Omega) = - 1.8 \, V.\]
\[Loop \, cdefc: \, I_2 (8 \Omega) + I_3 (1 \Omega) = 2.90 \, V.\]
Os resultados são
\[I_1 = 0.20 \, A, \, I_2 = 0.30 \, A, \, I_3 = 0.50 \, A.\]
Significância
Um método para verificar os cálculos é calcular a energia dissipada pelos resistores e a energia fornecida pelas fontes de tensão:
\[P_{R_1} = I_1^2R_1 = 0.04 \, W.\]
\[P_{R_2} = I_2^2R_2 = 0.45 \, W.\]
\[P_{R_3} = I_3^2R_3 = 0.25 \, W.\]
\[P_{R_4} = I_1^2R_4 = 0.08 \, W.\]
\[P_{R_5} = I_2^2R_5 = 0.09 \, W.\]
\[P_{R_6} = I_2^2R_1 = 0.18 \, W.\]
\[P_{dissipated} = 1.09 \, W.\]
\[P_{source} = I_1V_1 + I_2V_3 + I_3V_2 = 0.10 \, + 0.69 \, W + 0.30 \, W = 1.09 \, W.\]
A energia fornecida é igual à energia dissipada pelos resistores.
Ao considerar o esquema a seguir e a energia fornecida e consumida por um circuito, uma fonte de tensão sempre fornecerá energia ao circuito ou uma fonte de tensão pode consumir energia?
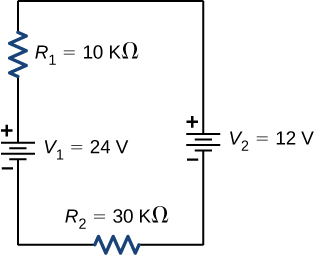
- Responda
-
O circuito pode ser analisado usando a regra de loop de Kirchhoff. A primeira fonte de tensão fornece energia:
Contributors and Attributions


