2.4: Capacidade térmica e equipartição de energia

Objetivos de

Ao final desta seção, você poderá:

• Resolva problemas envolvendo transferência de calor de e para gases monoatômicos ideais cujos volumes são mantidos constantes
• Resolva problemas semelhantes para gases ideais não monoatômicos com base no número de graus de liberdade de uma molécula
• Estime as capacidades térmicas dos metais usando um modelo baseado em graus de liberdade

No capítulo sobre temperatura e calor, definimos a capacidade térmica específica com a equação\(Q = mc\Delta T\), ou\(c = (1/m)Q/\Delta T\). No entanto, as propriedades de um gás ideal dependem diretamente do número de moles em uma amostra, então aqui definimos a capacidade térmica específica em termos do número de moles, não da massa. Além disso, quando falamos sobre sólidos e líquidos, ignoramos qualquer alteração no volume e na pressão com as mudanças na temperatura — uma boa aproximação para sólidos e líquidos, mas para gases, precisamos estabelecer algumas condições nas mudanças de volume ou pressão. Aqui, nos concentramos na capacidade de aquecimento com o volume mantido constante. Podemos calculá-lo para um gás ideal.

Capacidade térmica de um gás monoatômico ideal em volume constante

Definimos a capacidade de calor molar em volume constante \(C_V\)como

\[\underbrace{C_V = \dfrac{1}{n} \dfrac{Q}{\Delta T}}_{\text{with constant V}}\nonumber \]

Isso geralmente é expresso no formulário

\[Q = nC_V\Delta T\nonumber \]

Se o volume não mudar, não há deslocamento geral, portanto, nenhum trabalho é feito e a única mudança na energia interna é devido ao fluxo de calor\(\Delta E_{int} = Q\). (Essa declaração será discutida mais adiante no próximo capítulo.) Usamos a equação\(E_{int} = 3nRT/2\) para escrever\(\Delta E_{int} = 3nR\Delta T/2\) e substituir\(\Delta E\) por Q para encontrar\(Q = 3nR\Delta T/2\), o que fornece o seguinte resultado simples para um gás monoatômico ideal:

\[C_V = \dfrac{3}{2}R.\nonumber \]

É independente da temperatura, o que justifica nosso uso de diferenças finitas em vez de uma derivada. Essa fórmula concorda bem com os resultados experimentais.

No próximo capítulo, discutimos o calor específico do molar em pressão constante\(C_p\), que é sempre maior que\(C_V\).

Exemplo\(\PageIndex{1}\): Calculating Temperature

Uma amostra de 0,125 kg de xenônio está contida em um cilindro rígido de metal, grande o suficiente para que o xenônio possa ser modelado como um gás ideal, a uma temperatura de\(20.0^oC\). O cilindro é movido para fora em um dia quente de verão. À medida que o xenônio entra em equilíbrio ao atingir a temperatura ambiente, 180 J de calor são conduzidos para ele através das paredes do cilindro. Qual é a temperatura de equilíbrio? Ignore a expansão do cilindro de metal.

Solução

1. Identifique os conhecidos: Sabemos que a temperatura inicial\(T_1\) é\(20.0^oC\), o calor Q é 180 J e a massa m do xenônio é 0,125 kg.
2. Identifique o desconhecido. Precisamos da temperatura final, então precisaremos\(\Delta T\).
3. Determine quais equações são necessárias. Como o gás xenônio é monoatômico, podemos usar\(Q = 3nR\Delta T/2\). Então precisamos do número de toupeiras\(n = m/M\).
4. Substitua os valores conhecidos nas equações e resolva as incógnitas.

A massa molar do xenônio é 131,3 g, então obtemos

\[n = \dfrac{125 \, g}{131.3 \, g/mol} = 0.952 \, mol, \nonumber\nonumber \]

\[\Delta T = \dfrac{2Q}{3nR} = \dfrac{2(180 \, J)}{3(0.952 \, mol)(8.31 \, J/mol \cdot \, ^oC)} = 15.2^oC. \nonumber\nonumber \]

Portanto, a temperatura final é\(35.2^oC \). O problema também poderia ser resolvido em kelvin; como um kelvin tem o mesmo tamanho de um grau Celsius de mudança de temperatura, você obteria\(\Delta T = 15.2 \, K \).

Significância

O aquecimento de um gás ideal ou quase ideal em volume constante é importante nos motores dos automóveis e em muitos outros sistemas práticos.

Exercício\(\PageIndex{1}\)

Suponha que 2 moles de gás hélio a 200 K sejam misturados com 2 moles de gás criptônio a 400 K em um calorímetro. Qual é a temperatura final?

Resposta

Como o número de moles é igual e sabemos que as capacidades de calor molar dos dois gases são iguais, a temperatura está a meio caminho entre as temperaturas iniciais, 300 K.

Gostaríamos de generalizar nossos resultados para gases ideais com mais de um átomo por molécula. Em tais sistemas, as moléculas podem ter outras formas de energia além da energia cinética translacional, como energia cinética rotacional e energias cinéticas e potenciais vibracionais. Veremos que uma regra simples nos permite determinar as energias médias presentes nessas formas e resolver problemas da mesma forma que fazemos com os gases monoatômicos.

Graus de liberdade

Na seção anterior, descobrimos isso\(\frac{1}{2}mv^2 = \frac{3}{2}k_BT\) e\(v^2 = 3v_x^2\), daí resulta\(\frac{1}{2}mv_x^2 = \frac{1}{2}k_BT\). A mesma equação é válida\(\frac{3}{2}k_BT\) como a soma das contribuições\(\frac{1}{2}k_BT\) de cada uma das três dimensões do movimento translacional. Mudando para o gás como um todo, vemos que o 3 na fórmula\(C_V = \frac{3}{2}R\) também reflete essas três dimensões. Definimos um grau de liberdade como um possível movimento independente de uma molécula, como cada uma das três dimensões da tradução. Então, deixando d representar o número de graus de liberdade, a capacidade térmica molar em volume constante de um gás monoatômico ideal é\(C_V = \frac{d}{2}R\), onde\(d = 3\).

O ramo da física chamado mecânica estatística nos diz, e o experimento confirma, que\(C_V\) qualquer gás ideal é dado por essa equação, independentemente do número de graus de liberdade. Esse fato decorre de um resultado mais geral, o teorema da equipartição, que é válido na termodinâmica clássica (não quântica) para sistemas em equilíbrio térmico sob condições técnicas que estão além do nosso escopo. Aqui, mencionamos apenas que, em um sistema, a energia é compartilhada entre os graus de liberdade por meio de colisões.

Teorema da equipartição

A energia de um sistema termodinâmico em equilíbrio é dividida igualmente entre seus graus de liberdade. Assim, a capacidade térmica molar de um gás ideal é proporcional ao seu número de graus de liberdade, d:\[C_V = \dfrac{d}{2}R.\nonumber \]

Esse resultado se deve ao físico escocês James Clerk Maxwell (1831 a 1871), cujo nome aparecerá várias vezes neste livro.

Por exemplo, considere um gás diatômico ideal (um bom modelo para nitrogênio e oxigênio\(O_2\)).\(N_2\) Esse gás tem mais graus de liberdade do que um gás monoatômico. Além dos três graus de liberdade de translação, ele tem dois graus de liberdade de rotação perpendiculares ao seu eixo. Além disso, a molécula pode vibrar ao longo de seu eixo. Esse movimento geralmente é modelado pela imaginação de uma mola conectando os dois átomos, e sabemos pelo movimento harmônico simples que esse movimento tem energia cinética e potencial. Cada uma dessas formas de energia corresponde a um grau de liberdade, dando mais duas.

Poderíamos esperar que, para um gás diatômico, usássemos 7 como o número de graus de liberdade; classicamente, se as moléculas de um gás tivessem apenas energia cinética translacional, as colisões entre as moléculas logo as fariam girar e vibrar. No entanto, conforme explicado no módulo anterior, a mecânica quântica controla quais graus de liberdade estão ativos. O resultado é mostrado na Figura\(\PageIndex{1}\). Tanto as energias rotacionais quanto as vibracionais são limitadas a valores discretos. Para temperaturas abaixo de cerca de 60 K, as energias das moléculas de hidrogênio são muito baixas para que uma colisão leve o estado rotacional ou vibracional de uma molécula da energia mais baixa para a segunda mais baixa, então a única forma de energia é a energia cinética translacional, e\(d = 3\) ou\(C_V = 3R/2\) como em um gás monoatômico. Acima dessa temperatura, os dois graus de liberdade de rotação começam a contribuir, ou seja, algumas moléculas são excitadas para o estado rotacional com a segunda menor energia. (Essa temperatura é muito menor do que aquela em que as rotações dos gases monoatômicos contribuem, porque as moléculas diatômicas têm inércias rotacionais muito maiores e, portanto, energias rotacionais muito menores.) De aproximadamente a temperatura ambiente (um pouco menos de 300 K) a cerca de 600 K, os graus de liberdade de rotação estão totalmente ativos, mas os vibracionais não estão,\(d = 5\) e. Então, finalmente, acima de cerca de 3000 K, os graus de liberdade vibracional estão totalmente ativos, e\(d = 7\) como a teoria clássica previu.

Figura\(\PageIndex{1}\): A capacidade térmica molar do hidrogênio em função da temperatura (em uma escala logarítmica). Os três “degraus” ou “platôs” mostram números diferentes de graus de liberdade que as energias típicas das moléculas devem alcançar para serem ativadas. A energia cinética translacional corresponde a três graus de liberdade, rotacional a outros dois e vibracional a mais dois.

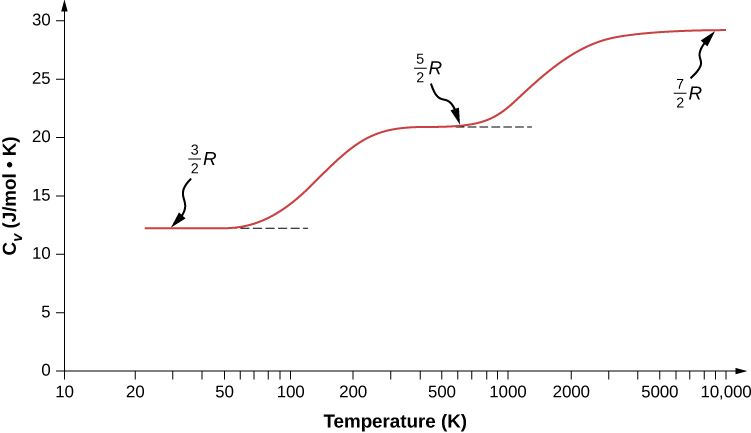
As moléculas poliatômicas normalmente têm um grau adicional de liberdade rotacional à temperatura ambiente, pois têm momentos de inércia comparáveis em torno de qualquer eixo. Assim, em temperatura ambiente, eles têm\(d = 6\) e em alta temperatura,\(d = 8\). Normalmente assumimos que os gases têm os valores teóricos da temperatura ambiente de d.

Conforme mostrado na Tabela\(\PageIndex{1}\), os resultados concordam bem com os experimentos de muitos gases monoatômicos e diatômicos, mas o acordo para gases triatômicos é justo. As diferenças surgem das interações que ignoramos entre e dentro das moléculas.

Tabela\(\PageIndex{1}\):\(C_V/R\) para vários gases monoatômicos, diatômicos e triatômicos

Gás	\(C_V/R\)em 1 caixa eletrônico\(25^oC\) e 1 caixa eletrônico
Ar	\ (C_V/R\) em\(25^oC\) e 1 atm">1,50
Ele	\ (C_V/R\) em\(25^oC\) e 1 atm">1,50
Ne	\ (C_V/R\) em\(25^oC\) e 1 atm">1,50
CO	\ (C_V/R\) em\(25^oC\) e 1 atm">2,50
\(H_2\)	\ (C_V/R\) em\(25^oC\) e 1 atm">2,47
\(N_2\)	\ (C_V/R\) em\(25^oC\) e 1 atm">2,50
\(O_2\)	\ (C_V/R\) em\(25^oC\) e 1 atm">2,53
\(F_2\)	\ (C_V/R\) em\(25^oC\) e 1 atm">2.8
\(CO_2\)	\ (C_V/R\) em\(25^oC\) e 1 atm">3,48
\(H_2S\)	\ (C_V/R\) em\(25^oC\) e 1 atm">3,13
\(N_2O\)	\ (C_V/R\) em\(25^oC\) e 1 atm">3,66

E quanto à energia interna para gases diatômicos e poliatômicos? Para esses gases,\(C_V\) é uma função da temperatura (Figura\(\PageIndex{1}\)), então não temos o tipo de resultado simples que temos para gases monoatômicos ideais.

Capacidade térmica molar de elementos sólidos

A ideia de equipartição leva a uma estimativa da capacidade térmica molar de elementos sólidos em temperaturas normais. Podemos modelar os átomos de um sólido anexados aos átomos vizinhos por molas (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Em um modelo simples de um elemento sólido, cada átomo é ligado a outros por seis molas, duas para cada movimento possível: x, y e z. Cada um dos três movimentos corresponde a dois graus de liberdade, um para energia cinética e outro para energia potencial. Assim\(d = 6\).

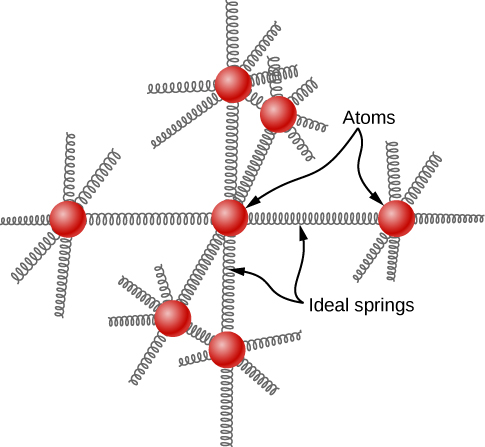
Analogamente à discussão sobre vibração no módulo anterior, cada átomo tem seis graus de liberdade: uma cinética e um potencial para cada uma das direções x -, y - e z. Consequentemente, o calor molar específico de um metal deve ser de 3 R. Esse resultado, conhecido como Lei de Dulong e Petit, funciona muito bem experimentalmente em temperatura ambiente. (Para cada elemento, ele falha em baixas temperaturas por motivos de mecânica quântica. Como os efeitos quânticos são particularmente importantes para partículas de baixa massa, a Lei de Dulong e Petit já falha em temperatura ambiente para alguns elementos leves, como berílio e carbono. Ele também falha em alguns elementos mais pesados por vários motivos além do que podemos abordar.)

Estratégia de resolução de problemas: capacidade térmica e equipartição

A estratégia para resolver esses problemas é a mesma das Mudanças de Fase para os efeitos da transferência de calor. A única novidade é que você deve determinar se o caso que acabou de ser apresentado — gases ideais em volume constante — se aplica ao problema. (Para elementos sólidos, pesquisar a capacidade térmica específica é geralmente melhor do que estimá-la a partir da Lei de Dulong e Petit.) No caso de um gás ideal, determine o número d de graus de liberdade do número de átomos na molécula de gás e use-o para calcular\(C_V\) (ou use\(C_V\) para resolver d).

Exemplo\(\PageIndex{2}\): Calculating Temperature: Calorimetry with an Ideal Gas

Um pedaço de 300 g de gálio sólido (um metal usado em dispositivos semicondutores) em seu ponto de fusão de apenas\(30.0^oC\) está em contato com 12,0 moles de ar (presumivelmente diatômico)\(95.0^oC\) em um recipiente isolado. Quando o ar atinge o equilíbrio com o gálio, 202 g do gálio derretem. Com base nesses dados, qual é o calor da fusão do gálio? Suponha que o volume do ar não mude e não haja outras transferências de calor.

Estratégia

Usaremos a equação\(Q_{hot} + Q_{cold} = 0\). Como parte do gálio não derrete, sabemos que a temperatura final ainda é o ponto de fusão. Então, o único\(Q_{hot}\) é o calor perdido à medida que o ar esfria,\(Q_{hot} = n_{air}C_V\Delta T\), onde\(C_V = 5R/2\). O único\(Q_{cold}\) é o calor latente de fusão do gálio,\(Q_{cold} = m_{Ga}L_f\). É positivo porque o calor flui para o gálio.

Solução

1. Configure a equação:\[n_{air}C_V\Delta T + m_{Ga}L_f = 0.\nonumber \]
2. Substitua os valores conhecidos e resolva:\[(12.0 \, mol) \left(\dfrac{5}{2}\right) \left(8.31 \dfrac{J}{mol \cdot \, ^oC}\right)(30.0^oC - 95.0^oC) + (0.202 \, kg)L_f = 0.\nonumber \]

Resolvemos descobrir que o calor de fusão do gálio é de 80,2 kJ/kg.