2.2: Modelo molecular de um gás ideal

Objetivos de

Ao final desta seção, você poderá:

• Aplique a lei do gás ideal em situações que envolvam a pressão, o volume, a temperatura e o número de moléculas de um gás
• Use a unidade de moles em relação ao número de moléculas e massas moleculares e macroscópicas
• Explique a lei do gás ideal em termos de moles em vez de números de moléculas
• Aplique a lei do gás van der Waals a situações em que a lei do gás ideal é inadequada

Nesta seção, exploramos o comportamento térmico dos gases. Nossa palavra “gás” vem da palavra flamenga que significa “caos”, usada pela primeira vez para vapores pelo químico do século XVII J. B. van Helmont. O termo era mais apropriado do que ele imaginava, porque os gases consistem em moléculas se movendo e colidindo aleatoriamente umas com as outras. Essa aleatoriedade torna a conexão entre os domínios microscópico e macroscópico mais simples para gases do que para líquidos ou sólidos.

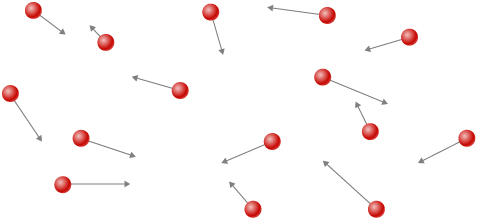
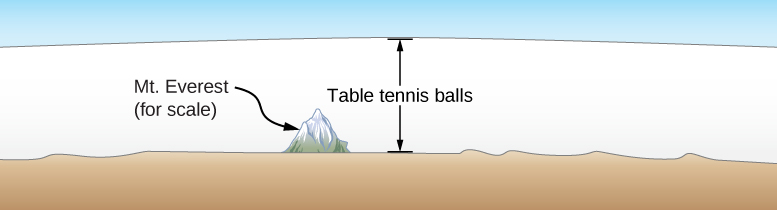
Como os gases diferem dos sólidos e líquidos? Em condições normais, como as do ar ao nosso redor, a diferença é que as moléculas dos gases estão muito mais afastadas do que as dos sólidos e líquidos. Como as distâncias típicas entre as moléculas são grandes em comparação com o tamanho de uma molécula, conforme ilustrado na Figura\(\PageIndex{1}\), as forças entre elas são consideradas insignificantes, exceto quando elas entram em contato umas com as outras durante colisões. Além disso, em temperaturas bem acima da temperatura de ebulição, o movimento das moléculas é rápido e os gases se expandem rapidamente para ocupar todo o volume acessível. Em contraste, em líquidos e sólidos, as moléculas estão mais próximas, e o comportamento das moléculas em líquidos e sólidos é altamente limitado pelas interações das moléculas umas com as outras. As propriedades macroscópicas de tais substâncias dependem fortemente das forças entre as moléculas e, como muitas moléculas estão interagindo, os “problemas de muitos corpos” resultantes podem ser extremamente complicados (consulte a seção sobre Física da Matéria Condensada).

Figura\(\PageIndex{1}\): Átomos e moléculas em um gás são normalmente amplamente separados. Como as forças entre eles são bastante fracas nessas distâncias, as propriedades de um gás dependem mais do número de átomos por unidade de volume e da temperatura do que do tipo de átomo.

As leis do gás

No capítulo anterior, vimos uma consequência do grande espaçamento intermolecular dos gases: os gases são facilmente comprimidos. A Tabela 1.4.1 mostra que os gases têm coeficientes de expansão de volume maiores do que os sólidos ou líquidos. Esses grandes coeficientes significam que os gases se expandem e se contraem muito rapidamente com as mudanças de temperatura. Também vimos (na seção sobre expansão térmica) que a maioria dos gases se expande na mesma taxa ou tem o mesmo coeficiente de expansão de volume,\(\beta\). Isso levanta uma questão: Por que todos os gases agem quase da mesma maneira, quando todos os vários líquidos e sólidos têm taxas de expansão amplamente variadas?

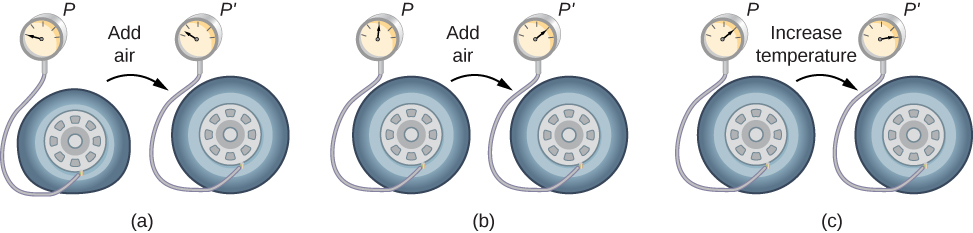
Para estudar como a pressão, a temperatura e o volume de um gás se relacionam entre si, considere o que acontece quando você bombeia ar para um pneu de carro vazio. O volume do pneu aumenta primeiro em proporção direta à quantidade de ar injetada, sem muito aumento na pressão do pneu. Depois que o pneu se expande para quase todo o tamanho, as paredes do pneu limitam sua expansão de volume. Se continuarmos bombeando ar para o pneu, a pressão aumenta. Quando o carro é conduzido e os pneus flexionam, a temperatura aumenta e, portanto, a pressão aumenta ainda mais (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Quando o ar é bombeado para um pneu vazio, seu volume primeiro aumenta sem muito aumento na pressão. (b) Quando o pneu está cheio até certo ponto, as paredes do pneu resistem a uma maior expansão e a pressão aumenta com mais ar. (c) Uma vez que o pneu é inflado, sua pressão aumenta com a temperatura.

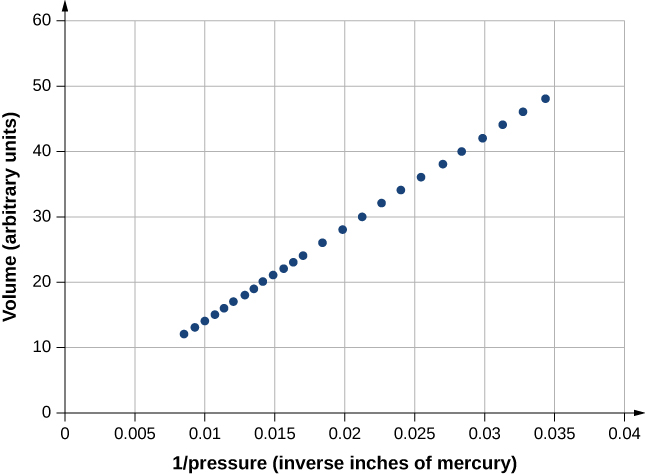
A figura\(\PageIndex{3}\) mostra dados dos experimentos de Robert Boyle (1627—1691), ilustrando o que hoje é chamado de lei de Boyle: Em temperatura e número de moléculas constantes, a pressão absoluta de um gás e seu volume são inversamente proporcionais. (Lembre-se da seção sobre Mecânica dos Fluidos que a pressão absoluta é a pressão real e a pressão manométrica é a pressão absoluta menos a pressão ambiente, normalmente a pressão atmosférica.) O gráfico na Figura\(\PageIndex{3}\) mostra essa relação como uma proporcionalidade inversa do volume à pressão.

Figura\(\PageIndex{3}\): Robert Boyle e seu assistente descobriram que o volume e a pressão são inversamente proporcionais. Aqui, seus dados são plotados como V versus 1/p; a linearidade do gráfico mostra a proporcionalidade inversa. O número mostrado como volume é, na verdade, a altura em polegadas de ar em um tubo de vidro cilíndrico. O volume real era aquela altura multiplicada pela área da seção transversal do tubo, que Boyle não publicou. Os dados são do livro de Boyle A Defense of the Doctrine Touching the Spring and Weight of the Air..., p. 60.

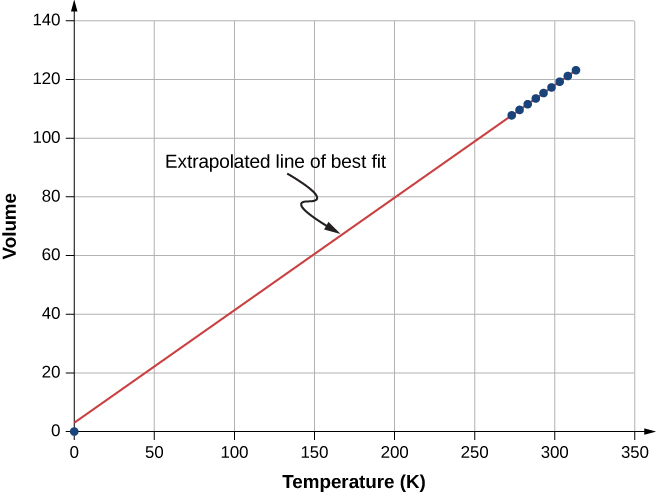
\(\PageIndex{4}\)A figura mostra dados experimentais que ilustram o que é chamado de lei de Charles, em homenagem a Jacques Charles (1746—1823). A lei de Charles afirma que, com pressão e número de moléculas constantes, o volume de um gás é proporcional à sua temperatura absoluta.

Figura\(\PageIndex{4}\): Dados experimentais que mostram que, em pressão constante, o volume é aproximadamente proporcional à temperatura. A linha mais adequada passa aproximadamente pela origem. ²

Semelhante é a lei de Amonton ou de Gay-Lussac, que afirma que em volume e número constantes de moléculas, a pressão é proporcional à temperatura. Essa lei é a base do termômetro de gás de volume constante, discutido no capítulo anterior. (As histórias dessas leis e o crédito apropriado para elas são mais complicadas do que podem ser discutidas aqui.)

Sabe-se experimentalmente que para gases de baixa densidade (de forma que suas moléculas ocupem uma fração insignificante do volume total) e em temperaturas bem acima do ponto de ebulição, essas proporcionalidades mantêm uma boa aproximação. Não é de surpreender que, com as outras quantidades mantidas constantes, a pressão ou o volume sejam proporcionais ao número de moléculas. Mais surpreendentemente, quando as proporcionalidades são combinadas em uma única equação, a constante de proporcionalidade é independente da composição do gás. A equação resultante para todos os gases se aplica no limite de baixa densidade e alta temperatura; é a mesma para oxigênio e para hexafluoreto de hélio ou urânio. Um gás nesse limite é chamado de gás ideal; ele obedece à lei do gás ideal, que também é chamada de equação de estado de um gás ideal.

Lei do Gás Ideal

A lei do gás ideal afirma que\[pV = Nk_BT,\] onde p é a pressão absoluta de um gás, V é o volume que ele ocupa, N é o número de moléculas no gás e T é sua temperatura absoluta.

A constante\(k_B\) é chamada de constante de Boltzmann em homenagem ao físico austríaco Ludwig Boltzmann (1844-1906) e tem o valor

\[k_B = 1.38 \times 10^{-23} \, J/K.\]

A lei do gás ideal descreve o comportamento de qualquer gás real quando sua densidade é baixa o suficiente ou sua temperatura alta o suficiente para que esteja longe da liquefação. Isso engloba muitas situações práticas. Na próxima seção, veremos por que é independente do tipo de gás.

Em muitas situações, a lei do gás ideal é aplicada a uma amostra de gás com um número constante de moléculas; por exemplo, o gás pode estar em um recipiente selado. Se N for constante, a resolução de N mostra que pV/T é constante. Podemos escrever esse fato de uma forma conveniente:

\[\dfrac{p_1V_1}{T_1} = \dfrac{p_2V_2}{T_2},\]

onde os subscritos 1 e 2 se referem a quaisquer dois estados do gás em momentos diferentes. Novamente, a temperatura deve ser expressa em kelvin e a pressão deve ser a pressão absoluta, que é a soma da pressão manométrica e da pressão atmosférica.

Exemplo\(\PageIndex{1}\): Calculating Pressure Changes Due to Temperature Changes

Suponha que o pneu da bicicleta esteja totalmente inflado, com uma pressão absoluta de\(7.00 \times 10^5 \, Pa\) (uma pressão manométrica de pouco menos\(90.0 \, lb/in^2\)) a uma temperatura de\(18.0^oC\). Qual é a pressão após o aumento da temperatura\(35.0^oC\) em um dia quente? Suponha que não haja vazamentos ou mudanças significativas no volume.

Estratégia

A pressão no pneu está mudando apenas por causa das mudanças de temperatura. Conhecemos a pressão inicial\(p_0 = 7.00 \times 10^5 \, Pa\), a temperatura\(T_0 = 18.0^oC\) inicial e a temperatura final\(T_f = 35.0^oC\). Devemos encontrar a pressão final\(p_f\). Como o número de moléculas é constante, podemos usar a equação

\[\dfrac{p_fV_f}{T_f} = \dfrac{p_0V_0}{T_0}.\]

Como o volume é constante,\(V_f\)\(V_0\) é o mesmo e eles se dividem. Portanto,

\[\dfrac{p_f}{T_f} = \dfrac{p_0}{T_0}.\]

Em seguida, podemos reorganizar isso para resolver\(p_f\):

\[p_f = p_0 \dfrac{T_f}{T_0},\]

onde a temperatura deve estar em Kelvin.

Solução

1. Converta temperaturas de graus Celsius em kelvin\[T_0 = (18.0 + 273)K = 291 \, K,\]\[T_f = (35.0 + 273)K = 308 \, K.\]
2. Substitua os valores conhecidos na equação,\[p_f = p_0\dfrac{T_f}{T_0} = 7.00 \times 10^5 \, Pa \left(\dfrac{308 \, K}{291 \, K}\right) = 7.41 \times 10^5 \, Pa.\]

Significância

A temperatura final é aproximadamente\(6\%\) maior que a temperatura original, então a pressão final também é quase\(6\%\) maior. Observe que a pressão absoluta (consulte Mecânica dos Fluidos) e a temperatura absoluta (consulte Temperatura e Calor) devem ser usadas na lei do gás ideal.

Exemplo\(\PageIndex{2}\): Calculating the Number of Molecules in a Cubic Meter of Gas

Quantas moléculas existem em um objeto típico, como gás em um pneu ou água em um copo? Esse cálculo pode nos dar uma ideia de quão grande N normalmente é. Vamos calcular o número de moléculas no ar que um jovem adulto saudável inala em uma respiração, com um volume de 500 mL, na temperatura e pressão padrão (STP), que é definida como\(0^oC\) pressão atmosférica. (Aparentemente, nosso jovem adulto está ao ar livre no inverno.)

Estratégia

Como a pressão, o volume e a temperatura estão todos especificados, podemos usar a lei do gás ideal,\ (pV = K_Bt\}, para encontrar N.

Solução

1. Identifique os conhecidos. \[T = 0^oC = 273 \, K, \, p = 1.01 \times 10^5 \, Pa, \, V = 500 \, mL = 5 \times 10^{-4} \, m^3, \, k_B = 1.38 \times 10^{-23} \, J/K\]
2. Substitua os valores conhecidos na equação e resolva por N. \[N = \dfrac{pV}{k_BT} = \dfrac{(1.01 \times 10^5 \, Pa)(5 \times 10^{-4} \, m^3)}{(1.38 \times 10^{-23} \, J/K)(273 \, K)} = 1.34 \times 10^{22} \, molecules\]

O significado N é enorme, mesmo em pequenos volumes. Por exemplo,\(1 \, cm^3\) de um gás no STP contém\(2.68 \times 10^{19} \) moléculas. Mais uma vez, observe que nosso resultado para N é o mesmo para todos os tipos de gases, incluindo misturas.

Como observamos no capítulo sobre mecânica dos fluidos, os pascais também são\(N/m^2\)\(Pa \cdot m^3 = N \cdot m = J\). Assim, nosso resultado para N é adimensional, um número puro que pode ser obtido contando (em princípio) em vez de medir. Como é o número de moléculas, colocamos “moléculas” após o número, tendo em mente que é um auxílio à comunicação e não uma unidade.

Número de Moles e Avogadro

Geralmente, é conveniente medir a quantidade de substância com uma unidade em uma escala mais humana do que as moléculas. A unidade SI para esse fim foi desenvolvida pelo cientista italiano Amedeo Avogadro (1776-1856). (Ele trabalhou a partir da hipótese de que volumes iguais de gás em igual pressão e temperatura contêm números iguais de moléculas, independentemente do tipo de gás. Conforme mencionado acima, essa hipótese foi confirmada quando a aproximação ideal do gás se aplica.) Um mol (abreviado mol) é definido como a quantidade de qualquer substância que contém tantas moléculas quanto átomos em exatamente 12 gramas (0,012 kg) de carbono-12. (Tecnicamente, devemos dizer “unidades de fórmula”, não “moléculas”, mas essa distinção é irrelevante para nossos propósitos.) O número de moléculas em um mol é chamado de número de Avogadro (\(N_A\)) e agora se sabe que o valor do número de Avogadro é\[N_A = 6.02 \times 10^{-23} \, mol^{-1}\]. Agora podemos escrever\(N = N_An\), onde n representa o número de moles de uma substância.

O número de Avogadro relaciona a massa de uma quantidade de substância em gramas com o número de prótons e nêutrons em um átomo ou molécula (12 para um átomo de carbono-12), que determinam aproximadamente sua massa. É natural definir uma unidade de massa de forma que a massa de um átomo seja aproximadamente igual ao seu número de nêutrons e prótons. A unidade desse tipo aceita para uso com o SI é a unidade unificada de massa atômica (u), também chamada de dalton. Especificamente, um átomo de carbono-12 tem uma massa de exatamente 12 u, de modo que sua massa molar M em gramas por mol é numericamente igual à massa de um átomo de carbono-12 em u. Essa igualdade vale para qualquer substância. Em outras palavras, não\(N_A\) é apenas a conversão de números de moléculas em moles, mas também é a conversão de u para gramas:\(6.02 \times 10^{23} \, u = 1 \, g\). Veja a Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Qual é o tamanho de uma toupeira? Em um nível macroscópico, o número de bolas de tênis de mesa de Avogadro cobriria a Terra a uma profundidade de cerca de 40 km.

Exercício\(\PageIndex{1A}\)

A quantidade diária recomendada de vitamina\(B_3\) ou niacina\(C_6NH_5O_2\), para mulheres que não estão grávidas ou amamentando, é de 14 mg. Encontre o número de moléculas de niacina nessa quantidade.

Responda

Primeiro, precisamos calcular a massa molar (a massa de um mol) da niacina. Para fazer isso, devemos multiplicar o número de átomos de cada elemento na molécula pela massa molar do elemento.

(6 mol de carbono) (12,0 g/mol) + (5 mol de hidrogênio) (1,0 g/mol) + (1 mol de nitrogênio) (14 g/mol) + (2 mol de oxigênio) (16,0 g/mol) = 123 g/mol

Em seguida, precisamos calcular o número de moles em 14 mg.

\(\left(\dfrac{14 \, mg}{123 \, g/mol}\right)\left(\dfrac{1 \, g}{1000 \, mg}\right) = 1.14 \times 10^{-4} \, mol.\)

Em seguida, usamos o número de Avogadro para calcular o número de moléculas:

\(N = nN_A = (1.14 \times 10^{-4} \, mol)(6.02 \times 10^{23} \, molecules/mol) = 6.85 \times 10^{19} molecules\)

Exercício\(\PageIndex{1B}\)

A densidade do ar em uma sala de aula\((p = 1.00 \, atm\) e\(T = 20^oC\)) é\(1.28 \, kg/m^3\). Em que pressão está a densidade\(0.600 \, kg/m^3\) se a temperatura for mantida constante?

Responda

A densidade de um gás é igual a uma constante, a massa molecular média, vezes a densidade numérica N/ V. A partir da lei do gás ideal\(pV = Nk_BT\), vemos isso\(N/V = p/k_BT\). Portanto, em temperatura constante, se a densidade e, consequentemente, a densidade numérica forem reduzidas pela metade, a pressão também deverá ser reduzida pela metade,\(p_f = 0.500 \, atm\) e.

A lei do gás ideal reformulada usando toupeiras

Uma expressão muito comum da lei do gás ideal usa o número de moles em uma amostra, n, em vez do número de moléculas, N. Partimos da lei do gás ideal,

\[pV = Nk_BT,\]

e multiplique e divida o lado direito da equação pelo número de Avogadro\(N_A\). Isso nos dá\[pV = \dfrac{N}{N_A}N_A k_BT.\]

Observe que\(n = N/N_A\) é o número de toupeiras. Definimos a constante universal do gás como\(R = N_Ak_B\) e obtemos a lei ideal do gás em termos de moles.

Lei do Gás Ideal (em termos de toupeiras)

Em termos de número de moles n, a lei do gás ideal é escrita como\[pV = nRT.\]

Em unidades SI,

\[R = N_Ak_B = (6.02 \times 10^{23} \, mol^{-1}) (1.38 \times 10^{-23} J/K) = 8.31 \, J/mol \cdot K\]

Em outras unidades,

\[R = 1.99 \dfrac{cal}{mol \cdot K} = 0.0821 \dfrac{L \cdot atm}{mol \cdot K}.\]

Você pode usar qualquer valor de R que seja mais conveniente para um problema específico.

Exemplo\(\PageIndex{3}\): Density of Air at STP and in a Hot Air Balloon

Calcule a densidade do ar seco (a) sob condições padrão e (b) em um balão de ar quente a uma temperatura de\(120^oC\). O ar seco é aproximadamente\(78\% N_2, \, 21\% O_2,\)\(1\% \, Ar\) e.

Estratégia e solução

1. Somos solicitados a encontrar a densidade ou massa por metro cúbico. Podemos começar encontrando a massa molar. Se tivermos cem moléculas, das quais 78 são nitrogênio, 21 são oxigênio e 1 é argônio, a massa molecular média é\(frac{78 \, m_{N_2} + 21 \, m_{O_2} + m_{Ar}}{100}\), ou a massa de cada constituinte multiplicada por sua porcentagem. O mesmo se aplica à massa molar, que, portanto, é\[M = 0.78 \, M_{N_2} + 0,21 \, M_{O_2} + 0.01 \, M_{Ar} = 29.0 \, g/mol.\] Agora podemos encontrar o número de moles por metro cúbico. Usamos a lei do gás ideal em termos de toupeiras\(pV = nRT\),\(p = 1.00 \, atm\)\(T = 273 \, K\), com\(V = 1 \, m^3\),,\(R = 8.31 \, J/mol \cdot K\) e. A escolha mais conveniente para R neste caso é\(R = 8.31 \, J/mol \cdot K\) porque as quantidades conhecidas estão em unidades SI:\[n = \dfrac{pV}{RT} = \dfrac{(1.01 \times 10^5 \, Pa)(1 \, m^3)}{(8.31 \, J/mol \cdot K)(273 \, K)} = 44.5 \, mol.\] Então, a massa\(m_s\) desse ar é\[m_s = nM = (44.5 \, mol)(29.0 \, g/mol) = 1290 \, g = 1.29 \, kg.\] Finalmente, a densidade do ar em STP é\[\rho = \dfrac{m_s}{V} = \dfrac{1.29 \, kg}{1 \, m^3} = 1.29 \, kg/m^3.\]
2. A pressão do ar dentro do balão ainda é de 1 atm porque o fundo do balão está aberto para a atmosfera. O cálculo é o mesmo, exceto que usamos uma temperatura de\(120^oC\), que é 393 K. Podemos repetir o cálculo em (a), ou simplesmente observar que a densidade é proporcional ao número de moles, que é inversamente proporcional à temperatura. Em seguida, usando os subscritos 1 para ar no STP e 2 para o ar quente, temos\[\rho_2 = \dfrac{T_1}{T_2}\rho_1 = \dfrac{273 \, K}{393 \, K}(1.29 \, kg/m^3) = 0.896 \, kg/m^3.\]

Significância

Usando os métodos do Princípio e da Flutuabilidade de Arquimedes, podemos descobrir que a força líquida no\(2200 \, m^3\) ar\(120^oC\) é\(F_b - F_g = \rho_{atmosphere}V_g - \rho_{hot \, air}V_g = 8.49 \times 10^3 \, N\), ou suficiente, para levantar cerca de 867 kg. A densidade de massa e a densidade molar do ar no STP, encontradas acima, são frequentemente números úteis. A partir da densidade molar, podemos facilmente determinar outro número útil, o volume de um mol de qualquer gás ideal no STP, que é 22,4 L.

Exercício\(\PageIndex{3}\)

Líquidos e sólidos têm densidades da ordem de 1000 vezes maiores que os gases. Explique como isso implica que as distâncias entre as moléculas nos gases são da ordem de 10 vezes maiores que o tamanho de suas moléculas.

Responda

A densidade é a massa por unidade de volume e o volume é proporcional ao tamanho de um corpo (como o raio de uma esfera) ao cubo. Portanto, se a distância entre as moléculas aumenta em um fator de 10, o volume ocupado aumenta em um fator de 1000 e a densidade diminui em um fator de 1000. Como assumimos que as moléculas estão em contato em líquidos e sólidos, a distância entre seus centros está na ordem de seu tamanho típico, então a distância nos gases é da ordem de 10 vezes maior.

A lei do gás ideal está intimamente relacionada à energia: as unidades em ambos os lados da equação são joules. O lado direito da equação ideal da lei do gás é\(Nk_BT\). Esse termo é aproximadamente a energia cinética translacional total (que, ao discutir gases, se refere à energia de tradução de uma molécula, não à energia de vibração de seus átomos ou rotação) de N moléculas a uma temperatura absoluta T, como veremos formalmente na próxima seção. O lado esquerdo da equação da lei do gás ideal é pV. Conforme mencionado no exemplo sobre o número de moléculas em um gás ideal, a pressão multiplicada pelo volume tem unidades de energia. A energia de um gás pode ser alterada quando o gás funciona à medida que aumenta em volume, algo que exploramos no capítulo anterior, e a quantidade de trabalho está relacionada à pressão. Esse é o processo que ocorre em motores e turbinas a gasolina ou a vapor, como veremos no próximo capítulo.

Estratégia de resolução de problemas: a lei do gás ideal

• Etapa 1. Examine a situação para determinar se um gás ideal está envolvido. A maioria dos gases é quase ideal, a menos que estejam próximos do ponto de ebulição ou em pressões muito acima da pressão atmosférica.
• Etapa 2. Faça uma lista de quais quantidades são fornecidas ou podem ser inferidas do problema conforme declarado (identifique as quantidades conhecidas).
• Etapa 3. Identifique exatamente o que precisa ser determinado no problema (identifique as quantidades desconhecidas). Uma lista escrita é útil.
• Etapa 4. Determine se o número de moléculas ou o número de moles é conhecido ou solicitado para decidir se deve usar a lei do gás ideal como\( pV = Nk_BT\), onde N é o número de moléculas ou\(pV = nRT\), onde n é o número de moles.
• Etapa 5. Converta valores conhecidos em unidades SI adequadas (K para temperatura, Pa para pressão,\(m^3\) para volume, moléculas para N e moles para n). Se as unidades dos conhecidos forem consistentes com um dos valores não SI de R, você poderá deixá-las nessas unidades. Certifique-se de usar temperatura absoluta e pressão absoluta.
• Etapa 6. Resolva a lei do gás ideal para a quantidade a ser determinada (a quantidade desconhecida). Talvez seja necessário calcular uma proporção entre os estados finais e os estados iniciais para eliminar as quantidades desconhecidas que são mantidas fixas.
• Etapa 7. Substitua as quantidades conhecidas, junto com suas unidades, na equação apropriada e obtenha soluções numéricas completas com unidades.
• Etapa 8. Verifique a resposta para ver se é razoável: Faz sentido?

A equação de estado de Van der Waals

Observamos repetidamente que a lei do gás ideal é uma aproximação. Como isso pode ser melhorado? A equação de estado de van der Waals (em homenagem ao físico holandês Johannes van der Waals, de 1837 a 1923) a melhora levando em consideração dois fatores. Primeiro, as forças de atração entre as moléculas, que são mais fortes em maior densidade e reduzem a pressão, são levadas em consideração adicionando à pressão um termo igual ao quadrado da densidade molar multiplicado por um coeficiente positivo a. Em segundo lugar, o volume das moléculas é representado por uma constante positiva b, que pode ser considerada como o volume de um mol de moléculas. Isso é subtraído do volume total para fornecer o volume restante no qual as moléculas podem se mover. As constantes a e b são determinadas experimentalmente para cada gás. A equação resultante é

\[ \left[p + a\left(\dfrac{n}{V}\right)^2\right] (V - nb) = nRT.\]

No limite da baixa densidade (n pequeno), os termos a e b são insignificantes e temos a lei do gás ideal, como deveríamos para a baixa densidade. Por outro lado, se\(V - nb\) for pequeno, o que significa que as moléculas estão muito próximas umas das outras, a pressão deve ser maior para dar o mesmo NrT, como seria de esperar na situação de um gás altamente comprimido. No entanto, o aumento da pressão é menor do que esse argumento sugeriria, porque em alta densidade o\((n/V)^2\) termo é significativo. Como é positivo, faz com que uma pressão menor forneça o mesmo NrT.

A equação de estado de van der Waals funciona bem para a maioria dos gases sob uma ampla variedade de condições. Como veremos no próximo módulo, ele até prevê a transição gás-líquido.

Diagramas pV

Podemos examinar aspectos do comportamento de uma substância traçando um diagrama de pV, que é um gráfico de pressão versus volume. Quando a substância se comporta como um gás ideal, a lei do gás ideal\(pV = nRT\) descreve a relação entre sua pressão e volume. Em um diagrama de pV, é comum traçar uma isoterma, que é uma curva que mostra p em função de V com o número de moléculas e a temperatura fixos. Então, para um gás ideal,\(pV = constant.\) por exemplo, o volume do gás diminui à medida que a pressão aumenta. O gráfico resultante é uma hipérbole.

No entanto, se assumirmos a equação de estado de van der Waals, as isotermas se tornarão mais interessantes, conforme mostrado na Figura\(\PageIndex{6}\). Em altas temperaturas, as curvas são aproximadamente hipérboles, representando um comportamento aproximadamente ideal em várias temperaturas fixas. Em temperaturas mais baixas, as curvas parecem cada vez menos com hipérbolas, ou seja, o gás não está se comportando de maneira ideal. Há uma temperatura crítica\(T_c\) na qual a curva tem um ponto com inclinação zero. Abaixo dessa temperatura, as curvas não diminuem monotonicamente; em vez disso, cada uma delas tem uma “protuberância”, o que significa que, para uma determinada faixa de volume, aumentar o volume aumenta a pressão.

Figura\(\PageIndex{6}\): Diagrama pV para um gás Van der Waals em várias temperaturas. As curvas vermelhas são calculadas em temperaturas acima da temperatura crítica e as curvas azuis em temperaturas abaixo dela. As curvas azuis têm uma oscilação na qual o volume (V) aumenta com o aumento da temperatura (T), uma situação impossível, então elas devem ser corrigidas como na Figura\(\PageIndex{7}\). (crédito: “Eman” /Wikimedia Commons)

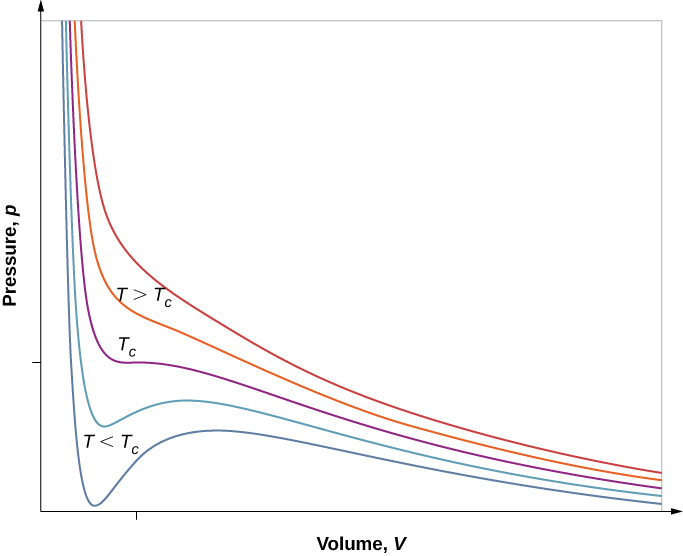
Esse comportamento seria completamente antifísico. Em vez disso, as curvas são entendidas como descrevendo uma transição de fase líquido-gás. A parte oscilante da curva é substituída por uma linha horizontal, mostrando que, à medida que o volume aumenta em temperatura constante, a pressão permanece constante. Esse comportamento corresponde à ebulição e condensação; quando uma substância está em sua temperatura de ebulição para uma pressão específica, ela pode aumentar de volume à medida que parte do líquido se transforma em gás, ou diminuir à medida que parte do gás se transforma em líquido, sem qualquer alteração na temperatura ou pressão.

\(\PageIndex{7}\)A figura mostra isotermas semelhantes que são mais realistas do que aquelas baseadas na equação de van der Waals. As partes íngremes das curvas à esquerda da região de transição mostram a fase líquida, que é quase incompressível — uma pequena diminuição no volume requer um grande aumento na pressão. As partes planas mostram a transição líquido-gás; as regiões azuis que elas definem representam combinações de pressão e volume onde líquido e gás podem coexistir.

Figura\(\PageIndex{7}\): diagramas de pV. (a) Cada curva (isoterma) representa a relação entre p e V a uma temperatura fixa; as curvas superiores estão em temperaturas mais altas. As curvas inferiores não são hipérboles porque o gás não é mais um gás ideal. (b) Uma porção expandida do diagrama pV para baixas temperaturas, onde a fase pode mudar de um gás para um líquido. O termo “vapor” se refere à fase gasosa quando ela existe a uma temperatura abaixo da temperatura de ebulição.

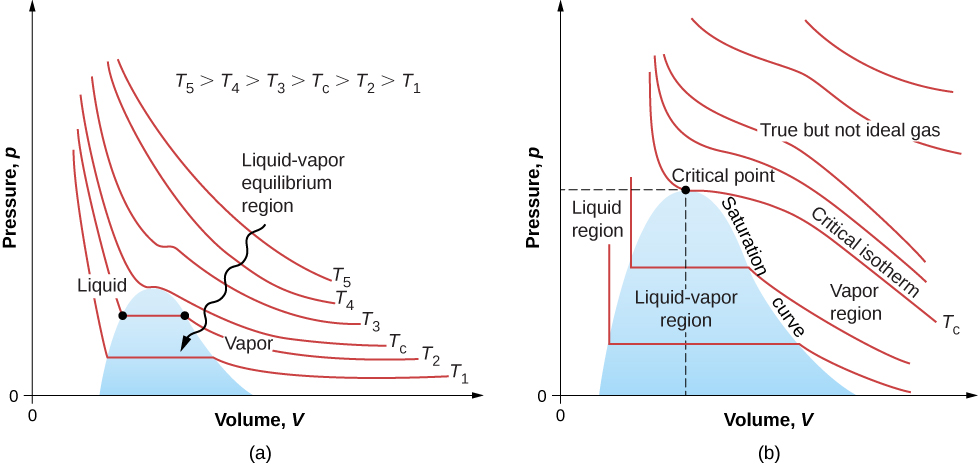
As isotermas acima\(T_c\) não passam pela transição líquido-gás. Portanto, o líquido não pode existir acima dessa temperatura, que é a temperatura crítica (descrita no capítulo sobre temperatura e calor). Com uma pressão suficientemente baixa acima dessa temperatura, o gás tem a densidade de um líquido, mas não se condensa; diz-se que o gás é supercrítico. Em alta pressão, é sólido. O dióxido de carbono, por exemplo, não tem fase líquida a uma temperatura acima\(31.0^oC\). A pressão crítica é a pressão máxima na qual o líquido pode existir. O ponto no diagrama pV na pressão e temperatura críticas é o ponto crítico (sobre o qual você aprendeu no capítulo sobre temperatura e calor). A tabela lista temperaturas e pressões críticas representativas.

Tabela\(\PageIndex{1}\): Temperaturas e pressões críticas para várias substâncias

Substância	Temperatura crítica	\(T_c\)	Pressão crítica
	K	\ (t_C\) ">\(^oC\)	Pa	caixa eletrônico
Água	647,4	\ (t_C\) ">374,3	\(22.12 \times 10^6\)	219,0
Dióxido de enxofre	430,7	\ (t_C\) ">157,6	\(7.88\times 10^6\)	78,0
Amônia	405,5	\ (t_C\) ">132,4	\(11.28\times 10^6\)	111,7
Dióxido de carbono	304.2	\ (t_C\) ">31,1	\(7.39\times 10^6\)	73,2
Oxigênio	154,8	\ (t_C\) ">—118,4	\(5.08\times 10^6\)	50,3
Azoto	126,2	\ (t_C\) ">—146,9	\(3.39\times 10^6\)	33.6
Hidrogênio	33.3	\ (t_C\) ">—239,9	\(1.30\times 10^6\)	12,9
Hélio	5.3	\ (t_C\) ">—267,9	\(0.229\times 10^6\)	2,27