6.2: Radiação de corpo negro
- Page ID
- 182914
Ao final desta seção, você poderá:
- Aplique as leis de Wien e Stefan para analisar a radiação emitida por um corpo negro
- Explique a hipótese de Planck sobre quanta de energia
Todos os corpos emitem radiação eletromagnética em uma faixa de comprimentos de onda. Em um capítulo anterior, aprendemos que um corpo mais frio irradia menos energia do que um corpo mais quente. Também sabemos pela observação que quando um corpo é aquecido e sua temperatura aumenta, o comprimento de onda percebido de sua radiação emitida muda de infravermelho para vermelho, e depois de vermelho para laranja, e assim por diante. Conforme sua temperatura aumenta, o corpo brilha com as cores correspondentes a comprimentos de onda cada vez menores do espectro eletromagnético. Este é o princípio subjacente da lâmpada incandescente: um filamento de metal quente brilha em vermelho e, quando o aquecimento continua, seu brilho eventualmente cobre toda a porção visível do espectro eletromagnético. A temperatura (T) do objeto que emite radiação, ou o emissor, determina o comprimento de onda no qual a energia irradiada está no máximo. Por exemplo, o Sol, cuja temperatura superficial está na faixa entre 5000 K e 6000 K, irradia mais fortemente em uma faixa de comprimentos de onda de cerca de 560 nm na parte visível do espectro eletromagnético. Seu corpo, quando em sua temperatura normal de cerca de 300 K, irradia mais fortemente na parte infravermelha do espectro.
A radiação incidente em um objeto é parcialmente absorvida e parcialmente refletida. Em equilíbrio termodinâmico, a taxa na qual um objeto absorve radiação é a mesma que a taxa na qual ele a emite. Portanto, um bom absorvedor de radiação (qualquer objeto que absorva radiação) também é um bom emissor. Um absorvedor perfeito absorve toda a radiação eletromagnética incidente nele; esse objeto é chamado de corpo negro.

Embora o corpo negro seja uma idealização, porque nenhum objeto físico absorve 100% da radiação incidente, podemos construir uma realização próxima de um corpo negro na forma de um pequeno orifício na parede de um gabinete selado conhecido como radiador de cavidade, conforme mostrado na Figura\(\PageIndex{1}\). As paredes internas de um radiador de cavidade são ásperas e escurecidas, de modo que qualquer radiação que entra por um pequeno orifício na parede da cavidade fica presa dentro da cavidade. No equilíbrio termodinâmico (à temperatura T), as paredes da cavidade absorvem exatamente a mesma quantidade de radiação que emitem. Além disso, dentro da cavidade, a radiação que entra no orifício é equilibrada pela radiação que sai dele. O espectro de emissão de um corpo negro pode ser obtido analisando a luz que irradia do orifício. As ondas eletromagnéticas emitidas por um corpo negro são chamadas de radiação de corpo negro.
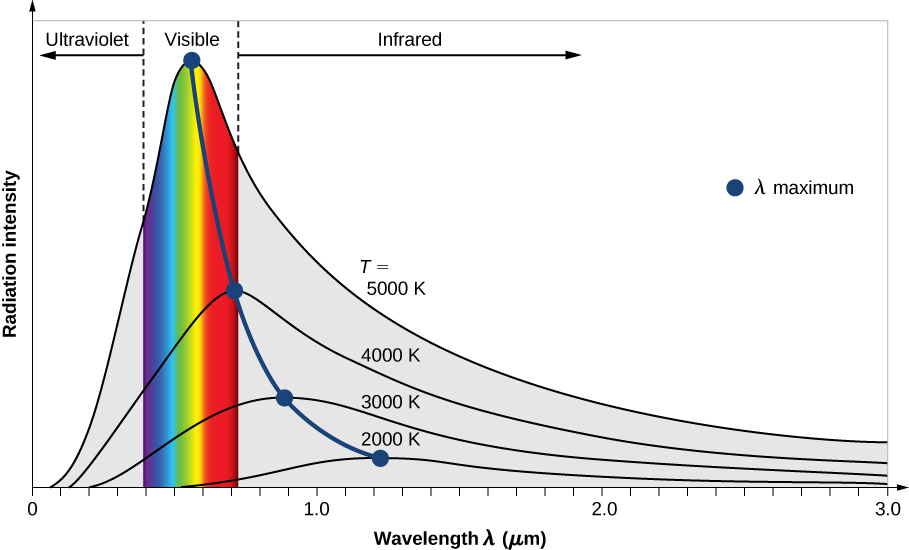
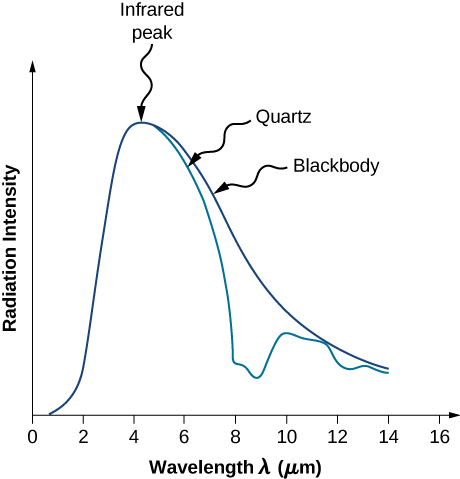
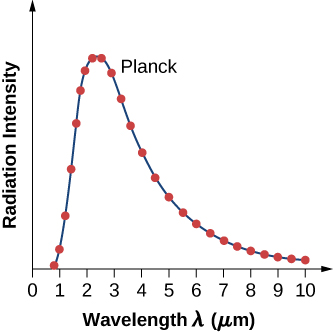
A intensidade\(I(\lambda, T)\) da radiação do corpo negro depende do comprimento\(\lambda\) de onda da radiação emitida e da temperatura T do corpo negro (Figura\(\PageIndex{2}\)). A função\(I(\lambda, T)\) é a intensidade de potência irradiada por unidade de comprimento de onda; em outras palavras, é a potência irradiada por unidade de área do orifício em um radiador de cavidade por unidade de comprimento de onda. De acordo com esta definição,\(I(\lambda, T)d\lambda\) é a potência por unidade de área que é emitida no intervalo de comprimento de onda\(\lambda\) de\(\lambda + d\lambda\) a. A distribuição da intensidade entre os comprimentos de onda da radiação emitida pelas cavidades foi estudada experimentalmente no final do século XIX. Geralmente, a radiação emitida pelos materiais segue apenas aproximadamente a curva de radiação do corpo negro (Figura\(\PageIndex{3}\)); no entanto, os espectros de estrelas comuns seguem a curva de radiação do corpo negro muito de perto.
Duas leis importantes resumem as descobertas experimentais da radiação de corpo negro: a lei de deslocamento de Wien e a lei de Stefan. A lei de deslocamento de Wien é ilustrada na Figura\(\PageIndex{2}\) pela curva que conecta os máximos nas curvas de intensidade. Nessas curvas, vemos que quanto mais quente o corpo, menor o comprimento de onda correspondente ao pico de emissão na curva de radiação. Quantitativamente, a lei de Wien diz
\[\lambda_{max}T = 2.898 \times 10^{-3} m \cdot K \label{Wien} \]
onde\(\lambda_{max}\) é a posição do máximo na curva de radiação. Em outras palavras,\(\lambda_{max}\) é o comprimento de onda no qual um corpo negro irradia mais fortemente a uma determinada temperatura T. Observe que na Equação\ ref {Wien}, a temperatura está em kelvins. A lei de deslocamento de Wien nos permite estimar as temperaturas de estrelas distantes medindo o comprimento de onda da radiação que elas emitem.
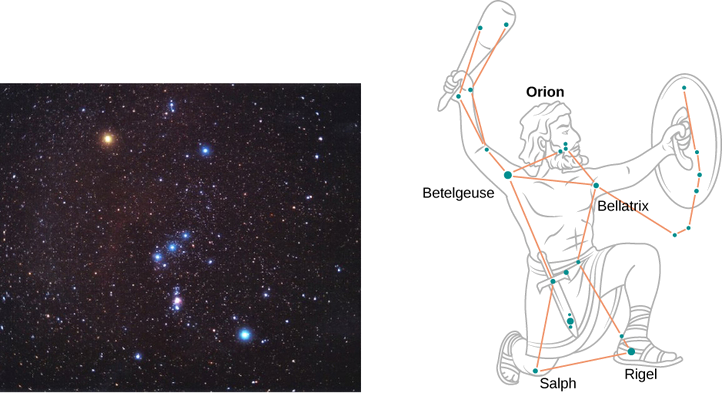
Em uma noite clara durante os meses de inverno, se você estiver no hemisfério norte e olhar para o céu, poderá ver a constelação de Orion (O Caçador). Uma estrela nesta constelação, Rigel, pisca em azul e outra estrela, Betelgeuse, tem uma cor avermelhada, conforme mostrado na Figura\(\PageIndex{4}\). Qual dessas duas estrelas é mais fria, Betelgeuse ou Rigel?
Estratégia
Tratamos cada estrela como um corpo negro. Então, de acordo com a lei de Wien, sua temperatura é inversamente proporcional ao comprimento de onda de seu pico de intensidade. O comprimento\(\lambda_{max}^{(blue)}\) de onda da luz azul é menor do que o comprimento\(\lambda_{max}^{(red)}\) de onda da luz vermelha. Mesmo que não saibamos os comprimentos de onda precisos, ainda podemos configurar uma proporção.
Solução
Escrevendo a lei de Wien para a estrela azul e para a estrela vermelha, temos
\[\begin {align*} \lambda_{max}^{(red)}T_{(red)} &= 2.898 \times 10^{-3} m \cdot K \\[5pt] &= \lambda_{max}^{(blue)} T_{(blue)} \end{align*} \nonumber \]
Quando simplificado, isso dá
\[T_{(red)} = \dfrac{\lambda_{max}^{(blue)}}{\lambda_{max}^{(red)}}T_{(blue)} < T_{(blue)} \nonumber \]
Portanto, Betelgeuse é mais legal que Rigel.
Significância
Observe que a lei de deslocamento de Wien nos diz que quanto maior a temperatura de um corpo emissor, menor o comprimento de onda da radiação que ele emite. A análise qualitativa apresentada neste exemplo geralmente é válida para qualquer corpo emissor, seja um objeto grande, como uma estrela, ou um objeto pequeno, como o filamento brilhante em uma lâmpada incandescente.
A chama de uma vela com aroma de pêssego tem uma cor amarelada e a chama do queimador de Bunsen em um laboratório de química tem uma cor azulada. Qual chama tem uma temperatura mais alta?
- Resposta
A segunda relação experimental é a lei de Stefan, que diz respeito à potência total da radiação do corpo negro emitida em todo o espectro de comprimentos de onda a uma determinada temperatura. No\(\PageIndex{2}\), essa potência total é representada pela área abaixo da curva de radiação do corpo negro para um determinado T. À medida que a temperatura de um corpo negro aumenta, a potência total emitida também aumenta. Quantitativamente, a lei de Stefan expressa essa relação como
\[P(T) = \sigma AT^4 \nonumber \]
onde\(A\) está a área da superfície de um corpo negro,\(T\) é sua temperatura (em kelvins) e\(σ\) é a constante de Stefan-Boltzmann,\(\sigma = 5.670 \times 10^{-8} W/(m^2 \cdot K^4)\). A lei de Stefan nos permite estimar quanta energia uma estrela está irradiando medindo remotamente sua temperatura.
Uma estrela como o nosso Sol eventualmente evoluirá para uma estrela “gigante vermelha” e depois para uma estrela “anã branca”. Uma anã branca típica tem aproximadamente o tamanho da Terra e sua temperatura superficial é de aproximadamente\(2.5 \times 10^4 K\). Uma gigante vermelha típica tem uma temperatura superficial\(3.0 \times 10^3 K\) e um raio ~ 100.000 vezes maior do que o de uma anã branca. Qual é a potência média irradiada por unidade de área e a potência total irradiada por cada um desses tipos de estrelas? Como eles se comparam?
Estratégia
Se tratarmos a estrela como um corpo negro, então, de acordo com a lei de Stefan, a potência total que a estrela irradia é proporcional à quarta potência de sua temperatura. Para encontrar a potência irradiada por unidade de área da superfície, não precisamos fazer nenhuma suposição sobre a forma da estrela porque P/A depende apenas da temperatura. No entanto, para calcular a potência total, precisamos supor que a energia irradia através de uma superfície esférica envolvendo a estrela, de modo que a área da superfície seja\(A = 4\pi R^2\), onde R é seu raio.
Solução
Uma proporção simples baseada na lei de Stefan dá
\[\dfrac{P_{dwarf}/A_{dwarf}}{P_{giant}/A_{giant}} = \dfrac{\sigma T_{dwarf}^4}{\sigma T_{giant}^4} = \left(\dfrac{T_{dwarf}}{T_{giant}}\right)^4 = 4820 \label{6.5} \]
A potência emitida por unidade de área por uma anã branca é cerca de 5000 vezes a energia emitida por uma gigante vermelha. Denotando essa razão por\(a=4.8×10^3\), a equação\ ref {6.5} fornece
\[\dfrac{P_{dwarf}}{P_{giant}} = \alpha \dfrac{A_{dwarf}}{A_{giant}} = \alpha \dfrac{4\pi R_{dwarf}^2}{4\pi R_{giant}^2} = \alpha \left( \dfrac{R_{dwarf}}{R_{giant}} \right)^2 = 4.8 \times 10^{−7} \nonumber \]
Vemos que a potência total emitida por uma anã branca é uma pequena fração da potência total emitida por uma gigante vermelha. Apesar de sua temperatura relativamente mais baixa, a potência geral irradiada por uma gigante vermelha excede em muito a da anã branca porque a gigante vermelha tem uma área de superfície muito maior. Para estimar o valor absoluto da potência emitida por unidade de área, usamos novamente a lei de Stefan. Para a anã branca, obtemos
\[\dfrac{P_{dwarf}}{A_{dwarf}} = \sigma T_{dwarf}^4 = 5.670 \times 10^{-8} \dfrac{W}{m^2 \cdot K^4} (2.5 \times 10^4 \, K)^4 = 2.2 \times 10^{10} \dfrac{W}{m^2} \label{6.7} \]
O resultado análogo para a gigante vermelha é obtido escalando o resultado para uma anã branca:
\[\dfrac{P_{giant}}{A_{giant}} = \dfrac{2.2 \times 10^{10}}{4.82 \times 10^3} \dfrac{W}{m^2} = 4.56 \times 10^6 \dfrac{W}{m^2} \cong 4.6 \times 10^{-6} \dfrac{W}{m^2} \nonumber \]
Significância
Para estimar a potência total emitida por uma anã branca, em princípio, poderíamos usar a Equação\ ref {6.7}. No entanto, para encontrar sua área de superfície, precisamos saber o raio médio, o que não é dado neste exemplo. Portanto, a solução termina aqui. O mesmo vale para a estrela gigante vermelha.
Um pôquer de ferro está sendo aquecido. À medida que a temperatura sobe, o pôquer começa a brilhar — primeiro vermelho opaco, depois vermelho brilhante, depois laranja e depois amarelo. Use a curva de radiação do corpo negro ou a lei de Wien para explicar essas mudanças na cor do brilho.
- Resposta
-
O comprimento de onda do máximo de radiação diminui com o aumento da temperatura.
Suponha que duas estrelas\(α\) e\(β\), irradiem exatamente a mesma potência total. Se o raio da estrela\(α\) for três vezes maior que o da estrela\(β\), qual é a proporção das temperaturas da superfície dessas estrelas? Qual é o mais quente?
- Resposta
-
\(T_{\alpha}/T_{\beta} = 1/\sqrt{3} \cong 0.58\), então a estrela\(\beta\) está mais quente.
O termo “corpo negro” foi cunhado por Gustav R. Kirchhoff em 1862. A curva de radiação do corpo negro era conhecida experimentalmente, mas sua forma escapou da explicação física até o ano de 1900. O modelo físico de um corpo negro à temperatura T é o das ondas eletromagnéticas encerradas em uma cavidade (Figura\(\PageIndex{1}\)) e em equilíbrio termodinâmico com as paredes da cavidade. As ondas podem trocar energia com as paredes. O objetivo aqui é encontrar a distribuição da densidade de energia entre vários modos de vibração em vários comprimentos de onda (ou frequências). Em outras palavras, queremos saber quanta energia é transportada por um único comprimento de onda ou por uma faixa de comprimentos de onda. Depois de conhecermos a distribuição de energia, podemos usar métodos estatísticos padrão (semelhantes aos estudados em um capítulo anterior) para obter a curva de radiação do corpo negro, a lei de Stefan e a lei de deslocamento de Wien. Quando o modelo físico está correto, as previsões teóricas devem ser as mesmas das curvas experimentais.
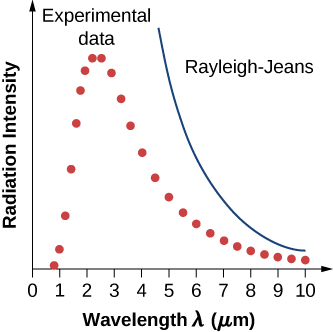
Em uma abordagem clássica do problema da radiação do corpo negro, na qual a radiação é tratada como ondas (como você estudou nos capítulos anteriores), os modos das ondas eletromagnéticas presas na cavidade estão em equilíbrio e trocam continuamente suas energias com as paredes da cavidade. Não há nenhuma razão física para que uma onda faça o contrário: qualquer quantidade de energia pode ser trocada, seja sendo transferida da onda para o material na parede ou sendo recebida pela onda do material na parede. Esta imagem clássica é a base do modelo desenvolvido por Lord Rayleigh e, de forma independente, por Sir James Jeans. O resultado desse modelo clássico para curvas de radiação de corpo negro é conhecido como lei de Rayleigh-Jeans. No entanto, conforme mostrado na Figura\(\PageIndex{5}\), a lei Rayleigh-Jeans não reproduz corretamente os resultados experimentais. No limite de comprimentos de onda curtos, a lei de Rayleigh-Jeans prevê uma intensidade de radiação infinita, o que é inconsistente com os resultados experimentais nos quais a intensidade da radiação tem valores finitos na região ultravioleta do espectro. Essa divergência entre os resultados da teoria clássica e dos experimentos, que passou a ser chamada de catástrofe ultravioleta, mostra como a física clássica falha em explicar o mecanismo da radiação do corpo negro.
O problema da radiação do corpo negro foi resolvido em 1900 por Max Planck. Planck usou a mesma ideia do modelo Rayleigh-Jeans no sentido de tratar as ondas eletromagnéticas entre as paredes dentro da cavidade de forma clássica e assumiu que a radiação está em equilíbrio com as paredes da cavidade. A ideia inovadora que Planck introduziu em seu modelo é a suposição de que a radiação da cavidade se origina de oscilações atômicas dentro das paredes da cavidade e que essas oscilações podem ter apenas valores discretos de energia. Portanto, a radiação aprisionada dentro das paredes da cavidade pode trocar energia com as paredes somente em quantidades discretas. A hipótese de Planck de valores discretos de energia, que ele chamou de quanta, pressupõe que os osciladores dentro das paredes da cavidade tenham energias quantizadas. Essa foi uma ideia totalmente nova que foi além da física clássica do século XIX porque, como você aprendeu em um capítulo anterior, na imagem clássica, a energia de um oscilador pode assumir qualquer valor contínuo. Planck assumiu que a energia de um oscilador (\(E_n\)) só pode ter valores discretos ou quantizados:
\[E_n = nhf, \, where \, n = 1,2,3, \ldots \label{eq30} \]
Na Equação\ ref {eq30},\(f\) é a frequência do oscilador de Planck. O número natural\(n\) que enumera essas energias discretas é chamado de número quântico. A constante física\(h\) é chamada de constante de Planck:
\[h = 6.626 \times 10^{-34} J \cdot s = 4.136 \times 10^{-15} eV \cdot s \label{6.10} \]
Cada valor discreto de energia corresponde a um estado quântico de um oscilador de Planck. Os estados quânticos são enumerados por números quânticos. Por exemplo, quando o oscilador de Planck está em seu primeiro estado\(n 1\) quântico, sua energia está\(E_1 = hf\); quando está no estado\(n = 2\) quântico, sua energia está\(E_2 = 2hf\); quando está no estado\(n = 3\) quântico\(E_3 = 3hf\); e assim por diante.
Note que a Equação\ ref {eq30} mostra que há infinitos estados quânticos, que podem ser representados como uma sequência {hf, 2 hf, 3 hf,..., (n — 1) hf, nhf, (n + 1) hf,...}. Cada dois estados quânticos consecutivos nesta sequência são separados por um salto de energia,\(\delta E = hf\). Um oscilador na parede pode receber energia da radiação na cavidade (absorção) ou pode liberar energia para a radiação na cavidade (emissão). O processo de absorção envia o oscilador para um estado quântico superior e o processo de emissão envia o oscilador para um estado quântico inferior. Seja qual for o caminho dessa troca de energia, a menor quantidade de energia que pode ser trocada é hf. Não há limite máximo para a quantidade de energia que pode ser trocada, mas tudo o que é trocado deve ser um múltiplo inteiro de hf. Se o pacote de energia não tiver essa quantidade exata, ele não será absorvido nem emitido na parede do corpo negro.
A hipótese de Planck de quanta de energia afirma que a quantidade de energia emitida pelo oscilador é transportada pelo quantum da radiação,\(\Delta E\):
\[\Delta E = hf \label{planck} \]
Lembre-se de que a frequência da radiação eletromagnética está relacionada ao seu comprimento de onda e à velocidade da luz pela relação fundamental\(f\lambda = c\). This means that we can express Equação\ ref {6.10} equivalentemente em termos de comprimento de onda\(\lambda\). When included in the computation of the energy density of a blackbody, Planck’s hypothesis gives the following theoretical expression for the power intensity of emitted radiation per unit wavelength:
\[I(\lambda, T) = \dfrac{2\pi hc^2}{\lambda^5} \dfrac{1}{e^{hc/\lambda k_BT} - 1} \label{6.11} \]
onde c é a velocidade da luz no vácuo e kBkB é a constante de Boltzmann,\(k_B = 1.380 \times 10^{-23} J/K\). A fórmula teórica expressa na Equação\ ref {6.11} é chamada de lei de radiação de corpo negro de Planck. Essa lei está de acordo com a curva experimental de radiação de corpo negro (Figura\(\PageIndex{2}\)). Além disso, a lei de deslocamento de Wien e a lei de Stefan podem ser derivadas da Equação\ ref {6.11}. Para derivar a lei de deslocamento de Wien, usamos o cálculo diferencial para encontrar o máximo da curva de intensidade de radiação\(I(\lambda, T)\). Para derivar a lei de Stefan e encontrar o valor da constante de Stefan-Boltzmann, usamos cálculo integral e integração\(I(\lambda, T)\) para encontrar a potência total irradiada por um corpo negro a uma temperatura em todo o espectro de comprimentos de onda\(\lambda = 0\) de\(\lambda = \infty\) a. Essa derivação é deixada como um exercício mais adiante neste capítulo.
Um oscilador quântico na parede da cavidade na Figura\(\PageIndex{1}\) está vibrando a uma frequência de\(5.0 \times 10^{14} Hz\). Calcule o espaçamento entre seus níveis de energia.
Estratégia
Os estados de energia de um oscilador quântico são dados pela Equação\ ref {eq30}. O espaçamento de energia\(\Delta E\) é obtido encontrando a diferença de energia entre dois estados quânticos adjacentes para números quânticos n + 1 e n.
Solução
Podemos substituir a frequência dada e a constante de Planck diretamente na equação:
\[\begin {align*} \Delta E &= E_{n + 1} − En = (n + 1)hf − nhf \\[5pt] &= hf \\[5pt] &= (6.626 \times 10^{−34} \, J \cdot s)(5.0 \times 10^{14} \, Hz) \\[5pt] &= 3.3 \times 10^{− 19} \, J \end{align*} \nonumber \]
Significância
Observe que não especificamos que tipo de material foi usado para construir a cavidade. Aqui, um oscilador quântico é um modelo teórico de um átomo ou molécula de material na parede.
Uma molécula está vibrando com uma frequência de\(5.0 \times 10^{14}\, Hz\). Qual é o menor espaçamento entre seus níveis de energia vibracional?
- Resposta
-
\(3.3 \times 10^{-19} J\)
Uma massa de 1,0 kg oscila no final de uma mola com uma constante de mola de 1000 N/m. A amplitude dessas oscilações é de 0,10 m. Use o conceito de quantização para encontrar o espaçamento de energia para este oscilador clássico. A quantização de energia é significativa para sistemas macroscópicos, como esse oscilador?
Estratégia
Usamos a Equação\ ref {planck} como se o sistema fosse um oscilador quântico, mas com a frequência f da massa vibrando em uma mola. Para avaliar se a quantização tem ou não um efeito significativo, comparamos o espaçamento de energia quântica com a energia total macroscópica desse oscilador clássico.
Solução
Para a constante da mola\(k = 1.0 \times 10^3 N/m\),, a frequência f da massa,\(m = 1.0 \, kg\), é
\[f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}} = \dfrac{1}{2\pi} \sqrt{\dfrac{1.0 \times 10^3 N/m}{1.0 \, kg}} \simeq 5.0 \, Hz \nonumber \]
O quantum de energia que corresponde a essa frequência é
\[\Delta E = hf = (6.626 \times 10^{-34} J \cdot s)(5.0 \, Hz) = 3.3 \times 10^{-33} J \nonumber \]
Quando as vibrações têm amplitude\(A = 0.10 \, m\), a energia das oscilações é
\[E = \dfrac{1}{2} kA^2 = \dfrac{1}{2}(1000 \, N/m)(0.1 \, m)^2 = 5.0 \, J \nonumber \]
Significância
Assim, para um oscilador clássico, temos\(\Delta E/E \approx 10^{-34}\). Vemos que a separação dos níveis de energia é incomensuravelmente pequena. Portanto, para todos os fins práticos, a energia de um oscilador clássico assume valores contínuos. É por isso que os princípios clássicos podem ser aplicados aos sistemas macroscópicos encontrados na vida cotidiana sem perda de precisão.
O resultado no Exemplo\(\PageIndex{4}\) seria diferente se a massa não fosse 1,0 kg, mas uma massa minúscula de 1,0 µ g e a amplitude das vibrações fosse 0,10 µ m?
- Resposta
-
Não, porque então\(\Delta E /E \approx 10^{-21}\)
Quando Planck publicou seu resultado pela primeira vez, a hipótese de quanta de energia não foi levada a sério pela comunidade física porque não decorria de nenhuma teoria física estabelecida na época. Foi percebido, até mesmo pelo próprio Planck, como um truque matemático útil que levou a um bom “ajuste” teórico à curva experimental. Essa percepção foi alterada em 1905, quando Einstein publicou sua explicação sobre o efeito fotoelétrico, na qual deu um novo significado ao quantum de energia de Planck: o de uma partícula de luz.


