Skip to main content
Global

2.8: A lupa simples

  1. Last updated
  2. Save as PDF
  • Page ID
    183267

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    Ao final desta seção, você poderá:

    • Entenda a ótica de uma lupa simples
    • Caracterize a imagem criada por uma lupa simples

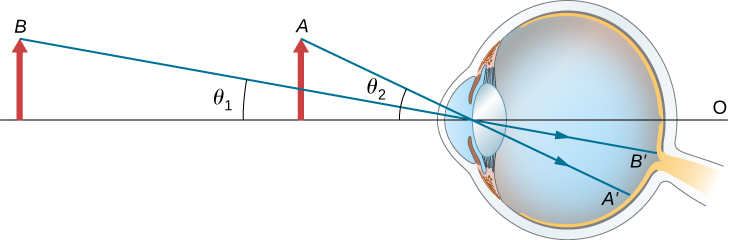
    O tamanho aparente de um objeto percebido pelo olho depende do ângulo que o objeto subtende do olho. Conforme mostrado na Figura\(\PageIndex{1}\), o objeto em\(A\) subtende um ângulo maior em relação ao olho do que quando está posicionado no ponto\(B\). Assim, o objeto em\(A\) forma uma imagem maior na retina (veja\(OA′\)) do que quando está posicionado em\(B\) (veja\(OB′\)). Assim, objetos que subtendem grandes ângulos do olho parecem maiores porque formam imagens maiores na retina.

    Dois objetos do mesmo tamanho são mostrados na frente de um olho. O objeto A está mais próximo do olho e forma um ângulo teta 2 com o eixo óptico. O objeto B está mais distante e forma um ângulo teta 1 com o eixo óptico. Dentro do olho, os raios atingem a retina. O raio B primo está mais próximo do eixo óptico do que o raio A primo.
    Figura\(\PageIndex{1}\): O tamanho percebido por um olho é determinado pelo ângulo subtendido pelo objeto. Uma imagem formada na retina por um objeto em\(A\) é maior do que uma imagem formada na retina pelo mesmo objeto posicionado em B (comparada\(OA′\) a altura da imagem com\(OB′\)).

    Vimos que, quando um objeto é colocado dentro de uma distância focal de uma lente convexa, sua imagem é virtual, vertical e maior que o objeto (veja a parte (b) desta Figura). Assim, quando essa imagem produzida por uma lente convexa serve como objeto para o olho, conforme mostrado na Figura\(\PageIndex{2}\), a imagem na retina é ampliada, porque a imagem produzida pela lente subtende um ângulo maior no olho do que o objeto. Uma lente convexa usada para essa finalidade é chamada de lupa ou lupa simples.

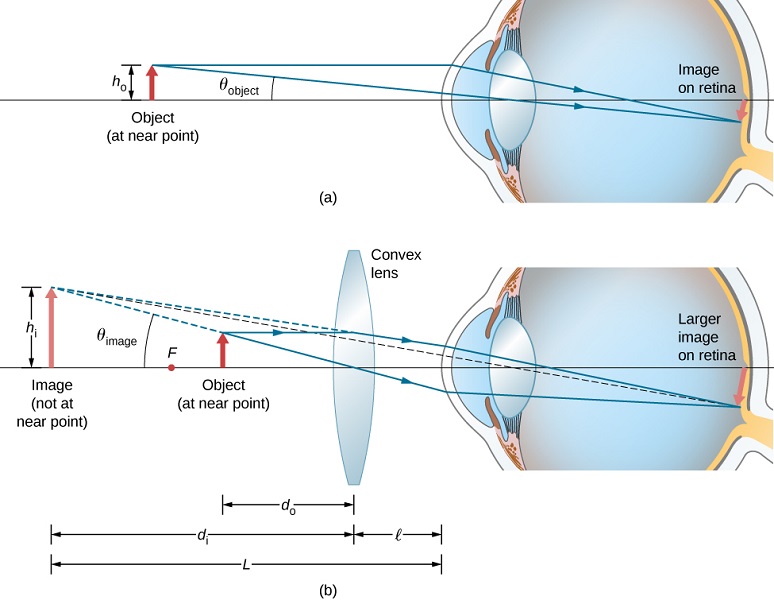
    A Figura a mostra um objeto com altura h 0 na frente de um olho, no ponto próximo. Uma imagem menor que o objeto é formada na retina. A Figura b mostra uma lente biconvexa entre o olho e o objeto. Os raios do objeto passam por isso e entram no olho para formar uma imagem maior na retina. As extensões traseiras dos raios desviados pela lente convergem para trás do objeto para formar uma imagem maior do que o objeto. A distância desta imagem da lente é d subscrito i e a do objeto da lente é d subscrito o. A distância da lente do olho é l. A distância da imagem do olho é L. A altura da imagem é h subscrito i.
    Figura\(\PageIndex{2}\): A lupa simples é uma lente convexa usada para produzir uma imagem ampliada de um objeto na retina. (a) Sem lente convexa, o objeto subtende um ângulo\(θ_{object}\) do olho. (b) Com a lente convexa no lugar, a imagem produzida pela lente convexa subtende um ângulo\(θ_{image}\) do olho, com\(θ_{image}> θ_{object}\). Assim, a imagem na retina é maior com a lente convexa no lugar.

    Para contabilizar a ampliação de uma lente de aumento, comparamos o ângulo subtendido pela imagem (criado pela lente) com o ângulo subtendido pelo objeto (visualizado sem lente), conforme mostrado na Figura\(\PageIndex{1a}\). Assumimos que o objeto está situado no ponto próximo do olho, porque essa é a distância do objeto na qual o olho nu pode formar a maior imagem na retina. Compararemos as imagens ampliadas criadas por uma lente com esse tamanho máximo de imagem a olho nu. A ampliação de uma imagem quando observada a olho nu é a ampliação angular\(M\), que é definida pela razão entre o ângulo\(θ_{image}\) subtendido pela imagem e o ângulo\(θ_{object}\) subtendido pelo objeto:

    \[M=\dfrac{θ_{image}}{θ_{object}}. \nonumber \]

    Considere a situação mostrada na Figura\(\PageIndex{1b}\). A lente de aumento é mantida a uma\(ℓ\) distância do olho e a imagem produzida pela lente de aumento se distancia\(L\) do olho. Queremos calcular a ampliação angular para qualquer arbitrário\(L\)\(ℓ\) e. Na aproximação de ângulo pequeno, o tamanho angular\(θ_{image}\) da imagem é\(h_i/L\). O tamanho angular\(θ_{object}\) do objeto no ponto próximo é\(θ_{object}=h_o/25\,cm\). A ampliação angular é então

    \[\underbrace{ M=\dfrac{θ_{image}}{θ_{object}}=\dfrac{h_i(25cm)}{Lh_o}}_{\text{angular magnification}} . \label{angular magnification} \]

    Usando a definição de ampliação linear

    \[m=−\dfrac{d_i}{d_o}=\dfrac{h_i}{h_o} \label{mag} \]

    e a equação da lente fina

    \[\dfrac{1}{d_o}+\dfrac{1}{d_i}=\dfrac{1}{f} \nonumber \]

    chegamos à seguinte expressão para a ampliação angular de uma lente de aumento:

    \[\begin{align} M&= \left(−\dfrac{d_i}{d_o}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &=−d_i\left(\dfrac{1}{f}−\dfrac{1}{d_i}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &= \left(1−\dfrac{d_i}{f}\right)\left(\dfrac{25\,cm}{L}\right) \label{eq10} \end{align} \]

    Na Figura\(\PageIndex{1b}\), vemos que o valor absoluto da distância da imagem é\(|d_i|=L−ℓ\). Observe que\(d_i<0\), como a imagem é virtual, podemos dispensar o valor absoluto inserindo explicitamente o sinal de menos:

    \[−d_i=L−ℓ. \label{eq34} \]

    Inserindo a Equação\ ref {eq34} na Equação\ ref {eq10} nos dá a equação final para a ampliação angular de uma lente de aumento:

    \[M=\left(\dfrac{25\,cm}{L}\right) \left(1+\dfrac{L−ℓ}{f} \right). \label{eq12} \]

    Observe que todas as quantidades nessa equação devem ser expressas em centímetros. Muitas vezes, queremos que a imagem esteja a uma distância próxima do ponto (por exemplo,\(L=25\,cm\)) para obter a máxima ampliação e mantemos a lente de aumento perto do olho (\(ℓ=0\)). Nesse caso, a Equação\ ref {eq12} fornece

    \[M=1+\dfrac{25\,cm}{f} \label{eq13} \]

    o que mostra que a maior ampliação ocorre na lente com a menor distância focal. Além disso, quando a imagem está à distância do ponto próximo e a lente é mantida perto do olho (\(ℓ=0\)), então\(L=d_i=25\,cm\) a Equação\ ref {eq12} se torna

    \[M=\dfrac{h_i}{h_o}=m \label{eq14} \]

    onde\(m\) está a ampliação linear (Equação\ ref {mag}) derivada anteriormente para espelhos esféricos e lentes finas. Outra situação útil é quando a imagem está no infinito (\(L=\infty\)). A equação\ ref {eq12} então assume a forma

    \[M(L=\infty)=\dfrac{25\,cm}{f}. \label{eq15} \]

    A ampliação resultante é simplesmente a razão entre a distância do ponto próximo e a distância focal da lente de aumento, portanto, uma lente com uma distância focal mais curta oferece uma ampliação mais forte. Embora essa ampliação seja menor em 1 do que a ampliação obtida com a imagem no ponto próximo, ela oferece as condições de visualização mais confortáveis, pois o olho fica relaxado ao visualizar um objeto distante.

    Ao comparar as equações\ ref {eq13} e\ ref {eq15}, vemos que a faixa de ampliação angular de uma determinada lente convergente é

    \[\dfrac{25cm}{f} ≤ M ≤1+\dfrac{25cm}{f}. \nonumber \]

    Exemplo\(\PageIndex{1}\): Magnifying a Diamond

    Um joalheiro deseja inspecionar um diamante de 3,0 mm de diâmetro com uma lupa. O diamante é segurado no ponto próximo do joalheiro (25 cm) e o joalheiro segura a lente de aumento perto do olho.

    1. Qual deve ser a distância focal da lente de aumento para ver uma imagem de 15 mm de diâmetro do diamante?
    2. Qual deve ser a distância focal da lente de aumento para obter uma ampliação de 10x?

    Estratégia

    Precisamos determinar a ampliação necessária da lupa. Como o joalheiro segura a lente de aumento perto do olho, podemos usar a Equação\ ref {eq13} para encontrar a distância focal da lente de aumento.

    Solução

    a. A ampliação linear necessária é a razão entre o diâmetro da imagem desejado e o diâmetro real do diamante (Equação\ ref {eq15}). Como o joalheiro segura a lente de aumento perto de seu olho e a imagem se forma em seu ponto próximo, a ampliação linear é a mesma que a ampliação angular, então

    \[\begin{align*} M &=m=\dfrac{h_i}{h_o}\\[4pt] &=\dfrac{15\,mm}{3.0\,mm} \\[4pt] &=5.0.\end{align*} \nonumber \]

    A distância focal f da lente de aumento pode ser calculada resolvendo a Equação\ ref {eq13} for\(f\), que fornece

    \[M=1+\dfrac{25\,cm}{f} \nonumber \]

    \[\begin{align*} f&=\dfrac{25\,cm}{M−1} \\[4pt] &= \dfrac{25\,cm}{5.0−1} \\[4pt] &= 6.3\,cm \end{align*} \nonumber \]

    b. Para obter uma imagem ampliada por um fator de dez, resolvemos novamente a Equação\ ref {eq13} para\(f\), mas desta vez usamos\(M=10\). O resultado é

    \[\begin{align*} f &=\dfrac{25\,cm}{M−1} \\[4pt] &=\dfrac{25\,cm}{10−1} \\[4pt] &=2.8\,cm. \end{align*} \nonumber \]

    Significância

    Observe que uma ampliação maior é obtida usando uma lente com uma distância focal menor. Portanto, precisamos usar uma lente com raios de curvatura menores que alguns centímetros e mantê-la bem perto de nossos olhos. Isso não é muito conveniente. Um microscópio composto, explorado na seção a seguir, pode superar essa desvantagem.