31.5: Meia-vida e atividade

Objetivos de

Ao final desta seção, você poderá:

• Defina meia-vida.
• Defina namoro.
• Calcule a idade de objetos antigos por datação radioativa.

Os núcleos instáveis decaem. No entanto, alguns nuclídeos decaem mais rápido do que outros. Por exemplo, o rádio e o polônio, descobertos pelos Curies, decaem mais rápido que o urânio. Isso significa que eles têm vida útil mais curta, produzindo uma maior taxa de decaimento. Nesta seção, exploramos meia-vida e atividade, os termos quantitativos para vida útil e taxa de decaimento.

Meia-vida

Por que usar um termo como meia-vida em vez de vida? A resposta pode ser encontrada examinando a Figura\(\PageIndex{1}\), que mostra como o número de núcleos radioativos em uma amostra diminui com o tempo. O tempo em que metade do número original de núcleos decaem é definido como meia-vida.\(t_{1/2}\). Metade dos núcleos restantes decaem na próxima meia-vida. Além disso, metade dessa quantidade decai na meia-vida seguinte. Portanto, o número de núcleos radioativos diminui de\(N\) para\(N/2\) em uma meia-vida, depois para\(N/4\) na próxima e para\(N/8\) na próxima, e assim por diante. Se\(N\) for um número grande, muitas meias-vidas (não apenas duas) passam antes que todos os núcleos se decomponham. A decadência nuclear é um exemplo de processo puramente estatístico. Uma definição mais precisa de meia-vida é que cada núcleo tem 50% de chance de viver por um tempo igual a uma meia-vida\(t_{1/2}\). Assim, se\(N\) for razoavelmente grande, metade dos núcleos originais decaem em um tempo de meia-vida. Se um núcleo individual sobreviver a esse tempo, ele ainda tem 50% de chance de sobreviver por outra meia-vida. Mesmo que sobreviva a centenas de meias-vidas, ainda tem 50% de chance de sobreviver com mais uma. A probabilidade de decaimento é a mesma, não importa quando você começa a contar. É como jogar moedas aleatoriamente. A chance de ter cabeças é de 50%, não importa o que tenha acontecido antes.

Figura\(\PageIndex{1}\): O decaimento radioativo reduz o número de núcleos radioativos ao longo do tempo. Em uma meia-vida,\(t_{1/2}\) o número diminui para metade do seu valor original. Metade do que resta se decompõe na próxima meia-vida, e metade na próxima, e assim por diante. Este é um decaimento exponencial, como visto no gráfico do número de núcleos presentes em função do tempo.

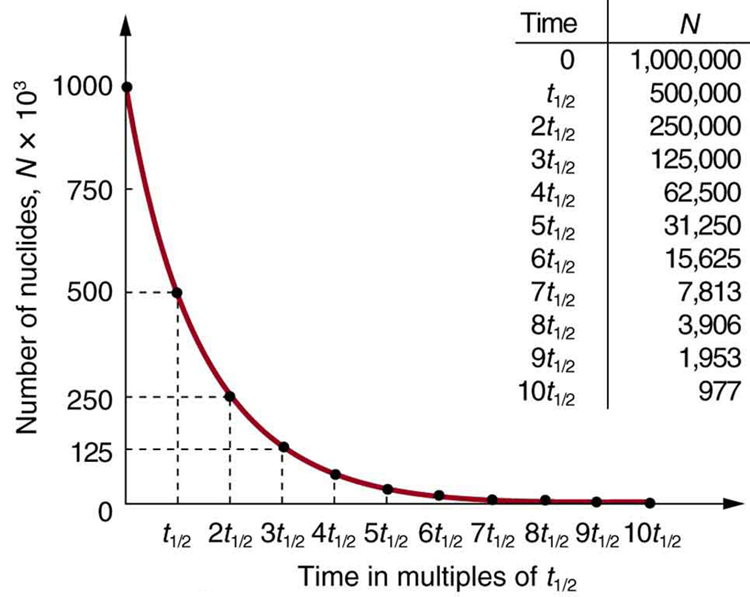
Há uma enorme variação nas meias-vidas de vários nuclídeos, de tão curto quanto\(10^{-23}\) s para os mais instáveis, até mais de\(10^{16}\) y para os menos instáveis, ou cerca de 46 ordens de magnitude. Nuclídeos com meia-vida mais curta são aqueles para os quais as forças nucleares são menos atraentes, uma indicação de até que ponto a força nuclear pode depender da combinação particular de nêutrons e prótons. O conceito de meia-vida é aplicável a outras partículas subatômicas, como será discutido em Física de Partículas. Também é aplicável ao decaimento de estados excitados em átomos e núcleos. A equação a seguir fornece a relação quantitativa entre o número original de núcleos presentes no tempo zero (N_0\) e o número (\(N\)) em um momento posterior\(t\).

\[N = N_0e^{-\lambda t},\]onde\(e = 2.71828 . . .\) está a base do logaritmo natural e\(\lambda\) é a constante de decaimento do nuclídeo. Quanto menor a meia-vida, maior é o valor de\(\lambda\) e mais rápido o exponencial\(e^{\lambda t}\) diminui com o tempo. A relação entre a constante de decaimento\(\lambda\) e a meia-vida\(t_{1/2}\) é

\[\lambda = \dfrac{ln(2)}{t_{1/2}} \approx \dfrac{0.693}{t_{1/2}}.\]

Para ver como o número de núcleos diminui para a metade de seu valor original em uma meia-vida, deixe entrar\(t = t_{1/2}\) o exponencial na equação\(N = N_0e^{-\lambda t}\). Isso dá

\[N = N_0e^{-\lambda t} = N_0e^{-0.693} = 0.500 N_0.\]Para números integrais de meias-vidas, você pode simplesmente dividir o número original por 2 repetidamente, em vez de usar a relação exponencial. Por exemplo, se dez meias-vidas passaram, dividimos\(N\) por 2 dez vezes. Isso o reduz para\(N/1024\). Por um tempo arbitrário, não apenas um múltiplo da meia-vida, a relação exponencial deve ser usada.

A datação radioativa é um uso inteligente da radioatividade natural. Sua aplicação mais famosa é a datação por carbono 14. O carbono-14 tem meia-vida de 5730 anos e é produzido em uma reação nuclear induzida quando neutrinos solares\(^{14}N\) atingem a atmosfera. O carbono radioativo tem a mesma química do carbono estável e, portanto, se mistura à ecosfera, onde é consumido e se torna parte de todos os organismos vivos. O carbono-14 tem uma abundância de 1,3 partes por trilhão de carbono normal. Assim, se você souber o número de núcleos de carbono em um objeto (talvez determinado pela massa e pelo número de Avogadro), multiplique esse número por\(1.3 \times 10^{-12}\) para encontrar o número de\(^{14}C\) núcleos no objeto. Quando um organismo morre, a troca de carbono com o meio ambiente cessa e não\(^{14}C\) é reabastecido à medida que se decompõe. Ao comparar a abundância de\(^{14}C\) em um artefato, como embalagens de múmias, com a abundância normal em tecidos vivos, é possível determinar a idade do artefato (ou o tempo desde a morte). A datação por carbono-14 pode ser usada para tecidos biológicos de até 50 ou 60 mil anos, mas é mais precisa para amostras mais jovens, já que a abundância de\(^{14}C\) núcleos nelas é maior. Materiais biológicos muito antigos não contêm\(^{14}C\) absolutamente nada. Há casos em que a data de um artefato pode ser determinada por outros meios, como conhecimento histórico ou contagem de anéis de árvores. Essas referências cruzadas confirmaram a validade da datação por carbono 14 e também nos permitiram calibrar a técnica. A datação por carbono 14 revolucionou partes da arqueologia e é de tal importância que ganhou o Prêmio Nobel de Química de 1960 para seu desenvolvedor, o químico americano Willard Libby (1908—1980).

Um dos casos mais famosos de datação por carbono 14 envolve o Sudário de Turim, um longo pedaço de tecido que supostamente é a mortalha de Jesus (Figura\(\PageIndex{2}\)). Essa relíquia foi exibida pela primeira vez em Turim em 1354 e foi denunciada como uma fraude na época por um bispo francês. Sua notável impressão negativa de um corpo aparentemente crucificado lembra a imagem então aceita de Jesus e, portanto, a mortalha nunca foi completamente ignorada e permaneceu controversa ao longo dos séculos. A datação por carbono 14 não foi realizada na mortalha até 1988, quando o processo foi refinado até o ponto em que apenas uma pequena quantidade de material precisava ser destruída. As amostras foram testadas em três laboratórios independentes, cada um recebendo quatro pedaços de tecido, com apenas um pedaço não identificado da mortalha, para evitar preconceitos. Todos os três laboratórios descobriram que amostras da mortalha contêm 92% das\(^{14}C\) encontradas em tecidos vivos, permitindo que a mortalha seja datada (exemplo\(\PageIndex{1}\)).

Figura\(\PageIndex{2}\): Parte do Sudário de Turim, que mostra uma notável semelhança negativa de Jesus, com evidências de ferimentos de crucificação. A mortalha surgiu pela primeira vez no século XIV e só recentemente foi datada com carbono 14. Não foi determinado como a imagem foi colocada no material. (crédito: Butko, Wikimedia Commons)

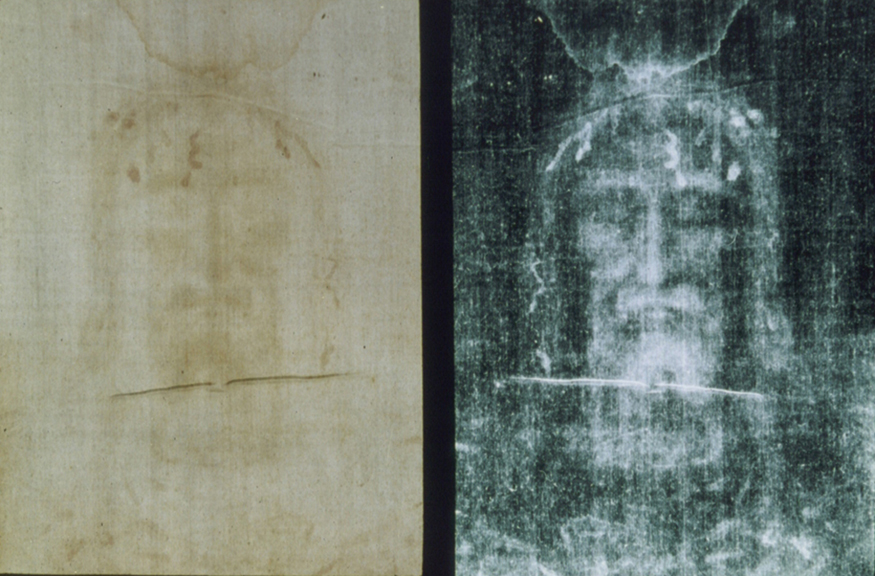
Exemplo\(\PageIndex{1}\): How Old Is the Shroud of Turin?

Calcule a idade do Sudário de Turim, dado que a quantidade\(^{14}C\) encontrada nele é 92% da encontrada nos tecidos vivos.

Estratégia

Saber que 92% dos\(^{14}C\) restos mortais significa isso\(N/N_0 = 0.92\). Portanto, a equação\(N = N_0e^{-\lambda t}\) pode ser usada para encontrar\(\lambda t\). Também sabemos que a meia-vida de\(^{14}C\) é de 5730 y e, assim, uma vez\(\lambda t\) conhecida, podemos usar a equação\(\lambda = \frac{0.693}{t_{1/2}}\) para encontrar\(\lambda\) e depois encontrar\(t\) conforme solicitado. Aqui, postulamos que a diminuição\(^{14}C\) do se deve exclusivamente à decadência nuclear.

Solução

Resolver a equação\(N = N_0e^{-\lambda t}\) para N/N_0\) dá

\[\dfrac{N}{N_0} = e^{-\lambda t}.\]

Assim,

\[0.92 = e^{-\lambda t}\]

Tomando o logaritmo natural de ambos os lados da equação resulta

\[ln \, 0.92 = - \lambda t\]

para que

\[-0.0834 = -\lambda t.\]

Reorganizar para isolar\(t\) dá

\[t = \dfrac{0.0834}{\lambda}.\]

Agora, a equação\(\lambda = \frac{0.693}{t_{1/2}}\) pode ser usada\(|lambda\) para encontrar\(^{14}C\). Resolver\(\lambda\) e substituir a meia-vida conhecida dá

\[\lambda = \dfrac{0.693}{t_{1/2}} = \dfrac{0.693}{5730 \, y}.\]

Nós inserimos esse valor na equação anterior para encontrar\(t\).

\[t = \dfrac{0.0834}{\frac{0.693}{5730 \, y}} = 690 \, y.\]

Discussão

Isso data o material na mortalha de 1988-690 = 1300 d.C. Nosso cálculo é preciso apenas para dois dígitos, de modo que o ano é arredondado para 1300. Os valores obtidos nos três laboratórios independentes deram uma data média ponderada de a.d\(1320 \pm 60\). A incerteza é típica da datação por carbono 14 e se deve à pequena quantidade de\(^{14}C\) tecidos vivos, à quantidade de material disponível e às incertezas experimentais (reduzidas por três medições independentes). É significativo que a data do sudário seja consistente com o primeiro registro de sua existência e inconsistente com o período em que Jesus viveu.

Existem outras formas de datação radioativa. Rochas, por exemplo, às vezes podem ser datadas com base na decadência de\(^{238}U\). A série de decaimento\(^{238}U\) termina com\(^{206}Pb\), de modo que a proporção desses nuclídeos em uma rocha é uma indicação de quanto tempo se passou desde que a rocha se solidificou. A composição original da rocha, como a ausência de chumbo, deve ser conhecida com alguma confiança. No entanto, como acontece com a datação por carbono-14, a técnica pode ser verificada por um corpo consistente de conhecimento. Uma vez que\(^{238}U\) tem meia-vida de\(4.5 \times 10^9\) y, é útil para datar apenas materiais muito antigos, mostrando, por exemplo, que as rochas mais antigas da Terra se solidificaram há cerca de\(3.5 \times 10^9\) anos.

Atividade, a taxa de decaimento

O que queremos dizer quando dizemos que uma fonte é altamente radioativa? Geralmente, isso significa que o número de decaimentos por unidade de tempo é muito alto. Definimos atividade\(R\) como sendo a taxa de decaimento expressa em decaimentos por unidade de tempo. Em forma de equação, isso é

\[R = \dfrac{\Delta N}{\Delta t}\]onde\(\Delta N\) está o número de decaimentos que ocorrem com o tempo\(\Delta t\). A unidade SI para atividade é de um decaimento por segundo e recebe o nome de becquerel (Bq) em homenagem ao descobridor da radioatividade. Ou seja,

\[1 \, Bq = 1 \, decay/s.\]

\(R\)A atividade geralmente é expressa em outras unidades, como decaimentos por minuto ou decaimentos por ano. Uma das unidades de atividade mais comuns é a curie (Ci), definida como sendo a atividade de 1 g de\(^{226}Ra\), em homenagem ao trabalho de Marie Curie com o rádio. A definição de curie é

\[1 \, Ci = 3.70 \times 10^{10} \, Bq,\]ou\(3.70 \times 10^{10}\) decai por segundo. Um curie é uma grande unidade de atividade, enquanto um becquerel é uma unidade relativamente pequena.\ (1\, MBq = 100\, microcuries\, (\ muCi). Em países como Austrália e Nova Zelândia, que aderem mais às unidades SI, a maioria das fontes radioativas, como as usadas em diagnósticos médicos ou em laboratórios de física, são rotuladas em Bq ou megabecquerel (MBq).

Intuitivamente, você esperaria que a atividade de uma fonte dependesse de duas coisas: a quantidade da substância radioativa presente e sua meia-vida. Quanto maior o número de núcleos radioativos presentes na amostra, mais decairá por unidade de tempo. Quanto menor a meia-vida, mais decaimentos por unidade de tempo, para um determinado número de núcleos. Portanto, a atividade\(R\) deve ser proporcional ao número de núcleos radioativos,\(N\), e inversamente proporcional à sua meia-vida,\(t_{1/2}\). Na verdade, sua intuição está correta. Pode-se mostrar que a atividade de uma fonte é

\[R = \dfrac{0.693 \, N}{t_{1/2}}\]

onde\(N\) está o número de núcleos radioativos presentes, com meia-vida\(t_{1/2}\). Essa relação é útil em vários cálculos, como ilustram os próximos dois exemplos.

Exemplo\(\PageIndex{2}\): How Great is the \(^{14}C\) Activity in Living Tissue?

Calcule a atividade devida a\(^{14}C\) 1,00 kg de carbono encontrado em um organismo vivo. Expresse a atividade em unidades de Bq e Ci.

Estratégia

Para encontrar a atividade\(R\) usando a equação\(R = \frac{0.693 N}{t_{1/2}}\), devemos saber\(N\)\(t_{1/2}\) e. A meia-vida de\(^{14}C\) pode ser encontrada no Apêndice B, e foi declarada acima como 5730 y. Para descobrir\(N\), primeiro encontramos o número de\(^{12}C\) núcleos em 1,00 kg de carbono usando o conceito de toupeira. Conforme indicado, multiplicamos por\(1.3 \times 10^{-12}\) (a abundância de\(^{14}C\) em uma amostra de carbono de um organismo vivo) para obter o número de\(^{14}C\) núcleos em um organismo vivo.

Solução

Um mol de carbono tem uma massa de 12,0 g, já que é quase puro\(^{12}C\). (Uma toupeira tem uma massa em gramas igual em magnitude à\(A\) encontrada na tabela periódica.) Assim, o número de núcleos de carbono em um quilograma é

\[N(^{12}C = \dfrac{6.02 \times 10^{23} \, mol^{-1}}{12.0 \, g/mol} \times (1000 \, g) = 5.02 \times 10^{25}. \nonumber\]

Portanto, o número de\(^{14}C\) núcleos em 1 kg de carbono é

\[N(^{14}C) = (5.02 \times 10^{25})(1.3 \times 10^{-12}) = 6.52 \times 10^{13}.\nonumber\]

Agora, a atividade\(R\) é encontrada usando a equação\(R = \frac{0.693 N}{t_{1/2}}\). A inserção de valores conhecidos fornece

\[R = \dfrac{0.693(6.52 \times 10^{13})}{5730 \, y} = 7.89 \times 10^9 \, y^{-1},\nonumber\]

ou\(7.89 \times 10^9\) decai por ano. Para converter isso na unidade Bq, simplesmente convertemos anos em segundos. Assim,

\[R = (7.89 \times 10^9 \, y^{-1}) \dfrac{1.00 \, y}{3.16 \times 10^7 \, s} = 250 \, Bq, \nonumber\]

ou 250 decaimentos por segundo. Para expressar\(R\) em curies, usamos a definição de curie,

\[R = \dfrac{250 \, Bq}{3.7 \times 10^{10} \, Bq/Ci} = 6.76 \times 10^{-9} \, Ci.\nonumber\]

Assim,

\[R = 6.76 \, nCi.\nonumber\]

Discussão

Nossos próprios corpos contêm quilos de carbono, e é intrigante pensar que há centenas de\(^{14}C\) decaimentos por segundo ocorrendo em nós. O carbono-14 e outras substâncias radioativas que ocorrem naturalmente em nossos corpos contribuem para a radiação de fundo que recebemos. O pequeno número de decaimentos por segundo encontrado para um quilograma de carbono neste exemplo dá uma ideia de como é difícil detectá-lo\(^{14}C\) em uma pequena amostra de material. Se houver 250 decaimentos por segundo em um quilograma, haverá 0,25 decaimentos por segundo em um grama de carbono no tecido vivo. Para observar isso, você deve ser capaz de distinguir os decaimentos de outras formas de radiação, a fim de reduzir o ruído de fundo. Isso se torna mais difícil com uma amostra de tecido antiga, pois contém menos\(^{14}C\), e para amostras com mais de 50 mil anos, é impossível.

A radioatividade produzida pelo homem (ou artificial) é produzida há décadas e tem muitos usos. Alguns deles incluem terapia médica para câncer, imagens e diagnósticos médicos e preservação de alimentos por irradiação. Muitas aplicações, bem como os efeitos biológicos da radiação, são explorados em Aplicações Médicas da Física Nuclear, mas está claro que a radiação é perigosa. Existem vários exemplos trágicos disso, um dos mais desastrosos é o colapso e o incêndio no complexo do reator de Chernobyl, na Ucrânia (Figura\(\PageIndex{3}\)). Vários isótopos radioativos foram liberados em grandes quantidades, contaminando muitos milhares de quilômetros quadrados e afetando diretamente centenas de milhares de pessoas. Os lançamentos mais significativos foram de\(^{131}I\)\(^{90}Sr\)\(^{137}Cs\),\(^{239}Pu\),\(^{238}U\),,\(^{235}U\) e. As estimativas são de que a quantidade total de radiação liberada foi de cerca de 100 milhões de curies.

Aplicações humanas e médicas

Figura\(\PageIndex{3}\): O reator de Chernobyl. Mais de 100 pessoas morreram logo após seu colapso, e haverá milhares de mortes por câncer induzido por radiação no futuro. Embora o acidente tenha sido devido a uma série de erros humanos, os esforços de limpeza foram heróicos. A maioria das mortes imediatas foram bombeiros e pessoal do reator. (crédito: Elena Filatova)

Exemplo\(\PageIndex{3}\): What Mass of \(^{137}Cs\) Escaped Chernobyl?

Estima-se que o desastre de Chernobyl tenha liberado 6,0 mCi de\(^{137}Cs\) no meio ambiente. Calcule a massa\(^{137}Cs\) liberada.

Estratégia

Podemos calcular a massa liberada usando o número de Avogadro e o conceito de toupeira se pudermos primeiro encontrar o número de núcleos\(N\) liberados. Como a atividade\(R\) é dada e a meia-vida de\(^{137}Cs\) é encontrada no Apêndice B em 30,2 y, podemos usar a equação\(N = \frac{0.693N}{t_{1/2}}\) para encontrar\(N\).

Solução

Resolvendo a equação\(N = \frac{0.693N}{t_{1/2}}\) para\(N\) dados

\[N = \dfrac{Rt_{1/2}}{0.693}.\]

Ao inserir os valores fornecidos, obtém-se

\[N = \dfrac{(6.0 \, MCo)(30.2 \, y)}{0.693}.\]

Convertendo curies em becquerels e anos em segundos, obtemos

\[N = \dfrac{(6.0 \times 10^6 \, Ci)(3.7 \times 10^{10} \, Bq/Ci)(39.2 \, y)(3.16 \times 10^7 \, s/y)}{0.693} = 3.1 \times 10^{26}.\]

Uma toupeira de um nuclídeo\(^AX\) tem uma massa de\(A\) gramas, de modo que uma mol de\(^{137}Cs\) tem uma massa de 137 g. Uma toupeira tem\(6.02 \times 10^{23}\) núcleos. Assim, a massa de\(^{137}Cs\) liberados foi

\[m = \left(\dfrac{137 \, g}{6.02 \times 10^{23}} \right)(3.1 \times 10^{26}) = 70 \times 10^3 \, g = 70 \, kg.\]

Discussão

Embora 70 kg de material possam não ser uma massa muito grande em comparação com a quantidade de combustível em uma usina, ele é extremamente radioativo, pois tem meia-vida de apenas 30 anos. Seis megacurias (6,0 mCi) são uma quantidade extraordinária de atividade, mas são apenas uma fração do que é produzido em reatores nucleares. Quantidades semelhantes dos outros isótopos também foram liberadas em Chernobyl. Embora as chances de tal desastre possam ter parecido pequenas, as consequências foram extremamente graves, exigindo maior cautela do que a usada. Mais informações serão ditas sobre o projeto seguro de reatores no próximo capítulo, mas deve-se observar que os reatores ocidentais têm um design fundamentalmente mais seguro.

A atividade\(R\) diminui com o tempo, chegando à metade de seu valor original em uma meia-vida, depois para um quarto de seu valor original na próxima meia-vida, e assim por diante. Desde então\(R = \frac{0.693N}{t_{1/2}}\), a atividade diminui à medida que o número de núcleos radioativos diminui. A equação para\(R\) em função do tempo é encontrada combinando as equações\(N = N_0e^{-\lambda t}\) e\(R = \frac{0.693N}{t_{1/2}}\), produzindo

\[R = R_0e^{-\lambda t},\]

onde\(R_0\) está a atividade\(t = 0\). Esta equação mostra o decaimento exponencial dos núcleos radioativos. Por exemplo, se uma fonte originalmente tem uma atividade de 1,00 mCi, ela diminui para 0,500 mCi em uma meia-vida, para 0,250 mCi em duas meias-vidas, para 0,125 mCi em três meias-vidas e assim por diante. Para épocas diferentes de meias-vidas inteiras, a equação\(R = R_0 e^{-\lambda t}\) deve ser usada para encontrar\(R\).

EXPLORAÇÕES DE PHET: ALPHA DECAY

Veja as partículas alfa escaparem de um núcleo de polônio, causando decaimento alfa radioativo. Veja como tempos de decaimento aleatórios se relacionam com a meia-vida.

Resumo

• Meia-vida\(t_{1/2}\) é o momento em que há 50% de chance de um núcleo se decompor. O número de\(N\) núcleos em função do tempo é\[N = N_0e^{-\lambda t},\] onde\(N_0\) está o número presente\(t = 0\), e\(\lambda\) é a constante de decaimento, relacionada à meia-vida por\[\lambda = \dfrac{0.693}{t_{1/2}}.\]
• Uma das aplicações do decaimento radioativo é a datação radioativa, em que a idade de um material é determinada pela quantidade de decaimento radioativo que ocorre. A taxa de decaimento é chamada de atividade\(R\):\[R = \dfrac{\Delta N}{\Delta t}.\]
• A unidade SI para\(R\) é o becquerel (Bq), definido por\[1 \, Bq = 1 \, decay/s.\]
• \(R\)também é expresso em termos de curies (Ci), onde\[1 \, Ci = 3.70 \times 10^{10} \, Bq.\]
• A atividade\(R\) de uma fonte está relacionada com\(N\) e\(t_{1/2}\) por\[R = \dfrac{0.693N}{t_{1/2}}.\]
• Como\(N\) tem um comportamento exponencial como na equação\(N = N_0e^{-\lambda t}\), a atividade também tem um comportamento exponencial, dado por\[R = R_0e^{-\lambda t},\] onde\(R-0\) está a atividade\(t = 0\).

Glossário

becquerel

Unidade SI para taxa de decaimento de um material radioativo

meia-vida

o momento em que há 50% de chance de um núcleo se decompor

datação radioativa

uma aplicação de decaimento radioativo em que a idade de um material é determinada pela quantidade de radioatividade de um tipo específico que ocorre

constante de decaimento

quantidade que é inversamente proporcional à meia-vida e que é usada na equação do número de núcleos em função do tempo

datação por carbono-14

uma técnica de datação radioativa baseada na radioatividade do carbono-14

atividade

a taxa de decaimento de nuclídeos radioativos

taxa de decaimento

o número de eventos radioativos por unidade de tempo

curie

a atividade de 1g de\(^{226}Ra\), igual a\(3.70 \times 10^{10} \, Bq\)