31.6: Energia vinculativa

Last updated
Save as PDF

Page ID: 194598

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

objetivos de aprendizagem

Ao final desta seção, você poderá:

Defina e discuta a energia vinculativa.
Calcule a energia de ligação por núcleo de uma partícula.

Quanto mais estreitamente ligado for um sistema, mais fortes serão as forças que o mantêm unido e maior a energia necessária para separá-lo. Portanto, podemos aprender sobre as forças nucleares examinando o quão estreitamente ligados os núcleos estão. Definimos a energia de ligação (BE) de um núcleo como a energia necessária para desmontá-lo completamente em prótons e nêutrons separados. Podemos determinar o BE de um núcleo a partir de sua massa restante. Os dois estão conectados por meio do famoso relacionamento de Einstein\(E = (\Delta m)c^2\).

Um sistema ligado tem uma massa menor do que seus constituintes separados; quanto mais fortemente os nucleons estão unidos, menor a massa do núcleo.

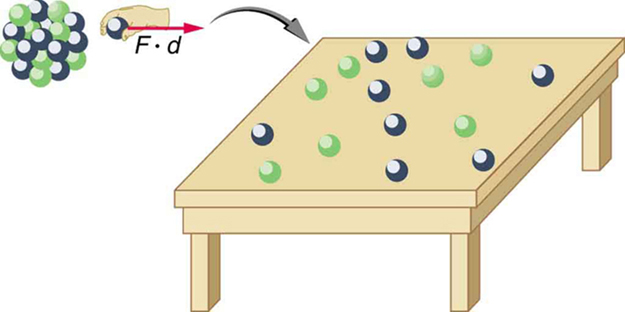
A imagem mostra alguns prótons e nêutrons esféricos retirados de um núcleo. O trabalho realizado para separá-los é uma energia vinculativa. — Figura\(\PageIndex{1}\): O trabalho realizado para separar um núcleo em seus prótons e nêutrons constituintes aumenta a massa do sistema. O trabalho para desmontar o núcleo é igual à sua energia de ligação BE. Um sistema ligado tem menos massa do que a soma de suas partes, especialmente perceptível nos núcleos, onde as forças e energias são muito grandes.

Imagine separar um nuclídeo conforme ilustrado na Figura\(\PageIndex{1}\). O trabalho realizado para superar as forças nucleares que mantêm o núcleo unido coloca energia no sistema. Por definição, a entrada de energia é igual à energia de ligação BE. As peças ficam em repouso quando separadas e, portanto, a energia colocada nelas aumenta sua massa total de repouso em comparação com o que era quando foram coladas como um núcleo. Esse aumento de massa é, portanto,\(\Delta m = BE/c^2\) essa diferença de massa é conhecida como defeito de massa. Isso implica que a massa do núcleo é menor que a soma das massas de seus prótons e nêutrons constituintes. Um nuclídeo\(^AX\) tem\(Z\) prótons e\(N\) nêutrons, então a diferença na massa é

\[ \Delta m = (Zm_p + Nm_n) - M_{tot}.\]Assim,

\[BE = (∆m)c^2 = [(Zm_p + Nm_n) − m_{tot}]c^2.\]

onde\(m_{tot}\) está a massa do nuclídeo\(^AX\),\(m_p\) é a massa de um próton e\(m_n\) é a massa de um nêutron. Tradicionalmente, lidamos com massas de átomos neutros. Para colocar as massas atômicas na última equação, primeiro adicionamos\(Z\) elétrons aos\(m_{tot}\) quais dá\(m(^AX)\) a massa atômica do nuclídeo. Em seguida, adicionamos\(Z\) elétrons aos\(Z\) prótons, o que dá\(Zm(^1H)\), ou\(Z\) vezes, a massa de um átomo de hidrogênio. Assim, a energia de ligação de um\(^AX\) nuclídeo é

\[BE = [(Z_m(^1H) + Nm_n) - m(^AX)]c^2 \label{BE}\]

As massas atômicas podem ser encontradas no Apêndice A, mais convenientemente expressas em unidades de massa atômica unificadas\((1 \, u = 931.5 \, MeV/c^2)\) u. O BE é, portanto, calculado a partir de massas atômicas conhecidas.

A decadência nuclear ajuda a explicar o interior quente da Terra

Um quebra-cabeça criado pela datação radioativa de rochas é resolvido pelo aquecimento radioativo do interior da Terra. Essa história intrigante é outro exemplo de como a física de pequena escala pode explicar fenômenos de grande escala.

A datação radioativa desempenha um papel na determinação da idade aproximada da Terra. As rochas mais antigas da Terra se solidificaram\(3.5 \times 10^9\) há cerca de anos - um número determinado pela datação por urânio-238. Essas rochas só poderiam ter se solidificado depois que a superfície da Terra tivesse esfriado o suficiente. A temperatura da Terra na formação pode ser estimada com base na energia potencial gravitacional do conjunto de peças que estão sendo convertidas em energia térmica. Usando os conceitos de transferência de calor discutidos em Termodinâmica, é possível calcular quanto tempo levaria para a superfície esfriar até as temperaturas de formação rochosa. O resultado é de cerca de\(10^9\) anos. As primeiras rochas formadas são sólidas há\(3.5 \times 10^9\) anos, de modo que a idade da Terra é de aproximadamente\(4.5 \times 10^9\) anos. Há um grande conjunto de outros tipos de evidências (tanto as características ligadas à Terra quanto as do sistema solar são usadas) que apóiam essa era. O quebra-cabeça é que, dada sua idade e temperatura inicial, o centro da Terra deveria estar muito mais frio do que é hoje (Figura\(\PageIndex{2}\)).

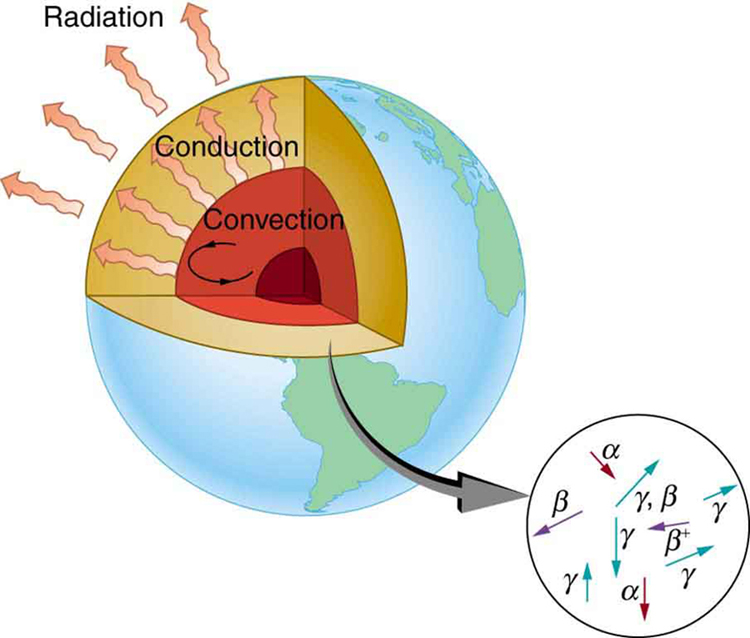
A figura mostra que o centro da Terra esfria por três métodos de transferência de calor. A transferência de calor por convecção na região central, em seguida, a transferência de calor por condução move a energia térmica para a superfície e, finalmente, a transferência de calor por radiação da superfície para o espaço. — Figura\(\PageIndex{2}\): O centro da Terra esfria por métodos conhecidos de transferência de calor. A convecção nas regiões líquidas e a condução movem a energia térmica para a superfície, onde ela irradia para o espaço frio e escuro. Dada a idade da Terra e sua temperatura inicial, ela já deveria ter esfriado a uma temperatura mais baixa. A explosão mostra que a decadência nuclear libera energia no interior da Terra. Essa energia retardou o processo de resfriamento e é responsável pela fusão do interior.

Sabemos pelas ondas sísmicas produzidas por terremotos que partes do interior da Terra são líquidas. Ondas de cisalhamento ou transversais não podem viajar através de um líquido e não são transmitidas pelo núcleo da Terra. No entanto, ondas de compressão ou longitudinais podem passar por um líquido e atravessar o núcleo. A partir dessas informações, a temperatura do interior pode ser estimada. Conforme percebido, o interior deveria ter esfriado mais em relação à temperatura inicial nos\(4.5 \times 10^9\) anos desde sua formação. Na verdade, não deveria ter demorado mais do que cerca de\(10^9\) anos para esfriar até a temperatura atual. O que o mantém quente? A resposta parece ser o decaimento radioativo de elementos primordiais que faziam parte do material que formou a Terra (veja a explosão na Figura\(\PageIndex{2}\)).

Nuclídeos como\(^{238}U\) e\(^{40}K\) têm meia-vida semelhante ou superior à idade da Terra, e sua decadência ainda contribui com energia para o interior. Alguns dos nuclídeos radioativos primordiais têm produtos de decaimento instáveis que também liberam energia -\(\ce{^{238}U}\) tem uma longa cadeia de decaimento destes. Além disso, havia mais desses nuclídeos radioativos primordiais no início da vida da Terra e, portanto, a atividade e a energia contribuídas eram maiores na época (talvez em uma ordem de magnitude). A quantidade de energia criada por esses decaimentos por metro cúbico é muito pequena. No entanto, como um grande volume de material está bem abaixo da superfície, essa quantidade relativamente pequena de energia não pode escapar rapidamente. A energia produzida perto da superfície tem muito menos distância a percorrer para escapar e tem um efeito insignificante nas temperaturas da superfície.

Um efeito final dessa radiação aprisionada merece menção. O decaimento alfa produz núcleos de hélio, que formam átomos de hélio quando são parados e capturam elétrons. A maior parte do hélio na Terra é obtida de poços e é produzida dessa maneira. Qualquer hélio na atmosfera escapará em tempos geologicamente curtos devido à sua alta velocidade térmica.

Quais padrões e insights são obtidos com um exame da energia de ligação de vários nuclídeos? Primeiro, descobrimos que BE é aproximadamente proporcional ao número de nucleons\(A\) em qualquer núcleo. Cerca de duas vezes mais energia é necessária para separar um núcleo,\(^{24}Mg\) em comparação com a separação\(^{12}C\), por exemplo. Para nos ajudar a analisar outros efeitos, dividimos BE por\(A\) e consideramos a energia de ligação por núcleo,\(BE/A\). O gráfico da\(BE/A\) Figura\(\PageIndex{3}\) revela alguns aspectos muito interessantes dos núcleos. Vemos que a energia de ligação por núcleo é em média de cerca de 8 MeV, mas é menor tanto para os núcleos mais leves quanto para os mais pesados. Essa tendência geral, na qual núcleos\(A\) iguais a cerca de 60 têm os maiores\(BE/A\) e, portanto, os mais estreitamente ligados, deve-se às características combinadas das forças nucleares atraentes e da força repulsiva de Coulomb.

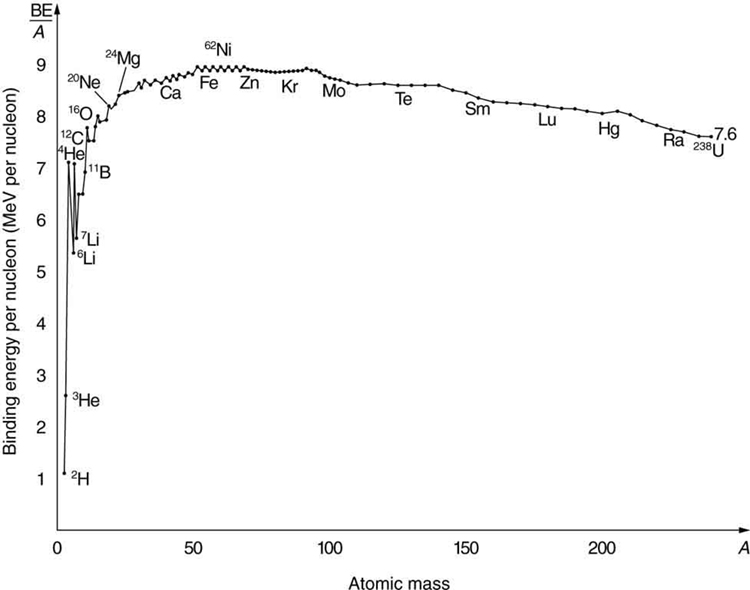
A figura mostra um gráfico da energia de ligação por núcleo versus a massa atômica para diferentes elementos. A partir do gráfico, pode-se observar que elementos com massa atômica próxima a sessenta têm maior energia de ligação por núcleo. — Figura\(\PageIndex{3}\): Um gráfico da energia média de ligação por núcleo,\(BE/A\), para núcleos estáveis. Os núcleos mais estreitamente ligados são aqueles com\(A\) cerca de 60, onde a força nuclear atraente tem seu maior efeito. Em níveis mais\(A\) altos, a repulsão de Coulomb reduz progressivamente a energia de ligação por núcleo, porque a força nuclear é de curto alcance. Os picos na curva são nuclídeos muito estreitamente ligados e indicam o fechamento de conchas.

É especialmente importante observar duas coisas: a força nuclear forte é cerca de 100 vezes mais forte que a força de Coulomb, e as forças nucleares têm menor alcance em comparação com a força de Coulomb. Assim, para núcleos de baixa massa, a atração nuclear domina e cada núcleo adicionado forma ligações com todos os outros, fazendo com que núcleos progressivamente mais pesados tenham valores progressivamente maiores de\(BE/A\). Isso continua até\(A \approx 60\), correspondendo aproximadamente ao número de massa de ferro. Além disso, novos nucleons adicionados a um núcleo estarão muito distantes de alguns outros para sentir sua atração nuclear. Os prótons adicionados, no entanto, sentem a repulsão de todos os outros prótons, já que a força de Coulomb tem maior alcance. A repulsão de Coulomb cresce para núcleos progressivamente mais pesados, mas a atração nuclear permanece praticamente a mesma e, portanto,\(BE/A\) se torna menor. É por isso que núcleos estáveis mais pesados do que\(A \approx 40\) têm mais nêutrons do que prótons. A repulsão de Coulomb é reduzida por ter mais nêutrons para manter os prótons mais afastados (Figura\(\PageIndex{4}\)).

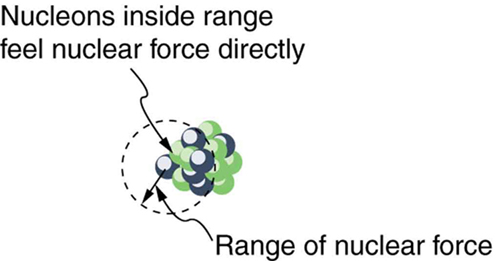
A imagem mostra vários núcleons esféricos dentro de um núcleo. É mostrado um caminho circular tracejado que mostra o alcance da força nuclear e os nucleons dentro dessa faixa sentem a força nuclear diretamente. — Figura\(\PageIndex{4}\): A força nuclear é atraente e mais forte do que a força de Coulomb, mas é de curto alcance. Em núcleos de baixa massa, cada núcleo sente a atração nuclear de todos os outros. Em núcleos maiores, o alcance da força nuclear, mostrado para um único núcleo, é menor que o tamanho do núcleo, mas a repulsão de Coulomb de todos os prótons atinge todos os outros. Se o núcleo for grande o suficiente, a repulsão de Coulomb pode aumentar para superar a atração nuclear.

Existem alguns picos visíveis no\(BE/A\) gráfico, que representam núcleos particularmente estreitamente ligados. Esses picos revelam mais detalhes das forças nucleares, como a confirmação de que núcleos de casca fechada (aqueles com números mágicos de prótons ou nêutrons ou ambos) estão mais estreitamente ligados. Os picos também indicam que alguns núcleos com números pares para\(Z\)\(N\) e com\(Z = N\) estão excepcionalmente estreitamente ligados. Essa descoberta pode ser correlacionada com algumas das abundâncias cósmicas dos elementos. Os elementos mais comuns no universo, conforme determinado pelas observações dos espectros atômicos do espaço sideral, são o hidrogênio, seguido por\(^4He\) quantidades muito menores de\(^{12}C\) e outros elementos. Deve-se notar que os elementos mais pesados são criados em explosões de supernovas, enquanto os mais leves são produzidos pela fusão nuclear durante os ciclos normais de vida das estrelas, como será discutido nos capítulos subsequentes. Os elementos mais comuns têm os núcleos mais estreitamente ligados. Também não é por acaso que um dos núcleos de luz mais estreitamente ligados é\(^4He\) emitido em\(\alpha\) decomposição.

Exemplo\(\PageIndex{1}\): What Is \(BE/A\) for an Alpha Particle?

Calcule a energia de ligação por núcleo\(^4He\) da\(\alpha\) partícula.

Estratégia

Para encontrar, primeiro\(BE/A\) encontramos BE usando a equação\(BE = [(Z_m(^1H) + Nm_n) - m(^AX)]c^2\) e depois dividimos por\(A\). Isso é simples, uma vez que pesquisamos as massas atômicas apropriadas no Apêndice A.

Solução

A energia de ligação para um núcleo é dada pela equação

\[BE = [(Z_m(^1H) + Nm_n) - m(^AX)]c^2 \nonumber\]

\(^4He\)Pois, temos\ (Z = N = 2; portanto,

\[BE = [(2m(^1H) + 2Nm_n) - m(^4He)]c^2. \nonumber\]

O Apêndice A fornece essas massas como\(m(^4He) = 4.002602 \, u\). \(m(^1H) = 1.007825 \, u\),\(m_n = 1.008665 \, u\) e. Assim

\[BE = (0.030378 \, u)c^2. \nonumber\]

Observando isso\(1 \, u = 931.5 \, MeV/c^2\), encontramos

\[BE = (0.030378)(931.5 \, MeV/c^2)c^2 = 28.3 \, MeV. \nonumber\]

Desde então\(A = 4\), vemos que esse número\(BE/A\) é dividido por 4, ou

\[BE/A = 7.07 \, MeV/nucleon. \nonumber\]

Discussão

Esta é uma grande energia de ligação por núcleo em comparação com as de outros núcleos de baixa massa, que têm\(BE/A \approx 3 \, MeV/nucleon\). Isso indica que\(^4He\) está estreitamente vinculado em comparação com seus vizinhos no gráfico dos nuclídeos. Você pode ver o pico representando esse valor de\(BE/A\) for\(^4He\) no gráfico da Figura. É por isso que\(^4He\) é estável. Como\(^4He\) está fortemente ligado, tem menos massa do que outros\(A = 4\) núcleos e, portanto, não pode se decompor espontaneamente neles. A grande energia de ligação também ajuda a explicar por que alguns núcleos se decompõem. Uma massa menor nos produtos de decaimento pode significar liberação de energia, e esses decaimentos podem ser espontâneos. Além disso, pode acontecer que dois prótons e dois nêutrons em um núcleo possam se encontrar aleatoriamente juntos, experimentar a força nuclear excepcionalmente grande que liga essa combinação e atuar como uma\(^4He\) unidade dentro do núcleo, pelo menos por um tempo. Em alguns casos,\(^4He\) as fugas e a\(\alpha\) decadência ocorreram.

Há mais a ser aprendido com as energias de ligação nuclear. A tendência geral em\(BE/A\) é fundamental para a produção de energia nas estrelas e para as fontes de energia de fusão e fissão na Terra, por exemplo. Essa é uma das aplicações da física nuclear abordadas em Aplicações Médicas da Física Nuclear. A abundância de elementos na Terra, nas estrelas e no universo como um todo está relacionada à energia de ligação dos núcleos e tem implicações para a expansão contínua do universo.

Estratégias de resolução de problemas: para cálculos de reação, energia de ligação e atividade

Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas). Isso permitirá que você decida se a energia de um decaimento ou reação nuclear está envolvida, por exemplo, ou se o problema está relacionado principalmente à atividade (taxa de decaimento).
Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos).
Para problemas de reação e energia de ligação, usamos massas atômicas em vez de nucleares. Como as massas de átomos neutros são usadas, você deve contar o número de elétrons envolvidos. Se eles não se equilibrarem (como em\(\beta^+\) decaimento), um ajuste de energia de 0,511 MeV por elétron deve ser feito. Observe também que as massas atômicas podem não ser dadas em um problema; elas podem ser encontradas em tabelas.
Para problemas envolvendo atividade, a relação da atividade com a meia-vida e o número de núcleos dados na equação\(R = \frac{0.693N}{t_{1/2}}\) podem ser muito úteis. Devido ao fato de o número de núcleos estar envolvido, você também precisará estar familiarizado com as toupeiras e o número de Avogadro.
Execute o cálculo desejado; acompanhe cuidadosamente os sinais de mais e menos, bem como as potências de 10.
Verifique a resposta para ver se é razoável: Faz sentido? Compare seus resultados com exemplos práticos e outras informações no texto. (Seguir os conselhos da Etapa 5 também o ajudará a ter certeza do resultado.) Você deve entender o problema conceitualmente para poder determinar se o resultado numérico é razoável.

EXPLORAÇÕES DE PHET: FISSÃO NUCLEAR

Baixe a simulação PhET e inicie uma reação em cadeia, ou introduza isótopos não radioativos para evitar uma. Controle a produção de energia em um reator nuclear!

Resumo

A energia de ligação (BE) de um núcleo é a energia necessária para separá-lo em prótons e nêutrons individuais. Em termos de massas atômicas,\[BE = [(Zm(^1H) + Nm_n] - m(^AX)]c^2, \nonumber\] onde\(m(^1H)\) está a massa de um átomo de hidrogênio,\(m(^AX)\) é a massa atômica do nuclídeo e\(m_n\) é a massa de um nêutron. Padrões na energia de ligação por núcleo,\(BE/A\), revelam detalhes da força nuclear. Quanto maior o\(BE/A\), mais estável é o núcleo.

Glossário

energia vinculativa: a energia necessária para separar o núcleo em prótons e nêutrons individuais

energia de ligação por núcleo: a energia de ligação calculada por núcleo; revela os detalhes da força nuclear — quanto maior, mais estável é o núcleo\(BE/A\)