30.3: Teoria do Átomo de Hidrogênio de Bohr

Objetivos de

Ao final desta seção, você poderá:

• Descreva os mistérios dos espectros atômicos.
• Explique a teoria de Bohr sobre o átomo de hidrogênio.
• Explique o modelo planetário do átomo de Bohr.
• Ilustre o estado da energia usando o diagrama do nível de energia.
• Descreva os triunfos e os limites da teoria de Bohr.

O grande físico dinamarquês Niels Bohr (1885-1962) fez uso imediato do modelo planetário do átomo de Rutherford. (Figura\(\PageIndex{1}\)). Bohr se convenceu de sua validade e passou parte de 1912 no laboratório de Rutherford. Em 1913, depois de retornar a Copenhague, ele começou a publicar sua teoria do átomo mais simples, o hidrogênio, baseada no modelo planetário do átomo. Durante décadas, muitas perguntas foram feitas sobre as características atômicas. De seus tamanhos a seus espectros, muito se sabia sobre átomos, mas pouco havia sido explicado em termos das leis da física. A teoria de Bohr explicou o espectro atômico do hidrogênio e estabeleceu princípios novos e amplamente aplicáveis na mecânica quântica.

Figura\(\PageIndex{1}\). Niels Bohr, físico dinamarquês, usou o modelo planetário do átomo para explicar o espectro atômico e o tamanho do átomo de hidrogênio. Suas muitas contribuições para o desenvolvimento da física atômica e da mecânica quântica, sua influência pessoal em muitos estudantes e colegas e sua integridade pessoal, especialmente em face da opressão nazista, lhe renderam um lugar de destaque na história. (crédito: Autor desconhecido, via Wikimedia Commons)

Mistérios dos espectros atômicos

Conforme observado em “Quantização da Energia”, as energias de alguns sistemas pequenos são quantizadas. Sabe-se há mais de um século que os espectros de emissão e absorção atômica e molecular são discretos (ou quantizados) (Figura\(\PageIndex{2}\)). Maxwell e outros perceberam que deve haver uma conexão entre o espectro de um átomo e sua estrutura, algo como as frequências ressonantes dos instrumentos musicais. Mas, apesar dos anos de esforços de muitas grandes mentes, ninguém tinha uma teoria viável. (Era uma piada corrente que qualquer teoria dos espectros atômicos e moleculares poderia ser destruída jogando nela um livro de dados, tão complexos eram os espectros.) Seguindo a proposta de Einstein de fótons com energias quantizadas diretamente proporcionais aos seus comprimentos de onda, ficou ainda mais evidente que os elétrons nos átomos só podem existir em órbitas discretas.

Figura\(\PageIndex{2}\): A parte (a) mostra, da esquerda para a direita, um tubo de descarga, uma fenda e uma grade de difração produzindo um espectro de linha. A parte (b) mostra o espectro da linha de emissão de ferro. As linhas discretas implicam estados de energia quantizados para os átomos que as produzem. O espectro de linha para cada elemento é único, fornecendo uma ferramenta analítica poderosa e muito usada, e muitos espectros de linha foram bem conhecidos por muitos anos antes de poderem ser explicados com a física. (crédito para (b): Yttrium91, Wikimedia Commons)

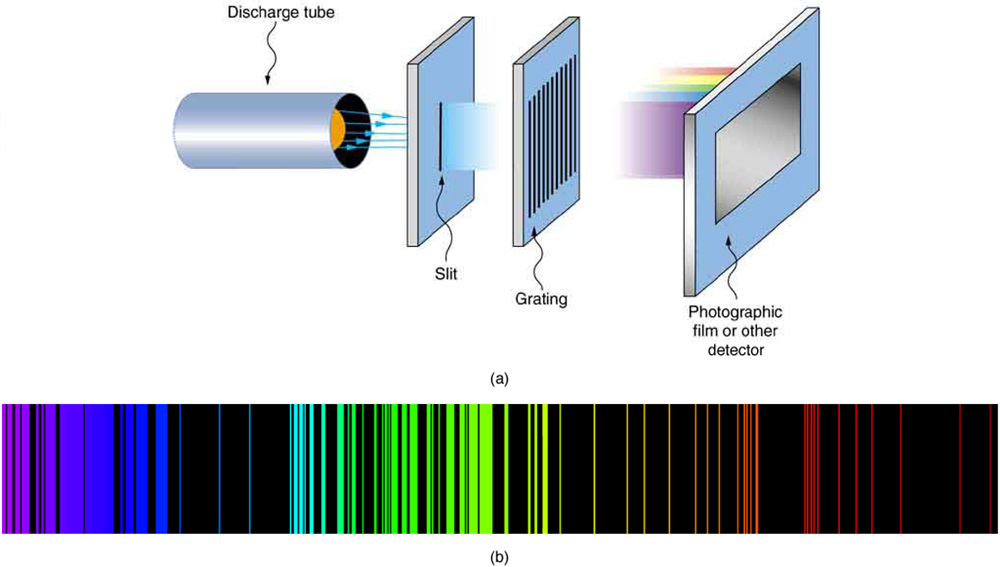
Em alguns casos, foi possível criar fórmulas que descrevessem os espectros de emissão. Como era de se esperar, o átomo mais simples — hidrogênio, com seu único elétron — tem um espectro relativamente simples. O espectro de hidrogênio foi observado no infravermelho (IR), visível e ultravioleta (UV), e várias séries de linhas espectrais foram observadas. (Veja a Figura\(\PageIndex{3}\).) Essas séries têm o nome de pesquisadores antigos que as estudaram em particular profundidade.

Os comprimentos de onda observados no espectro de hidrogênio podem ser calculados usando a seguinte fórmula:

\[\frac{1}{\lambda} = R \left( \frac{1}{n_{f}^{2}} - \frac{1}{n_{i}^{2}} \right), \label{30.4.1}\]

onde\(\lambda\) é o comprimento de onda da radiação EM emitida e\(R\) é a constante de Rydberg, determinada pelo experimento como sendo

\[R = 1.097 \times 10^{7}/m \left( or m^{-1} \right).\label{30.4.2}\]

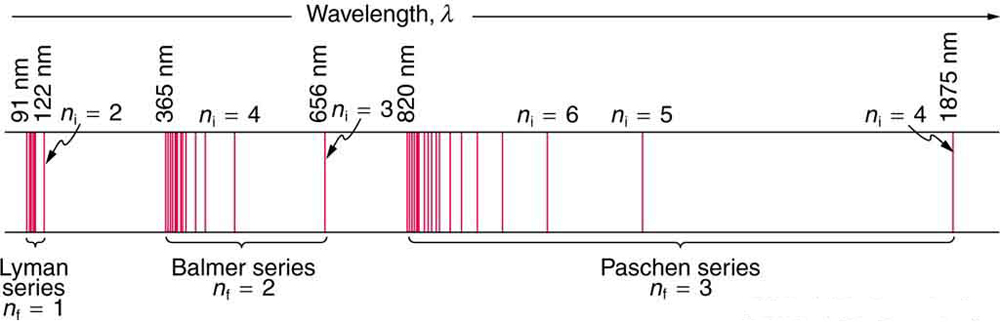
A constante\(n_{f}\) é um número inteiro positivo associado a uma série específica. Para a série Lyman,\(n_{f} = 1\); para a série Balmer,\(n_{f} = 2\); para a série Paschen,\(n_{f} = 3\); e assim por diante. A série Lyman é totalmente UV, enquanto parte da série Balmer é visível com o restante UV. A série Paschen e todo o resto são inteiramente infravermelhos. Aparentemente, há um número ilimitado de séries, embora elas se encontrem progressivamente mais longe no infravermelho e se tornem difíceis de observar à medida que\(n_{f}\) aumentam. A constante\(n_{i}\) é um número inteiro positivo, mas deve ser maior que\(n_{f}\). Assim, para a série Balmer,\( n_{f} = 2\)\(n_{i} = 3, 4, 5, 6, \cdot \cdot \cdot\) e. Observe que\(n_{i}\) pode se aproximar do infinito. Embora a fórmula na equação dos comprimentos de onda fosse apenas uma receita projetada para ajustar os dados e não fosse baseada em princípios físicos, ela implicava um significado mais profundo. Balmer primeiro desenvolveu a fórmula apenas para sua série, e mais tarde descobriu-se que ela descrevia todas as outras séries usando valores diferentes de\(n_{f}\). Bohr foi o primeiro a compreender o significado mais profundo. Novamente, vemos a interação entre experimento e teoria em física. Experimentalmente, os espectros estavam bem estabelecidos, descobriu-se que uma equação se encaixava nos dados experimentais, mas faltava a base teórica.

Figura\(\PageIndex{3}\): Um esquema do espectro de hidrogênio mostra várias séries nomeadas em homenagem àquelas que mais contribuíram para sua determinação. Parte da série Balmer está no espectro visível, enquanto a série Lyman está inteiramente em UV, e a série Paschen e outras estão no IR. Os valores de\(n_{f}\) e\(n_{i}\) são mostrados para algumas das linhas.

Exemplo\(\PageIndex{1}\): Calculating Wave Interference of a Hydrogen Line

Qual é a distância entre as fendas de uma grade que produz um máximo de primeira ordem para a segunda linha Balmer em um ângulo de\(15^{\circ}\)?

Estratégia e conceito:

Para um problema de conceito integrado, devemos primeiro identificar os princípios físicos envolvidos. Neste exemplo, precisamos saber (a) o comprimento de onda da luz, bem como (b) as condições para um máximo de interferência para o padrão a partir de uma fenda dupla. A parte (a) trata de um tópico do presente capítulo, enquanto a parte (b) considera o material de interferência de ondas de “Wave Optics”.

Solução para (a):

Comprimento de onda do espectro de hidrogênio. A série Balmer exige isso\(n_{f} = 2\). A primeira linha da série é considerada para\(n_{i} = 3\), e então a segunda teria\(n_{i} = 4\).

O cálculo é uma aplicação direta da equação do comprimento de onda. Inserindo os valores determinados\(n_{f}\) e os\(n_{i}\) rendimentos

\[ \begin{align*} \frac{1}{\lambda} = R \left( \frac{1}{n_{f}^{2}} - \frac{1}{n_{i}^{2}} \right) \label{30.4.3} \\[5pt] &= \left(1.097 \times 10^{7} m^{-1}\right) \left( \frac{1}{2^{2}} - \frac{1}{4^{2}} \right) \\[5pt] &= 2.057 \times 10^{6} m^{-1}. \end{align*}\]

Discussão para (a):

Esse é, de fato, o comprimento de onda observado experimentalmente, correspondente à segunda linha (azul-verde) da série Balmer. Mais impressionante é o fato de que a mesma receita simples prevê todas as linhas do espectro de hidrogênio, incluindo as novas observadas em experimentos subsequentes. O que a natureza está nos dizendo?

Solução para (b):

Interferência de fenda dupla (“Wave Optics”). Para obter interferência construtiva para uma fenda dupla, a diferença do comprimento do caminho de duas fendas deve ser um múltiplo integral do comprimento de onda. Essa condição foi expressa pela equação

\[d \sin{\theta} = m \lambda, \nonumber \]

onde\(d\) está a distância entre as fendas e\(\theta\) é o ângulo da direção original do feixe. O número\(m\) é a ordem da interferência;\(m=1\) neste exemplo. Resolver\(d\) e inserir valores conhecidos gera

\[d = \frac{\left(1\right) \left(486 nm\right)}{\sin{15^{\circ}}} = 1.88 \times 10^{-6} m. \nonumber\]

Discussão para (b):

Esse número é semelhante aos usados nos exemplos de interferência de “Introdução à Física Quântica” (e está próximo ao espaçamento entre fendas em óculos de difração comumente usados).

Solução de Bohr para hidrogênio

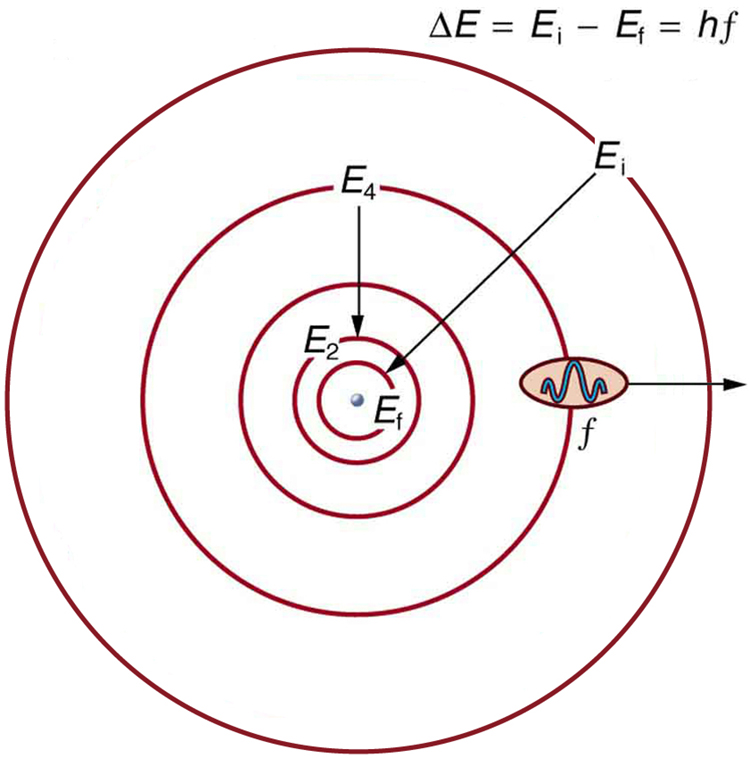
Bohr conseguiu derivar a fórmula do espectro de hidrogênio usando física básica, o modelo planetário do átomo e algumas novas propostas muito importantes. Sua primeira proposta é que apenas certas órbitas sejam permitidas: dizemos que as órbitas dos elétrons nos átomos são quantizadas. Cada órbita tem uma energia diferente, e os elétrons podem se mover para uma órbita mais alta absorvendo energia e cair para uma órbita inferior emitindo energia. Se as órbitas forem quantizadas, a quantidade de energia absorvida ou emitida também será quantizada, produzindo espectros discretos. A absorção e emissão de fótons estão entre os principais métodos de transferência de energia para dentro e para fora dos átomos. As energias dos fótons são quantizadas e sua energia é explicada como sendo igual à mudança na energia do elétron quando ele se move de uma órbita para outra. Em forma de equação, isso é

\[\Delta E = hf = E_{i} - E_{f}. \label{30.4.5}\]

Aqui,\(\Delta E\) está a mudança de energia entre as órbitas inicial e final, e\(hf\) é a energia do fóton absorvido ou emitido. É bastante lógico (ou seja, esperado de nossa experiência cotidiana) que a energia esteja envolvida na mudança de órbitas. Uma explosão de energia é necessária para que o ônibus espacial, por exemplo, suba para uma órbita mais alta. O que não se espera é que as órbitas atômicas sejam quantizadas. Isso não é observado em satélites ou planetas, que podem ter qualquer órbita com a energia adequada. (Veja a Figura\(\PageIndex{4}\).)

Figura\(\PageIndex{4}\): O modelo planetário do átomo, modificado por Bohr, tem as órbitas dos elétrons quantizadas. Somente certas órbitas são permitidas, explicando por que os espectros atômicos são discretos (quantizados). A energia transportada de um átomo por um fóton vem do elétron que cai de uma órbita permitida para outra e, portanto, é quantizada. Isso também vale para a absorção atômica de fótons.

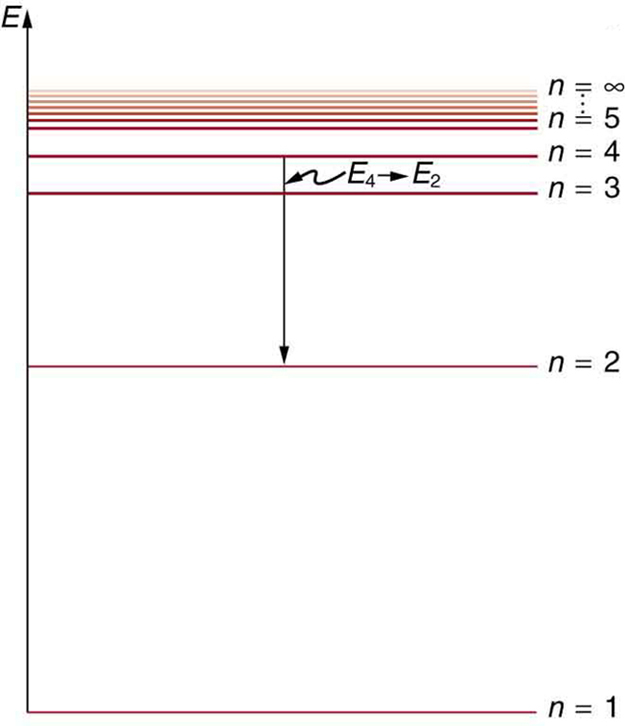
A Figura\(\PageIndex{5}\). mostra um diagrama do nível de energia, uma maneira conveniente de exibir os estados de energia. Na presente discussão, consideramos que esses são os níveis de energia permitidos do elétron. A energia é plotada verticalmente com o estado mais baixo ou fundamental na parte inferior e com os estados excitados acima. Dadas as energias das linhas em um espectro atômico, é possível (embora às vezes muito difícil) determinar os níveis de energia de um átomo. Diagramas de nível de energia são usados para muitos sistemas, incluindo moléculas e núcleos. Uma teoria do átomo ou qualquer outro sistema deve prever suas energias com base na física do sistema.

Figura\(\PageIndex{5}\). Um diagrama de nível de energia traça a energia verticalmente e é útil para visualizar os estados de energia de um sistema e as transições entre eles. Este diagrama é para os elétrons do átomo de hidrogênio, mostrando uma transição entre duas órbitas com energias\(E_{4}\)\(E_{2}\) e.

Bohr foi inteligente o suficiente para encontrar uma maneira de calcular as energias orbitais de elétrons no hidrogênio. Esse foi um primeiro passo importante que foi aprimorado, mas vale a pena repeti-lo aqui, porque ele descreve corretamente muitas características do hidrogênio. Assumindo órbitas circulares, Bohr propôs que o momento angular\(L\) de um elétron em sua órbita seja quantizado, ou seja, ele tem apenas valores específicos e discretos. O valor para\(L\) é dado pela fórmula\[L = m_{e}vr_{n} = n\frac{h}{2\pi} \left(n = 1,2,3, \cdot \cdot \cdot \right), \label{30.4.6}\] onde\(L\) é o momento angular,\(m_{e}\) é a massa do elétron,\(r_{n}\) é o raio da órbita e\(h\) é\(n\) a constante de Planck. Observe que o momento angular é\[L = I \omega. \label{30.4.7}\] Para um objeto pequeno em um raio\(r\),\[I = mr^{2}\label{30.4.8}\] e\[\omega = \frac{v}{r}\label{30.4.9}\], de modo que a\[L = \left(mr^{2}\right)\left(\frac{v}{r}\right) = mvr. \label{30.4.10}\] quantização diz que esse valor de só\(mvr\) pode ser igual a\(h/2, 2h/2, 3h/2\), etc. Na época, o próprio Bohr não sabia por que o momento angular deveria ser quantizado, mas usando essa suposição, ele foi capaz de calcular as energias no espectro de hidrogênio, algo que ninguém mais havia feito na época.

A partir das suposições de Bohr, agora derivaremos uma série de propriedades importantes do átomo de hidrogênio da física clássica que abordamos no texto. Começamos observando que a força centrípeta que faz com que o elétron siga um caminho circular é fornecida pela força de Coulomb. Para ser mais geral, notamos que essa análise é válida para qualquer átomo de elétron único. Então, se um núcleo tem\(Z\) prótons (\(Z = 1\)para hidrogênio, 2 para hélio, etc.) e apenas um elétron, esse átomo é chamado de átomo semelhante ao hidrogênio. Os espectros de íons semelhantes ao hidrogênio são semelhantes ao hidrogênio, mas deslocados para maior energia pela maior força de atração entre o elétron e o núcleo. A magnitude da força centrípeta é\(m_e v^2/r_n\), enquanto a força de Coulomb é\(k(Zq_e)(q_e)/r_n^2\). A suposição tácita aqui é que o núcleo é mais massivo que o elétron estacionário e o elétron orbita em torno dele. Isso é consistente com o modelo planetário do átomo. Igualando esses,

\[k\dfrac{Zq_e^2}{r_n^2} = \dfrac{m_e v^2}{r_n} (Coulomb = centripetal).\]

A quantização do momento angular é declarada em uma equação anterior. Resolvemos essa equação\(v\), a substituímos pela anterior e reorganizamos a expressão para obter o raio da órbita. Isso produz:\[r_n = \dfrac{n^2}{Z} a_B, \, for \, allowed \, orbits \, (n = 1, \, 2, \, 3, . . . ),\]

onde\(a_B\) é definido como sendo o raio de Bohr, já que para a órbita mais baixa (\( n = 1 \)) e para hidrogênio\((Z = 1)\),\(r_1 = a_B\). Resta aos Problemas e Exercícios deste capítulo mostrar que o raio de Bohr é

\[a_B = \dfrac{h^2}{4 \pi^2 m_e kq_e^2} = 0.529 \times 10^{-10} \, m.\]

Essas duas últimas equações podem ser usadas para calcular os raios das órbitas eletrônicas permitidas (quantizadas) em qualquer átomo semelhante ao hidrogênio. É impressionante que a fórmula forneça o tamanho correto do hidrogênio, que é medido experimentalmente para estar muito próximo ao raio de Bohr. A equação anterior também nos diz que o raio orbital é proporcional a\(n^2\), conforme ilustrado na Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): As órbitas eletrônicas permitidas no hidrogênio têm os raios mostrados. Esses raios foram calculados pela primeira vez por Bohr e são dados pela equação\(r_n = \frac{n^2}{Z}a_B\). A órbita mais baixa tem o diâmetro verificado experimentalmente de um átomo de hidrogênio.

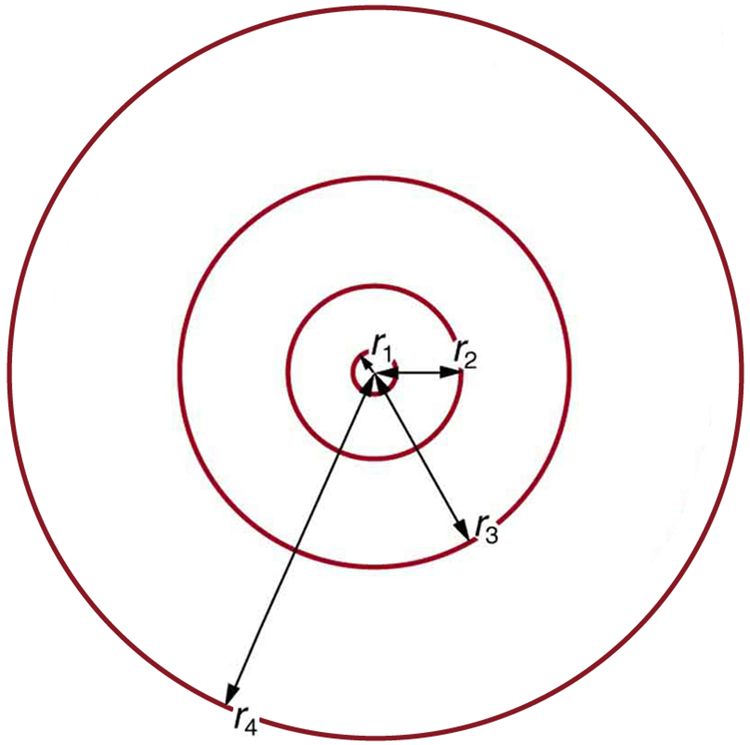
Para obter as energias orbitais dos elétrons, começamos observando que a energia do elétron é a soma de sua energia cinética e potencial: a energia\[ E_n = KE + PE.\] cinética é familiar\(KE = (1/2)m_e v^2\), supondo que o elétron não esteja se movendo em velocidades relativísticas. A energia potencial para o elétron é elétrica\(PE = q_e V\), ou, onde\(V\) está o potencial devido ao núcleo, que parece uma carga pontual. O núcleo tem uma carga positiva\(Zq_e\); portanto\(V = kZq_e/r_n\), relembrando uma equação anterior para o potencial devido a uma carga pontual. Como a carga do elétron é negativa, vemos isso\(PE = -kZq_e/r_n\). Inserindo as expressões para\(KE\) e\(PE\), encontramos\[E_n = \dfrac{1}{2} m_ev^2 - k\dfrac{Zq_e^2}{r_n}.\]

Agora substituímos\(r_n\) e\(v\) de equações anteriores na expressão acima por energia. Rendimentos da manipulação algébrica\[E_n = \dfrac{Z^2}{n^2} E_0(n = 1, \, 2, \, 3, ...)\]

para as energias orbitais de átomos semelhantes a hidrogênio. Aqui,\(E_0\) está a energia do estado fundamental (\(n = 1)\)para hidrogênio)\((Z = 1)\) e é dada por

\[E_0 = \dfrac{2 \pi^2 Q_e^4 m_e k^2}{h^2} = 13.6 \, eV.\]

Assim, para o hidrogênio,

\[E_n = - \dfrac{13.6 \, eV}{n^2} (n = 1, \, 2, \, 3, ...).\]

\(\PageIndex{7}\)A figura mostra um diagrama de nível de energia para hidrogênio que também ilustra como as várias séries espectrais de hidrogênio estão relacionadas às transições entre os níveis de energia.

Figura\(\PageIndex{7}\): Diagrama do nível de energia para hidrogênio mostrando as séries de transições Lyman, Balmer e Paschen. As energias orbitais são calculadas usando a equação acima, derivada primeiramente por Bohr.

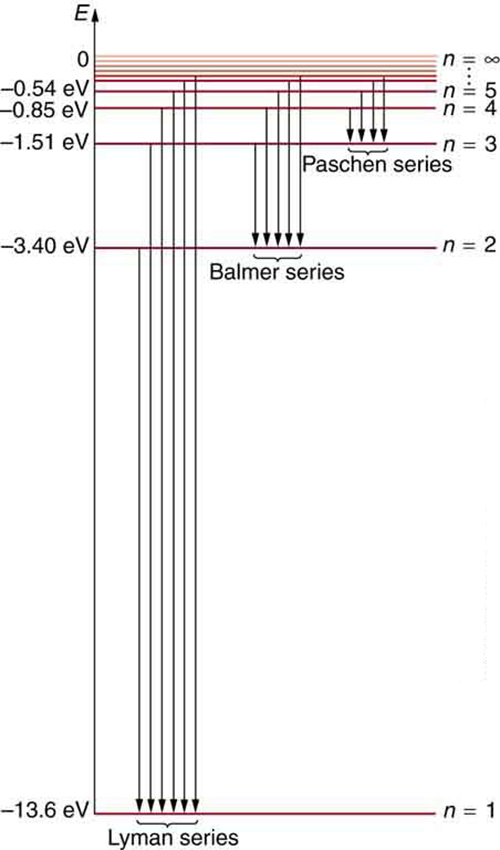
As energias totais dos elétrons são negativas, pois o elétron está ligado ao núcleo, análogo a estar em um buraco sem energia cinética suficiente para escapar. À medida que\(n\) se aproxima do infinito, a energia total se torna zero. Isso corresponde a um elétron livre sem energia cinética, pois\(r_N\) fica muito grande para grande\(n\), e a energia potencial elétrica, portanto, se torna zero. Assim, 13,6 eV são necessários para ionizar o hidrogênio (passar de —13,6 eV para 0, ou não ligado), um número verificado experimentalmente. Com mais energia, o elétron se desliga com alguma energia cinética. Por exemplo, dar 15,0 eV a um elétron no estado fundamental do hidrogênio o retira do átomo e o deixa com 1,4 eV de energia cinética.

Finalmente, vamos considerar a energia de um fóton emitida em uma transição descendente, dada pela equação como\[\Delta E = hf = E_i - E_f.\] Substituindo\(E_n = (-13.6 \, eV/n^2)\), vemos que\[hf = (13.6 \, eV)\left(\dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right).\]

Dividindo os dois lados dessa equação por\(hc\) dá uma expressão para\(1/\lambda\):

\[\dfrac{hf}{hc} = \dfrac{f}{c} = \dfrac{1}{\lambda} = \dfrac{(13.6 \, eV)}{hc} \left(\dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right).\]Pode-se mostrar que\[\left(\dfrac{13.6 \, eV}{hc} \right) = \dfrac{(13.6 \, eV)(1.602 \times 10^{-19} \, J/eV)}{(6.626 \, 10^{-34} \, J \cdot s)(2.998 \times 10^8 \, m/s)} = 1.097 \times 10^7 \, m^{-1} = R\] é a constante de Rydberg. Assim, usamos as suposições de Bohr para derivar a fórmula proposta pela primeira vez por Balmer anos antes como uma receita para ajustar os dados experimentais. \[\dfrac{1}{\lambda} = R \left(\dfrac{1}{n_f^2} - \dfrac{1}{n_i^2} \right)\]

Vemos que a teoria do átomo de hidrogênio de Bohr responde à pergunta sobre por que essa fórmula anteriormente conhecida descreve o espectro de hidrogênio. É porque os níveis de energia são proporcionais a\(1/n^2\), onde\(n\) está um número inteiro não negativo. Uma transição descendente libera energia e, portanto,\(n_i\) deve ser maior do que\(n_f\). As várias séries são aquelas em que as transições terminam em um determinado nível. Para a série Lyman,\(n_f = 1\) ou seja, todas as transições terminam no estado fundamental (veja também a Figura). Para a série Balmer,\(n_f = 2\), ou todas as transições terminam no primeiro estado de excitação; e assim por diante. O que antes era uma receita agora é baseado na física, e algo novo está surgindo: o momento angular é quantizado.

Triunfos e limites da teoria de Bohr

Bohr fez o que ninguém tinha sido capaz de fazer antes. Ele não apenas explicou o espectro do hidrogênio, ele calculou corretamente o tamanho do átomo a partir da física básica. Algumas de suas ideias são amplamente aplicáveis. As energias orbitais dos elétrons são quantizadas em todos os átomos e moléculas. O momento angular é quantizado. Os elétrons não entram em espiral no núcleo, como esperado classicamente (cargas aceleradas irradiam, de modo que as órbitas dos elétrons decairiam classicamente rapidamente e os elétrons ficariam no núcleo - a matéria entraria em colapso). Esses são grandes triunfos.

Mas há limites para a teoria de Bohr. Não pode ser aplicado a átomos de vários elétrons, mesmo um tão simples quanto um átomo de hélio de dois elétrons. O modelo de Bohr é o que chamamos de semiclássico. As órbitas são quantizadas (não clássicas), mas são consideradas caminhos circulares simples (clássicos). À medida que a mecânica quântica foi desenvolvida, ficou claro que não existem órbitas bem definidas; em vez disso, existem nuvens de probabilidade. A teoria de Bohr também não explicou que algumas linhas espectrais são duplas (divididas em duas) quando examinadas de perto. Examinaremos muitos desses aspectos da mecânica quântica com mais detalhes, mas deve-se ter em mente que Bohr não falhou. Em vez disso, ele deu passos muito importantes no caminho para um maior conhecimento e lançou as bases para toda a física atômica que evoluiu desde então.

EXPLORAÇÕES DE PHET: MODELOS DO ÁTOMO DE HIDROGÊNIO

Como os cientistas descobriram a estrutura dos átomos sem olhar para eles? Experimente diferentes modelos fotografando luz no átomo. Verifique como a previsão do modelo corresponde aos resultados experimentais.

Figura\(\PageIndex{8}\): Modelos do átomo de hidrogênio

Resumo

• O modelo planetário do átomo mostra elétrons orbitando o núcleo da mesma forma que os planetas orbitam o sol. Bohr usou o modelo planetário para desenvolver a primeira teoria razoável do hidrogênio, o átomo mais simples. Os espectros atômicos e moleculares são quantizados, com comprimentos de onda do espectro de hidrogênio dados pela fórmula\[\dfrac{1}{\lambda} = R\left(\dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right), \nonumber\] onde\(\lambda\) é o comprimento de onda da radiação EM emitida e\(R\) é a constante de Rydberg, que tem o valor\[R = 1.097 \times 10^7 \, m^{-1}. \nonumber\]
• As constantes\(n_i\) e\(n_f\) são números inteiros positivos e\(n_i\) devem ser maiores que\(n_f\).
• Bohr propôs corretamente que a energia e os raios das órbitas dos elétrons nos átomos sejam quantizados, com energia para transições entre órbitas dada por\[\Delta E = hf = E_i - E_f,\] onde\(\Delta E\) está a mudança de energia entre as órbitas inicial e final e\(hf\) é a energia de um fóton absorvido ou emitido. É útil traçar as energias orbitais em um gráfico vertical chamado diagrama de nível de energia.
• Bohr propôs que as órbitas permitidas são circulares e devem ter quantizado o momento angular orbital dado por\[L = m_evr_n = n\dfrac{h}{2\pi} (n = 1, \, 2, \, 3, . . .), \nonumber\] onde\(L\) está o momento angular,\(r_n\) é o raio da órbita\(n\) enésima e\(h\) é a constante de Planck. Para todos os átomos de um elétron (semelhantes a hidrogênio), o raio de uma órbita\[r_n = \dfrac{n^2}{Z}a_B(allowed \, orbits \, n = 1, \, 2, \, 3, ...), \nonumber\]\(Z\) é dado por é o número atômico de um elemento (o número de elétrons tem quando neutro) e\(a_B\) é definido como o raio de Bohr, que é\[a_B = \dfrac{h^2}{4 \pi^2m_ekq_e^2} = 0.529 \times 10^{-10} \, m. \nonumber\]
• Além disso, as energias dos átomos semelhantes ao hidrogênio são dadas por\[E_n = - \dfrac{Z^2}{n^2}E_0 (n = 1, \, 2, \, 3 ... ), \nonumber\] onde\(E_0\) está a energia do estado fundamental e são dadas por\[E_0 = \dfrac{2 \pi^2 q_e^4m_ek^2}{h^2} = 13.6 \, eV. \nonumber\] Assim, para o hidrogênio,\[E_n = - \dfrac{13.6 \, eV}{n^2} (n = 1, \, 2, \, 3, . . .). \nonumber\]
• A Teoria de Bohr fornece valores precisos para os níveis de energia em átomos semelhantes a hidrogênio, mas foi aprimorada em vários aspectos.

Glossário

comprimentos de onda do espectro de hidrogênio

os comprimentos de onda da luz visível do hidrogênio; pode ser calculado por\(\frac{1}{\lambda} = R \left(\frac{1}{n_f^2} - \frac{1}{n_i^2} \right)\)

Constante de Rydberg

uma constante física relacionada aos espectros atômicos com um valor estabelecido de\(1.097 \times 10^7 \, m^{-1}\)

interferência de dupla fenda

um experimento no qual ondas ou partículas de uma única fonte colidem com duas fendas para que o padrão de interferência resultante possa ser observado

diagrama do nível de energia

um diagrama usado para analisar o nível de energia dos elétrons nas órbitas de um átomo

Raio de Bohr

o raio médio da órbita de um elétron ao redor do núcleo de um átomo de hidrogênio em seu estado fundamental

átomo semelhante a hidrogênio

qualquer átomo com apenas um único elétron

energias de átomos semelhantes a hidrogênio

Fórmula de Bohr para energias de estados de elétrons em átomos semelhantes a hidrogênio:\(E_n = - \frac{Z^2}{n^2} E_0 (n = 1, \, 2, \, 3, . . . )\)