28.6: Energia relativista

Objetivos de

Ao final desta seção, você poderá:

• Calcule a energia total de um objeto relativista.
• Calcule a energia cinética de um objeto relativista.
• Descreva a energia de repouso e explique como ela pode ser convertida em outras formas.
• Explique por que partículas massivas não podem atingir C.

Um tokamak é uma forma de reator de fusão experimental, que pode transformar massa em energia. Conseguir isso requer uma compreensão da energia relativista. Os reatores nucleares são a prova da conservação da energia relativista.

Figura$\PageIndex{1}$: O National Spherical Torus Experiment (NSTX) tem um reator de fusão no qual isótopos de hidrogênio passam por fusão para produzir hélio. Nesse processo, uma massa relativamente pequena de combustível é convertida em uma grande quantidade de energia. (crédito: Princeton Plasma Physics Laboratory)

A conservação da energia é uma das leis mais importantes da física. Não só a energia tem muitas formas importantes, mas cada forma pode ser convertida em qualquer outra. Sabemos que, classicamente, a quantidade total de energia em um sistema permanece constante. Relativisticamente, a energia ainda é conservada, desde que sua definição seja alterada para incluir a possibilidade de mudança de massa para energia, como nas reações que ocorrem dentro de um reator nuclear. A energia relativista é definida intencionalmente para que seja conservada em todos os quadros inerciais, assim como é o caso do momento relativístico. Como consequência, aprendemos que várias quantidades fundamentais estão relacionadas de maneiras não conhecidas na física clássica. Todas essas relações são verificadas por experimentos e têm consequências fundamentais. A definição alterada de energia contém alguns dos novos insights mais fundamentais e espetaculares da natureza encontrados na história recente.

Energia total e energia de descanso

O primeiro postulado da relatividade afirma que as leis da física são as mesmas em todos os quadros inerciais. Einstein mostrou que a lei de conservação de energia é válida relativisticamente, se definirmos energia para incluir um fator relativista.

Definição: Energia total

A energia total$E$ é definida como

$$E = \gamma mc^2,$$

onde$m$ é massa,$c$ é a velocidade da luz e$v$ é a velocidade da massa em relação a um observador.$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$

Há muitos aspectos da energia total$E$ que discutiremos — entre eles estão como as energias cinéticas e potenciais são incluídas$E$ e como$E$ estão relacionadas ao momento relativístico. Mas primeiro, observe que, em repouso, a energia total não é zero. Em vez disso$v = 0$, quando temos$\gamma = 1$ e um objeto tem energia de repouso.

Definição: Energia de descanso

A energia de descanso é

$$E_0 = mc^2.$$

Essa é a forma correta da equação mais famosa de Einstein, que pela primeira vez mostrou que a energia está relacionada à massa de um objeto em repouso. Por exemplo, se a energia for armazenada no objeto, sua massa restante aumenta. Isso também implica que a massa pode ser destruída para liberar energia. As implicações dessas duas primeiras equações em relação à energia relativista são tão amplas que não foram completamente reconhecidas por alguns anos depois que Einstein as publicou em 1907, nem a prova experimental de que elas estão corretas foi amplamente reconhecida inicialmente. Einstein, deve-se notar, compreendeu e descreveu os significados e implicações de sua teoria.

Exemplo$\PageIndex{1}$: Calculating Rest Energy: Rest Energy is Very Large

Calcule a energia restante de uma massa de 1,00 g.

Estratégia

Um grama é uma massa pequena — menos da metade da massa de um centavo. Podemos multiplicar essa massa, em unidades SI, pela velocidade da luz ao quadrado para encontrar a energia de repouso equivalente.

Solução

1. Identifique os conhecidos:$m = 1.00 \times 10^{-3} \, kg$;$c = 3.00 \times 10^8 \, m/s$
2. Identifique o desconhecido:$E_0$
3. Escolha a equação apropriada:$E_0 = mc^2$
4. Insira os conhecidos na equação: $$\begin{align*} E_0 &= mc^2 \\[4pt] &= (1.00 \times 10^{-3} \, kg)(3.00 \times 10^8 \, m/s)^2 \\[4pt] &= 9.00 \times 10^{13} \, kg \cdot m^2/s^2 \end{align*}$$
5. Converta unidades.

Observando que\(1 \, kg \cdot m^2/s^2 = 1 \, J\), we see the rest mass energy is $$E_0 = 9.00 \times 19^{13} \, J.$$

Discussão

É uma quantidade enorme de energia para uma massa de 1,00 g. Não percebemos essa energia, porque geralmente ela não está disponível. A energia de repouso é grande porque a velocidade da luz$c^2$ é um número muito grande, então isso$mc^2$ é enorme para qualquer massa macroscópica. A energia de massa$9.00 \times 10^{13} \, J$ restante para 1,00 g é cerca de duas vezes a energia liberada pela bomba atômica de Hiroshima e cerca de 10.000 vezes a energia cinética de um grande porta-aviões. Se for possível encontrar uma maneira de converter a energia da massa restante em alguma outra forma (e todas as formas de energia podem ser convertidas umas nas outras), então grandes quantidades de energia podem ser obtidas com a destruição da massa.

Hoje, as aplicações práticas da conversão de massa em outra forma de energia, como em armas nucleares e usinas nucleares, são bem conhecidas. Mas também existiam exemplos quando Einstein propôs pela primeira vez a forma correta da energia relativista e descreveu alguns deles. A radiação nuclear havia sido descoberta na década anterior e era um mistério sobre a origem de sua energia. A explicação foi que, em certos processos nucleares, uma pequena quantidade de massa é destruída e a energia é liberada e transportada pela radiação nuclear. Mas a quantidade de massa destruída é tão pequena que é difícil detectar a falta de alguma. Embora Einstein tenha proposto isso como a fonte de energia nos sais radioativos que estavam sendo estudados, muitos anos se passaram até que houvesse um amplo reconhecimento de que a massa poderia ser e, de fato, comumente é convertida em energia (Figura$\PageIndex{1}$).

Figura$\PageIndex{2}$: O Sol (a) e a Estação Elétrica a Vapor Susquehanna (b) convertem massa em energia - o Sol via fusão nuclear, a estação elétrica via fissão nuclear. (créditos: (a) NASA/Goddard Space Flight Center, Estúdio de Visualização Científica; (b) governo dos EUA)

Por causa da relação da energia de repouso com a massa, agora consideramos a massa como uma forma de energia em vez de algo separado. Não havia sequer um indício disso antes do trabalho de Einstein. Essa conversão agora é conhecida por ser a fonte da energia do Sol, a energia da decomposição nuclear e até mesmo a fonte de energia que mantém o interior da Terra quente.

Energia armazenada e energia potencial

O que acontece com a energia armazenada em um objeto em repouso, como a energia colocada em uma bateria ao carregá-la ou a energia armazenada na mola comprimida de uma arma de brinquedo? A entrada de energia se torna parte da energia total do objeto e, assim, aumenta sua massa restante. Toda energia armazenada e potencial se torna massa em um sistema. Por que normalmente não notamos isso? De fato, a conservação da massa (significando que a massa total é constante) foi uma das grandes leis verificadas pela ciência do século XIX. Por que não foi percebido como incorreto? O exemplo a seguir ajuda a responder a essas perguntas.

Exemplo$\PageIndex{2}$: Calculating Rest Mass: A Small Mass Increase due to Energy Input

A bateria de um carro é classificada para ser capaz de mover 600 amperes-hora$( \cdot h)$ de carga a 12,0 V.

1. Calcule o aumento na massa restante dessa bateria quando ela é levada de totalmente esgotada para totalmente carregada.
2. Que aumento percentual é esse, considerando que a massa da bateria é de 20,0 kg?

Estratégia

Na parte (a), primeiro devemos encontrar a energia armazenada na bateria, que é igual à que a bateria pode fornecer na forma de energia potencial elétrica. Desde então$PE_{elec} = qV$, temos que calcular a carga$q$ em$600 \, A \cdot h$, que é o produto da corrente$I$ e da hora$t$. Em seguida, multiplicamos o resultado por 12,0 V. Podemos então calcular o aumento de massa da bateria usando$\Delta E = PE_{elec} = (\Delta m)c^2$.

A parte (b) é uma proporção simples convertida em porcentagem.

Solução para (a)

1. Identifique os conhecidos:$I \cdot t = 600 \, A \cdot h$;$V = 12.0 \, V$;$c = 3.00 \times 10^8 \, m/s$
2. Identifique o desconhecido:$\delta m$
3. Escolha a equação apropriada:$PE_{elec} = (\Delta m)c^2$
4. Reorganize a equação para resolver o desconhecido:$\Delta m = \frac{PE_{elec}}{c^2}$
5. Conecte os conhecidos na equação: $$\Delta m = \dfrac{PE_{elec}}{c^2} = \dfrac{qV}{c^2} = \dfrac{(It)V}{c^2} = \dfrac{(600 \, A \cdot h)(12.0 \, V)}{(3.00 \times 10^8)^2}.$$ escreva amperes A como coulombs por segundo (C/s) e converta horas em segundos. $$\Delta m = \dfrac{(600 \, C/s \cdot h(\frac{3600 \, s}{1 \, h})(12.0 \, J/C)}{3.00 \times 10^8 \, m/s)^2}$$ $$= \dfrac{(2.16 \times 10^6 \, C)(12.0 \, J/C)}{(3.00 \times 10^8 \, m/s)^2}$$ Usando a conversão$1 \, kg \cdot m^2/c^2 = 1 \, J$, podemos escrever a massa como$\delta m = 2.88 \times 10^{-10} \, kg$.

Solução para (b)

1. Identifique os conhecidos:$\Delta m = 2.88 \times 10^{-10} \, kg$;$m = 20.0 \, kg$
2. Identifique o desconhecido:% de variação
3. Escolha a equação apropriada:$\% \, increase = \frac{\Delta m}{m} \times 100\%$
4. Insira os conhecidos na equação: $$\% \, increase = \dfrac{\delta m}{m} \times 100\% = \dfrac{2.88 \times 10^{-10} \, kg}{20.0 \, kg} \times 100\% = 1.44 \times 10^{-9}\%$$

Discussão

Tanto o aumento real da massa quanto o aumento percentual são muito pequenos, já que a energia é dividida por$c^2$ um número muito grande. Teríamos que ser capazes de medir a massa da bateria com uma precisão de um bilionésimo de um por cento, ou 1 parte em$10^{11}$, para perceber esse aumento. Não é de admirar que a variação de massa não seja facilmente observada. Na verdade, essa mudança de massa é tão pequena que podemos questionar como você pode verificar se ela é real. A resposta é encontrada em processos nucleares nos quais a porcentagem de massa destruída é grande o suficiente para ser medida. A massa do combustível de um reator nuclear, por exemplo, é mensuravelmente menor quando sua energia é usada. Nesse caso, a energia armazenada foi liberada (convertida principalmente em calor e eletricidade) e a massa restante diminuiu. Esse também é o caso quando você usa a energia armazenada em uma bateria, exceto que a energia armazenada é muito maior em processos nucleares, tornando a mudança na massa mensurável na prática e na teoria.

Energia cinética e o limite máximo de velocidade

A energia cinética é a energia do movimento. Classicamente, a energia cinética tem a expressão familiar$\frac{1}{2} mv^2$. A expressão relativista da energia cinética é obtida do teorema da energia do trabalho. Esse teorema afirma que a rede em um sistema entra em energia cinética. Se nosso sistema começa do repouso, então o teorema trabalho-energia é

$$W_{net} = KE.$$

Relativisticamente, em repouso, temos energia de descanso$E_0 = mc^2$. O trabalho aumenta isso para a energia total$E = \gamma mc^2$. Assim,

$$W_{net} = E - E_0 = \gamma mc^2 - mc^2 = (\gamma - 1)mc^2.$$

Relativisticamente, temos$W_{net} = KE_{rel}.$

Definição: Energia cinética relativista

A energia cinética relativista é

$$KE_{rel} = (\gamma - 1)mc^2.$$

Quando imóveis, temos$v = 0$ e

$$\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}} = 1,$$

para que$KE_{rel} = 0$ em repouso, como esperado. Mas a expressão para energia cinética relativista (como energia total e energia de repouso) não se parece muito com a clássica.$\frac{1}{2}mv^2$ Para mostrar que a expressão clássica para energia cinética é obtida em baixas velocidades, notamos que a expansão binomial para$\gamma$ em baixas velocidades dá

$$\gamma = 1 + \dfrac{1}{2} \dfrac{v^2}{c^2}.$$

Inserir isso na expressão de energia cinética relativista dá

$$KE_{rel} = \left[\dfrac{1}{2} \dfrac{v^2}{c^2} \right] mc^2 = \dfrac{1}{2}mv^2 = KE_{class}.$$

Então, na verdade, a energia cinética relativista se torna a mesma que a energia cinética clássica quando$v < < c$.

É ainda mais interessante investigar o que acontece com a energia cinética quando a velocidade de um objeto se aproxima da velocidade da luz. Sabemos que isso$\gamma$ se torna infinito à medida que se$v$ aproxima$c$, então isso$KE_{rel}$ também se torna infinito à medida que a velocidade se aproxima da velocidade da luz (Figura$\PageIndex{1}$). Uma quantidade infinita de trabalho (e, portanto, uma quantidade infinita de entrada de energia) é necessária para acelerar uma massa até a velocidade da luz.

Definição: Velocidade da luz

Nenhum objeto com massa pode atingir a velocidade da luz.

Portanto, a velocidade da luz é o limite máximo de velocidade para qualquer partícula com massa. Tudo isso é consistente com o fato de que velocidades menores do que$c$ sempre se somam a menos de$c$. Tanto a forma relativista da energia cinética quanto o limite máximo de velocidade$c$ foram confirmados em detalhes em vários experimentos. Não importa quanta energia seja investida na aceleração de uma massa, sua velocidade só pode se aproximar — e não atingir — a velocidade da luz.

Figura$\PageIndex{3}$: Este gráfico de$KE_{rel}$ versus velocidade mostra como a energia cinética se aproxima do infinito à medida que a velocidade se aproxima da velocidade da luz. Portanto, não é possível que um objeto com massa alcance a velocidade da luz. Também é$KE_{class}$ mostrada a energia cinética clássica, que é semelhante à energia cinética relativista em baixas velocidades. Observe que é necessária muito mais energia para atingir altas velocidades do que o previsto classicamente.

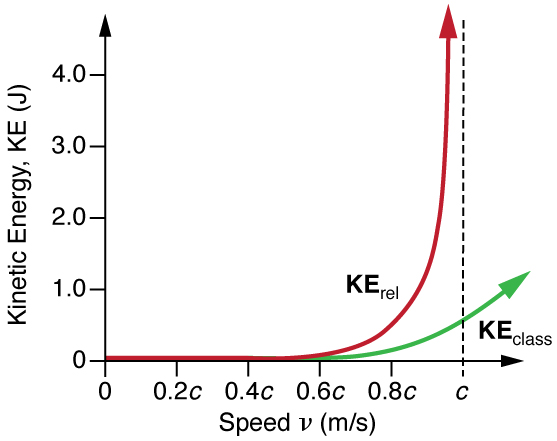
Exemplo$\PageIndex{3}$: Comparing Kinetic Energy: Relativistic Energy Versus Classical Kinetic Energy

Um elétron tem uma velocidade$v = 0.990 c$.

1. Calcule a energia cinética em MeV do elétron.
2. Compare isso com o valor clássico da energia cinética nessa velocidade. (A massa de um elétron é$9.11 \times 10^{-31} \, kg$.)

Estratégia

A expressão para energia cinética relativista está sempre correta, mas para (a) ela deve ser usada, pois a velocidade é altamente relativista (próxima de$c$). Primeiro, calcularemos o fator$\gamma$ relativístico e depois o usaremos para determinar a energia cinética relativista. Para (b), calcularemos a energia cinética clássica (que seria próxima do valor relativista se$v$ fosse menor que alguns por cento de$c$) e veremos que não é a mesma.

Solução para (a)

1. Identifique os conhecidos:$v = 0.990 c$;$m = 9.11 \times 10^{-31} \, kg$
2. Identifique o desconhecido:$KE_{rel}$
3. Escolha a equação apropriada$KE_{rel} = (\gamma - 1) mc^2$
4. Insira os conhecidos na equação:

Primeiro calcule$\gamma$. Carregaremos dígitos extras porque esse é um cálculo intermediário.

$$\gamma = \dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \frac{(0.990 c)^2}{c^2}}} = \dfrac{1}{\sqrt{1 - (0.990)^2}} = 7.0888$$

Em seguida, usamos esse valor para calcular a energia cinética.

$$KE_{rel} = (\gamma - 1)mc^2 = (7.0888 -1)(9.11 \times 10^{-31} \, kg)(3.00 \times 10^8 \, m/s)^2 = 4.99 \times 10^{-13} \, J$$

5. Unidades de conversão:

$$KE_{rel} = (4.99 \times 10^{-13} \, J)\left( \dfrac{1 \, MeV}{1.60 \times 10^{-13} \, J} \right) = 3.12 \, MeV$$

Solução para (b)

1. Liste os conhecidos:$v = 0.990 c$;$m = 9.11 \times 10^{-31} \, kg$
2. Liste o desconhecido:$KE_{class}$
3. Escolha a equação apropriada:$KE_{class} = \frac{1}{2} mv^2$
4. Insira os conhecidos na equação: $$KE_{class} = \dfrac{1}{2} mv^2$$ $$= \dfrac{1}{2}(9.11 \times 10^{-31} \, kg)(0.990)^2(3.00 \times 10^8 \, m/s)^2$$ $$= 4.02 \times 10^{-14} \, J$$
5. Unidades de conversão: $$KE_{class} = 4.02 \times 10^{-14} \, \left(\dfrac{1 \, MeV}{1.60 \times 10^{-13} \, J}\right) = 0.251 \, MeV$$

Discussão

Como era de se esperar, como a velocidade é de 99,0% da velocidade da luz, a energia cinética clássica está significativamente diferente do valor relativístico correto. Observe também que o valor clássico é muito menor do que o valor relativista. Na verdade,$KE_{rel}/KE_{class} = 12.4$ aqui. Isso é uma indicação de como é difícil fazer com que uma massa se mova perto da velocidade da luz. É necessária muito mais energia do que o previsto classicamente. Algumas pessoas interpretam essa energia extra como um aumento da massa do sistema, mas, conforme discutido em Relativistic Momentum, isso não pode ser verificado de forma inequívoca. O certo é que quantidades cada vez maiores de energia são necessárias para que a velocidade de uma massa fique um pouco mais próxima da da luz. Uma energia de 3 MeV é uma quantidade muito pequena para um elétron e pode ser alcançada com os aceleradores de partículas atuais. O SLAC, por exemplo, pode acelerar a superação dos elétrons$50 \times 10^9 \, eV = 50,000 MeV$.

Existe algum sentido em chegar$v$ um pouco mais perto de c do que 99,0% ou 99,9%? A resposta é sim. Aprendemos muito fazendo isso. A energia que entra em uma massa de alta velocidade pode ser convertida em qualquer outra forma, inclusive em massas inteiramente novas. (Veja a Figura.) Muito do que sabemos sobre a subestrutura da matéria e a coleção de partículas exóticas de vida curta na natureza foi aprendido dessa maneira. As partículas são aceleradas para energias extremamente relativistas e feitas para colidir com outras partículas, produzindo espécies totalmente novas de partículas. Os padrões nas características dessas partículas até então desconhecidas sugerem uma subestrutura básica para toda a matéria. Essas partículas e algumas de suas características serão abordadas em Física de Partículas.

Figura$\PageIndex{4}$: O Fermi National Accelerator Laboratory, perto de Batavia, Illinois, era um colisor de partículas subatômicas que acelerava prótons e antiprótons para atingir energias de até 1 Tev (um trilhão de elétronvolts). As lagoas circulares próximas aos anéis foram construídas para dissipar o calor residual. Esse acelerador foi desligado em setembro de 2011. (crédito: Fermilab, Reidar Hahn)

Energia e momento relativísticos

Sabemos classicamente que a energia cinética e o momento estão relacionados entre si, já que $$KE_{class} = \dfrac{p^2}{2m} = \dfrac{(mv)^2}{2m} = \dfrac{1}{2} mv^2.$$

Relativisticamente, podemos obter uma relação entre energia e momento manipulando algebricamente suas definições. Isso produz

$$E^2 = (pc)^2 + (mc^2)^2,$$

onde$E$ está a energia total relativista e$p$ é o momento relativístico. Essa relação entre energia relativista e momentum relativista é mais complicada do que a clássica, mas podemos obter algumas novas e interessantes percepções examinando-a. Primeiro, a energia total está relacionada ao momento e à massa de repouso. Em repouso, o momento é zero e a equação fornece a energia total como a energia restante$mc^2$ (portanto, essa equação é consistente com a discussão da energia de repouso acima). No entanto, à medida que a massa é acelerada, seu momentum$p$ aumenta, aumentando assim a energia total. Em velocidades suficientemente altas, o termo de energia restante$(mc^2)^2$ se torna insignificante em comparação com o termo de momento$(pc)^2$; portanto,$E = pc$ em velocidades extremamente relativistas.

Se considerarmos que$p$ o momento é distinto da massa, podemos determinar as implicações da equação$E^2 = (pc)^2 + (mc^2)^2$, para uma partícula que não tem massa. Se$m$ considerarmos zero nesta equação, então$E = pc$, ou$p = E/c$. Partículas sem massa têm esse impulso. Existem várias partículas sem massa encontradas na natureza, incluindo fótons (esses são quanta de radiação eletromagnética). Outra implicação é que uma partícula sem massa deve viajar em velocidade$c$ e somente em velocidade$c$. Embora esteja além do escopo deste texto examinar a relação na equação$E^2 = (pc)^2 + (mc^2)^2$, em detalhes, podemos ver que a relação tem implicações importantes na relatividade especial.

ESTRATÉGIAS DE RESOLUÇÃO DE PROBLEMAS PARA A RELATIVIDADE

1. Examine a situação para determinar se é necessário usar a relatividade. Os efeitos relativísticos estão relacionados ao$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$ fator relativista quantitativo. Se$\gamma$ for muito próximo de 1, então os efeitos relativísticos são pequenos e diferem muito pouco dos cálculos clássicos geralmente mais fáceis.
2. Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas).
3. Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos). Procure, em particular, informações sobre velocidade relativa$v$.
4. Certifique-se de entender os aspectos conceituais do problema antes de fazer qualquer cálculo. Decida, por exemplo, qual observador vê o tempo dilatado ou o comprimento contraído antes de inserir as equações. Se você pensou em quem vê o quê, quem está se movendo com o evento que está sendo observado, quem vê a hora certa e assim por diante, achará muito mais fácil determinar se seu cálculo é razoável.
5. Determine o principal tipo de cálculo a ser feito para encontrar as incógnitas identificadas acima. Você achará o resumo da seção útil para determinar se uma contração de comprimento, energia cinética relativista ou algum outro conceito está envolvido.
6. Não arredonde durante o cálculo. Conforme observado no texto, você geralmente deve realizar seus cálculos com vários dígitos para ver o efeito desejado. Você pode arredondar no final do problema, mas não use um número arredondado em um cálculo subsequente.
7. Verifique a resposta para ver se é razoável: Faz sentido? Isso pode ser mais difícil para a relatividade, já que não a encontramos diretamente. Mas você pode procurar velocidades maiores$c$ ou efeitos relativísticos que estão na direção errada (como uma contração temporal em que uma dilatação era esperada).

Exercício$\PageIndex{1}$

Um fóton decai em um par elétron-pósitron. Qual é a energia cinética do elétron se sua velocidade for$0.992 c$?

Resposta

$$\begin{align*} KE_{rel} &= (\gamma -1)mc^2 \\[5pt] &= \left(\dfrac{1}{\sqrt{1 - \frac{v^2}{c^2}}} - 1\right) mc^2 \\[5pt] &= \left( \dfrac{1}{\sqrt{1 - \frac{(0.992 c)^2}{c^2}}} - 1\right) (9.11 \times 10^{-31} \, kg)(3.00 \times 10^8 \, m/s)^2 \\[5pt] &= 5.67 \times 10^{-13} \, J \end{align*}$$

Resumo

• A energia relativista é conservada desde que a definamos para incluir a possibilidade de mudança de massa para energia.
• A energia total é definida como:$E = \gamma mc^2$, onde$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$
• A energia de repouso é$E_0 = mc^2$, o que significa que a massa é uma forma de energia. Se a energia for armazenada em um objeto, sua massa aumenta. A massa pode ser destruída para liberar energia.
• Normalmente, não notamos o aumento ou a diminuição da massa de um objeto porque a mudança na massa é muito pequena para um grande aumento na energia.
• O teorema relativístico da energia do trabalho é$W_{net} = E - E_0 = \gamma mc^2 = (\gamma - 1) mc^2$.
• Relativisticamente$W_{net} = KE_{rel}$,, onde$KE_{rel}$ está a energia cinética relativista.
• A energia cinética relativista é$KE_{rel} = (\gamma - 1) mc^2$, onde$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$. Em baixas velocidades, a energia cinética relativista é reduzida à energia cinética clássica.
• Nenhum objeto com massa pode atingir a velocidade da luz porque uma quantidade infinita de trabalho e uma quantidade infinita de entrada de energia são necessárias para acelerar uma massa até a velocidade da luz.
• A equação$E^2 = (pc)^2 + (mc^2)^2$ relaciona a energia total relativística$E$ e o momento relativístico$p$. Em velocidades extremamente altas, a energia restante$mc^2$ se torna insignificante,$E = pc$ e.

Glossário

energia total

definido como$E = \gamma mc^2$, onde$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$

energia de descanso

a energia armazenada em um objeto em repouso:$E_0 = mc^2$

energia cinética relativista

a energia cinética de um objeto se movendo em velocidades relativísticas:$KE_{rel} = (\gamma -1) mc^2$, onde$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$