28.4: Adição relativista de velocidades

Last updated
Save as PDF

Page ID: 194182

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Calcule a adição de velocidade relativista.
Explique quando a adição de velocidade relativística deve ser usada em vez da adição clássica de velocidades.
Calcule o deslocamento relativístico do Doppler.

Se você já viu um caiaque descendo um rio rápido, sabe que ficar no mesmo lugar seria difícil. A corrente do rio puxa o caiaque. Empurrar os remos contra a água pode fazer com que o caiaque avance na água, mas isso explica apenas parte da velocidade. O movimento do caiaque é um exemplo da adição clássica de velocidades. Na física clássica, as velocidades são adicionadas como vetores. A velocidade do caiaque é a soma vetorial de sua velocidade em relação à água e a velocidade da água em relação à margem do rio.

Um homem com um remo na mão está andando de caiaque rio abaixo em um rio raso e rápido. — Figura\(\PageIndex{1}\): A velocidade total de um caiaque, como este no rio Deerfield, em Massachusetts, é sua velocidade em relação à água, bem como a velocidade da água em relação à margem do rio. (crédito: abkfenris, Flickr)

Adição de velocidade clássica

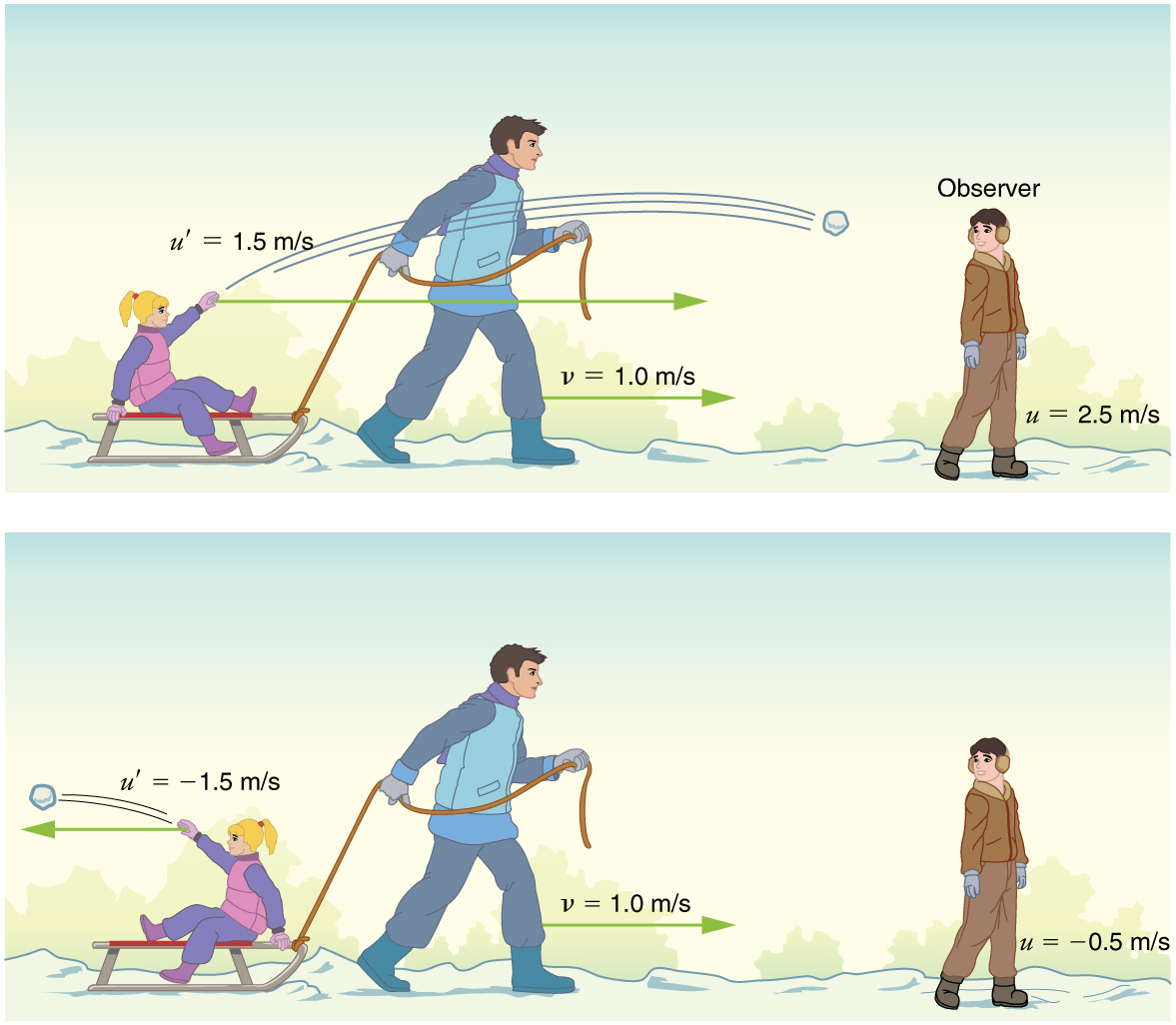
Para simplificar, restringimos nossa consideração da adição de velocidade ao movimento unidimensional. Classicamente, as velocidades se somam como números regulares em movimentos unidimensionais (Figura\(\PageIndex{1}\)). Suponha, por exemplo, que uma garota esteja andando em um trenó a uma velocidade de 1,0 m/s em relação a um observador. Ela lança uma bola de neve primeiro para frente e depois para trás a uma velocidade de 1,5 m/s em relação ao trenó. Denotamos direção com sinais de mais e menos em uma dimensão; neste exemplo, avançar é positivo. \(v\)Seja a velocidade do trenó em relação à Terra,\(u\) a velocidade da bola de neve em relação ao observador ligado à Terra e\(u'\) a velocidade da bola de neve em relação ao trenó.

Na parte a, um homem está puxando um trenó para a direita com uma velocidade v igual a um ponto zero metros por segundo. Uma garota sentada no trenó voltada para frente joga uma bola de neve em direção a um garoto na extremidade direita da foto. A bola de neve rotulada como u primed é igual a um ponto cinco metros por segundo na direção em que o trenó está sendo puxado. O menino é rotulado de dois pontos a cinco metros por segundo. Na figura b, uma figura semelhante é mostrada, mas a velocidade do homem é de um ponto zero metros por segundo, a garota está voltada para trás e joga a bola de neve atrás do trenó. A bola de neve é rotulada como u primed é igual a menos um ponto cinco metros por segundo, e o garoto é rotulado como u é igual a menos zero ponto cinco metros por segundo. — Figura\(\PageIndex{2}\): Classicamente, as velocidades somam como números comuns em movimentos unidimensionais. Aqui, a garota joga uma bola de neve para frente e depois para trás de um trenó. A velocidade do trenó em relação à Terra é\(v = 1.0 \, m/s\). A velocidade da bola de neve em relação ao caminhão é\(u'\), enquanto sua velocidade em relação à Terra é\(u\). Classicamente,\(u = v + u'\).

ADIÇÃO DE VELOCIDADE CLÁSSICA

\[u = v + u'\]

Assim, quando a garota joga a bola de neve para frente,\(U = 1.0 \, m/s + 1.5 \, m/s = 2.5 \, m/s\). Faz sentido intuitivo que a bola de neve vá em direção ao observador terrestre mais rapidamente, porque é lançada para frente a partir de um veículo em movimento. Quando a garota joga a bola de neve para trás,\(u = 1.0 \, m/s + (-1.5 \, m/s) = -0.5 \, m/s\). O sinal de menos significa que a bola de neve se afasta do observador que está na Terra.

Adição de velocidade relativista

O segundo postulado da relatividade (verificado por extensa observação experimental) diz que a adição clássica de velocidade não se aplica à luz. Imagine um carro viajando à noite por uma estrada reta, como na Figura\(\PageIndex{3}\). Se a adição clássica de velocidade fosse aplicada à luz, a luz dos faróis do carro se aproximaria do observador na calçada em alta velocidade\(u = v + c\). Mas sabemos que a luz se afastará do carro em alta velocidade em\(c\) relação ao motorista do carro, e a luz também se moverá em direção ao observador na calçada em alta velocidade\(c\).

Um carro está se movendo para a direita com velocidade v. Um menino parado na calçada observa o carro. A velocidade da luz u primed é mostrada como c conforme observada pela garota no carro e a velocidade da luz u também é c conforme observada pelo menino. — Figura: De\(\PageIndex{3}\) acordo com o experimento e o segundo postulado da relatividade, a luz dos faróis do carro se afasta do carro em alta velocidade e em\(c\) direção ao observador na calçada em alta velocidade.\(c\) A adição clássica de velocidade não é válida.

ADIÇÃO DE VELOCIDADE RELATIVISTA

Ou a luz é uma exceção, ou a fórmula clássica de adição de velocidade só funciona em baixas velocidades. O último é o caso. A fórmula correta para adição de velocidade relativista unidimensional é

\[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}},\]

onde\(v\) é a velocidade relativa entre dois observadores,\(u\) é a velocidade de um objeto em relação a um observador e\(u'\) é a velocidade relativa ao outro observador. (Para facilitar a visualização, geralmente optamos por medir\(u\) em nosso quadro de referência, enquanto alguém se move em\(v\) relação a nós mede\(u'\).) Observe que o termo\(\frac{vu'}{c^2}\) se torna muito pequeno em baixas velocidades e\(u = \frac{v + u}{1 + \frac{vu'}{v^2}}\) fornece um resultado muito próximo à adição de velocidade clássica. Como antes, vemos que a adição clássica de velocidade é uma excelente aproximação à fórmula relativista correta para velocidades pequenas. Não é de admirar que isso pareça correto em nossa experiência.

Exemplo\(\PageIndex{1}\): Showing that the Speed of Light towards an Observer is Constant (in a Vacuum): The Speed of Light is the Speed of Light

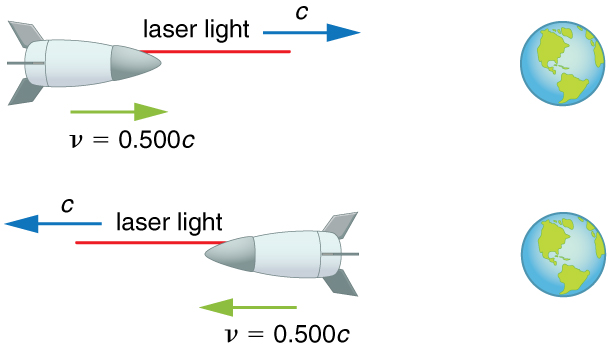
Suponha que uma nave espacial indo diretamente em direção à Terra na metade da velocidade da luz envie um sinal para nós em um feixe de luz produzido a laser. Dado que a luz sai da nave na velocidade observada a partir da nave, calcule a velocidade com que ela se aproxima da Terra.

Uma espaçonave está indo em direção à Terra v é igual a zero ponto cinco zero zero vezes c. Um feixe de laser da nave viaja em direção à Terra com a velocidade c, conforme mostrado por um vetor. Uma segunda nave espacial viajando para longe da Terra. A velocidade da segunda nave e do segundo laser é a mesma do primeiro, mas na direção oposta. — Figura\(\PageIndex{4}\)

Estratégia

Como a luz e a espaçonave estão se movendo em velocidades relativistas, não podemos usar a simples adição de velocidade. Em vez disso, podemos determinar a velocidade com que a luz se aproxima da Terra usando a adição de velocidade relativista.

Solução

Identifique os conhecidos:\(v = 0.500 c\);\(u' = c\)
Identifique o desconhecido:\(u\)
Escolha a equação apropriada:\(u = \frac{v + u'}{1 + \frac{vu'}{c^2}}\).
Insira os conhecidos na equação. \[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} = \dfrac{0.500 c + c}{1 + \frac{(0.500C)(c)}{c^2}} = \dfrac{(0.500 +1)c}{1 + \frac{0.500c^2}{c^2}} = \dfrac{1.500 c}{1 + 0.500} = \dfrac{1.500c}{1.500} + c\]

Discussão

A adição de velocidade relativista fornece o resultado correto. A luz sai do navio em alta velocidade

e se aproxima da Terra em alta velocidade\(c\). A velocidade da luz é independente do movimento relativo da fonte e do observador, esteja o observador na nave ou com destino à Terra.

As velocidades não podem ser maiores do que a velocidade da luz, desde que\(v\) seja menor\(c\) e\(u'\) não exceda\(c\). O exemplo a seguir ilustra que a adição de velocidade relativista não é tão simétrica quanto a adição de velocidade clássica.

Exemplo\(\PageIndex{2}\): Comparing the Speed of Light towards and away from an Observer: Relativistic Package Delivery

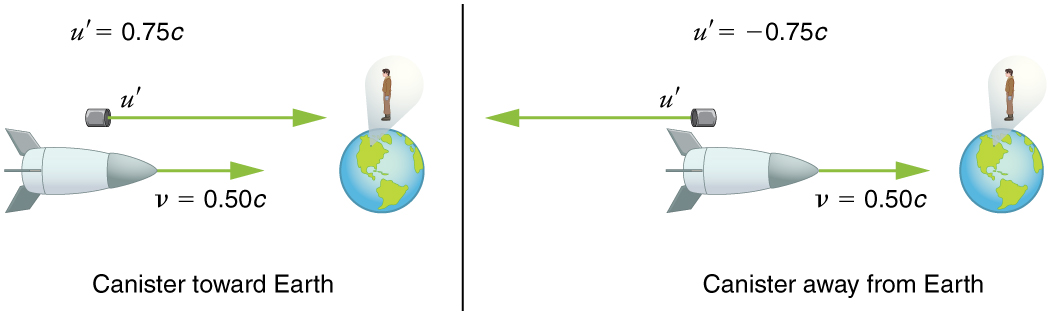
Suponha que a nave espacial no exemplo anterior esteja se aproximando da Terra na metade da velocidade da luz e atire em um recipiente a uma velocidade de\(0.750 c\).

A que velocidade um observador ligado à Terra verá o recipiente se ele for disparado diretamente em direção à Terra?
Se for disparado diretamente da Terra? (Figura\(\PageIndex{5}\)).

Na parte a, uma nave espacial está se movendo em direção à Terra da esquerda para a direita com uma velocidade v igual a zero ponto cinco zero vezes c. A espaçonave dispara um recipiente em direção à Terra com velocidade u prime igual a zero ponto sete cinco vezes c. Um homem fica parado na Terra observando. Na parte b, a espaçonave atira o recipiente para longe da Terra com a mesma velocidade. Em ambos os casos, a velocidade do navio é v igual a 0 ponto cinco zero vezes c para a esquerda. — Figura\(\PageIndex{5}\)

Estratégia

Como o recipiente e a nave espacial estão se movendo em velocidades relativísticas, devemos determinar a velocidade do recipiente por um observador ligado à Terra usando a adição de velocidade relativista em vez da simples adição de velocidade.

Solução para (a)

Identifique os conhecidos:\(v = 0.500 c\);\(u' = 0.750 c\)
Identifique o desconhecido:\(u\)
Escolha a equação apropriada:\(u = \frac{v + u'}{1 + \frac{vu'}{c^2}}\)
Insira os conhecidos na equação:\[ u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} = \dfrac{0.500 c + 0.750 c}{1 + \frac{(0.500 c)(0.750 c)}{c^2}} = \dfrac{1.250 c}{1 + 0.375)} = 0.909 c\]

Solução para (b)

Identifique os conhecidos:\(v = 0.500 c\);\(u' = -0.750 c\)
Identifique o desconhecido:\(u\)
Escolha a equação apropriada:\(u = \frac{v + u'}{1 + \frac{vu'}{c^2}}\)
Insira os conhecidos na equação:\[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} = \dfrac{0.500 c + (-0.750 c)}{1 + \frac{(0.500 C)(-0.750 c)}{c^2}} = \dfrac{-0.250 c}{1 - 0.375} = -0.400 c\]

Discussão

O sinal de menos indica a velocidade de distância da Terra (na direção oposta de\(v\)), o que significa que o recipiente está indo em direção à Terra em parte (a) e afastado em parte (b), conforme esperado. Mas as velocidades relativistas não são adicionadas de forma tão simples quanto fazem classicamente. Na parte (a), o recipiente se aproxima da Terra mais rápido, mas não com a simples soma de\(1.250 c\). A velocidade total é menor do que você obteria classicamente. E em parte (b), o recipiente se afasta da Terra a uma velocidade de\(-0.400c\), que é mais rápida do que\(-0.250 c\) você esperaria classicamente. As velocidades nem são simétricas. Em parte (a), o recipiente se move\(0.409 c\) mais rápido do que a nave em relação à Terra, enquanto em parte (b) ele se move\(0.900 c\) mais devagar que o navio.

Deslocamento Doppler

Embora a velocidade da luz não mude com a velocidade relativa, as frequências e os comprimentos de onda da luz mudam. Discutido pela primeira vez para ondas sonoras, um desvio de Doppler ocorre em qualquer onda quando há movimento relativo entre a fonte e o observador.

EFEITOS DOPPLER RELATIVÍSTICOS

O comprimento de onda observado da radiação eletromagnética é maior (chamado de desvio para o vermelho) do que o emitido pela fonte quando a fonte se afasta do observador e mais curto (chamado de desvio para o azul) quando a fonte se move em direção ao observador.

\[\lambda_{obs} = \lambda_s \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}}\]

Na equação de Doppler\(\lambda_{obs}\) está o comprimento de onda observado,\(\lambda_s\) o comprimento de onda da fonte e\(u\) a velocidade relativa da fonte para o observador. A velocidade\(u\) é positiva para o movimento afastado de um observador e negativa para o movimento em direção a um observador. Em termos de frequência da fonte e frequência observada, esta equação pode ser escrita.\[f_{obs} = f_s \sqrt{\dfrac{1 - \frac{u}{c}}{1 + \frac{u}{c}}}.\] Observe que os sinais — e + são diferentes dos da equação do comprimento de onda.

CONEXÃO DE CARREIRA: ASTRÔNOMO

Se você está interessado em uma carreira que exige um conhecimento da relatividade especial, provavelmente não há conexão melhor do que a astronomia. Os astrônomos devem levar em conta os efeitos relativísticos ao calcular distâncias, tempos e velocidades de buracos negros, galáxias, quasares e todos os outros objetos astronômicos. Para ter uma carreira em astronomia, você precisa de pelo menos um diploma de graduação em física ou astronomia, mas geralmente é necessário um mestrado ou doutorado. Você também precisa de uma boa formação em matemática de alto nível.

Exemplo\(\PageIndex{3}\): Calculating a Doppler Shift: Radio Waves from a Receding Galaxy

Suponha que uma galáxia esteja se afastando da Terra em alta velocidade\(0.825 c\). Ele emite ondas de rádio com um comprimento de onda de\(0.525 \, m\).

Que comprimento de onda detectaríamos na Terra?

Estratégia

Como a galáxia está se movendo a uma velocidade relativista, devemos determinar o desvio Doppler das ondas de rádio usando o deslocamento Doppler relativístico em vez do desvio Doppler clássico.

Solução

Identifique os conhecidos:\(u = 0.825 c\);\(\lambda_s = 0.525 \, m\)
Identifique o desconhecido:\(\lambda_{obs}\)
Escolha a equação apropriada:\(\lambda_{obs} = \lambda \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}}\)
Conecte os conhecidos na equação\[\lambda_{obs} = \lambda \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}} = (0.525 \, m)\sqrt{\dfrac{1 + \frac{0.825 c}{c}}{1 - \frac{0.825 c}{c}}} = 1.70 \, m.\]

Discussão

Como a galáxia está se afastando da Terra, esperamos que os comprimentos de onda da radiação que ela emite sejam desviados para o vermelho. O comprimento de onda que calculamos é de 1,70 m, que é desviado para o vermelho do comprimento de onda original de 0,525 m.

O desvio relativístico do Doppler é fácil de observar. Essa equação tem aplicações diárias que vão desde medições de velocidade de transporte por radar com desvio Doppler até monitoramento de tempestades por radar Doppler. Em observações astronômicas, o deslocamento relativístico do Doppler fornece informações de velocidade, como o movimento e a distância das estrelas.

Exercício\(\PageIndex{1}\)

Suponha que uma sonda espacial se afaste da Terra em alta velocidade\(0.350 c\). Ele envia uma mensagem de ondas de rádio de volta à Terra com uma frequência de 1,50 GHz. Com que frequência a mensagem é recebida na Terra?

Resposta: \[f_{obs} = f_c \sqrt{\dfrac{1 - \frac{u}{c}}{1 + \frac{u}{c}}} = (1.50 \, GHz) \sqrt{\dfrac{1 - \frac{0.350 c}{c}}{1 + \frac{0.350 c}{c}}} = 1.04 \, GHz \nonumber\]

Resumo

Com a adição clássica de velocidade, as velocidades somam como números regulares no movimento unidimensional:\(u = v + u'\), onde\(v\) é a velocidade entre dois observadores,\(u\) é a velocidade de um objeto em relação a um observador e\(u'\) é a velocidade relativa ao outro observador.
As velocidades não podem ser adicionadas para serem maiores do que a velocidade da luz. A adição de velocidade relativista descreve as velocidades de um objeto se movendo a uma velocidade relativista:\[u = \dfrac{v + u'}{1 + \frac{vu'}{c^2}} \nonumber\]
Um observador da radiação eletromagnética vê efeitos relativísticos do Doppler se a fonte da radiação estiver se movendo em relação ao observador. O comprimento de onda da radiação é maior (chamado de desvio para o vermelho) do que o emitido pela fonte quando a fonte se afasta do observador e menor (chamado de desvio para o azul) quando a fonte se move em direção ao observador. O comprimento de onda deslocado é descrito pela equação\[\lambda_{obs} = \lambda_s \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}} \nonumber\]\(\lambda_{obs}\) é o comprimento de onda observado,\(\lambda_s\) é o comprimento de onda da fonte e\(u\) é a velocidade relativa da fonte para o observador.

Glossário

adição de velocidade clássica: o método de adicionar velocidades quando\(v << c\), as velocidades somam como números regulares no movimento unidimensional:\(u = v + u'\), onde\(v\) é a velocidade entre dois observadores,\(u\) é a velocidade de um objeto em relação a um observador e\(u'\) é a velocidade relativa ao outro observador.

adição de velocidade relativista: o método de adicionar velocidades de um objeto movendo-se a uma velocidade relativística\(u \frac{v + u'}{1 + \frac{vu'}{c^2}}\), onde\(v\) é a velocidade relativa entre dois observadores,\(u\) é a velocidade de um objeto em relação a um observador e\(u'\) é a velocidade relativa ao outro observador

efeitos Doppler relativísticos: uma mudança no comprimento de onda da radiação que está se movendo em relação ao observador; o comprimento de onda da radiação é maior (chamado de desvio para o vermelho) do que o emitido pela fonte quando a fonte se afasta do observador e menor (chamado de desvio para o azul) quando a fonte se move em direção ao observador; o deslocado o comprimento de onda é descrito pela equação\[\lambda_{obs} = \lambda_s \sqrt{\dfrac{1 + \frac{u}{c}}{1 - \frac{u}{c}}}\] onde\(\lambda_{obs}\) é o comprimento de onda observado,\(\lambda_s\) é o comprimento de onda da fonte e\(u\) é a velocidade da fonte para o observador