23.E: Indução eletromagnética, circuitos de corrente alternada e tecnologias elétricas (exercício)
- Page ID
- 195043
Perguntas conceituais
23.1 Emf induzido e fluxo magnético
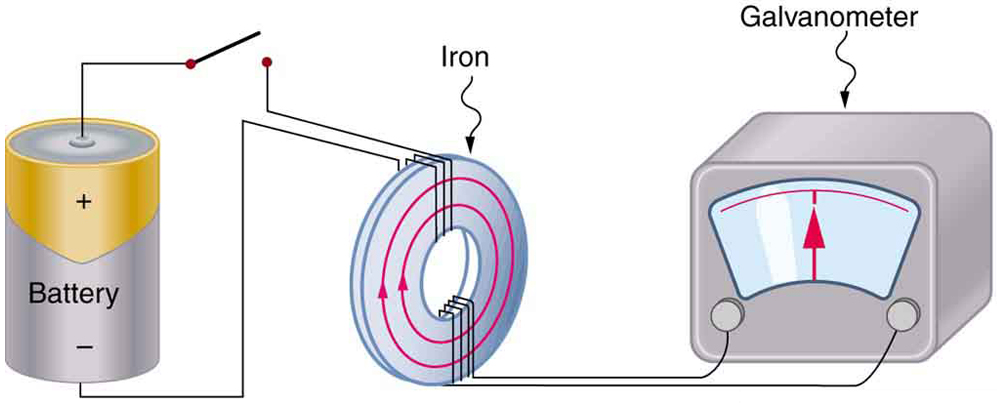
1. Como as bobinas de circuito múltiplo e o anel de ferro na versão do aparelho de Faraday mostrada na Figura aprimoram a observação da emf induzida?
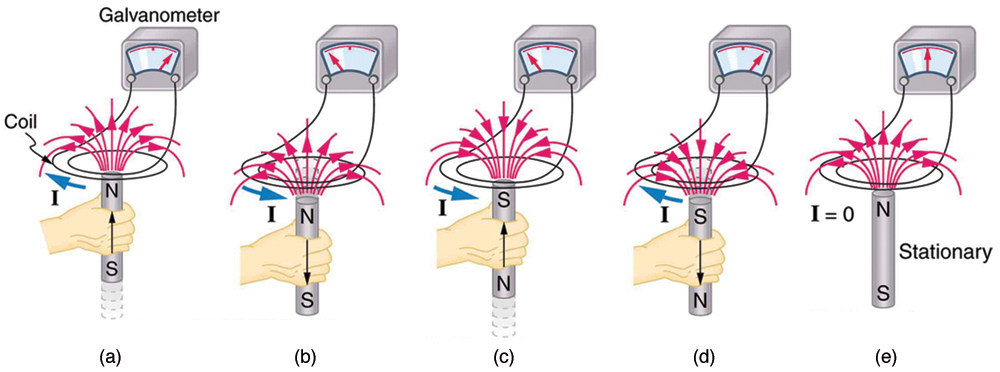
2. Quando um ímã é empurrado para dentro de uma bobina, como na Figura (a), qual é a direção da força exercida pela bobina no ímã? Desenhe um diagrama mostrando a direção da corrente induzida na bobina e o campo magnético que ela produz, para justificar sua resposta. Como a magnitude da força depende da resistência do galvanômetro?
3. Explique como o fluxo magnético pode ser zero quando o campo magnético não é zero.
4. Um emf é induzido na bobina da Figura quando ela é esticada? Em caso afirmativo, indique o porquê e dê a direção da corrente induzida.
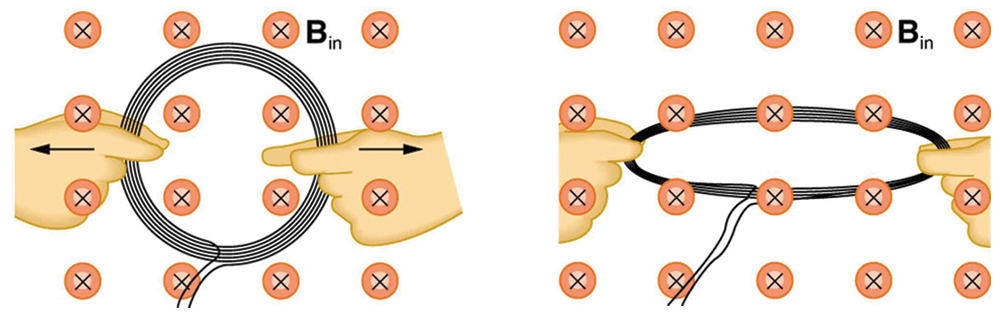
Uma bobina circular de fio é esticada em um campo magnético.
23.2 Lei da Indução de Faraday: Lei de Lenz
5. Uma pessoa que trabalha com ímãs grandes às vezes coloca a cabeça dentro de um campo forte. Ela relata sentir tontura ao virar a cabeça rapidamente. Como isso pode estar associado à indução?
6. Um acelerador de partículas envia partículas carregadas de alta velocidade por um tubo evacuado. Explique como uma bobina de fio enrolada no tubo pode detectar a passagem de partículas individuais. Esboce um gráfico da saída de tensão da bobina quando uma única partícula passa por ela.
23.3 Emf emocional
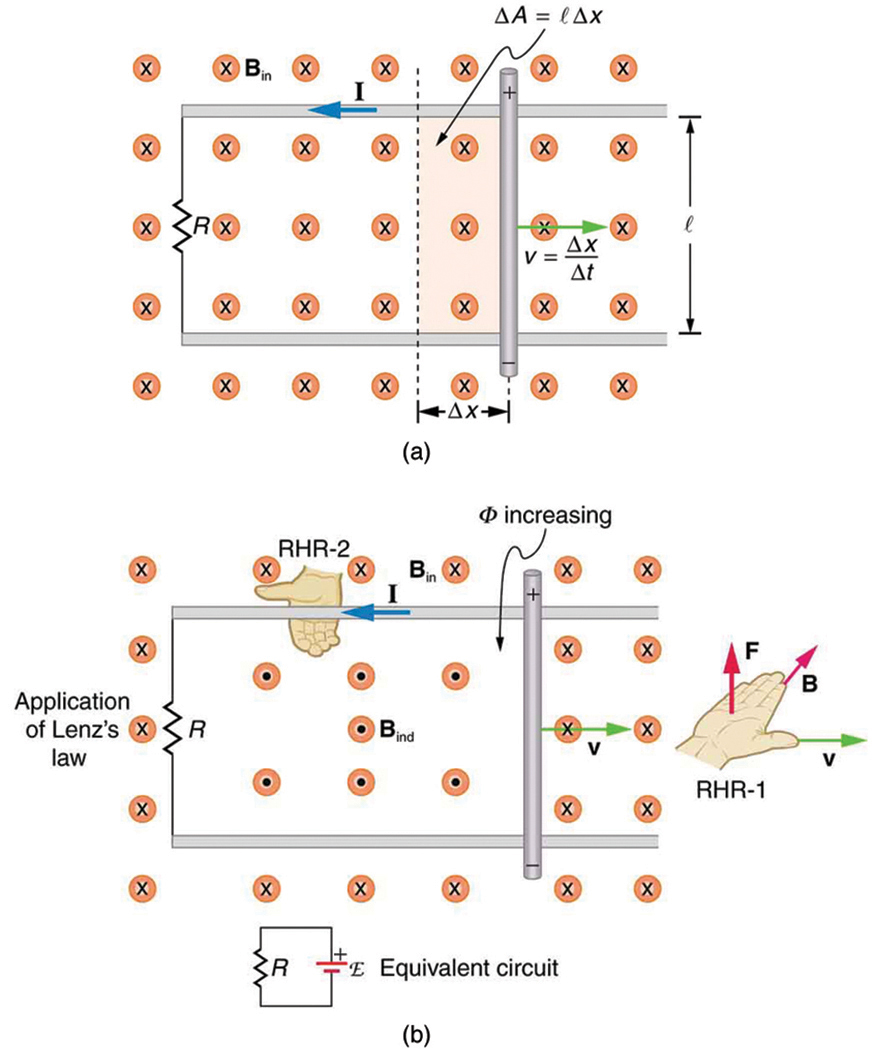
7. Por que parte do circuito deve estar se movendo em relação a outras partes, para ter emf mocional utilizável? Considere, por exemplo, que os trilhos na Figura são estacionários em relação ao campo magnético, enquanto a haste se move.
8. Um poderoso canhão de indução pode ser feito colocando um cilindro de metal dentro de uma bobina solenóide. O cilindro é expelido com força quando a corrente solenóide é ligada rapidamente. Use as leis de Faraday e Lenz para explicar como isso funciona. Por que o cilindro pode ficar vivo/quente quando o canhão é disparado?
9. Um fogão de indução aquece uma panela com uma bobina transportando uma corrente alternada localizada abaixo da panela (e sem uma superfície quente). A superfície do fogão pode ser um condutor? Por que uma bobina transportando corrente contínua não funciona?
10. Explique como você pode descongelar um cano de água congelada enrolando uma bobina carregando uma corrente alternada ao redor dele. Importa se o tubo é ou não um condutor? Explique.
23.4 Correntes parasitas e amortecimento magnético
11. Explique por que o amortecimento magnético pode não ser eficaz em um objeto feito de várias camadas condutoras finas separadas por isolamento.
12. Explique como a indução eletromagnética pode ser usada para detectar metais? Essa técnica é particularmente importante na detecção de minas terrestres enterradas para descarte, prospecção geofísica e em aeroportos.
23.5 Geradores elétricos
13. Usando o RHR-1, mostre que os emfs nas laterais do circuito do gerador na Figura estão no mesmo sentido e, portanto, adicione.
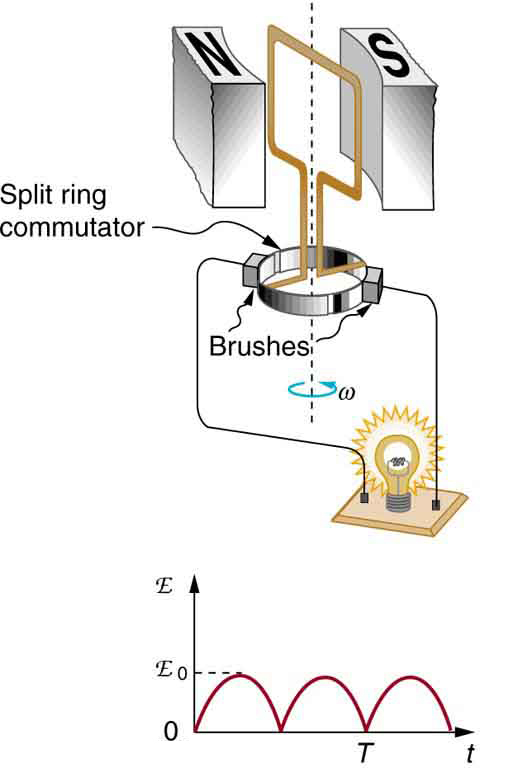
14. A fonte da produção de energia elétrica de um gerador é o trabalho realizado para girar suas bobinas. Como o trabalho necessário para girar o gerador está relacionado à lei de Lenz?
23.6 Emf preta
15. Suponha que você descubra que o acionamento por correia que conecta um motor potente a uma unidade de ar condicionado está quebrado e o motor está funcionando livremente. Você deve se preocupar com o fato de o motor estar consumindo uma grande quantidade de energia sem nenhum propósito útil? Explique por que ou por que não.
23.7 Transformadores
16. Explique o que causa vibrações físicas nos transformadores com o dobro da frequência da alimentação CA envolvida.
23.8 Segurança elétrica: sistemas e dispositivos
17. O isolamento de plástico em fios ativos/quentes evita riscos de choque, riscos térmicos ou ambos?
18. Por que disjuntores e fusíveis comuns são ineficazes na prevenção de choques?
19. Um GFI pode disparar apenas porque os fios ativos/quentes e neutros conectados a ele são significativamente diferentes em comprimento. Explique o porquê.
23.9 Indutância
20. Como você colocaria duas bobinas planas idênticas em contato para que elas tivessem a maior indutância mútua? O mínimo?
21. Como você moldaria um determinado comprimento de fio para obter a maior autoindutância? O mínimo?
22. Verifique, conforme concluído sem prova no Exemplo, que as unidades de\(\displaystyle T⋅m^2/A=Ω⋅s=H\).
23.11 Reatância, indutiva e capacitiva
23. A presbiacusia é uma perda auditiva decorrente da idade que afeta progressivamente as frequências mais altas. Um amplificador de aparelho auditivo foi projetado para amplificar todas as frequências igualmente. Para ajustar sua saída para presbiacusia, você colocaria um capacitor em série ou em paralelo com o alto-falante do aparelho auditivo? Explique.
24. Você usaria uma grande indutância ou uma grande capacitância em série com um sistema para filtrar baixas frequências, como o zumbido de 100 Hz em um sistema de som? Explique.
25. O ruído de alta frequência na alimentação AC pode danificar os computadores. A unidade de encaixe projetada para evitar esse dano usa uma grande indutância ou uma grande capacitância (em série com o computador) para filtrar essas altas frequências? Explique.
26. A indutância depende da corrente, da frequência ou de ambas? E quanto à reatância indutiva?
27. Explique por que o capacitor na Figura (a) atua como um filtro de baixa frequência entre os dois circuitos, enquanto o da Figura (b) atua como um filtro de alta frequência.
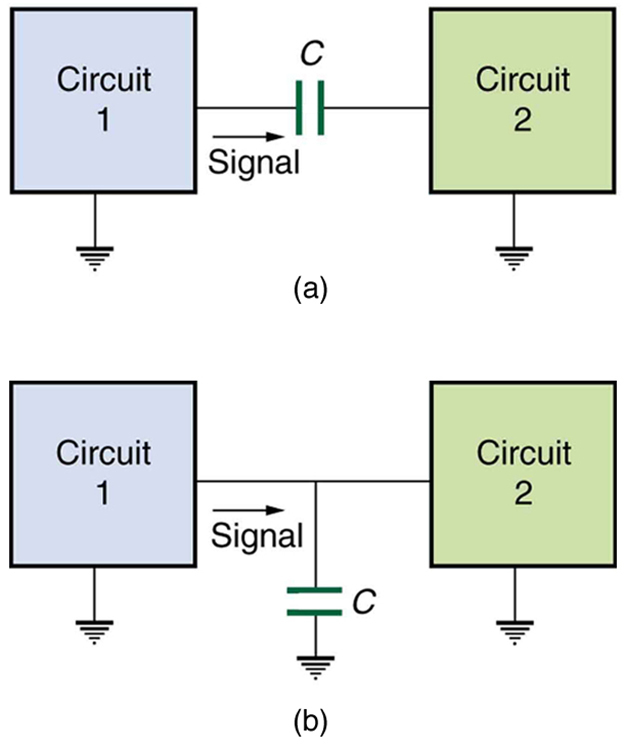
Capacitores e indutores. Capacitor com alta frequência e baixa frequência.
28. Se os capacitores na Figura forem substituídos por indutores, que atuam como um filtro de baixa frequência e quais como um filtro de alta frequência?
23.12 Circuitos AC da série RLC
29. A frequência de ressonância de um circuito CA depende do pico de tensão da fonte CA? Explique por que ou por que não.
30. Suponha que você tenha um motor com um fator de potência significativamente menor que 1. Explique por que seria melhor melhorar o fator de potência como um método para melhorar a saída do motor, em vez de aumentar a entrada de tensão.
Problemas e exercícios
23.1 Emf induzido e fluxo magnético
31. Qual é o valor do fluxo magnético na bobina 2 na Figura devido à bobina 1?
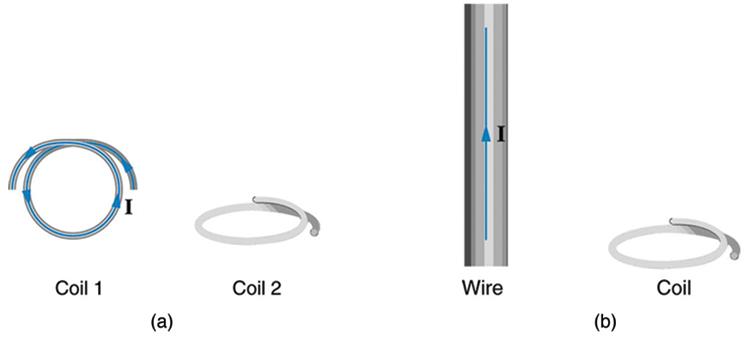
(a) Os planos das duas bobinas são perpendiculares. (b) O fio é perpendicular ao plano da bobina.
Solução
Zero
32. Qual é o valor do fluxo magnético através da bobina na Figura (b) devido ao fio?
23.2 Lei da Indução de Faraday: Lei de Lenz
33. Referindo-se à Figura (a), qual é a direção da corrente induzida na bobina 2:
(a) Se a corrente na bobina 1 aumentar?
(b) Se a corrente na bobina 1 diminuir?
(c) Se a corrente na bobina 1 for constante? Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para a Lei de Lenz.
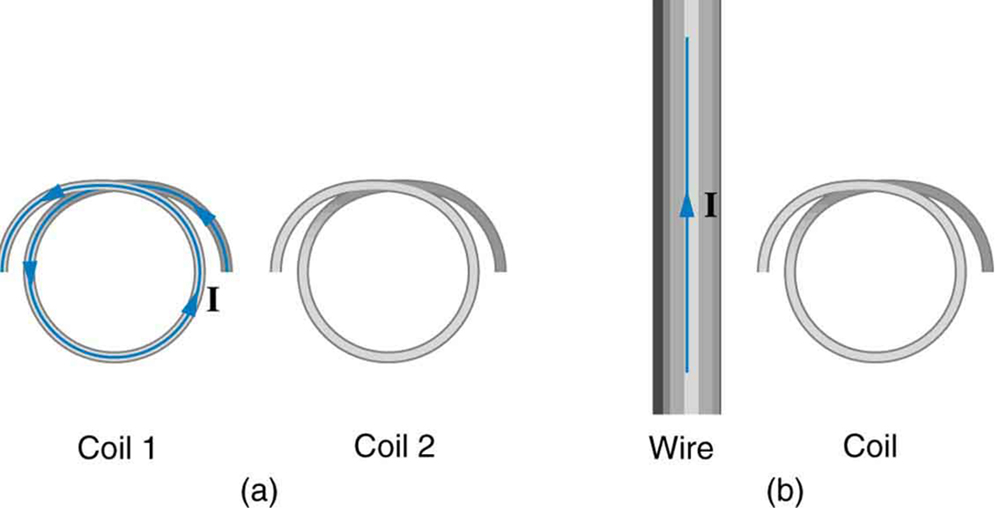
(a) As bobinas estão no mesmo plano. (b) O fio está no plano da bobina
Solução
(a) CCW
(b) CW
(c) Nenhuma corrente induzida
34. Referindo-se à Figura (b), qual é a direção da corrente induzida na bobina:
(a) Se a corrente no fio aumentar?
(b) Se a corrente no fio diminuir?
(c) Se a corrente no fio mudar repentinamente de direção? Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para a Lei de Lenz.
35. Referindo-se à Figura, quais são as direções das correntes nas bobinas 1, 2 e 3 (suponha que as bobinas estejam no plano do circuito):
(a) Quando o interruptor é fechado pela primeira vez?
(b) Quando o interruptor está fechado há muito tempo?
(c) Logo após a abertura do interruptor?
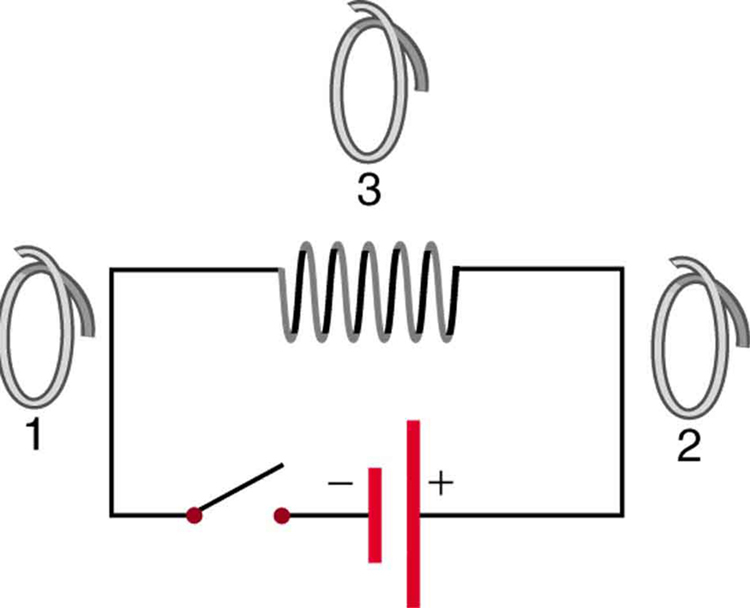
Solução
(a) 1 CCW, 2 CCW, 3 CW
(b) 1, 2 e 3 sem corrente induzida
(c) 1 CW, 2 CW, 3 CCW
36. Repita o problema anterior com a bateria invertida.
37. Verifique se as unidades de\(\displaystyle ΔΦ/Δt\) são volts. Ou seja, mostre isso\(\displaystyle 1T⋅m^2/s=1V\).
38. Suponha que uma bobina de 50 voltas esteja no plano da página em um campo magnético uniforme direcionado para a página. A bobina originalmente tem uma área de\(\displaystyle 0.250m^2\). Ele é esticado para não ter área em 0,100 s. Qual é a direção e a magnitude do emf induzido se o campo magnético uniforme tiver uma intensidade de 1,50 T?
39. (a) Um técnico de ressonância magnética move a mão de uma região de muito baixa intensidade de campo magnético para o campo de 2,00 T de um scanner de ressonância magnética com os dedos apontando na direção do campo. Encontre o emf médio induzido em sua aliança de casamento, dado que seu diâmetro é de 2,20 cm e assumindo que são necessários 0,250 s para movê-lo para o campo. (b) Discuta se essa corrente alteraria significativamente a temperatura do anel.
Solução
(a) 3,04 mV
(b) Como limite inferior no anel, estime R = 1,00 mΩ. O calor transferido será de 2,31 mJ. Isso não é uma quantidade significativa de calor.
40. Conceitos integrados
Referindo-se à situação do problema anterior:
(a) Qual corrente é induzida no anel se sua resistência for 0,0100\(\displaystyle Ω\)?
(b) Qual potência média é dissipada?
(c) Qual campo magnético é induzido no centro do anel? (d) Qual é a direção do campo magnético induzido em relação ao campo da ressonância magnética?
41. Um emf é induzido pela rotação de uma bobina de 1000 voltas e 20,0 cm de diâmetro no campo\(\displaystyle 5.00×10^{−5}T\) magnético da Terra. Qual emf médio é induzido, dado que o plano da bobina é originalmente perpendicular ao campo da Terra e é girado para ficar paralelo ao campo em 10,0 ms?
Solução
0,157 V
42. Uma bobina de 0,250 m de raio e 500 voltas é girada um quarto de uma revolução em 4,17 ms, originalmente tendo seu plano perpendicular a um campo magnético uniforme. (Isso é 60 rev/s.) Encontre a intensidade do campo magnético necessária para induzir uma emf média de 10.000 V.
43. Conceitos integrados
Aproximadamente como o emf induzido no circuito na Figura (b) depende da distância entre o centro do loop e o fio?
Solução
proporcional a\(\displaystyle \frac{1}{r}\)
44. Conceitos integrados
(a) Um raio produz um campo magnético que varia rapidamente. Se o parafuso atingir a terra verticalmente e agir como uma corrente em um fio longo e reto, ele induzirá uma tensão em um circuito alinhado como a da Figura (b). Qual voltagem é induzida em um circuito de 1,00 m de diâmetro 50,0 m a partir de um\(\displaystyle 2.00×10^6\) raio, se a corrente cair para zero\(\displaystyle 25.0 μs\)?
(b) Discuta as circunstâncias em que tal tensão produziria consequências perceptíveis.
23.3 Emf emocional
45. Use a lei de Faraday, a lei de Lenz e a RHR-1 para mostrar que a força magnética na corrente na haste móvel na Figura está na direção oposta à sua velocidade.

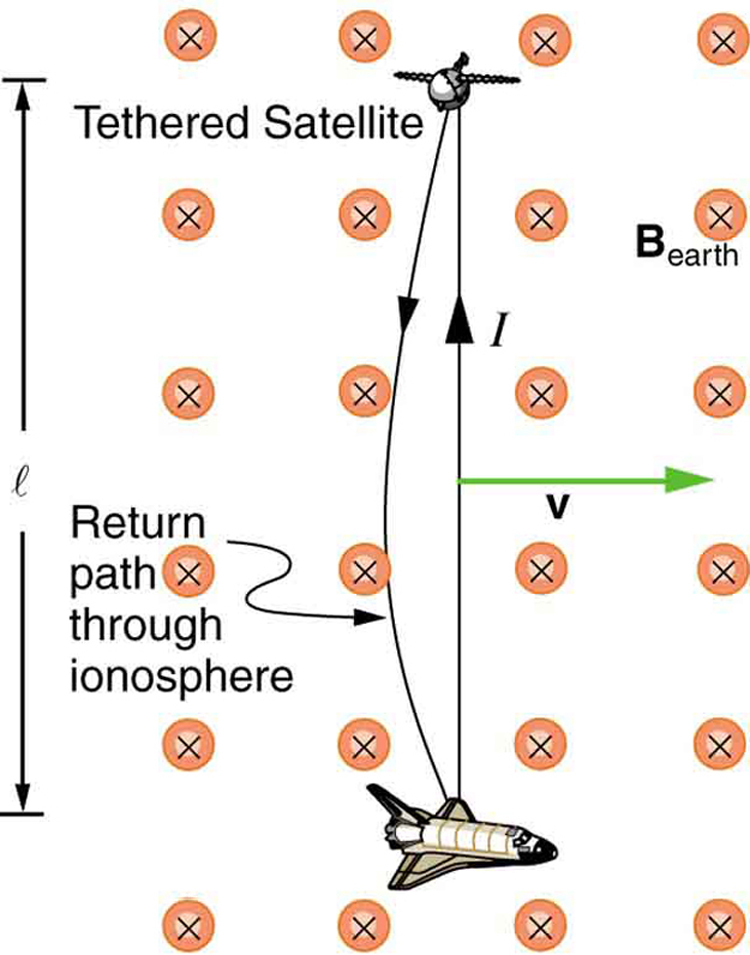
46. Se uma corrente fluir no Satellite Tether mostrado na Figura, use a lei de Faraday, a lei de Lenz e a RHR-1 para mostrar que há uma força magnética na corda na direção oposta à sua velocidade.
47. (a) Um avião a jato com uma envergadura de 75,0 m está voando a 280 m/s. Qual emf é induzido entre as pontas das asas se o componente vertical do campo da Terra for\(\displaystyle 3.00×10^{−5}T\)?
(b) É provável que um emf dessa magnitude tenha alguma consequência? Explique.
Solução
(a) 0,630 V
(b) Não, este é um emf muito pequeno.
48. (a) Uma chave de fenda não ferrosa está sendo usada em um campo magnético de 2,00 T. Qual emf máximo pode ser induzido ao longo de seu comprimento de 12,0 cm quando ele se move a 6,00 m/s?
(b) É provável que esse emf tenha alguma consequência ou mesmo seja notado?
49. Em que velocidade a haste deslizante na Figura deve se mover para produzir um emf de 1,00 V em um campo de 1,50 T, dado que o comprimento da haste é de 30,0 cm?

Solução
2,22 m/s
50. A haste de 12,0 cm de comprimento na Figura se move a 4,00 m/s. Qual é a intensidade do campo magnético se um emf de 95,0 V for induzido?
51. Prove que quando\(\displaystyle B, ℓ,\) e não\(\displaystyle v\) são mutuamente perpendiculares, emf mocional é dado por\(\displaystyle emf=Bℓvsinθ\). Se\(\displaystyle v\) for perpendicular a\(\displaystyle B\), então\(\displaystyle θ\) é o ângulo entre\(\displaystyle ℓ\)\(\displaystyle B\) e. Se\(\displaystyle ℓ\) for perpendicular a\(\displaystyle B\), então\(\displaystyle θ\) é o ângulo entre\(\displaystyle v\)\(\displaystyle B\) e.
52. No voo do ônibus espacial de agosto de 1992, apenas 250 m da corda condutora considerada em Example puderam ser soltos. Uma emf mocional de 40,0 V foi gerada no\(\displaystyle 5.00×10^{−5}T\) campo da Terra, enquanto se movia em\(\displaystyle 7.80×10^3m/s\). Qual era o ângulo entre a velocidade da nave auxiliar e o campo da Terra, supondo que o condutor fosse perpendicular ao campo?
53. Conceitos integrados
Derive uma expressão para a corrente em um sistema como o da Figura, sob as seguintes condições. A resistência entre os trilhos é\(\displaystyle R\) que os trilhos e a haste móvel são idênticos na seção transversal\(\displaystyle A\) e têm a mesma resistividade\(\displaystyle ρ\). A distância entre os trilhos é\(\displaystyle l\), e a haste se move a uma velocidade constante\(\displaystyle v\) perpendicular ao campo uniforme\(\displaystyle B\). No tempo zero, a haste móvel está próxima à resistência\(\displaystyle R\).
54. Conceitos integrados
O Satélite Tethered na Figura tem uma massa de 525 kg e está na extremidade de um cabo de 20,0 km de comprimento e 2,50 mm de diâmetro com a resistência à tração do aço.
(a) Quanto o cabo se estica se uma força de 100 N for exercida para puxar o satélite para dentro? (Suponha que o satélite e o ônibus espacial estejam na mesma altitude acima da Terra.)
(b) Qual é a constante de força efetiva do cabo?
(c) Quanta energia é armazenada nela quando esticada pela força de 100 N?
55. Conceitos integrados
O Satélite Tethered discutido neste módulo está produzindo 5,00 kV e uma corrente de fluxos de 10,0 A.
(a) Que força de arrasto magnético isso produz se o sistema estiver se movendo a 7,80 km/s?
(b) Quanta energia cinética é removida do sistema em 1,00 h, negligenciando qualquer mudança na altitude ou velocidade durante esse período?
(c) Qual é a mudança na velocidade se a massa do sistema for 100.000 kg?
(d) Discuta as consequências de longo prazo (digamos, uma missão de uma semana) na órbita do ônibus espacial, observando o efeito de uma diminuição na velocidade e avaliando a magnitude do efeito.
Solução
(a) 10,0 N
(b)\(\displaystyle 2.81×10^8J\)
(c) 0,36 m/s
(d) Para uma missão de uma semana (168 horas), a mudança na velocidade será de 60 m/s, ou aproximadamente 1%. Em geral, uma diminuição na velocidade faria com que a órbita começasse a espiralar para dentro porque a velocidade não seria mais suficiente para manter a órbita circular. As consequências a longo prazo são que o ônibus espacial precisaria de um pouco mais de combustível para manter a velocidade desejada, caso contrário, a órbita espiralaria ligeiramente para dentro.
23.4 Correntes parasitas e amortecimento magnético
56. Faça um desenho semelhante ao da Figura, mas com o pêndulo se movendo na direção oposta. Em seguida, use a lei de Faraday, a lei de Lenz e a RHR-1 para mostrar que a força magnética se opõe ao movimento.
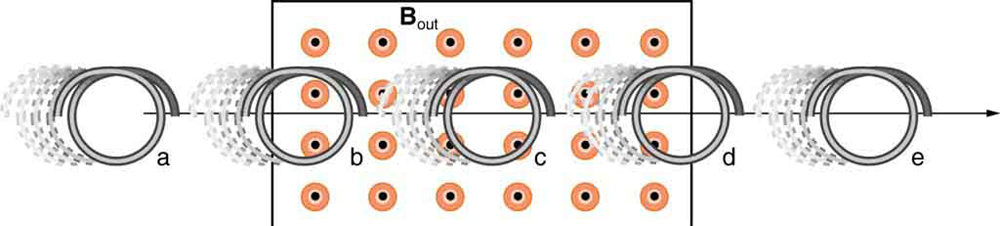
Uma bobina é movida para dentro e para fora de uma região de campo magnético uniforme.
57. Uma bobina é movida através de um campo magnético, conforme mostrado na Figura. O campo é uniforme dentro do retângulo e zero fora. Qual é a direção da corrente induzida e qual é a direção da força magnética na bobina em cada posição mostrada?
23.5 Geradores elétricos
58. Calcule a tensão de pico de um gerador que gira sua bobina de 200 voltas e 0,100 m de diâmetro a 3600 rpm em um campo de 0,800 T.
Solução
474 V
59. Em que velocidade angular em rpm a tensão de pico de um gerador será de 480 V, se sua bobina de 500 voltas e 8,00 cm de diâmetro girar em um campo de 0,250 T?
60. Qual é o pico de emf gerado pela rotação de uma bobina de 1000 voltas e 20,0 cm de diâmetro no campo\(\displaystyle 5.00×10^{−5}T\) magnético da Terra, dado que o plano da bobina é originalmente perpendicular ao campo da Terra e é girado para ficar paralelo ao campo em 10,0 ms?
Solução
0,247 V
61. Qual é o pico de emf gerado por um raio de 0,250 m, a bobina de 500 voltas é girada um quarto de uma revolução em 4,17 ms, originalmente tendo seu plano perpendicular a um campo magnético uniforme. (Isso é 60 rev/s.)
62. (a) Um gerador de bicicleta gira a 1875 rad/s, produzindo um pico emf de 18,0 V. Ele tem uma bobina retangular de 1,00 por 3,00 cm em um campo de 0,640 T. Quantas voltas estão na bobina?
(b) Esse número de voltas de fio é prático para uma bobina de 1,00 por 3,00 cm?
Solução
(a) 50
(b) Sim
63. Conceitos integrados
Esse problema se refere ao gerador de bicicletas considerado no problema anterior. É acionado por uma roda de 1,60 cm de diâmetro que rola na borda externa do pneu da bicicleta.
(a) Qual é a velocidade da bicicleta se a velocidade angular do gerador for 1875 rad/s?
(b) Qual é a emf máxima do gerador quando a bicicleta se move a 10,0 m/s, observando que era 18,0 V nas condições originais?
(c) Se o gerador sofisticado puder variar seu próprio campo magnético, qual intensidade de campo ele precisará em 5,00 m/s para produzir um emf máximo de 9,00 V?
64. (a) Um gerador de carro gira a 400 rpm quando o motor está em marcha lenta. Sua bobina retangular de 300 voltas e 5,00 por 8,00 cm gira em um campo magnético ajustável para que possa produzir tensão suficiente mesmo em baixas rotações. Qual é a intensidade de campo necessária para produzir um pico de EMF de 24,0 V?
(b) Discuta como essa intensidade de campo necessária se compara às disponíveis em ímãs permanentes e eletroímãs.
Solução
(a) 0,477 T
(b) Essa intensidade de campo é pequena o suficiente para ser obtida usando um ímã permanente ou um eletroímã.
65. Mostre que se uma bobina gira em uma velocidade angular\(\displaystyle ω\), o período de sua saída CA é\(\displaystyle 2π/ω\).
66. Uma bobina de 75 voltas e 10,0 cm de diâmetro gira a uma velocidade angular de 8,00 rad/s em um campo de 1,25 T, começando com o plano da bobina paralelo ao campo.
(a) Qual é o pico de emf?
(b) Em que momento o pico de emf é atingido pela primeira vez?
(c) Em que momento o emf é o primeiro a ser mais negativo?
(d) Qual é o período da saída de tensão AC?
Solução
(a) 5,89 V
(b) Em t=0
(c) 0,393 s
(d) 0,785 s
67. (a) Se o emf de uma bobina girando em um campo magnético é zero e aumenta até seu primeiro pico em\(\displaystyle t=0.100ms\), qual é a velocidade angular da bobina?\(\displaystyle t=0\)
(b) Em que momento seu próximo máximo ocorrerá?
(c) Qual é o período da produção?
(d) Quando a saída é o primeiro quarto de seu máximo?
(e) Quando é o próximo quarto de seu máximo?
68. Resultados irracionais
Uma bobina de 500 voltas com uma\(\displaystyle 0.250m^2\) área é girada no\(\displaystyle 5.00×10^{−5}T\) campo da Terra, produzindo uma emf máxima de 12,0 kV.
(a) Em que velocidade angular a bobina deve ser girada?
(b) O que não é razoável nesse resultado?
(c) Qual suposição ou premissa é responsável?
Solução
(a)\(\displaystyle 1.92×10^6rad/s\)
(b) Essa velocidade angular é excessivamente alta, maior do que pode ser obtida para qualquer sistema mecânico.
(c) A suposição de que uma tensão tão alta quanto 12,0 kV poderia ser obtida não é razoável.
23.6 Emf preta
69. Suponha que um motor conectado a uma fonte de 120 V consuma 10,0 A ao iniciar pela primeira vez.
(a) Qual é sua resistência?
(b) Que corrente ele consome em sua velocidade normal de operação quando desenvolve uma emf reversa de 100 V?
Solução
(a) 12,00 Ω
(b) 1,67 A
70. Um motor operando com eletricidade de 240 V tem um emf traseiro de 180 V em velocidade de operação e consome uma corrente de 12,0 A. (a) Qual é sua resistência? (b) Que corrente ele consome quando é iniciado pela primeira vez?
71. Qual é a emf traseira de um motor de 120 V que consome 8,00 A em sua velocidade normal e 20,0 A na primeira partida?
Solução
72,0 V
72. O motor de um carro de brinquedo opera em 6,00 V, desenvolvendo um emf traseiro de 4,50 V em velocidade normal. Se ele extrai 3,00 A na velocidade normal, que corrente ele consome ao iniciar?
73. Conceitos integrados
O motor de um carro de brinquedo é alimentado por quatro baterias em série, que produzem uma emf total de 6,00 V. O motor consome 3,00 A e desenvolve uma emf traseira de 4,50 V em velocidade normal. Cada bateria tem uma resistência\(\displaystyle 0.100 Ω\) interna. Qual é a resistência do motor?
Solução
0,100 Ω
23.7 Transformadores
74. Um transformador plug-in, como o da Figura, fornece 9,00 V a um sistema de videogame.
(a) Quantas voltas existem em sua bobina secundária, se sua tensão de entrada é de 120 V e a bobina primária tem 400 voltas?
(b) Qual é sua corrente de entrada quando sua saída é 1,30 A?
Solução
(a) 30.0
(b)\(\displaystyle 9.75×10^{−2}A\)
75. Uma viajante americana na Nova Zelândia carrega um transformador para converter o padrão de 240 V da Nova Zelândia em 120 V para que ela possa usar alguns pequenos eletrodomésticos em sua viagem.
(a) Qual é a proporção de voltas nas bobinas primária e secundária de seu transformador?
(b) Qual é a relação entre a corrente de entrada e saída?
(c) Como uma neozelandesa viajando pelos Estados Unidos poderia usar esse mesmo transformador para alimentar seus aparelhos de 240 V a partir de 120 V?
76. Um gravador de cassete usa um transformador plug-in para converter 120 V em 12,0 V, com uma saída de corrente máxima de 200 mA.
(a) Qual é a entrada atual?
(b) Qual é a entrada de energia?
(c) Essa quantidade de energia é razoável para um pequeno eletrodoméstico?
Solução
(a) 20,0 mA
(b) 2,40 W
(c) Sim, essa quantidade de energia é bastante razoável para um aparelho pequeno.
77. (a) Qual é a tensão de saída de um transformador usado para baterias de lanternas recarregáveis, se o primário tem 500 voltas, o secundário 4 voltas e a tensão de entrada é 120 V?
(b) Qual corrente de entrada é necessária para produzir uma saída de 4,00 A? (c) Qual é a entrada de energia?
78. (a) O transformador plug-in de um laptop produz 7,50 V e pode fornecer uma corrente máxima de 2,00 A. Qual é a corrente máxima de entrada se a tensão de entrada for 240 V? Suponha 100% de eficiência.
(b) Se a eficiência real for inferior a 100%, a corrente de entrada precisaria ser maior ou menor? Explique.
Solução
(a) 0,063 A
(b) Maior corrente de entrada necessária.
79. Um transformador multiuso tem uma bobina secundária com vários pontos nos quais uma tensão pode ser extraída, fornecendo saídas de 5,60, 12,0 e 480 V.
(a) A tensão de entrada é de 240 V para uma bobina primária de 280 voltas. Quais são os números de voltas nas partes do secundário usadas para produzir as tensões de saída?
(b) Se a corrente máxima de entrada for 5,00 A, quais são as correntes máximas de saída (cada uma usada sozinha)?
80. Uma grande usina gera eletricidade a 12,0 kV. Seu antigo transformador já converteu a tensão em 335 kV. O secundário desse transformador está sendo substituído para que sua saída possa ser de 750 kV para uma transmissão mais eficiente entre países em linhas de transmissão atualizadas.
(a) Qual é a proporção de voltas no novo secundário em comparação com o secundário antigo?
(b) Qual é a relação entre a nova saída de corrente e a saída antiga (a 335 kV) para a mesma potência?
(c) Se as linhas de transmissão atualizadas tiverem a mesma resistência, qual é a relação entre a perda de energia da nova linha e a antiga?
Solução
(a) 2,2
(b) 0,45
(c) 0,20 ou 20,0%
81. Se a potência no problema anterior for de 1000 MW e a resistência da linha for\(\displaystyle 2.00 Ω\), quais foram as perdas da linha antiga e da nova?
82. Resultados irracionais
A eletricidade de 335 kV AC de uma linha de transmissão de energia é alimentada na bobina primária de um transformador. A proporção entre o número de voltas no secundário e o número no primário é\(\displaystyle N_s/N_p=1000\).
(a) Qual tensão é induzida no secundário?
(b) O que não é razoável nesse resultado?
(c) Qual suposição ou premissa é responsável?
Solução
(a) 335 MV
(b) muito alta, muito além da tensão de ruptura do ar em distâncias razoáveis
(c) a tensão de entrada é muito alta
83. Construa seu próprio problema
Considere um transformador duplo a ser usado para criar voltagens muito grandes. O dispositivo consiste em dois estágios. O primeiro é um transformador que produz uma tensão de saída muito maior do que sua entrada. A saída do primeiro transformador é usada como entrada para um segundo transformador que aumenta ainda mais a tensão. Crie um problema no qual você calcule a tensão de saída do estágio final com base na tensão de entrada do primeiro estágio e no número de voltas ou voltas em ambas as partes dos dois transformadores (quatro bobinas ao todo). Calcule também a corrente máxima de saída do estágio final com base na corrente de entrada. Discuta a possibilidade de perdas de energia nos dispositivos e o efeito na corrente e na potência de saída.
23.8 Segurança elétrica: sistemas e dispositivos
84. Conceitos integrados
Um curto-circuito na caixa metálica aterrada de um aparelho ocorre conforme mostrado na Figura. A pessoa que toca na capa está molhada e só tem\(\displaystyle 3.00 kΩ\) resistência à terra/terra.
(a) Qual é a voltagem na caixa se 5,00 mA fluir pela pessoa?
(b) Qual é a corrente no curto-circuito se a resistência do fio de terra/terra for\(\displaystyle 0.200 Ω\)?
(c) Isso acionará o disjuntor de 20,0 A que abastece o aparelho?
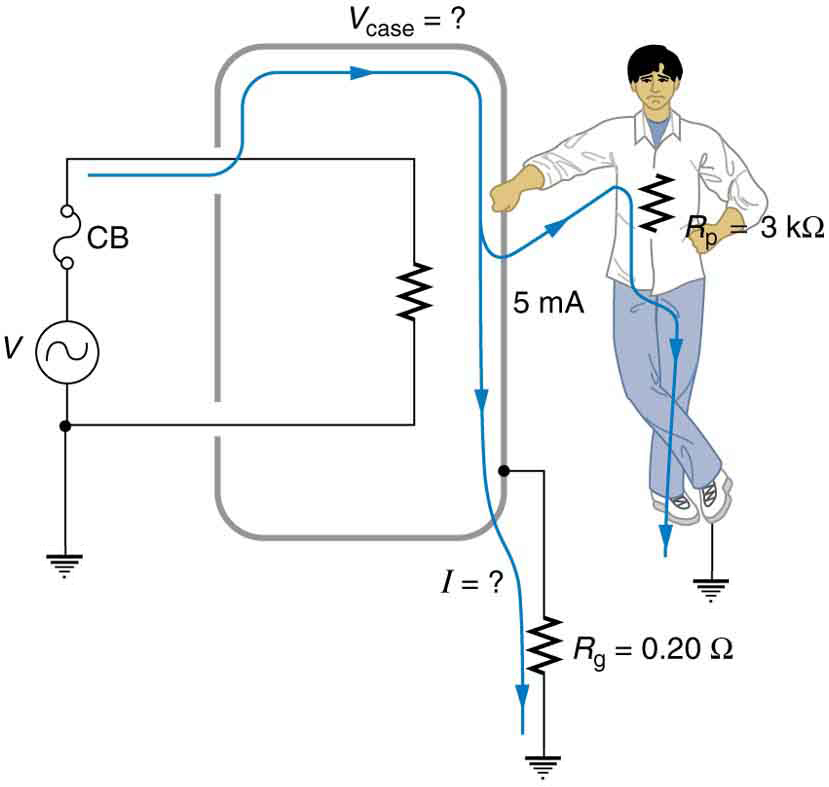
Uma pessoa pode ficar chocada mesmo quando a caixa de um aparelho está aterrada. A grande corrente de curto-circuito produz uma tensão na caixa do aparelho, pois a resistência do fio de terra/terra não é zero.
Solução
(a) 15,0 V
(b) 75,0 A
(c) sim
23.9 Indutância
85. Duas bobinas são colocadas juntas em um laboratório de física para demonstrar a lei de indução de Faraday. Uma corrente de 5,00 A em um é desligada em 1,00 ms, induzindo um emf de 9,00 V no outro. Qual é a indutância mútua deles?
Solução
1,80 mH
86. Se duas bobinas colocadas uma ao lado da outra tiverem uma indutância mútua de 5,00 mH, qual voltagem é induzida em uma quando a corrente de 2,00 A na outra é desligada em 30,0 ms?
87. A corrente de 4,00 A através de um indutor de 7,50 mH é desligada em 8,33 ms. O que é o emf induzido em oposição a isso?
Solução
3,60 V
88. Um dispositivo é ligado e 3,00 A passa por ele 0,100 ms depois. Qual é a autoindutância do dispositivo se um emf induzido de 150 V se opõe a isso?
89. Começando com\(\displaystyle emf_2=−M\frac{ΔI_1}{Δt}\), mostre que as unidades de indutância são\(\displaystyle (V⋅s)/A=Ω⋅s\).
90. Os flashes da câmera carregam um capacitor em alta tensão ligando e desligando rapidamente a corrente por meio de um indutor. Em que tempo a corrente de 0,100 A através de um indutor de 2,00 mH deve ser ligada ou desligada para induzir um emf de 500 V?
91. Um grande solenóide de pesquisa tem uma autoindutância de 25,0 H.
(a) Qual emf induzido se opõe a desligá-lo quando 100 A de corrente através dele são desligados em 80,0 ms?
(b) Quanta energia é armazenada no indutor em plena corrente?
(c) Em que taxa em watts a energia deve ser dissipada para desligar a corrente em 80,0 ms?
(d) Tendo em vista a resposta à última parte, é surpreendente que fechá-la tão rapidamente seja difícil?
Solução
(a) 31,3 kV
(b) 125 kJ
(c) 1,56 MW
(d) Não, não é surpreendente, pois essa potência é muito alta.
92. (a) Calcule a autoindutância de um solenóide de 50,0 cm de comprimento e 10,0 cm de diâmetro com 1000 voltas.
(b) Quanta energia é armazenada neste indutor quando 20,0 A de corrente flui através dele?
(c) Com que rapidez ele pode ser desligado se o emf induzido não exceder 3,00 V?
93. Um resistor de laboratório de precisão é feito de uma bobina de fio de 1,50 cm de diâmetro e 4,00 cm de comprimento e tem 500 voltas.
(a) Qual é sua autoindutância?
(b) Que média de emf é induzida se a corrente de 12,0 A através dela for ligada em 5,00 ms (um quarto de um ciclo para 50 Hz AC)?
(c) Qual é sua indutância se for encurtada para metade de seu comprimento e contra-enrolada (duas camadas de 250 voltas em direções opostas)?
Solução
(a) 1,39 mH
(b) 3,33 V
(c) Zero
94. As bobinas de aquecimento em um secador de cabelo têm 0,800 cm de diâmetro, têm um comprimento combinado de 1,00 m e um total de 400 voltas.
(a) Qual é sua autoindutância total, supondo que eles ajam como um único solenóide?
(b) Quanta energia é armazenada neles quando 6,00 A flui?
(c) Que média de emf se opõe a desligá-los se isso for feito em 5,00 ms (um quarto de um ciclo para 50 Hz AC)?
95. Quando a corrente de 20,0 A através de um indutor é desligada em 1,50 ms, um emf de 800 V é induzido, opondo-se à mudança. Qual é o valor da autoindutância?
Solução
60,0 mH
96. Com que rapidez a corrente de 150 A através de um indutor de 0,250 H pode ser desligada se o emf induzido não puder exceder 75,0 V?
97. Conceitos integrados
Um solenóide supercondutor muito grande, como o usado em exames de ressonância magnética, armazena 1,00 MJ de energia em seu campo magnético quando 100 A flui.
(a) Encontre sua autoindutância.
(b) Se as bobinas “ficarem normais”, elas ganham resistência e começam a dissipar a energia térmica. Qual aumento de temperatura é produzido se toda a energia armazenada for usada para aquecer o ímã de 1000 kg, considerando seu calor específico médio\(\displaystyle 200 J/kg⋅ºC\)?
Solução
(a) 200 H
(b) 5,00ºC
98. Resultados irracionais
Um indutor de 25,0 H tem 100 A de corrente desligada em 1,00 ms.
(a) Que voltagem é induzida para se opor a isso?
(b) O que não é razoável nesse resultado?
(c) Qual suposição ou premissa é responsável?
Circuitos RL 23.10
99. Se você quiser uma constante de\(\displaystyle RL\) tempo característica de 1,00 s e tiver um resistor de 500 Ω, qual valor de autoindutância é necessário?
Solução
500 H
100. Seu\(\displaystyle RL\) circuito tem uma constante de tempo característica de 20,0 ns e uma resistência de\(\displaystyle 5.00 MΩ\).
(a) Qual é a indutância do circuito?
(b) Que resistência lhe daria uma constante de tempo de 1,00 ns, talvez necessária para uma resposta rápida em um osciloscópio?
101. Um grande ímã supercondutor, usado para ressonância magnética, tem uma indutância de 50,0 H. Se você quiser que a corrente que passa por ela seja ajustável com uma constante de tempo característica de 1,00 s, qual é a resistência mínima do sistema?
Solução
50,0 Ω
102. Verifique se após um tempo de 10,0 ms, a corrente para a situação considerada no Exemplo será 0,183 A, conforme declarado.
103. Suponha que você tenha um suprimento de indutores variando de 1,00 nH a 10,0 H e resistores variando\(\displaystyle 0.100Ω\) de\(\displaystyle 1.00MΩ\) a. Qual é a faixa de constantes de\(\displaystyle RL\) tempo características que você pode produzir conectando um único resistor a um único indutor?
Solução
\(\displaystyle 1.00×10^{–18}s\) para 0,100 s
104. (a) Qual é a constante de tempo característica de um indutor de 25,0 mH que tem uma resistência de\(\displaystyle 4.00Ω\)?
(b) Se estiver conectado a uma bateria de 12,0 V, qual é a corrente após 12,5 ms?
105. Qual porcentagem da corrente final\(\displaystyle I_0\) flui através de um indutor\(\displaystyle L\) em série com um resistor\(\displaystyle R\), três constantes de tempo após a conclusão do circuito?
Solução
95,0%
106. A corrente de 5,00 A através de um indutor de 1,50 H é dissipada por um\(\displaystyle 2.00 Ω\) resistor em um circuito como o da Figura com o interruptor na posição 2.
(a) Qual é a energia inicial no indutor?
(b) Quanto tempo a corrente levará para cair para 5,00% de seu valor inicial?
(c) Calcule a potência média dissipada e compare-a com a potência inicial dissipada pelo resistor.
107. (a) Use o tratamento exponencial exato para descobrir quanto tempo é necessário para levar a corrente a um indutor de 80,0 mH em série com um\(\displaystyle 15.0 Ω\) resistor a 99,0% de seu valor final, começando do zero.
(b) Compare sua resposta com o tratamento aproximado usando números integrais de λ.
(c) Discuta o quão significativa é a diferença.
Solução
(a) 24,6 ms
(b) 26,7 ms
(c) 9% de diferença, que é maior do que a incerteza inerente aos parâmetros fornecidos.
108. (a) Usando o tratamento exponencial exato, encontre o tempo necessário para que a corrente por meio de um indutor de 2,00 H em série com um resistor de 0,500 Ω seja reduzido para 0,10% de seu valor original.
(b) Compare sua resposta com o tratamento aproximado usando números integrais de\(\displaystyle τ\).
(c) Discuta o quão significativa é a diferença.
23.11 Reatância, indutiva e capacitiva
109. Em que frequência um indutor de 30,0 mH terá uma reatância de 100 Ω?
Solução
531 Hz
110. Qual valor de indutância deve ser usado se uma\(\displaystyle 20.0 kΩ\) reatância for necessária na frequência de 500 Hz?
111. Qual capacitância deve ser usada para produzir uma\(\displaystyle 2.00 MΩ\) reatância a 60,0 Hz?
Solução
1,33 nF
112. Em que frequência um capacitor de 80,0 mF terá uma reatância de\(\displaystyle 0.250 Ω\)?
113. (a) Encontre a corrente por meio de um indutor de 0,500 H conectado a uma fonte CA de 60,0 Hz e 480 V.
(b) Qual seria a corrente em 100 kHz?
Solução
(a) 2,55 A
(b) 1,53 mA
114. (a) Que corrente flui quando uma fonte CA de 60,0 Hz e 480 V é conectada a um capacitor de 0,250 μF?
(b) Qual seria a corrente em 25,0 kHz?
115. Uma fonte de 20,0 kHz e 16,0 V conectada a um indutor produz uma corrente de 2,00 A. O que é a indutância?
Solução
63,7 µH
116. Uma fonte de 20,0 Hz e 16,0 V produz uma corrente de 2,00 mA quando conectada a um capacitor. Qual é a capacitância?
117. (a) Um indutor projetado para filtrar o ruído de alta frequência da energia fornecida a um computador pessoal é colocado em série com o computador. Qual indutância mínima ela deve ter para produzir uma\(\displaystyle 2.00 kΩ\) reatância para ruído de 15,0 kHz?
(b) Qual é sua reatância a 60,0 Hz?
Solução
(a) 21,2 mH
(b) 8,00 Ω
118. O capacitor na Figura (a) foi projetado para filtrar sinais de baixa frequência, impedindo sua transmissão entre circuitos.
(a) Qual capacitância é necessária para produzir uma\(\displaystyle 100 kΩ\) reatância na frequência de 120 Hz?
(b) Qual seria sua reatância em 1,00 MHz?
(c) Discuta as implicações de suas respostas a (a) e (b).
119. O capacitor na Figura (b) filtrará os sinais de alta frequência encurtando-os para a terra/terra.
(a) Qual capacitância é necessária para produzir uma reatância de\(\displaystyle 10.0 mΩ\) para um sinal de 5,00 kHz?
(b) Qual seria sua reatância em 3,00 Hz? (c) Discuta as implicações de suas respostas a (a) e (b).
Solução
(a) 3,18 mF
(b) 16,7 Ω
120. Resultados irracionais
Em um registro de voltagens devido à atividade cerebral (um EEG), um sinal de 10,0 mV com frequência de 0,500 Hz é aplicado a um capacitor, produzindo uma corrente de 100 mA. A resistência é insignificante.
(a) Qual é a capacitância?
(b) O que não é razoável nesse resultado?
(c) Qual suposição ou premissa é responsável?
121. Construa seu próprio problema
Considere o uso de um indutor em série com um computador operando com eletricidade de 60 Hz. Crie um problema no qual você calcule a redução relativa na tensão do ruído de alta frequência de entrada em comparação com a tensão de 60 Hz. Entre as coisas a considerar estão a reatância em série aceitável do indutor para potência de 60 Hz e as prováveis frequências de ruído que passam pelas linhas de energia.
23.12 Circuitos AC da série RLC
122. Um\(\displaystyle RL\) circuito consiste em um\(\displaystyle 40.0 Ω\) resistor e um indutor de 3,00 mH.
(a) Encontre sua impedância\(\displaystyle Z\) em 60,0 Hz e 10,0 kHz.
(b) Compare esses valores\(\displaystyle Z\) com aqueles encontrados no Exemplo em que também havia um capacitor.
Solução
(a)\(\displaystyle 40.02 Ω\) a 60,0 Hz,\(\displaystyle 193 Ω\) a 10,0 kHz
(b) A 60 Hz, com um capacitor\(\displaystyle Z=531 Ω\), mais de 13 vezes mais alta do que sem o capacitor. O capacitor faz uma grande diferença em baixas frequências. A 10 kHz, com um capacitor\(\displaystyle Z=190 Ω\), quase o mesmo que sem o capacitor. O capacitor tem um efeito menor em altas frequências.
123. Um\(\displaystyle RC\) circuito consiste em um\(\displaystyle 40.0 Ω\) resistor e um\(\displaystyle 5.00 μF\) capacitor.
(a) Encontre sua impedância em 60,0 Hz e 10,0 kHz.
(b) Compare esses valores\(\displaystyle Z\) com aqueles encontrados no Exemplo, no qual também havia um indutor.
124. Um\(\displaystyle C \) circuito consiste em um\(\displaystyle 3.00mH\) indutor e um\(\displaystyle 5.00μF\) capacitor.
(a) Encontre sua impedância em 60,0 Hz e 10,0 kHz.
(b) Compare esses valores\(\displaystyle Z\) com aqueles encontrados no Exemplo em que também havia um resistor.
Solução
(a)\(\displaystyle 529 Ω\) a 60,0 Hz,\(\displaystyle 185 Ω\) a 10,0 kHz
(b) Esses valores são próximos aos obtidos no Exemplo porque em baixa frequência o capacitor domina e em alta frequência o indutor domina. Portanto, em ambos os casos, o resistor faz pouca contribuição para a impedância total.
125. Qual é a frequência de ressonância de um indutor de 0,500 mH conectado a um\(\displaystyle 40.0 μF\) capacitor?
126. Para receber rádio AM, você quer um\(\displaystyle RLC\) circuito que possa ressoar em qualquer frequência entre 500 e 1650 kHz. Isso é feito com um\(\displaystyle 1.00 μH\) indutor fixo conectado a um capacitor variável. Qual faixa de capacitância é necessária?
Solução
9,30 nF a 101 nF
127. Suponha que você tenha um suprimento de indutores variando de 1,00 nH a 10,0 H e capacitores variando de 1,00 pF a 0,100 F. Qual é a faixa de frequências ressonantes que pode ser alcançada a partir de combinações de um único indutor e um único capacitor?
128. Qual capacitância você precisa para produzir uma frequência ressonante de 1,00 GHz, ao usar um indutor de 8,00 nH?
Solução
3.17 pF
129. Qual indutância você precisa para produzir uma frequência ressonante de 60,0 Hz ao usar um\(\displaystyle 2.00 μF\) capacitor?
130. A frequência mais baixa na banda de rádio FM é 88,0 MHz.
(a) Qual indutância é necessária para produzir essa frequência ressonante se ela estiver conectada a um capacitor de 2,50 pF?
(b) O capacitor é variável, para permitir que a frequência de ressonância seja ajustada para até 108 MHz. Qual deve ser a capacitância nessa frequência?
Solução
(a)\(\displaystyle 1.31 μH\)
(b)\(\displaystyle 1.66 pF\)
131. Um circuito em\(\displaystyle RLC\) série tem um\(\displaystyle 2.50 Ω\) resistor, um\(\displaystyle 100 μH\) indutor e um\(\displaystyle 80.0 μF\) capacitor.
(a) Encontre a impedância do circuito em 120 Hz.
(b) Encontre a impedância do circuito em 5,00 kHz.
(c) Se a fonte de tensão tiver\(\displaystyle V_{rms}=5.60V\), o que há\(\displaystyle I_{rms}\) em cada frequência?
(d) Qual é a frequência de ressonância do circuito?
(e) O que está\(\displaystyle I_{rms}\) em ressonância?
132. Um circuito em\(\displaystyle RLC\) série tem um\(\displaystyle 1.00 kΩ\) resistor, um\(\displaystyle 150 μH\) indutor e um capacitor de 25,0 nF.
(a) Encontre a impedância do circuito em 500 Hz.
(b) Encontre a impedância do circuito em 7,50 kHz.
(c) Se a fonte de tensão tiver\(\displaystyle V_{rms}=408V\), o que há\(\displaystyle I_{rms}\) em cada frequência?
(d) Qual é a frequência de ressonância do circuito?
(e) O que está\(\displaystyle I_{rms}\) em ressonância?
Solução
(a) 12,8 kΩ
(b) 1,31 kΩ
(c) 31,9 mA a 500 Hz, 312 mA a 7,50 kHz
(d) 82,2 kHz
(e) 0,408 A
133. Um circuito em\(\displaystyle RLC\) série tem um\(\displaystyle 2.50 Ω\) resistor, um\(\displaystyle 100 μH\) indutor e um\(\displaystyle 80.0 μF\) capacitor.
(a) Encontre o fator de potência em f = 120 Hz.
(b) Qual é o ângulo de fase em 120 Hz?
(c) Qual é a potência média em 120 Hz?
(d) Encontre a potência média na frequência ressonante do circuito.
134. Um circuito em\(\displaystyle RLC\) série tem um\(\displaystyle 1.00 kΩ\) resistor, um\(\displaystyle 150 μH\) indutor e um capacitor de 25,0 nF
(a) Encontre o fator de potência em f = 7,50 Hz.
(b) Qual é o ângulo de fase nessa frequência?
(c) Qual é a potência média nessa frequência?
(d) Encontre a potência média na frequência ressonante do circuito.
Solução
(a) 0,159
(b) 80,9º
(c) 26,4 W
(d) 166 W
135. Um circuito em\(\displaystyle RLC\) série tem um\(\displaystyle 200 Ω\) resistor e um indutor de 25,0 mH. Em 8000 Hz, o ângulo de fase é\(\displaystyle 45.0º\).
(a) Qual é a impedância?
(b) Encontre a capacitância do circuito.
(c) Se\(\displaystyle V_{rms}=408V\) for aplicada, qual é a potência média fornecida?
136. Referindo-se ao exemplo, encontre a potência média em 10,0 kHz.
Solução
16,0 W

