23.12: Indutância

Last updated
Save as PDF

Page ID: 194998

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Calcule a indutância de um indutor.
Calcule a energia armazenada em um indutor.
Calcule o emf gerado em um indutor.

Indutores

A indução é o processo no qual um emf é induzido pela alteração do fluxo magnético. Muitos exemplos foram discutidos até agora, alguns mais eficazes do que outros. Os transformadores, por exemplo, são projetados para serem particularmente eficazes na indução da tensão e da corrente desejadas com pouquíssima perda de energia para outras formas. Existe uma quantidade física útil relacionada à “eficácia” de um determinado dispositivo? A resposta é sim, e essa quantidade física é chamada de indutância.

A indutância mútua é o efeito da lei de indução de Faraday de um dispositivo sobre outro, como a bobina primária na transmissão de energia para o secundário em um transformador. Veja a Figura, onde bobinas simples induzem EMFS umas nas outras.

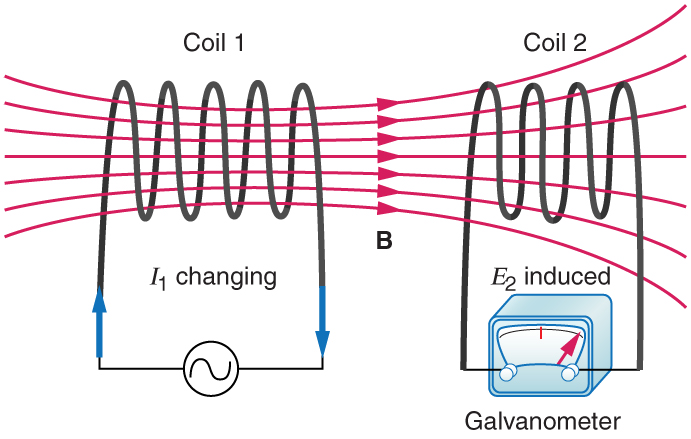
A figura mostra duas bobinas, a bobina uma, de cinco voltas e a bobina duas, de quatro voltas, mantidas adjacentes uma à outra. É mostrado que as linhas do campo magnético de força B passam pelas duas bobinas. É mostrado que a bobina um está conectada a uma fonte A C. A corrente variável na bobina é dada como I no sentido horário. A bobina dois está conectada a um galvanômetro. É mostrado que uma mudança na corrente na bobina um induz um e m f na bobina dois. O e m f induzido na bobina dois é medido como uma deflexão no galvanômetro. — Figura\(\PageIndex{1}\): Essas bobinas podem induzir EMFS umas nas outras, como um transformador ineficiente. Sua indutância mútua M indica a eficácia do acoplamento entre eles. Aqui, uma mudança na corrente na bobina 1 induz um emf na bobina 2. (Observe que “\(E_2\)induzido” representa o emf induzido na bobina 2.)

Nos muitos casos em que a geometria dos dispositivos é fixa, o fluxo é alterado pela variação da corrente. Portanto, nos concentramos na taxa de mudança da corrente\(\Delta I/\delta t\), como causa da indução. Uma mudança na corrente\(I_1\) em um dispositivo, a bobina 1 na figura, induz uma\(I_2\) no outro. Expressamos isso em forma de equação como

\[emf_2 = - M\dfrac{\Delta I_1}{\Delta t},\]onde\(M\) é definido como sendo a indutância mútua entre os dois dispositivos. O sinal negativo é uma expressão da lei de Lenz. Quanto maior a indutância mútua\(M\), mais eficaz é o acoplamento. Por exemplo, as bobinas na Figura têm um tamanho pequeno\(M\) em comparação com as bobinas do transformador em [link]. As unidades para\(M\) são (V\ cdot s) /A =\ Omega\ cdot s\), que é chamado de henry (H), em homenagem a Joseph Henry. Isso é,\(1 \, H = 1 \, \Omega \cdot s\).

A natureza é simétrica aqui. Se mudarmos a corrente\(I_2\) na bobina 2, induzimos uma\(emf_1\) na bobina 1, que é dada por

\[emf_1 = -M \dfrac{\Delta I_2}{\Delta t},\]onde\(M\) é o mesmo que para o processo inverso. Os transformadores funcionam para trás com a mesma eficácia ou indutância mútua\(M\).

Uma grande indutância mútua\(M\) pode ou não ser desejável. Queremos que um transformador tenha uma grande indutância mútua. Mas um aparelho, como uma secadora de roupas elétrica, pode induzir um emf perigoso em sua caixa se a indutância mútua entre as bobinas e a caixa for grande. Uma forma de reduzir a indutância mútua\(M\) é contrabalançar as bobinas para cancelar o campo magnético produzido. (Veja a Figura.)

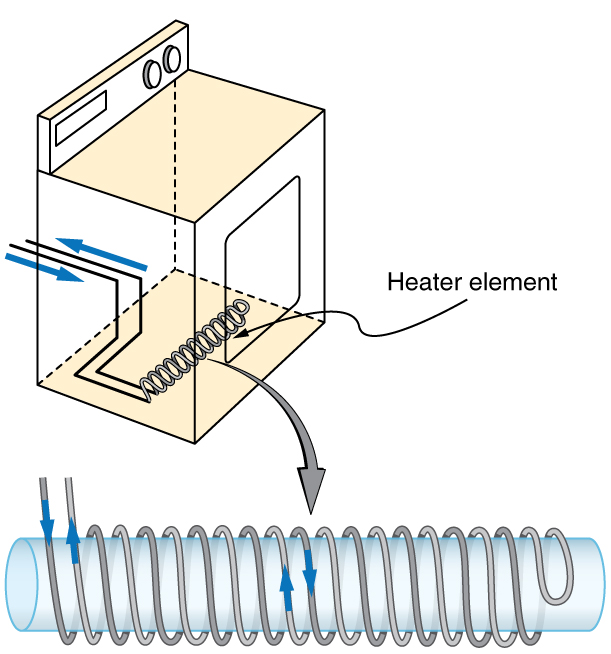
A figura descreve as bobinas de aquecimento da secadora de roupas elétrica que são enroladas em um núcleo cilíndrico. Lá, os campos magnéticos se cancelam. — Figura\(\PageIndex{2}\): As bobinas de aquecimento de uma secadora de roupas elétrica podem ser contrabalançadas para que seus campos magnéticos se cancelem, reduzindo consideravelmente a indutância mútua com a caixa da secadora.

A autoindutância, o efeito da lei de Faraday de indução de um dispositivo sobre si mesmo, também existe. Quando, por exemplo, a corrente através de uma bobina é aumentada, o campo magnético e o fluxo também aumentam, induzindo um contra-emf, conforme exigido pela lei de Lenz. Por outro lado, se a corrente for diminuída, um emf é induzido que se opõe à diminuição. A maioria dos dispositivos tem uma geometria fixa e, portanto, a mudança no fluxo se deve inteiramente à mudança na corrente\(\Delta I\) através do dispositivo. O emf induzido está relacionado à geometria física do dispositivo e à taxa de variação da corrente. É dado por

\[emf = -L \dfrac{\Delta I}{\Delta t},\]onde\(L\) está a autoindutância do dispositivo. Um dispositivo que apresenta autoindutância significativa é chamado de indutor e recebe o símbolo na Figura.

Duas linhas retas conectadas por três semicírculos adjacentes uma à outra. — Figura\(\PageIndex{3}\):

O sinal de menos é uma expressão da lei de Lenz, indicando que a emf se opõe à mudança na corrente. As unidades de autoindutância são henries (H), assim como a indutância mútua. Quanto maior a autoindutância\(L\) de um dispositivo, maior sua oposição a qualquer mudança na corrente através dele. Por exemplo, uma bobina grande com muitas voltas e um núcleo de ferro tem uma bobina grande\(L\) e não permite que a corrente mude rapidamente. Para evitar esse efeito, um pequeno\(L\) deve ser alcançado, como por exemplo, enrolando bobinas, como na Figura 1.

Um indutor de 1 H é um indutor grande. Para ilustrar isso, considere um dispositivo com\(L = 1.0 \, H\) uma corrente de 10 A fluindo através dele. O que acontece se tentarmos desligar a corrente rapidamente, talvez em apenas 1,0 ms? Um emf, dado por\(emf = -L(\Delta I/\Delta t)\), se oporá à mudança. Assim, um emf será induzido dado por\(emf = -L(\Delta I/\Delta t) = (1.0 \, H)[(10 \, A)/(1.0 \, ms)] = 10,000 \, V\). O sinal positivo significa que essa grande tensão está na mesma direção da corrente, opondo-se à sua diminuição. Esses emfs grandes podem causar arcos, danificar o equipamento de comutação e, portanto, pode ser necessário mudar a corrente mais lentamente.

Existem usos para uma tensão induzida tão grande. Os flashes da câmera usam uma bateria, dois indutores que funcionam como um transformador e um sistema de comutação ou oscilador para induzir grandes tensões. (Lembre-se de que precisamos de um campo magnético variável, provocado por uma mudança de corrente, para induzir uma tensão em outra bobina.) O sistema oscilador fará isso muitas vezes, pois a voltagem da bateria é aumentada para mais de mil volts. (Você pode ouvir o zumbido agudo do transformador enquanto o capacitor está sendo carregado.) Um capacitor armazena a alta voltagem para uso posterior na alimentação do flash. (Veja a Figura.)

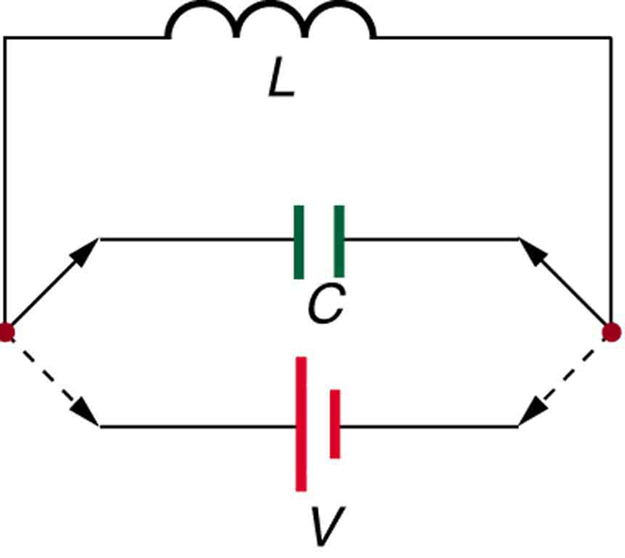
A figura descreve um indutor L que é conectado em paralelo a um capacitor C por meio de uma chave variável. Há uma célula de tensão V colocada paralelamente ao capacitor. As extremidades do interruptor podem ser removidas do capacitor e conectadas à célula V para carregamento. Essa conexão variável é mostrada como setas tracejadas. — Figura\(\PageIndex{4}\): Através da troca rápida de um indutor, baterias de 1,5 V podem ser usadas para induzir emfs de vários milhares de volts. Essa voltagem pode ser usada para armazenar carga em um capacitor para uso posterior, como em um acessório de flash de câmera.

É possível calcular\(L\) para um indutor dada sua geometria (tamanho e forma) e conhecendo o campo magnético que ele produz. Isso é difícil na maioria dos casos, devido à complexidade do campo criado. Portanto, neste texto, a indutância geralmente\(L\) é uma determinada quantidade. Uma exceção é o solenóide, porque tem um campo muito uniforme no interior, um campo quase zero no exterior e uma forma simples. É instrutivo derivar uma equação para sua indutância. Começamos observando que o emf induzido é dado pela lei de indução de Faraday como\(emf = -N(\Delta \Phi /\Delta t)\) e, pela definição de autoindutância, como\(emf = -L(\Delta I/\Delta t)\). Igualando esses rendimentos

\[emf = -N\dfrac{\Delta \Phi}{\Delta t} = -L \dfrac{\Delta I}{\Delta t}.\]

Resolvendo\(L\) doações\[L = N\dfrac{\Delta \Phi}{\Delta I}.\]

Essa equação para a autoindutância\(L\) de um dispositivo é sempre válida. Isso significa que a autoindutância\(L\) depende da eficácia da corrente na criação de fluxo; quanto mais eficaz, maior\(\Delta \phi /\Delta I\) é.

Vamos usar essa última equação para encontrar uma expressão para a indutância de um solenóide. Como a área\(A\) de um solenóide é fixa, a mudança no fluxo é\(\Delta \Phi = \Delta (BA) = A\Delta B\). Para descobrir\(\Delta B\), notamos que o campo magnético de um solenóide é dado por\(B = \mu_0 n I = \mu_0 \frac{\Delta I}{l}\). (Aqui\(n = N/l\), onde\(N\) está o número de bobinas e o comprimento do solenóide.) Somente as mudanças atuais, de modo que\(\Delta \Phi = A \delta B= \mu_0 NA \frac{\Delta I}{l}\). Substituindo\(\Delta \Phi\) em\(L = N \frac{\Delta \Phi}{\Delta I}\) doações

\[L = N\dfrac{\Delta \Phi}{\Delta I} = N \dfrac{\mu_0 NA \frac{\Delta I}{l}}{\Delta I}.\]

Isso simplifica para\[L = \dfrac{\mu_0 N^2 A}{l} (solenoid).\]

Essa é a autoindutância de um solenóide de área\(A\) e comprimento da seção transversal\(l\). Observe que a indutância depende apenas das características físicas do solenóide, consistentes com sua definição.

Exemplo\(\PageIndex{1}\): Calculating the Self-inductance of a Moderate Size Solenoid

Calcule a autoindutância de um solenóide de 10,0 cm de comprimento e 4,00 cm de diâmetro que tem 200 bobinas.

Estratégia

Esta é uma aplicação direta de\(L = \frac{\mu_0 N^2 A}{l}\), uma vez que todas as quantidades na equação, exceto\(L\) são conhecidas.

Solução

Use a seguinte expressão para a autoindutância de um solenóide:

\[L = \dfrac{\mu_0 N^2 A}{l}.\]

A área da seção transversal neste exemplo é\(A = \pi r^2 = (3.14...)(0.0200 \, m)^2 = 1.26 \times 10^{-3} \, m^2\),\(N\) é dada como 200 e o comprimento\(l\) é 0,100 m. Sabemos que a permeabilidade do espaço livre é\(\mu_0 = 4\pi \times 10^{-7} \, T \cdot m/A\). Substituindo-os na expressão “\(L\)dá”

\[L = \dfrac{(4\pi \times 10^{-7} \, T \cdot m/A)(200)^2(1.26 \times 10^{-3} \, m^2)}{0.100 \, m}\]

\[= 0.632 \, mH.\]

Discussão

Este solenóide é de tamanho moderado. Sua indutância de quase um milihenry também é considerada moderada.

Uma aplicação comum de indutância é usada em semáforos que podem dizer quando os veículos estão esperando no cruzamento. Um circuito elétrico com um indutor é colocado na estrada, sob o local onde um carro em espera vai parar. A carroceria do carro aumenta a indutância e o circuito muda enviando um sinal para os semáforos para mudar de cor. Da mesma forma, os detectores de metais usados para a segurança do aeroporto empregam a mesma técnica. Uma bobina ou indutor na estrutura do detector de metais atua tanto como transmissor quanto como receptor. O sinal pulsado na bobina do transmissor induz um sinal no receptor. A autoindutância do circuito é afetada por qualquer objeto metálico no caminho. Esses detectores podem ser ajustados quanto à sensibilidade e também podem indicar a localização aproximada do metal encontrado em uma pessoa. (Mas eles não conseguirão detectar nenhum explosivo plástico como o encontrado no “bombardeiro de roupas íntimas”.) Veja a Figura.

Fotografia de pessoas ao redor de um portão de segurança no terminal de embarque do aeroporto. — Figura\(\PageIndex{5}\): O conhecido portão de segurança de um aeroporto pode não apenas detectar metais, mas também indicar sua altura aproximada acima do piso. (crédito: Alexburds, Wikimedia Commons)

Energia armazenada em um indutor

Sabemos pela lei de Lenz que as indutâncias se opõem às mudanças atuais. Existe uma forma alternativa de olhar para essa oposição que é baseada na energia. A energia é armazenada em um campo magnético. É preciso tempo para acumular energia e também para esgotar a energia; portanto, há uma oposição à mudança rápida. Em um indutor, o campo magnético é diretamente proporcional à corrente e à indutância do dispositivo. Pode-se mostrar que a energia armazenada em um indutor\( E_{ind}\) is given by

\[E_{ind} = \dfrac{1}{2}LI^2.\]

Essa expressão é semelhante à da energia armazenada em um capacitor.

Exemplo \(\PageIndex{1}\): Calculating the Energy Stored in the Field of a Solenoid

Quanta energia é armazenada no indutor de 0,632 mH do exemplo anterior quando uma corrente de 30,0 A passa por ele?

Estratégia

A energia é dada pela equação e todas as quantidades\(E_{ind} = \frac{1}{2}LI^2\), exceto elas,\(E_{ind}\) são conhecidas.

Solução

Substituindo o valor\(L\) encontrado no exemplo anterior e a corrente fornecida em\(E_{ind} = \frac{1}{2}LI^2\) dá

\[E_{ind} = \dfrac{1}{2}LI^2\]

\[0.5(0.632 \times 10^{-3} \, H)(30.0 \, A)^2 = 0.284 \, J.\]

Discussão

Essa quantidade de energia certamente é suficiente para causar uma faísca se a corrente for desligada repentinamente. Ele não pode ser construído instantaneamente, a menos que a entrada de energia seja infinita.

Resumo

A indutância é a propriedade de um dispositivo que indica a eficácia com que ele induz um emf em outro dispositivo.
A indutância mútua é o efeito de dois dispositivos na indução de emfs um no outro.
Uma mudança na corrente\(\Delta I_1/\Delta t\) em um induz e\(emf_2\) no segundo:\[emf_2 = - M\dfrac{\Delta I_1}{\Delta t},\] onde\(M\) é definida como sendo a indutância mútua entre os dois dispositivos, e o sinal de menos é devido à lei de Lenz.
Simetricamente, uma mudança na corrente\(\Delta I_2/\Delta t\) através do segundo dispositivo induz um\(emf_2\) no primeiro:\[emf_1 = -M\dfrac{\Delta I_2}{\Delta t},\] onde\(M\) está a mesma indutância mútua do processo inverso.
As mudanças atuais em um dispositivo induzem um EMF no próprio dispositivo.
A autoindutância é o efeito do dispositivo induzir emf em si mesmo.
O dispositivo é chamado de indutor, e o emf induzido nele por uma mudança na corrente através dele é\[emf = -L\dfrac{\Delta I}{\Delta t},\] onde\(L\) está a autoindutância do indutor e\(\Delta I/\Delta t\) é a taxa de mudança da corrente através dele. O sinal de menos indica que a emf se opõe à mudança na corrente, conforme exigido pela lei de Lenz.
A unidade de indutância própria e mútua é o henry (H), onde\(1 \, H = 1 \, \Omega \cdot s.\)
A autoindutância\(L\) de um indutor é proporcional à quantidade de fluxo que muda com a corrente. Para um indutor de volta N,\[L = N\dfrac{\Delta \Phi}{\Delta I}.\]
A autoindutância de um solenóide\(N\) é\[L = \dfrac{\mu_0 N^2A}{l}(solenoid),\] onde está o número de voltas no solenóide,\(A\) sua área de seção transversal,\(l\) seu comprimento e\(\mu_0 = 4\pi \times 10^{-7} \, T \cdot m/A\) é a permeabilidade do espaço livre.
A energia armazenada em um indutor\(E_{ind}\) é\[E_{ind} = \dfrac{1}{2} LI^2.\]

Glossário

indutância: uma propriedade de um dispositivo descrevendo o quão eficiente ele é em induzir emf em outro dispositivo

indutância mútua: quão eficaz um par de dispositivos é em induzir emfs um no outro

henry: a unidade de indutância;\(1 \, H = 1 \Omega \cdot s\)

autoindutância: quão eficaz um dispositivo é na indução de emf em si

indutor: um dispositivo que apresenta autoindutância significativa

energia armazenada em um indutor: autoexplicativo; calculado por\(E_{ind} = \frac{1}{2} LI^2\)

Colaboradores

Template:ContribOpenStaxCollege