23.6: Emf emocional

Last updated
Save as PDF

Page ID: 195044

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Calcule emf, força, campo magnético e trabalhe devido ao movimento de um objeto em um campo magnético.

Como vimos, qualquer alteração no fluxo magnético induz um emf oposto a essa mudança - um processo conhecido como indução. O movimento é uma das principais causas de indução. Por exemplo, um ímã movido em direção a uma bobina induz um emf, e uma bobina movida em direção a um ímã produz um emf semelhante. Nesta seção, nos concentramos no movimento em um campo magnético que é estacionário em relação à Terra, produzindo o que é vagamente chamado de emf mocional.

Uma situação em que ocorre emf mocional é conhecida como efeito Hall e já foi examinada. Cargas que se movem em um campo magnético experimentam a força magnética\(F = qvB\sin{\theta}\), que move cargas opostas em direções opostas e produz uma\(emf = Blv\). Vimos que o efeito Hall tem aplicações, incluindo medições de\(B\)\(v\) e. Agora veremos que o efeito Hall é um aspecto do fenômeno mais amplo da indução, e descobriremos que o emf mocional pode ser usado como fonte de energia.

Considere a situação mostrada na Figura\(\PageIndex{1}\). Uma haste é movida a uma velocidade\(v\) ao longo de um par de trilhos condutores separados por uma distância\(l\) em um campo magnético uniforme\(B\). Os trilhos são estacionários em relação a um resistor estacionário\(B\) e conectados a um resistor estacionário\(R\). O resistor pode ser qualquer coisa, desde uma lâmpada até um voltímetro. Considere a área delimitada pela haste móvel, trilhos e resistor. \(B\)é perpendicular a essa área e a área aumenta à medida que a haste se move. Assim, o fluxo magnético fechado pelos trilhos, haste e resistor está aumentando. Quando o fluxo muda, um emf é induzido de acordo com a lei de indução de Faraday.

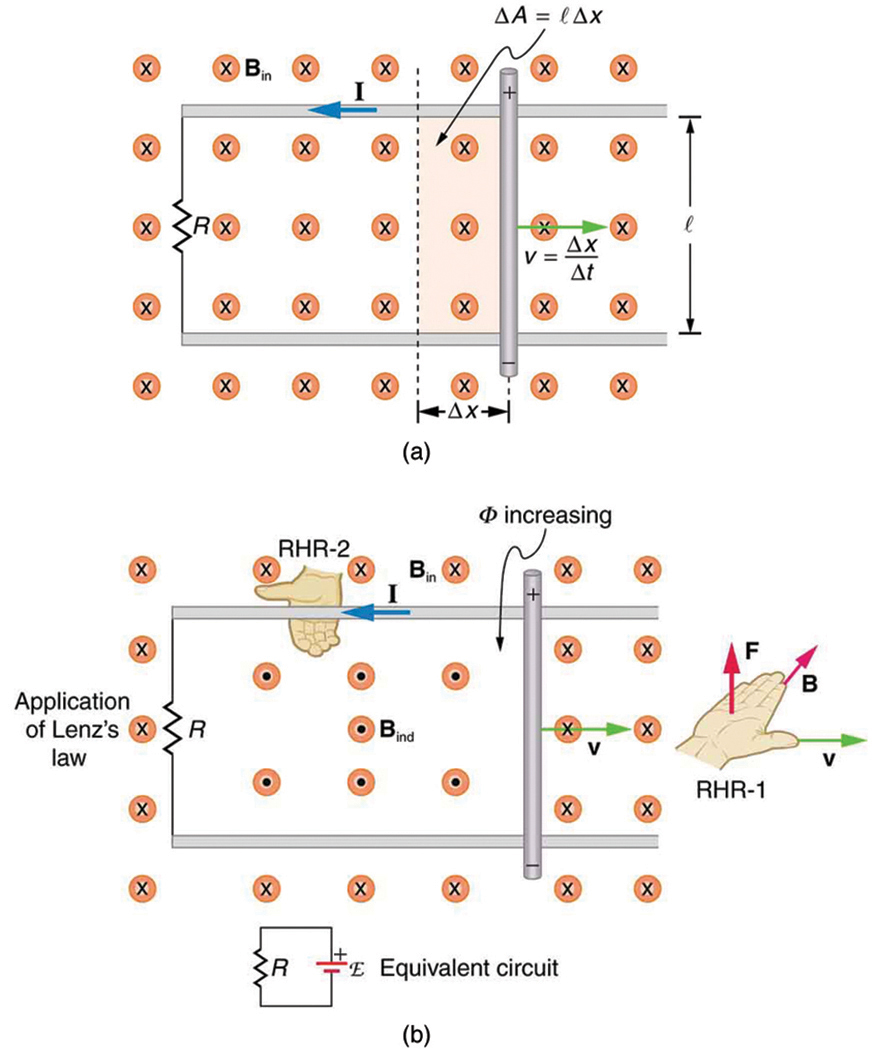
A parte a da figura mostra dois trilhos paralelos mantidos horizontalmente à distância l em um campo magnético uniforme B in, direcionado para o plano do papel. Uma resistência R está conectada em uma de suas extremidades. Uma haste é mantida vertical no meio dos trilhos e movida para a direita por uma distância delta x com uma velocidade v. a velocidade v é dada pelo delta x dividida pelo delta t. A área retangular entre a posição inicial da haste e a posição final após um movimento de delta x é dada como delta A. é igual a l multiplicado por delta x. Há uma corrente induzida, I no trilho superior para a esquerda. A extremidade superior da haste é mostrada como positiva e a extremidade inferior negativa. A parte b do diagrama mostra a mesma disposição da parte a. Dois trilhos paralelos mantidos horizontalmente à distância l em um campo magnético uniforme B in, direcionados para o plano do papel. Uma resistência está conectada em uma de suas extremidades. Uma haste é mantida vertical no meio dos trilhos e movida para a direita uma distância delta x com uma velocidade v. a lei de Lenz é aplicada e a direção do campo induzido e da corrente é mostrada. Há uma corrente induzida I no trilho superior em direção à esquerda. A extremidade superior da haste é mostrada como positiva e a extremidade inferior negativa. O campo induzido B ind é mostrado na área entre a resistência R, a haste e os trilhos. O campo induzido é oposto ao campo aplicado. O campo induzido aponta para longe do papel. O fluxo phi é mostrado aumentando na área fechada. Uma imagem da mão direita com os dedos e o polegar esticados é mostrada à direita da imagem para explicar a regra da mão direita. Um circuito equivalente da figura acima é mostrado como equivalente a uma célula de e m f conectada através de uma resistência R. — Figura\(\PageIndex{1}\): (a) Um movimento\(emf = Blv\) é induzido entre os trilhos quando essa haste se move para a direita no campo magnético uniforme. O campo magnético\(B\) está na página, perpendicular à haste móvel e aos trilhos e, portanto, à área delimitada por eles. (b) A lei de Lenz fornece as direções do campo e da corrente induzidos e a polaridade do emf induzido. Como o fluxo está aumentando, o campo induzido está na direção oposta ou fora da página. O RHR-2 fornece a direção da corrente mostrada e a polaridade da haste acionará essa corrente. O RHR-1 também indica a mesma polaridade para a haste. (Observe que o símbolo do script E usado no circuito equivalente na parte inferior da parte (b) representa emf.)

Para encontrar a magnitude do emf induzido ao longo da haste móvel, usamos a lei de indução de Faraday sem o sinal:

\[emf = N\frac{\Delta \Phi}{\Delta t}.\label{23.4.1}\]

Aqui e abaixo, “emf” implica a magnitude do emf. Nesta equação,\(N = 1\) e o fluxo\(\Phi = BA\cos{\theta}\). Nós temos\(\theta = 0^{\circ}\) e\(\cos{\theta} = 1\), uma vez que\(B\) é perpendicular\(A\) a. Agora\(\Delta \Phi = \Delta \left(BA\right) = B \Delta A\), já que\(B\) é uniforme. Observe que a área varrida pela haste é\(\Delta A = l\Delta x\). Inserindo essas quantidades na expressão para rendimentos de emf

\[emf = \frac{B\Delta A}{\Delta t} = B\frac{l\Delta x}{\Delta t}.\label{23.4.2}\]

Finalmente, observe isso\(\Delta x/ \Delta t = v\), a velocidade da haste. Inserir isso na última expressão mostra que

\[emf = Blv \left(B, l, and \quad v \quad perpendicular\right)\label{23.4.3}\]

é o emf emocional. Essa é a mesma expressão dada anteriormente para o efeito Hall..

FAZENDO CONEXÕES: UNIFICAÇÃO DE FORÇAS:

Há muitas conexões entre a força elétrica e a força magnética. O fato de um campo elétrico em movimento produzir um campo magnético e, inversamente, um campo magnético em movimento produzir um campo elétrico é parte do motivo pelo qual as forças elétricas e magnéticas agora são consideradas manifestações diferentes da mesma força. Essa unificação clássica das forças elétricas e magnéticas na chamada força eletromagnética é a inspiração para os esforços contemporâneos para unificar outras forças básicas.

Para encontrar a direção do campo induzido, a direção da corrente e a polaridade do emf induzido, aplicamos a lei de Lenz conforme explicado em “Lei da Indução de Faraday: Lei de Lenz” (Figura\(\PageIndex{1b}\)).

O fluxo está aumentando, pois a área fechada está aumentando. Assim, o campo induzido deve se opor ao existente e estar fora da página. Portanto, o RHR-2 exige que eu esteja no sentido anti-horário, o que, por sua vez, significa que a parte superior da haste está positiva, conforme mostrado.

A emf mocional também ocorre se o campo magnético se mover e a haste (ou outro objeto) estiver estacionária em relação à Terra (ou a algum observador). Vimos um exemplo disso na situação em que um ímã em movimento induz um emf em uma bobina estacionária. É o movimento relativo que é importante. O que está surgindo nessas observações é uma conexão entre campos magnéticos e elétricos. Um campo magnético em movimento produz um campo elétrico por meio de sua emf induzida. Já vimos que um campo elétrico em movimento produz um campo magnético — a carga móvel implica um campo elétrico em movimento e a carga em movimento produz um campo magnético.

Os eletromagnéticos mocionais no campo magnético fraco da Terra normalmente não são muito grandes, ou notaríamos voltagem ao longo de hastes de metal, como uma chave de fenda, durante movimentos comuns. Por exemplo, um cálculo simples da emf de movimento de uma haste de 1 m movendo-se a 3,0 m/s perpendicularmente ao campo da Terra fornece\(emf = Blv = \left(5.0 \times 10^{-5} T\right)\left(1.0 m\right)\left(3.0 m/s\right) = 150 \mu V\). Esse pequeno valor é consistente com a experiência. No entanto, há uma exceção espetacular. Em 1992 e 1996, foram feitas tentativas com o ônibus espacial para criar grandes emfs emocionais. O Satélite Tethered deveria ser solto em um fio de 20 km, conforme mostrado na Figura 2, para criar um emf de 5 kV movendo-se em velocidade orbital pelo campo da Terra. Esse emf pode ser usado para converter parte da energia cinética e potencial do ônibus espacial em energia elétrica se um circuito completo pudesse ser feito. Para completar o circuito, a ionosfera estacionária deveria fornecer um caminho de retorno para que a corrente fluísse. (A ionosfera é a atmosfera rarefeita e parcialmente ionizada em altitudes orbitais. Ele conduz por causa da ionização. A ionosfera tem a mesma função que os trilhos estacionários e o resistor de conexão na Figura 1, sem os quais não haveria um circuito completo.) Arrastar a corrente no cabo devido à força magnética\(F = IlB\sin{\theta}\) faz o trabalho que reduz a energia cinética e potencial da lançadeira e permite que ela seja convertida em energia elétrica. Ambos os testes não tiveram sucesso. No primeiro, o cabo desligou e só podia ser estendido por algumas centenas de metros; no segundo, o cabo quebrou quando estava quase totalmente estendido. O exemplo abaixo indica viabilidade em princípio.

Exemplo\(\PageIndex{1}\): Calculating the Large Motional Emf of an Object in Orbit

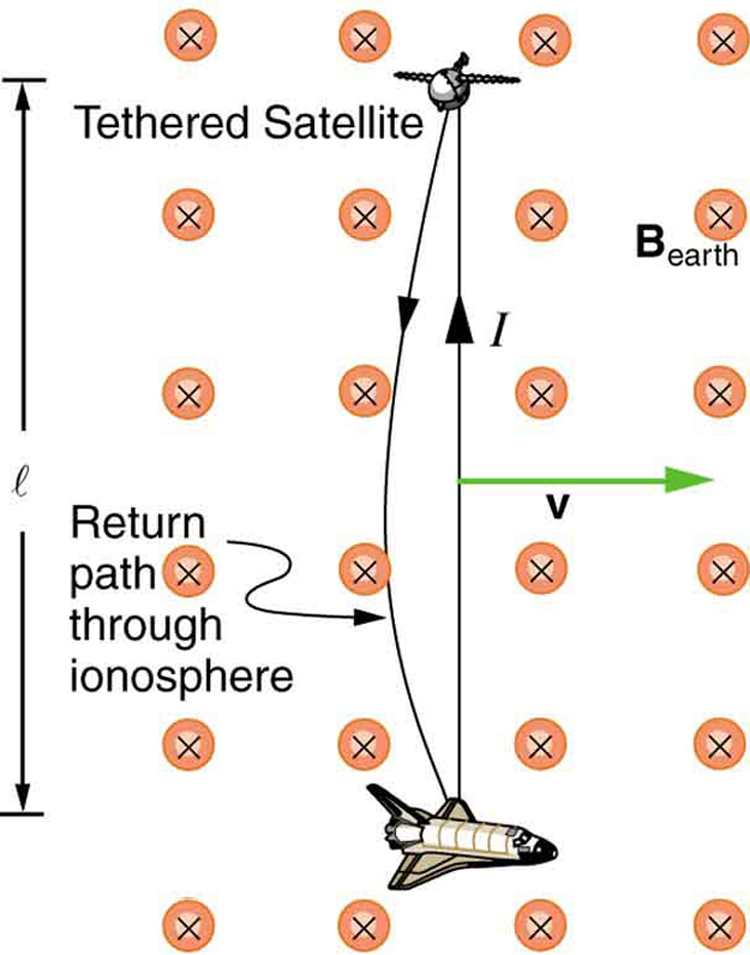
A figura mostra um satélite conectado na órbita da Terra. O campo magnético da Terra é dado como B Terra direcionada para o plano do papel. Um satélite de cabo é um satélite conectado a outro por um cabo espacial. Uma aeronave é mostrada voando à distância l abaixo do satélite conectado. Um caminho atual é mostrado da aeronave voando na ionosfera até o satélite conectado e vice-versa. — Figura\(\PageIndex{2}\): A emf mocional como conversão de energia elétrica para o ônibus espacial é a motivação para o experimento do Satélite Tethered. Previu-se que um emf de 5 kV fosse induzido na corda de 20 km de comprimento enquanto se movia em velocidade orbital no campo magnético da Terra. O circuito é completado por um caminho de retorno através da ionosfera estacionária.

Calcule a emf mocional induzida ao longo de um condutor de 20,0 km de comprimento que se move a uma velocidade orbital de 7,80 km/s perpendicular ao campo\(5.00 \times 10^{-5} T\) magnético da Terra.

Estratégia:

Esta é uma aplicação direta da expressão para emf— mocional\(emf = Blv\).

Solução:

Inserindo os valores fornecidos em\(emf = Blv\) dá\[emf = Blv\]\[= \left(5.00 \times 10^{-5} T\right)\left(2.0 \times 10^{4} m\right)\left(7.80 \times 10^{3} m/s\right)\]\[= 7.80 \times 10^{3} V.\]

Discussão:

O valor obtido é maior do que a tensão medida de 5 kV para o experimento do ônibus espacial, uma vez que o movimento orbital real da corda não é perpendicular ao campo terrestre. O valor de 7,80 kV é o emf máximo obtido quando\(\theta = 90^{\circ}\)\(\sin{\theta} = 1\) e.

Resumo

Um emf induzido pelo movimento em relação a um campo magnético\(B\) é chamado de emf mocional e é dado por\[emf = Blv \left(B,l, and \quad v \quad perpendicular\right),\] onde\(l\) está o comprimento do objeto se movendo em velocidade em\(v\) relação ao campo.