Skip to main content
Global

22.4: Força do campo magnético - Força em uma carga em movimento em um campo magnético

  1. Last updated
  2. Save as PDF
  • Page ID
    194538

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva os efeitos dos campos magnéticos na movimentação de cargas.
    • Use a regra 1 da mão direita para determinar a velocidade de uma carga, a direção do campo magnético e a direção da força magnética em uma carga em movimento.
    • Calcule a força magnética em uma carga em movimento.

    Qual é o mecanismo pelo qual um ímã exerce força sobre outro? A resposta está relacionada ao fato de que todo magnetismo é causado pela corrente, pelo fluxo de carga. Os campos magnéticos exercem forças sobre cargas móveis e, portanto, exercem forças sobre outros ímãs, todos com cargas móveis.

    Regra da mão direita 1

    A força magnética em uma carga em movimento é uma das mais fundamentais conhecidas. A força magnética é tão importante quanto a força eletrostática ou de Coulomb. No entanto, a força magnética é mais complexa, tanto no número de fatores que a afetam quanto em sua direção, do que a relativamente simples força de Coulomb. A magnitude da força magnética\(F\) on a charge \(q\) moving at a speed \(v\) in a magnetic field of strength \(B\) is given by

    \[F = qvB\sin \theta,\]

    onde\(\theta\) is the angle between the directions of \(\bf{v}\) and \(\bf{B}\). This force is often called the Lorentz force. Na verdade, é assim que definimos a intensidade do campo magnético\(B\) —em termos da força sobre uma partícula carregada que se move em um campo magnético. A unidade SI para intensidade do campo magnético\(B\) é chamada de tesla (T) em homenagem ao excêntrico, mas brilhante inventor Nikola Tesla (1856-1943). Para determinar como o tesla se relaciona com outras unidades SI, resolvemos

    \[B = \frac{F}{qv \sin\theta}\]

    Porque\(\sin \theta\) não tem unidade, o tesla é

    \[1 \,T = \frac{1\, N}{C \cdot m/s} = \dfrac{1\, N}{A \cdot m}\](observe que C/s = A).

    Outra unidade menor, chamada de gauss (G), onde\(1 G = 10^{-4} T\), às vezes é usada. Os ímãs permanentes mais fortes têm campos próximos a 2 T; eletroímãs supercondutores podem atingir 10 T ou mais. O campo magnético da Terra em sua superfície é de apenas cerca\(5 \times 10^{-5} T\) de 0,5 G.

    A direção da força magnética\(\bf{F}\) é perpendicular ao plano formado por\(\bf{v}\) e\(\bf{B}\), conforme determinado pela regra 1 da mão direita (ou RHR-1), ilustrada na Figura\(\PageIndex{1}\). O RHR-1 afirma que, para determinar a direção da força magnética em uma carga móvel positiva, você aponta o polegar da mão direita na direção de\(v\), os dedos na direção de\(\bf{B}\) e uma perpendicular à palma aponta na direção de\(\bf{F}\). Uma maneira de lembrar isso é que há uma velocidade e, portanto, o polegar a representa. Há muitas linhas de campo e, portanto, os dedos as representam. A força está na direção que você empurraria com a palma da mão. A força em uma carga negativa está exatamente na direção oposta à de uma carga positiva.

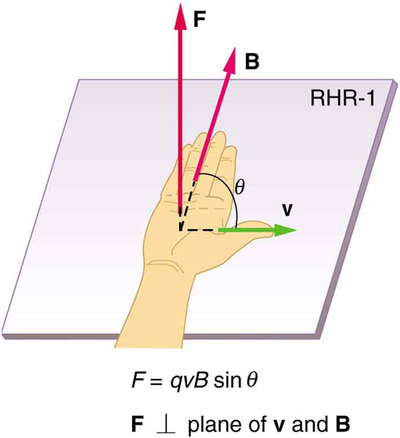
    A regra da mão direita 1. Uma mão direita estendida apoia a palma da mão sobre um pedaço de papel no qual uma seta vetorial v aponta para a direita e uma seta vetorial B aponta para a parte superior do papel. O polegar aponta para a direita, na direção da seta vetorial v. Os dedos apontam na direção do vetor B. B e v estão no mesmo plano. O vetor F aponta diretamente para cima, perpendicularmente ao plano do papel, que é o plano feito por B e v. O ângulo entre B e v é teta. A magnitude da força magnética F é igual a q v B seno teta.
    Figura\(\PageIndex{1}\): Os campos magnéticos exercem forças sobre cargas em movimento. Essa força é uma das mais básicas conhecidas. A direção da força magnética em uma carga em movimento é perpendicular ao plano formado por\(\bf{v}\)\(\bf{B}\) e segue a regra da mão direita—1 (RHR-1) conforme mostrado. A magnitude da força é proporcional a\(q\)\(v\),\(B\), e o seno do ângulo entre\(\bf{v}\)\(\bf{B}\) e.

    FAZENDO CONEXÕES: CARGAS E ÍMÃS

    Não há força magnética nas cargas estáticas. No entanto, há uma força magnética na movimentação de cargas. Quando as cargas estão estacionárias, seus campos elétricos não afetam os ímãs. Mas, quando as cargas se movem, elas produzem campos magnéticos que exercem forças sobre outros ímãs. Quando há movimento relativo, surge uma conexão entre os campos elétrico e magnético — cada um afeta o outro.

    Exemplo\(\PageIndex{1}\): Calculating Magnetic Force: Earth's Magnetic Field on a Charged Glass Rod

    Com exceção das bússolas, você raramente vê ou experimenta pessoalmente forças devido ao pequeno campo magnético da Terra. Para ilustrar isso, suponha que em um laboratório de física você esfregue uma haste de vidro com seda, colocando uma carga positiva de 20 nC nela. Calcule a força na haste devido ao campo magnético da Terra, se você lançá-la com uma velocidade horizontal de 10 m/s para oeste em um local onde o campo da Terra esteja paralelo ao norte ao solo. (A direção da força é determinada com a regra 1 da mão direita, conforme mostrado na Figura\(\PageIndex{2}\)).

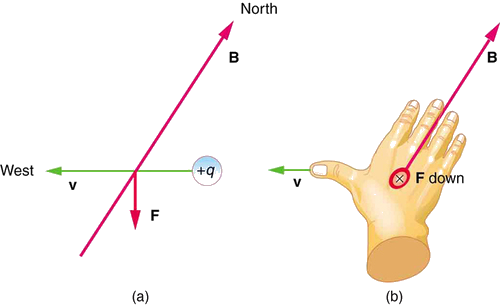
    Os efeitos do campo magnético da Terra nas cargas móveis. A Figura a mostra uma carga positiva com um vetor de velocidade a oeste, uma linha de campo magnético B orientada para o norte e um vetor de força magnética F diretamente para baixo. A Figura b mostra a mão direita voltada para baixo, com os dedos apontando para o norte com B, o polegar apontando para o oeste com v e a força para baixo para longe da mão.
    Figura\(\PageIndex{2}\): Um objeto com carga positiva que se move para o oeste em uma região onde o campo magnético da Terra está voltado para o norte experimenta uma força que é diretamente para baixo, conforme mostrado. Uma carga negativa se movendo na mesma direção sentiria uma força direta.

    Estratégia

    Recebemos a carga, sua velocidade e a força e direção do campo magnético. Assim, podemos usar a equação\(F = qvB \sin\theta\) para encontrar a força.

    Solução

    A força magnética é

    \[F = qvB \sin \theta. \nonumber\]

    Vemos isso\(sin \theta = 1\), já que o ângulo entre a velocidade e a direção do campo é\(90^{\circ}\). Inserindo as outras quantidades fornecidas, rende

    \[ \begin{align*} F &= \left(20 \times 10^{-9} C\right) \left(10 m/s \right) \left(5 \times 10^{-5} T \right) \\[5pt] &= 1 \times 10^{-11} \left(C \cdot m/s \right) \left( \frac{N}{C \cdot m/s} \right) \\[5pt] &= 1 \times 10^{-11} N . \end{align*}\]

    Discussão

    Essa força é completamente insignificante em qualquer objeto macroscópico, consistente com a experiência. (É calculado com apenas um dígito, pois o campo da Terra varia com a localização e é dado a apenas um dígito.) O campo magnético da Terra, no entanto, produz efeitos muito importantes, particularmente em partículas submicroscópicas. Alguns deles são explorados na próxima seção.

    Resumo

    • Os campos magnéticos exercem uma força sobre uma carga móvel q, cuja magnitude é\[F = qvB sin \theta , \nonumber \] onde\(\theta\) está o ângulo entre as direções de\(v\)\(B\) e.
    • A unidade SI para intensidade do campo magnético\(B\) é o tesla (T), que está relacionado a outras unidades por\[1 T = \frac{1N}{C \cdot m/s} = \frac{1 N}{A \cdot m}. \nonumber\]
    • A direção da força em uma carga em movimento é dada pela regra 1 da mão direita (RHR-1): aponte o polegar da mão direita na direção de\(v\), os dedos na direção de\(B\) e uma perpendicular à palma aponta na direção de\(F\).
    • A força é perpendicular ao plano formado por\(\mathbf{v}\)\(\mathbf{B}\) e. Como a força é zero se\(\mathbf{v}\) for paralela\(\mathbf{B}\), as partículas carregadas geralmente seguem as linhas do campo magnético em vez de cruzá-las.

    Glossário

    regra 1 da mão direita (RHR-1)
    a regra para determinar a direção da força magnética em uma carga móvel positiva: quando o polegar da mão direita aponta na direção da velocidade da carga\(v\) e os dedos apontam na direção do campo magnético \(B\), a força na carga é perpendicular e longe da palma da mão; a força em uma carga negativa é perpendicular e na palma da mão
    Força de Lorentz
    a força sobre uma carga que se move em um campo magnético
    tesla
    T, a unidade SI da intensidade do campo magnético;\(1 T=\frac{1 N}{A⋅m}\)
    força magnética
    a força sobre uma carga produzida por seu movimento através de um campo magnético; a força de Lorentz
    gauss
    G, a unidade da intensidade do campo magnético;\(1 G=10^{–4}T\) 10 —4 T