21.3: Regras de Kirchhoff

Last updated
Save as PDF

Page ID: 194063

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Analise um circuito complexo usando as regras de Kirchhoff, usando as convenções para determinar os sinais corretos de vários termos.

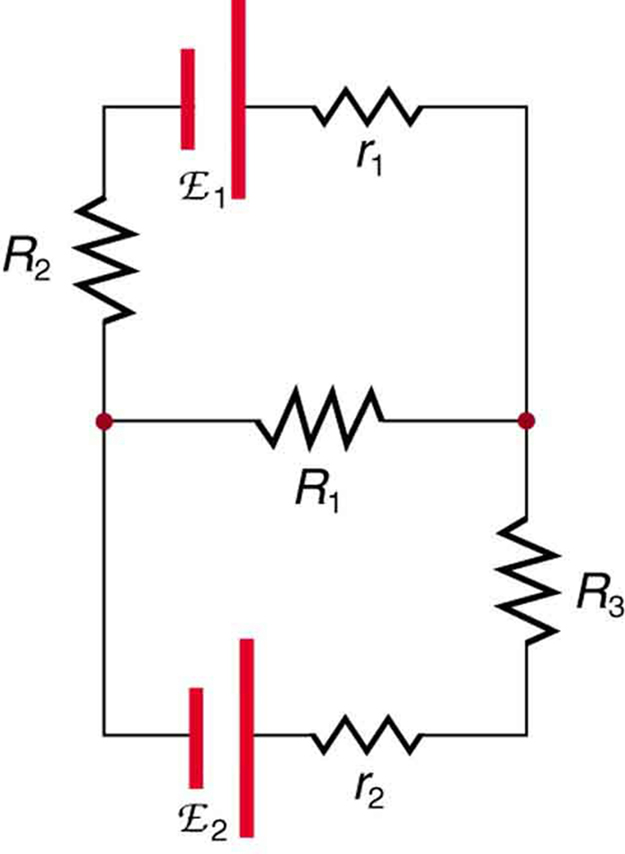
Muitos circuitos complexos, como o da Figura\(\PageIndex{1}\), não podem ser analisados com as técnicas em série paralelas desenvolvidas em Resistores em Série e Força Paralela e Eletromotriz: Tensão Terminal. Existem, no entanto, duas regras de análise de circuitos que podem ser usadas para analisar qualquer circuito, simples ou complexo. Essas regras são casos especiais das leis de conservação de carga e conservação de energia. As regras são conhecidas como regras de Kirchhoff, em homenagem ao inventor Gustav Kirchhoff (1824—1887).

Um diagrama de circuito complicado mostra várias resistências e fontes de tensão conectadas em série e em paralelo. O circuito tem três braços. O primeiro tem uma célula de e m f script E sub um e resistência interna r sub um em série com um resistor R sub dois. A segunda tem uma célula de e m f script E sub dois e resistência interna r sub dois em série com resistor R sub três. O terceiro braço tem um resistor R sub one. Os três braços estão conectados em paralelo. — Figura\(\PageIndex{1}\): Este circuito não pode ser reduzido a uma combinação de conexões em série e paralelas. As regras de Kirchhoff, aplicações especiais das leis de conservação de carga e energia, podem ser usadas para analisá-las. (Nota: O script E na figura representa a força eletromotriz, emf.)

Definição: Regras de Kirchhoff

A primeira regra de Kirchhoff — a regra de junção: A soma de todas as correntes que entram em uma junção deve ser igual à soma de todas as correntes que saem da junção.
A segunda regra de Kirchhoff — a regra do loop: A soma algébrica das mudanças no potencial em torno de qualquer caminho de circuito fechado (loop) deve ser zero.

Agora serão dadas explicações sobre as duas regras, seguidas por dicas de resolução de problemas para aplicar as regras de Kirchhoff e um exemplo prático que as usa.

Primeira regra de Kirchhoff (A regra de junção)

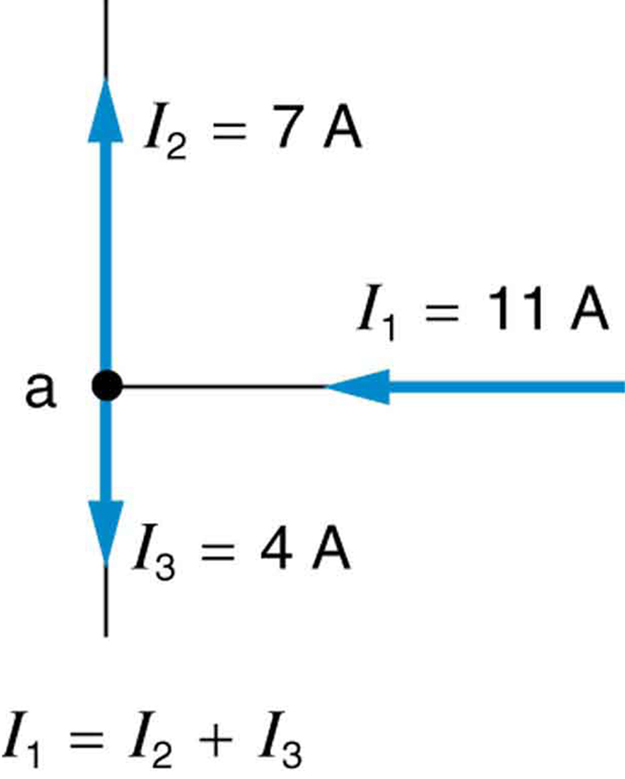
A primeira regra de Kirchhoff (a regra de junção) é uma aplicação da conservação da carga a uma junção; ela é ilustrada na Figura\(\PageIndex{2}\). A corrente é o fluxo de carga e a carga é conservada; portanto, qualquer carga que flua para a junção deve fluir para fora. A primeira regra de Kirchhoff exige isso\(I_1 = I_2 + I_3\) (Figura\(\PageIndex{2}\)). Equações como essa podem e serão usadas para analisar circuitos e resolver problemas de circuitos.

Este desenho esquemático mostra uma junção em T, com uma corrente I sub uma fluindo para o T e duas correntes I sub duas e I sub três fluindo para fora da junção T. — Figura\(\PageIndex{2}\): A regra de junção. O diagrama mostra um exemplo da primeira regra de Kirchhoff em que a soma das correntes em uma junção é igual à soma das correntes de uma junção. Nesse caso, a corrente que entra na junção se divide e sai como duas correntes, de modo que\(I_1 = I_2 + I_3\). Aqui\(I_1\) deve ser 11 A, já que\(I_2\) é 7 A e\(I_3\) é 4A.

Segunda regra de Kirchhoff (A regra de loop)

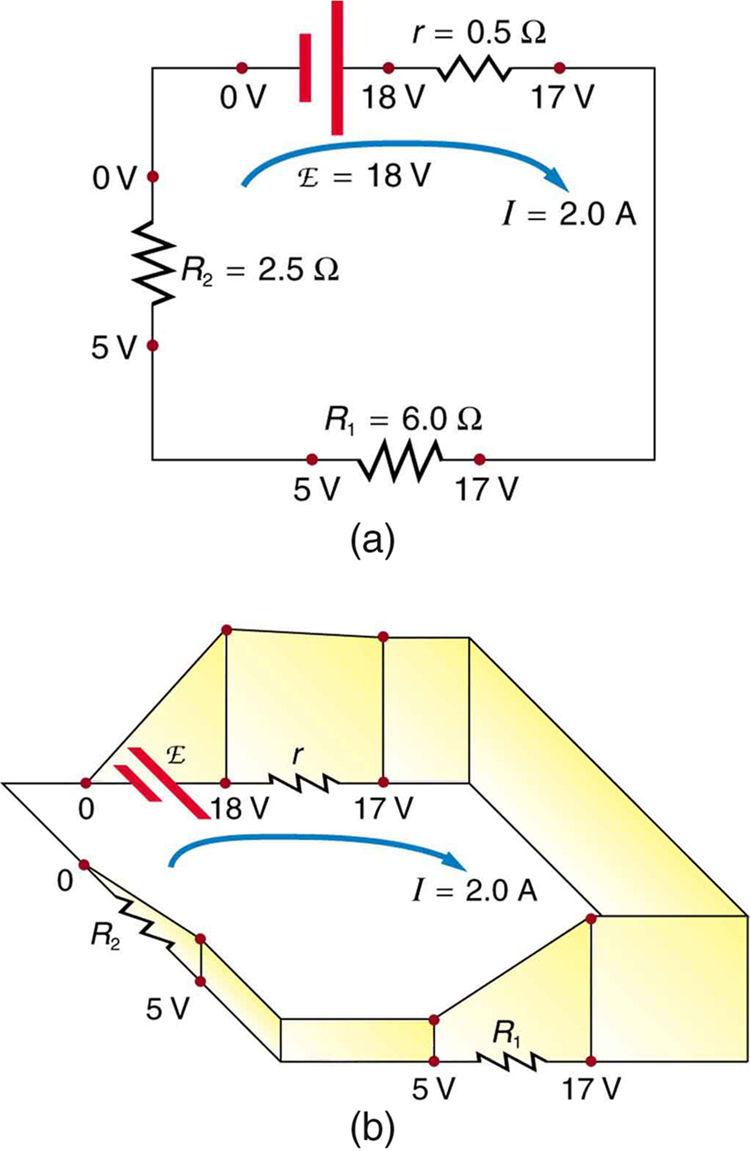
A segunda regra de Kirchhoff (a regra do loop) é uma aplicação da conservação de energia. A regra do loop é declarada em termos de potencial, em vez de energia potencial, mas as duas estão relacionadas desde então\(PE_{elec} = qV\). Lembre-se de que emf é a diferença de potencial de uma fonte quando nenhuma corrente está fluindo. Em um circuito fechado, qualquer energia fornecida pelo emf deve ser transferida para outras formas por dispositivos no circuito, pois não há outras maneiras pelas quais a energia possa ser transferida para dentro ou para fora do circuito. A figura\(\PageIndex{3}\) ilustra as mudanças de potencial em um circuito de circuito em série simples.

A segunda regra de Kirchhoff exige\(emf - Ir - IR_1 - IR_2 = 0\). Reorganizado, isto é\(emf = Ir + IR_1 + IR_2\), o que significa que o emf é igual à soma das quedas\(IR\) (de tensão) no circuito.

A parte a mostra um esquema de um circuito simples que tem uma fonte de tensão em série com dois resistores de carga. A fonte de tensão tem um e m f, rotulado script E, de dezoito volts. As quedas de tensão são de um volt na resistência interna e doze volts e cinco volts nas duas resistências de carga. A parte b é um desenho em perspectiva correspondente ao circuito na parte a. A carga é aumentada em potencial pelo e m f e diminuída pelas resistências. — Figura\(\PageIndex{3}\): A regra do loop. Um exemplo da segunda regra de Kirchhoff em que a soma das mudanças de potencial em torno de um circuito fechado deve ser zero. (a) Neste esquema padrão de um circuito em série simples, o emf fornece 18 V, que é reduzido a zero pelas resistências, com 1 V na resistência interna e 12 V e 5 V nas duas resistências de carga, totalizando 18 V. (b) Essa visão em perspectiva representa o potencial como algo como um montanha-russa, onde a carga é aumentada em potencial pelo emf e diminuída pelas resistências. (Observe que o script E significa emf.)

Aplicando as regras de Kirchhoff

Ao aplicar as regras de Kirchhoff, geramos equações que nos permitem encontrar as incógnitas nos circuitos. As incógnitas podem ser correntes, emfs ou resistências. Cada vez que uma regra é aplicada, uma equação é produzida. Se houver tantas equações independentes quanto incógnitas, o problema poderá ser resolvido. Há duas decisões que você deve tomar ao aplicar as regras de Kirchhoff. Essas decisões determinam os sinais de várias quantidades nas equações que você obtém ao aplicar as regras.

Ao aplicar a primeira regra de Kirchhoff, a regra de junção, você deve rotular a corrente em cada ramificação e decidir em que direção ela está indo. Por exemplo, em Figura, Figura e Figura, as correntes são rotuladas\(I_1, \, I_2, \, I_3\) e\(I\) as setas indicam suas direções. Não há risco aqui, pois se você escolher a direção errada, a corrente será da magnitude correta, mas negativa.
Ao aplicar a segunda regra de Kirchhoff, a regra do loop, você deve identificar um circuito fechado e decidir em qual direção contorná-lo, no sentido horário ou anti-horário. Por exemplo, na Figura, o circuito foi percorrido na mesma direção da corrente (no sentido horário). Novamente, não há risco; contornar o circuito na direção oposta inverte o sinal de cada termo na equação, o que é como multiplicar os dois lados da equação por -1.

A figura\(\PageIndex{4}\) e os pontos a seguir ajudarão você a acertar os sinais de mais ou menos ao aplicar a regra de loop. Observe que os resistores e os emfs são percorridos indo de a a b. Em muitos circuitos, será necessário construir mais de um loop. Ao percorrer cada ciclo, é preciso ser consistente quanto ao sinal da mudança de potencial (exemplo\(\PageIndex{1}\)).

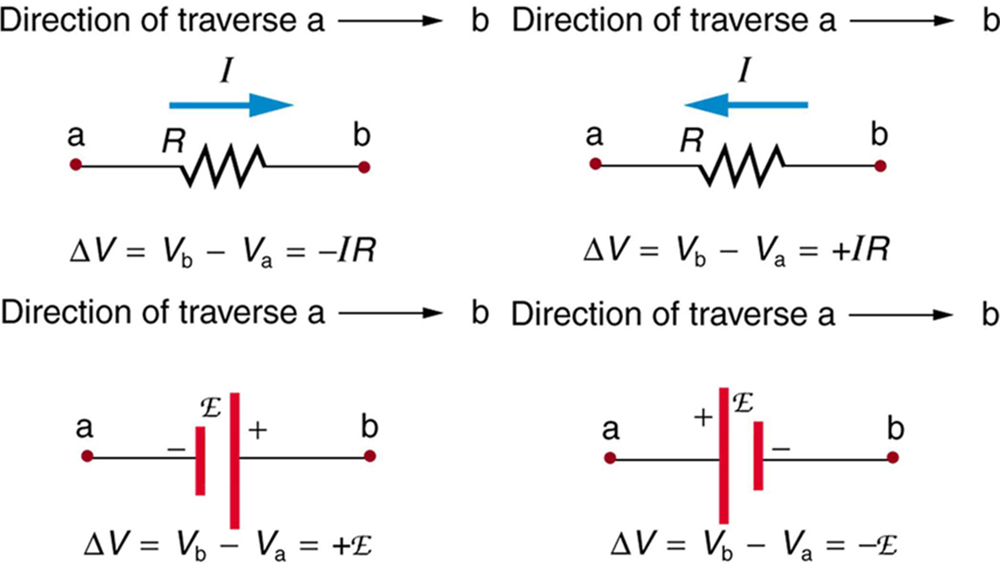
Esta figura mostra quatro situações em que a corrente flui através de um resistor ou de uma fonte e o cálculo da mudança potencial em cada uma. Os dois primeiros diagramas mostram a queda de potencial em um resistor, com a corrente fluindo da esquerda para a direita ou da direita para a esquerda. Os outros dois diagramas mostram uma queda potencial em uma fonte de tensão, quando os terminais estão em uma orientação e depois em outra. — Figura\(\PageIndex{4}\): Cada um desses resistores e fontes de tensão é atravessado de a a b. As possíveis mudanças são mostradas abaixo de cada elemento e são explicadas no texto. (Observe que o script E significa emf.)

Quando um resistor é percorrido na mesma direção da corrente, a mudança no potencial é\(-IR\). (Veja a Figura.)
Quando um resistor é percorrido na direção oposta à corrente, a mudança no potencial é\(+IR\). (Veja a Figura.)
Quando um emf é percorrido de - para + (na mesma direção em que ele move a carga positiva), a mudança no potencial é +emf. (Veja a Figura.)
Quando um emf é percorrido de + para - (oposta à direção em que ele move a carga positiva), a mudança no potencial é -emf. (Veja a Figura.)

Exemplo\(\PageIndex{1}\): Calculating Current: Using Kirchhoff’s Rules

Encontre as correntes que fluem no circuito na Figura\(\PageIndex{5}\).

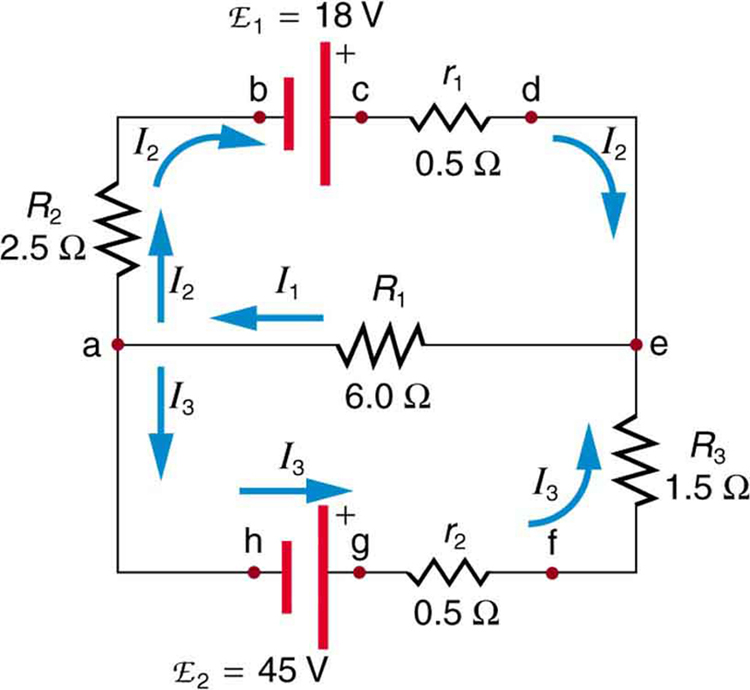
O diagrama mostra um circuito complexo com duas fontes de tensão E sub uma e E sub duas e várias cargas resistivas, conectadas em dois loops e duas junções. Vários pontos no diagrama são marcados com as letras de a a h. A corrente em cada ramificação é rotulada separadamente. — Figura, mas as resistências e os emfs são especificados. (Cada emf é indicado pelo script E.) As correntes em cada ramificação são rotuladas e presume-se que se movam nas direções mostradas. Este exemplo usa as regras de Kirchhoff para encontrar as correntes.

Estratégia

Esse circuito é suficientemente complexo para que as correntes não possam ser encontradas usando a lei de Ohm e as técnicas de séries paralelas — é necessário usar as regras de Kirchhoff. As correntes foram rotuladas\(I_1, \, I_2,\) e\(I_3\)

na figura e suposições foram feitas sobre suas direções. As localizações no diagrama foram rotuladas com as letras de a a h. Na solução, aplicaremos as regras de junção e loop, buscando três equações independentes para nos permitir resolver as três correntes desconhecidas.

Solução

Começamos aplicando a primeira regra de Kirchhoff ou a regra de junção no ponto a. Isso dá

\[I_1 = I_2 + I_3,\]

uma vez que\(I_1\) flui para a junção, enquanto\(I\) e\(I_3\) flui para fora. A aplicação da regra de junção em e produz exatamente a mesma equação, de modo que nenhuma nova informação é obtida. Essa é uma equação única com três incógnitas — três equações independentes são necessárias e, portanto, a regra do loop deve ser aplicada.

Agora, consideramos o loop abcdea. Indo de a para b, atravessamos\(R_2\) na mesma direção (assumida) da corrente\(I_2\), e assim ocorre a mudança no potencial\(-I_2R_2\). Então, indo de b para c, vamos de - para +, de modo que a mudança no potencial é\(+emf_1\). Atravessar a resistência interna\(r_1\) de c a d dá\(-I_2r_1\). Completar o loop passando de d para a novamente atravessa um resistor na mesma direção de sua corrente, dando uma mudança no potencial de\(-I_1R_1\).

A regra do loop afirma que as mudanças no potencial somam zero. Assim,

\[-I_2R_2 + emf_1 -I_2r_1 - I_1R_1 = -I_2(R_2 + r_1) + emf_1 - I_1R_1 = 0.\]

Observe que os sinais estão invertidos em comparação com o outro loop, porque os elementos são atravessados na direção oposta. Com os valores inseridos, isso se torna\[+6I_1 + 2I_3 -45 = 0.\] Essas três equações são suficientes para resolver as três correntes desconhecidas. Primeiro, resolva a segunda equação para\(I_2\).

\[I_2 = 6 - 2I_1.\]

Agora resolva a terceira equação para\(I_3\):

\[I_3 = 22.5 - 3I_1.\]

Substituir essas duas novas equações pela primeira nos permite encontrar um valor para

\[I_1 = I_2 + I_3 = (6 - 2I_1) + (22.5 - 3I_1) = 28.5 - 5I_1.\]

A combinação de termos dá

\[6I_1 = 28.5, \, and\]\[I_1 = 4.75 \, A.\]

Substituindo esse valor de\(I\) volta na quarta equação, obtém-se

\[I_2 = 6 - 2I_1 = 6 - 9.50\]\[I_2 = -3.50 \, A\]

O sinal de menos significa que\(I_2\) flui na direção oposta à assumida na Figura.

Finalmente, substituir o valor por\(I_1\) na quinta equação dá

\[I_3 = 22.5 - 3I_1 = 22.5 - 14.25\]\[I_3 = 8.25 \, A.\]

Discussão

Apenas como um cheque, notamos isso, de fato\(I_1 = I_2 + I_3\). Os resultados também poderiam ter sido verificados inserindo todos os valores na equação do loop abcdefgha.

Estratégias de resolução de problemas para as regras de Kirchhoff

Certifique-se de que haja um diagrama de circuito claro no qual você possa rotular todas as resistências, emfs e correntes conhecidas e desconhecidas. Se uma corrente for desconhecida, você deve atribuir-lhe uma direção. Isso é necessário para determinar os sinais de possíveis mudanças. Se você atribuir a direção incorretamente, descobrirá que a corrente tem um valor negativo, sem causar danos.
Aplique a regra de junção em qualquer junção no circuito. Cada vez que a regra de junção é aplicada, você deve obter uma equação com uma corrente que não aparece em uma aplicação anterior; caso contrário, a equação é redundante.
Aplique a regra de loop em quantos loops forem necessários para resolver as incógnitas do problema. (Deve haver tantas equações independentes quanto incógnitas.) Para aplicar a regra do loop, você deve escolher uma direção para contornar o loop. Em seguida, determine com cuidado e consistência os sinais das possíveis mudanças para cada elemento usando os quatro pontos com marcadores discutidos acima em conjunto com a Figura.
Resolva as equações simultâneas para as incógnitas. Isso pode envolver muitas etapas algébricas, exigindo uma verificação cuidadosa e uma nova verificação.
Verifique se as respostas são razoáveis e consistentes. Os números devem ser da ordem correta de magnitude, nem muito grandes nem extremamente pequenos. Os sinais devem ser razoáveis — por exemplo, nenhuma resistência deve ser negativa. Verifique se os valores obtidos satisfazem as várias equações obtidas com a aplicação das regras. As correntes devem satisfazer a regra de junção, por exemplo.

O material desta seção está correto em teoria. Devemos ser capazes de verificá-lo fazendo medições de corrente e tensão. Na verdade, alguns dos dispositivos usados para fazer essas medições são aplicações diretas dos princípios abordados até agora e serão explorados nos próximos módulos. Como veremos, um fato muito básico, e até mesmo profundo, resulta: fazer uma medição altera a quantidade que está sendo medida.

Exercício\(\PageIndex{1}\)

As regras de Kirchhoff podem ser aplicadas a séries simples e circuitos paralelos ou estão restritas para uso em circuitos mais complicados que não são combinações de séries e paralelos?

Responda: As regras de Kirchhoff podem ser aplicadas a qualquer circuito, pois são aplicações a circuitos de duas leis de conservação. As leis de conservação são os princípios mais amplamente aplicáveis em física. Geralmente, é matematicamente mais simples usar as regras para séries e paralelas em circuitos mais simples, então enfatizamos as regras de Kirchhoff para uso em situações mais complicadas. Mas as regras para séries e paralelos podem ser derivadas das regras de Kirchhoff. Além disso, as regras de Kirchhoff podem ser expandidas para dispositivos que não sejam resistores e emfs, como capacitores, e são um dos dispositivos básicos de análise na análise de circuitos.

Resumo

As regras de Kirchhoff podem ser usadas para analisar qualquer circuito, simples ou complexo.
A primeira regra de Kirchhoff — a regra de junção: A soma de todas as correntes que entram em uma junção deve ser igual à soma de todas as correntes que saem da junção.
A segunda regra de Kirchhoff — a regra do loop: A soma algébrica das mudanças no potencial em torno de qualquer caminho de circuito fechado (loop) deve ser zero.
As duas regras são baseadas, respectivamente, nas leis de conservação de carga e energia.
Ao calcular o potencial e a corrente usando as regras de Kirchhoff, um conjunto de convenções deve ser seguido para determinar os sinais corretos de vários termos.
As séries mais simples e as regras paralelas são casos especiais das regras de Kirchhoff.

Glossário

Regras de Kirchhoff: um conjunto de duas regras, baseadas na conservação de carga e energia, que regem a corrente e as mudanças de potencial em um circuito elétrico

regra de junção: A primeira regra de Kirchhoff, que aplica a conservação da carga a uma junção; a corrente é o fluxo de carga; portanto, qualquer carga que flua para a junção deve fluir para fora; a regra pode ser declarada\(I_1 = I+2 + I_3\)

regra de loop: A segunda regra de Kirchhoff, que afirma que em um circuito fechado, qualquer energia fornecida pelo emf deve ser transferida para outras formas por dispositivos no circuito, uma vez que não há outras maneiras pelas quais a energia possa ser transferida para dentro ou para fora do circuito. Assim, o emf é igual à soma das quedas\(IR\) (de tensão) no circuito e pode ser declarado:\(emf = Ir + IR_1 + IR_2\)

leis de conservação: exigem que a energia e a carga sejam conservadas em um sistema