20.E: Métodos de transferência de calor e calor (exercício)
- Page ID
- 194420
Perguntas conceituais
20.1: Atual
1. Um fio pode transportar uma corrente e ainda ser neutro, ou seja, ter uma carga total de zero? Explique.
2. As baterias de automóveis são avaliadas em amperes-hora (A⋅h). A que quantidade física correspondem os amperes-hora (tensão, carga,...) e que relação os amperes-hora têm com o conteúdo de energia?
3. Se dois fios diferentes com áreas de seção transversal idênticas carregarem a mesma corrente, a velocidade de desvio será maior ou menor no melhor condutor? Explique em termos da equação\(\displaystyle v_d=\frac{I}{nqA}\), considerando como a densidade dos portadores de carga se\(\displaystyle n\) relaciona com o fato de um material ser ou não um bom condutor.
4. Por que dois caminhos condutores de uma fonte de tensão para um dispositivo elétrico são necessários para operar o dispositivo?
5. Nos carros, um terminal de bateria é conectado ao corpo metálico. Como isso permite que um único fio forneça corrente para dispositivos elétricos em vez de dois fios?
6. Por que um pássaro sentado em uma linha de alta tensão não é eletrocutado? Compare isso com a situação em que um pássaro grande atinge dois fios simultaneamente com suas asas.
20.2: Lei de Ohm: Resistência e circuitos simples
7. A\(\displaystyle IR\) queda em um resistor significa que há uma mudança no potencial ou na tensão no resistor. Há alguma mudança na corrente ao passar por um resistor? Explique.
8. Como a\(\displaystyle IR\) queda em um resistor é semelhante à queda de pressão em um fluido que flui através de um tubo?
20.3: Resistência e resistividade
9. Em qual dos três materiais semicondutores listados na Tabela as impurezas fornecem taxas gratuitas? (Dica: examine a faixa de resistividade de cada um e determine se o semicondutor puro tem a maior ou menor condutividade.)
10. A resistência de um objeto depende do caminho que a corrente percorre por ele? Considere, por exemplo, uma barra retangular — sua resistência é a mesma em seu comprimento e em sua largura? (Veja a Figura.)
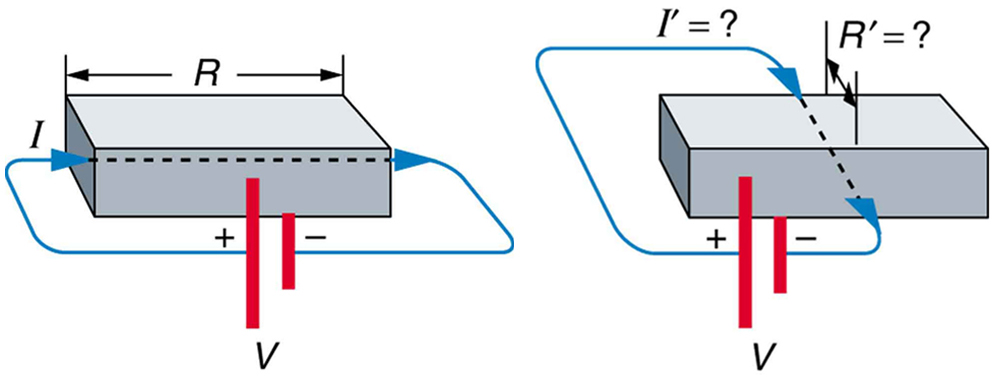
A corrente que segue dois caminhos diferentes através do mesmo objeto encontra resistência diferente?
11. Se fios de alumínio e cobre do mesmo comprimento tiverem a mesma resistência, qual tem o diâmetro maior? Por quê?
12. Explique\(\displaystyle R=R_0(1+αΔT)\) por que a variação de temperatura da resistência\(\displaystyle R\) de um objeto não é tão precisa quanto\(\displaystyle ρ=ρ_0(1+αΔT)\), o que dá a variação de temperatura da resistividade ρ tamanho 12 {ρ} {}.
20.4: Energia elétrica e energia
13. Por que as lâmpadas incandescentes escurecem tarde em suas vidas, especialmente pouco antes de seus filamentos se quebrarem?
14. A potência dissipada em um resistor é dada por\(\displaystyle P=V^2/R\), o que significa que a potência diminui se a resistência aumentar. No entanto, esse poder também é dado por\(\displaystyle P=I^2R\), o que significa que o poder aumenta se a resistência aumentar. Explique por que não há contradição aqui.
20.5: Corrente alternada versus corrente contínua
15. Dê um exemplo de uso de energia AC que não seja em casa. Da mesma forma, dê um exemplo de uso de energia DC diferente daquela fornecida por baterias.
16. Por que a tensão, a corrente e a potência passam por zero 120 vezes por segundo para eletricidade CA de 60 Hz?
17. Você está andando em um trem, olhando para a distância pela janela. À medida que objetos próximos passam, você percebe que as luzes fluorescentes próximas produzem listras tracejadas. Explique.
20.6: Riscos elétricos e o corpo humano
18. Usando um ohmímetro, o aluno mede a resistência entre vários pontos do corpo. Ele descobre que a resistência entre dois pontos no mesmo dedo é aproximadamente a mesma que a resistência entre dois pontos em mãos opostas — ambos têm várias centenas de milhares de ohms. Além disso, a resistência diminui quando mais pele entra em contato com as sondas do ohmímetro. Finalmente, há uma queda drástica na resistência (até alguns milhares de ohms) quando a pele está molhada. Explique essas observações e suas implicações em relação à pele e à resistência interna do corpo humano.
19. Quais são os dois principais riscos da eletricidade?
20. Por que um curto-circuito não é um risco de choque?
21. O que determina a gravidade de um choque? Você pode dizer que uma determinada voltagem é perigosa sem mais informações?
22. Uma agulha eletrificada é usada para queimar verrugas, com o circuito sendo concluído com o paciente sentado em uma placa de nádega grande. Por que esse prato é grande?
23. Algumas cirurgias são realizadas com eletricidade de alta voltagem passando de um bisturi de metal pelo tecido que está sendo cortado. Considerando a natureza dos campos elétricos na superfície dos condutores, por que você esperaria que a maior parte da corrente fluísse da borda afiada do bisturi? Você acha que a corrente alternada de alta ou baixa frequência é usada?
24. Alguns dispositivos frequentemente usados em banheiros, como secadores de cabelo, costumam ter mensagens de segurança dizendo “Não use quando a banheira ou a pia estiverem cheias de água”. Por que isso é assim?
25. Muitas vezes, somos aconselhados a não apertar os interruptores elétricos com as mãos molhadas, seque a mão primeiro. Também é aconselhável nunca jogar água em uma fogueira elétrica. Por que isso é assim?
26. Antes de trabalhar em uma linha de transmissão de energia, os atacantes tocarão a linha com o dorso da mão como uma verificação final de que a tensão é zero. Por que a palma da mão?
27. Por que a resistência da pele úmida é muito menor do que a seca e por que o sangue e outros fluidos corporais têm baixas resistências?
28. Uma pessoa em infusão intravenosa (IV) pode ser sensível ao microchoque?
29. Tendo em vista as pequenas correntes que causam riscos de choque e as correntes maiores que os disjuntores e fusíveis interrompem, como elas desempenham um papel na prevenção de riscos de choque?
20.7: Condução nervosa — Eletrocardiogramas
30. Observe que na Figura, tanto o gradiente de concentração quanto a força de Coulomb tendem a mover\(\displaystyle Na^+\) íons para dentro da célula. O que impede isso?
31. Defina a despolarização, a repolarização e o potencial de ação.
32. Explique as propriedades dos nervos mielinizados em termos das propriedades isolantes da mielina.
Problemas e exercícios
20.1: Atual
33. Qual é a corrente em miliamperes produzida pelas células solares de uma calculadora de bolso pela qual passam 4,00 C de carga em 4,00 h?
Solução
0,278 mA
34. Um total de 600 C de carga passa por uma lanterna em 0,500 h. Qual é a corrente média?
35. Qual é a corrente quando uma carga estática típica\(\displaystyle 0.250μC\) se move do dedo para uma maçaneta de metal\(\displaystyle 1.00μs\)?
Solução
0,250 A
36. Encontre a corrente quando 2,00 nC saltar entre o pente e o cabelo em um intervalo de\(\displaystyle 0.500 -μs\) tempo.
37. Um grande raio tinha uma corrente de 20.000 A e movia 30,0 C de carga. Qual foi sua duração?
Solução
1,50 ms
38. A corrente 200-A através de uma vela de ignição move 0,300 mC de carga. Quanto tempo dura a faísca?
39. (a) Um desfibrilador envia uma corrente de 6,00-A pelo tórax de um paciente aplicando um potencial de 10.000 V, como na figura abaixo. Qual é a resistência do caminho? (b) As pás do desfibrilador entram em contato com o paciente por meio de um gel condutor que reduz consideravelmente a resistência do caminho. Discuta as dificuldades que surgiriam se uma voltagem maior fosse usada para produzir a mesma corrente através do paciente, mas com o caminho tendo talvez 50 vezes a resistência. (Dica: a corrente deve ser quase a mesma, então uma voltagem mais alta implicaria maior potência. Use esta equação para potência:\(\displaystyle P=I^2R\).)
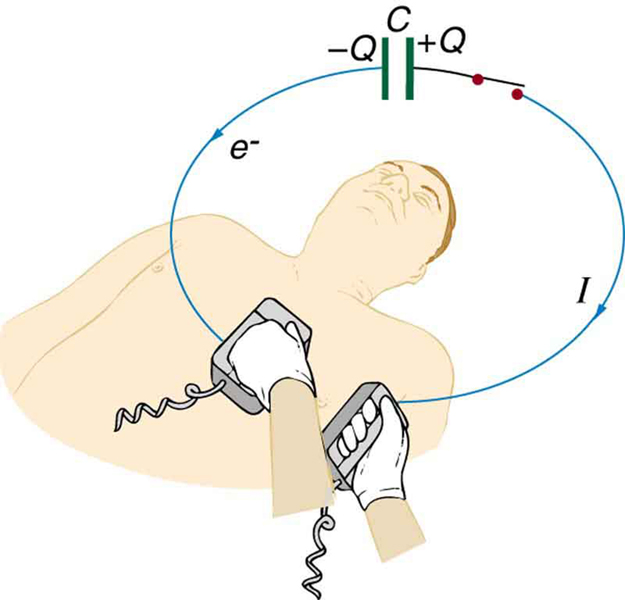
O capacitor em uma unidade de desfibrilação aciona uma corrente através do coração de um paciente.
Solução
(a)\(\displaystyle 1.67kΩ\)
(b) Se existisse uma resistência 50 vezes maior, mantendo a corrente quase a mesma, a potência seria aumentada em um fator de cerca de 50 (com base na equação\(\displaystyle P=I^2R\)), fazendo com que muito mais energia fosse transferida para a pele, o que poderia causar queimaduras graves. O gel usado reduz a resistência e, portanto, reduz a potência transferida para a pele.
40. Durante uma cirurgia cardíaca aberta, um desfibrilador pode ser usado para tirar um paciente de uma parada cardíaca. A resistência do caminho é\(\displaystyle 500 Ω\) e é necessária uma corrente de 10,0 mA. Qual voltagem deve ser aplicada?
41. (a) Um desfibrilador passa 12,0 A de corrente pelo torso de uma pessoa por 0,0100 s. Quanta carga se move?
(b) Quantos elétrons passam pelos fios conectados ao paciente? (Veja a figura dois problemas anteriores.)
Solução
(a) 0,120 C
(b)\(\displaystyle 7.50×10^{17}electrons\)
42. A bateria de um relógio se desgasta após mover 10.000 C de carga pelo relógio a uma taxa de 0,500 mA.
(a) Quanto tempo o relógio funcionou?
(b) Quantos elétrons por segundo fluíram?
43. As baterias de um submarino não nuclear submerso fornecem 1000 A a toda velocidade. Quanto tempo leva para mover o número (\(\displaystyle 6.02×10^{23}\)) de elétrons de Avogadro nesse ritmo?
Solução
96.3 s
44. Armas de elétrons são usadas em tubos de raios-X. Os elétrons são acelerados por meio de uma voltagem relativamente grande e direcionados para um alvo de metal, produzindo raios-X.
(a) Quantos elétrons por segundo atingem o alvo se a corrente for de 0,500 mA?
(b) Qual carga atinge o alvo em 0,750 s?
45. Um grande ciclotron direciona um feixe de\(\displaystyle He^{++}\) núcleos para um alvo com uma corrente de feixe de 0,250 mA.
(a) Quantos\(\displaystyle He^{++}\) núcleos por segundo são esses?
(b) Quanto tempo leva para 1,00 C atingir o alvo?
(c) Quanto tempo falta até que 1,00 mol de\(\displaystyle He^{++}\) núcleos atinjam o alvo?
Solução
(a)\(\displaystyle 7.81 × 10^{14}He^{++}nuclei/s\)
(b)\(\displaystyle 4.00 × 10^3s\)
(c)\(\displaystyle 7.71 × 10^8s\)
46. Repita o exemplo acima no Exemplo, mas para um fio feito de prata e dado, há um elétron livre por átomo de prata.
47. Usando os resultados do exemplo acima em Exemplo, determine a velocidade de desvio em um fio de cobre com o dobro do diâmetro e transportando 20,0 A.
Solução
\(\displaystyle −1.13×10^{−4}m/s\)
48. Um fio de cobre de calibre 14 tem um diâmetro de 1.628 mm. Qual magnitude a corrente flui quando a velocidade de deriva é de 1,00 mm/s? (Veja o exemplo acima em Exemplo para obter informações úteis.)
49. O SPEAR, um anel de armazenamento com cerca de 72,0 m de diâmetro no Stanford Linear Accelerator (fechado em 2009), tem um feixe circulante de elétrons de 20,0 A que se move quase à velocidade da luz. (Veja a Figura.) Quantos elétrons estão no feixe?
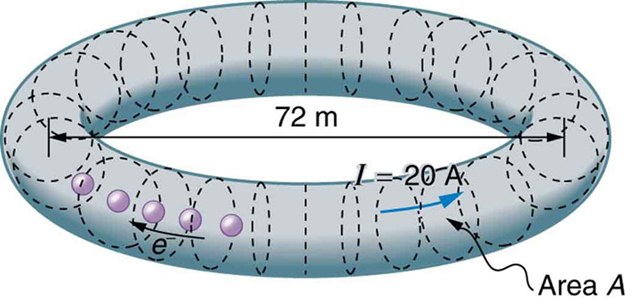
Os elétrons que circulam no anel de armazenamento chamado SPEAR constituem uma corrente de 20,0 A. Como eles viajam perto da velocidade da luz, cada elétron completa muitas órbitas em cada segundo.
Solução
\(\displaystyle 9.42×10^{13}electrons\)
20.2: Lei de Ohm: Resistência e circuitos simples
50. Qual corrente flui através da lâmpada de uma lanterna de 3,00 V quando sua resistência ao calor é\(\displaystyle 3.60 Ω\)?
Solução
0,833 A
51. Calcule a resistência efetiva de uma calculadora de bolso que tem uma bateria de 1,35 V e através da qual flui 0,200 mA.
52. Qual é a resistência efetiva do motor de partida de um carro quando 150 A passa por ele quando a bateria do carro aplica 11,0 V ao motor?
Solução
\(\displaystyle 7.33×10^{−2}Ω\)
53. Quantos volts são fornecidos para operar uma luz indicadora em um DVD player com uma resistência de\(\displaystyle 140Ω\), já que 25,0 mA passam por ele?
54. (a) Encontre a queda de tensão em um cabo de extensão com\(\displaystyle 0.0600-Ω\) resistência e através do qual 5,00 A está fluindo.
(b) Um cabo mais barato utiliza um fio mais fino e tem uma resistência de\(\displaystyle 0.300Ω\). Qual é a queda de tensão quando 5,00 A flui?
(c) Por que a voltagem de qualquer aparelho que está sendo usado é reduzida nessa quantidade? Qual é o efeito no aparelho?
Solução
(a) 0,300 V
(b) 1,50 V
(c) A tensão fornecida a qualquer aparelho que esteja sendo usado é reduzida porque a queda total de tensão da parede para a saída final do aparelho é fixa. Assim, se a queda de tensão no cabo de extensão for grande, a queda de tensão no aparelho diminuirá significativamente, portanto, a saída de energia do aparelho pode ser significativamente reduzida, reduzindo a capacidade do aparelho de funcionar corretamente.
55. Uma linha de transmissão de energia é pendurada em torres de metal com isoladores de vidro com uma resistência de\(\displaystyle 1.00×10^9Ω\). Qual corrente flui pelo isolador se a tensão for de 200 kV? (Algumas linhas de alta tensão são DC.)
20.3: Resistência e resistividade
56. Qual é a resistência de um pedaço de fio de cobre calibre 12 de 20,0 m de comprimento com um diâmetro de 2,053 mm?
Solução
0,104 Ω
57. O diâmetro do fio de cobre de calibre 0 é 8,252 mm. Encontre a resistência de um comprimento de 1,00 km desse fio usado para transmissão de energia.
58. Se o filamento de tungstênio de 0,100 mm de diâmetro em uma lâmpada tiver uma resistência de\(\displaystyle 0.200 Ω\) at\(\displaystyle 20.0ºC\), quanto tempo deve durar?
Solução
\(\displaystyle 2.8×10^{−2}m\)
59. Encontre a proporção entre o diâmetro do alumínio e do fio de cobre, se eles tiverem a mesma resistência por unidade de comprimento (como na fiação doméstica).
60. Qual corrente flui através de uma haste de silício puro de 2,54 cm de diâmetro que tem 20,0 cm de comprimento, quando\(\displaystyle 1.00 × 10^3V\) é aplicada a ela? (Essa haste pode ser usada para fazer detectores de partículas nucleares, por exemplo.)
Solução
\(\displaystyle 1.10×10^{−3}A\)
61. (a) A que temperatura você deve elevar um fio de cobre, originalmente em\(\displaystyle 20.0ºC\), para dobrar sua resistência, negligenciando quaisquer mudanças nas dimensões?
(b) Isso acontece na fiação doméstica em circunstâncias normais?
62. Um resistor feito de fio de nicromo é usado em uma aplicação em que sua resistência não pode mudar mais do que 1,00% de seu valor em\(\displaystyle 20.0ºC\). Em qual faixa de temperatura ele pode ser usado?
Solução
\(\displaystyle −5ºC\) para\(\displaystyle 45ºC\)
63. De que material um resistor é feito se sua resistência for 40,0% maior em\(\displaystyle 100ºC\) do que em\(\displaystyle 20.0ºC\)?
64. Um dispositivo eletrônico projetado para operar em qualquer temperatura na faixa de\(\displaystyle –10.0ºC\) até\(\displaystyle 55.0ºC\) contém resistores de carbono puro. Por qual fator sua resistência aumenta nessa faixa?
Solução
1.03
65. (a) De que material é feito um fio, se ele tem 25,0 m de comprimento e 0,100 mm de diâmetro e tem uma resistência de\(\displaystyle 77.7Ω\) at\(\displaystyle 20.0ºC\)?
(b) Em que consiste sua resistência\(\displaystyle 150ºC\)?
66. Supondo um coeficiente de resistividade de temperatura constante, qual é a redução percentual máxima na resistência de um fio constante a partir de\(\displaystyle 20.0ºC\)?
Solução
0,06%
67. Um fio é puxado por uma matriz, esticando-o até quatro vezes seu comprimento original. Por qual fator sua resistência aumenta?
68. Um fio de cobre tem uma resistência de\(\displaystyle 0.500Ω\) at\(\displaystyle 20.0ºC\) e um fio de ferro tem uma resistência de\(\displaystyle 0.525Ω\) na mesma temperatura. Em que temperatura suas resistências são iguais?
Solução
\(\displaystyle −17ºC\)
69. (a) Os termômetros médicos digitais determinam a temperatura medindo a resistência de um dispositivo semicondutor chamado termistor (que tem\(\displaystyle α=–0.0600/ºC\)) quando está na mesma temperatura do paciente. Qual é a temperatura de um paciente se a resistência do termistor nessa temperatura é 82,0% de seu valor em\(\displaystyle 37.0ºC\) (temperatura corporal normal)?
(b) O valor negativo para α tamanho 12 {α} {} pode não ser mantido para temperaturas muito baixas. Discuta o porquê e se esse é o caso aqui. (Dica: a resistência não pode se tornar negativa.)
70. Conceitos integrados
(a) Refazer o exercício levando em consideração a expansão térmica do filamento de tungstênio. Você pode assumir um coeficiente de expansão térmica de\(\displaystyle 12×10^{−6}/ºC\).
(b) Em que porcentagem sua resposta difere da do exemplo?
Solução
(a)\(\displaystyle 4.7Ω\) (total)
(b) Redução de 3,0%
71. Resultados irracionais
(a) A que temperatura você deve elevar um resistor feito de constantan para dobrar sua resistência, assumindo um coeficiente de resistividade de temperatura constante?
(b) Para cortá-lo ao meio?
(c) O que não é razoável nesses resultados? (d) Quais suposições não são razoáveis ou quais premissas são inconsistentes?
20.4: Energia elétrica e energia
72. Qual é a potência de um\(\displaystyle 1.00×10^2MV\) raio com uma corrente de\(\displaystyle 2.00 × 10^4A\)?
Solução
\(\displaystyle 2.00×10^{12}W\)
73. Que energia é fornecida ao motor de partida de um caminhão grande que consome 250 A de corrente de uma conexão de bateria de 24,0 V?
74. Uma carga de 4,00 C de carga passa pelas células solares de uma calculadora de bolso em 4,00 h. Qual é a potência de saída, dado que a saída de tensão da calculadora é de 3,00 V? (Veja a Figura.)

A faixa de células solares logo acima das teclas desta calculadora converte luz em eletricidade para suprir suas necessidades de energia. (crédito: Evan-Amos, Wikimedia Commons)
75. Quantos watts uma lanterna que\(\displaystyle 6.00×10^2C\) passou por ela em 0,500 h usa se sua voltagem for de 3,00 V?
76. Encontre a energia dissipada em cada um desses cabos de extensão:
(a) um cabo de extensão com uma\(\displaystyle 0.0600-Ω\) resistência e através do qual flui 5,00 A;
(b) um cabo mais barato utilizando fio mais fino e com uma resistência de\(\displaystyle 0.300Ω.\)
Solução
(a) 1,50 W
(b) 7,50 W
77. Verifique se as unidades de um volt-ampere são watts, conforme implícito na equação\(\displaystyle P=IV\).
78. Mostre que as unidades\(\displaystyle 1V^2/Ω=1W \), conforme implícito na equação\(\displaystyle P=V^2/R\).
Solução
\(\displaystyle \frac{V^2}{Ω}=\frac{V^2}{V/A}=AV=(\frac{C}{s})(\frac{J}{C})=\frac{J}{s}=1W\)
79. Mostre que as unidades\(\displaystyle 1A^2⋅Ω=1W\), conforme implícito na equação\(\displaystyle P=I^2R\).
80. Verifique a equivalência da unidade de energia que\(\displaystyle 1kW⋅h = 3.60×10^6J\).
Solução
\(\displaystyle 1kW⋅h=(\frac{1×10^3J}{1 s})(1 h)(\frac{3600s}{1h})=3.60×10^6J\)
81. Os elétrons em um tubo de raios-X são acelerados\(\displaystyle 1.00×10^2kV\) e direcionados em direção a um alvo para produzir raios-X. Calcule a potência do feixe de elétrons neste tubo se ele tiver uma corrente de 15,0 mA.
82. Um aquecedor elétrico de água consome 5,00 kW por 2,00 h por dia. Qual é o custo de operá-lo por um ano se os custos de eletricidade\(\displaystyle 12.0 cents/kW⋅h\)? Veja a Figura.

Aquecedor elétrico de água quente sob demanda. O calor é fornecido à água somente quando necessário. (crédito: aviddavid, Flickr)
Solução:
$438/ano
83. Com uma torradeira de 1200 W, quanta energia elétrica é necessária para fazer uma fatia de torrada (tempo de cozimento = 1 minuto)? Em\(\displaystyle 9.0 cents/kW ⋅ h\), quanto isso custa?
84. Qual seria o custo máximo de uma CFL de forma que o custo total (investimento mais operação) fosse o mesmo tanto para lâmpadas CFL quanto para lâmpadas incandescentes de 60 W? Suponha que o custo da lâmpada incandescente seja de 25 centavos e que os custos de eletricidade\(\displaystyle 10 cents/kWh\). Calcule o custo por 1000 horas, como no exemplo de custo-benefício do CFL.
Solução
$6,25
85. Algumas marcas de carros mais antigos têm sistemas elétricos de 6,00 V.
(a) Qual é a resistência ao calor de um farol de 30,0 W em um carro desse tipo?
(b) Que corrente flui através dela?
86. As baterias alcalinas têm a vantagem de liberar tensão constante até quase o fim de sua vida útil. Por quanto tempo uma bateria alcalina de 1,58 V manterá uma lâmpada de lanterna de 1,00 W acesa?\(\displaystyle 1.00 A⋅h\)
Solução
1,58 h
87. Um cauterizador, usado para interromper o sangramento em cirurgia, produz 2,00 mA a 15,0 kV.
(a) Qual é a sua potência de saída?
(b) Qual é a resistência do caminho?
88. Diz-se que a televisão média está ligada 6 horas por dia. Estime o custo anual da eletricidade para operar 100 milhões de TVs, supondo que seu consumo de energia seja em média de 150 W e o custo médio da eletricidade\(\displaystyle 12.0cents/kW⋅h\).
Solução de
$3,94 bilhões/ano
89. Uma lâmpada antiga consome apenas 50,0 W, em vez de seus 60,0 W originais, devido ao afinamento evaporativo de seu filamento. Por qual fator seu diâmetro é reduzido, assumindo um afinamento uniforme ao longo de seu comprimento? Negligencie quaisquer efeitos causados pelas diferenças de temperatura.
90. O fio de cobre de calibre 00 tem um diâmetro de 9,266 mm. Calcule a perda de energia em um quilômetro desse fio quando ele carrega\(\displaystyle 1.00×10^2A\).
Solução
25,5 W
91. Conceitos integrados
Os vaporizadores frios passam uma corrente pela água, evaporando-a com apenas um pequeno aumento na temperatura. Um desses dispositivos domésticos é avaliado em 3,50 A e utiliza 120 V AC com 95,0% de eficiência.
(a) Qual é a taxa de vaporização em gramas por minuto?
(b) Quanta água você deve colocar no vaporizador durante 8,00 h de operação noturna? (Veja a Figura.)
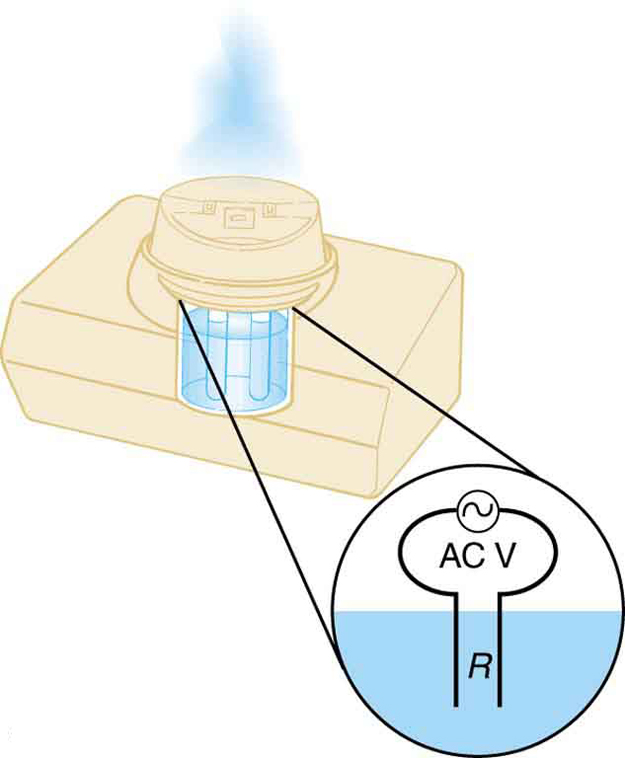
Este vaporizador frio passa a corrente diretamente pela água, vaporizando-a diretamente com relativamente pouco aumento de temperatura.
92. Conceitos integrados
(a) Que energia é dissipada por um raio com uma corrente de 20.000 A, uma tensão e um comprimento de 1,00 ms?\(\displaystyle 1.00×10^2MV\)
(b) Que massa de seiva de árvore poderia ser elevada\(\displaystyle 18.0ºC\) até o ponto de ebulição e depois evaporada por essa energia, supondo que a seiva tenha as mesmas características térmicas da água?
Solução
(a)\(\displaystyle 2.00×10^9J\)
(b) 769 kg
93. Conceitos integrados
Que corrente deve ser produzida por um aquecedor de biberões operado por bateria de 12,0 V para aquecer 75,0 g de vidro, 250 g de fórmula infantil e\(\displaystyle 3.00×10^2g\) de alumínio de\(\displaystyle 20.0ºC\) a\(\displaystyle 90.0ºC\) em 5,00 min?
94. Conceitos integrados
Quanto tempo é necessário para que um cauterizador cirúrgico aumente a temperatura de 1,00 g de tecido de 1\(\displaystyle 37.0ºC\) a 5\(\displaystyle 100ºC\) e depois ferva 0,500 g de água, se liberar 2,00 mA a 15,0 kV? Ignore a transferência de calor para os arredores.
Solução
45.0 s
95. Conceitos integrados
Os geradores hidrelétricos (veja a Figura) na Barragem Hoover produzem uma corrente máxima de\(\displaystyle 8.00×10^3A\) 250 kV.
(a) Qual é a potência de saída?
(b) A água que alimenta os geradores entra e sai do sistema em baixa velocidade (portanto, sua energia cinética não muda), mas perde 160 m de altitude. Quantos metros cúbicos por segundo são necessários, assumindo uma eficiência de 85,0%?

Geradores hidrelétricos na barragem de Hoover. (crédito: Jon Sullivan)
96. Conceitos integrados
Supondo uma eficiência de 95,0% para a conversão de energia elétrica pelo motor, qual corrente as baterias de 12,0 V de um carro elétrico de 750 kg devem ser capazes de fornecer:
(a) Acelerar do repouso até 25,0 m/s em 1,00 min?
(b) Escalar uma colina\(\displaystyle 2.00×10^2-m\) alta em 2,00 min a uma velocidade constante de 25,0 m/s enquanto exerce força para superar a resistência\(\displaystyle 5.00×10^2N\) do ar e o atrito?
(c) Viajar a uma velocidade constante de 25,0 m/s, exercendo uma\(\displaystyle 5.00×10^2N\) força para superar a resistência do ar e o atrito? Veja a Figura.

Esse ReVai, um carro elétrico, é recarregado em uma rua de Londres. (crédito: Frank Hebbert)
Solução
(a) 343 A
(b)\(\displaystyle 2.17×10^3A\)
(c)\(\displaystyle 1.10×10^3A\)
97. Conceitos integrados
Um trem suburbano leve consome 630 A de eletricidade de 650 V DC ao acelerar.
(a) Qual é a sua taxa de consumo de energia em quilowatts?
(b) Quanto tempo leva para atingir 20,0 m/s partindo do repouso se sua massa carregada for\(\displaystyle 5.30×10^4kg\), assumindo 95,0% de eficiência e potência constante?
(c) Encontre sua aceleração média.
(d) Discuta como a aceleração que você encontrou para o trem leve se compara à que pode ser típica de um automóvel.
98. Conceitos integrados
(a) Uma linha de transmissão de energia de alumínio tem uma resistência de\(\displaystyle 0.0580Ω/km\). Qual é sua massa por quilômetro?
(b) Qual é a massa por quilômetro de uma linha de cobre com a mesma resistência? Uma resistência menor reduziria o tempo de aquecimento. Discuta os limites práticos para acelerar o aquecimento diminuindo a resistência.
Solução
(a)\(\displaystyle 1.23×10^3kg\)
(b)\(\displaystyle 2.64×10^3kg\)
99. Conceitos integrados
(a) Um aquecedor de imersão que utiliza 120 V pode elevar a temperatura de um copo de alumínio de\(\displaystyle 1.00×10^2\) -g contendo 350 g de água de\(\displaystyle 20.0ºC\) até\(\displaystyle 95.0ºC\) 2,00 min. Encontre sua resistência, supondo que seja constante durante o processo.
(b) Uma resistência menor reduziria o tempo de aquecimento. Discuta os limites práticos para acelerar o aquecimento diminuindo a resistência.
100. Conceitos integrados
(a) Qual é o custo de aquecer uma banheira de hidromassagem contendo 1500 kg de água de\(\displaystyle 10.0ºC\) a\(\displaystyle 40.0ºC\), assumindo uma eficiência de 75,0% para contabilizar a transferência de calor para o ambiente? O custo da eletricidade é\(\displaystyle 9cents/kW⋅h\).
(b) Qual corrente foi usada pelo aquecedor elétrico de 220 V AC, se isso demorou 4,00 h?
101. Resultados irracionais
(a) Qual corrente é necessária para transmitir\(\displaystyle 1.00×10^2MW\) energia a 480 V?
(b) Qual energia é dissipada pelas linhas de transmissão se elas tiverem uma\(\displaystyle 1.00-Ω\) resistência?
(c) O que não é razoável nesse resultado?
(d) Quais suposições não são razoáveis ou quais premissas são inconsistentes?
Solução
(a)\(\displaystyle 2.08×10^5A\)
(b)\(\displaystyle 4.33×10^4MW\)
(c) As linhas de transmissão dissipam mais energia do que deveriam transmitir.
(d) Uma tensão de 480 V é excessivamente baixa para uma tensão de transmissão. As linhas de transmissão de longa distância são mantidas em tensões muito mais altas (geralmente centenas de quilovolts) para reduzir as perdas de energia.
102. Resultados irracionais
(a) Qual corrente é necessária para transmitir\(\displaystyle 1.00×10^2MW\) energia a 10,0 kV?
(b) Encontre a resistência de 1,00 km de fio que causaria uma perda de potência de 0,0100%.
(c) Qual é o diâmetro de um fio de cobre de 1,00 km de comprimento com essa resistência?
(d) O que não é razoável nesses resultados?
(e) Quais suposições não são razoáveis ou quais premissas são inconsistentes?
103. Construa seu próprio problema
Considere um aquecedor elétrico de imersão usado para aquecer uma xícara de água para fazer chá. Crie um problema no qual você calcule a resistência necessária do aquecedor para que ele aumente a temperatura da água e do copo em um período de tempo razoável. Também calcule o custo da energia elétrica usada em seu processo. Entre as coisas a serem consideradas estão a tensão usada, as massas e capacidades de calor envolvidas, as perdas de calor e o tempo durante o qual o aquecimento ocorre. Seu instrutor pode querer que você considere uma chave de segurança térmica (talvez bimetálica) que interromperá o processo antes que temperaturas prejudiciais sejam atingidas na unidade de imersão.
20.5: Corrente alternada versus corrente contínua
104. (a) Qual é a resistência ao calor de uma lâmpada de 25 W que funciona com 120 V AC?
(b) Se a temperatura de operação da lâmpada for\(\displaystyle 2700ºC\), qual é a sua resistência em\(\displaystyle 2600ºC\) `?
105. Certos equipamentos industriais pesados usam energia AC que tem uma tensão de pico de 679 V. Qual é a tensão rms?
Solução
480 V
106. Um determinado disjuntor dispara quando a corrente rms é de 15,0 A. Qual é a corrente de pico correspondente?
107. As aeronaves militares usam energia CA de 400 Hz, porque é possível projetar equipamentos mais leves nessa frequência mais alta. Qual é o tempo para um ciclo completo desse poder?
Solução
2,50 ms
108. Um turista norte-americano leva seu barbeador AC de 25,0 W e 120 V para a Europa, encontra um adaptador especial e o conecta a 240 V CA. Assumindo uma resistência constante, que energia a navalha consome ao ser arruinada?
109. Nesse problema, você verificará as declarações feitas no final das perdas de energia, por exemplo. (a) Qual corrente é necessária para transmitir 100 MW de potência a uma tensão de 25,0 kV? (b) Encontre a perda de potência em uma linha de transmissão 1,00 -Ω tamanho 12 {1 “.” “00"- %OMEGA} {}. (c) Que porcentagem de perda isso representa?
Solução
(a) 4,00 kA
(b) 16,0 MW
(c) 16,0%
110. Um pequeno ar condicionado para um prédio de escritórios opera com 408 V AC e consome 50,0 kW.
(a) Qual é sua resistência efetiva?
(b) Qual é o custo de operar o ar condicionado durante um mês quente de verão, quando ele está ligado 8,00 h por dia durante 30 dias e os custos de eletricidade\(\displaystyle 9.00 cents/kW⋅h\)?
111. Qual é o pico de consumo de energia de um forno micro-ondas de 120 V AC que consome 10,0 A?
Solução
2,40 kW
112. Qual é a corrente de pico através de um aquecedor de ambiente de 500 W que opera com alimentação de 120 V AC?
113. Dois dispositivos elétricos diferentes têm o mesmo consumo de energia, mas um deve ser operado em 120 V AC e o outro em 240 V AC.
(a) Qual é a proporção de suas resistências?
(b) Qual é a proporção de suas correntes?
(c) Supondo que sua resistência não seja afetada, por qual fator a potência aumentará se um dispositivo CA de 120 V for conectado a 240 V CA?
Solução
(a) 4,0
(b) 0,50
(c) 4,0
114. O fio de nicromo é usado em alguns aquecedores radiativos.
(a) Encontre a resistência necessária se a potência média de saída for de 1,00 kW utilizando 120 V AC.
(b) Qual comprimento de fio de nicromo, com uma área de seção transversal de\(\displaystyle 5.00mm^2\), é necessário se a temperatura de operação for\(\displaystyle 500º C\)?
(c) Que energia ele consumirá quando for ligado pela primeira vez?
115. Encontre o tempo após\(\displaystyle t=0\) o qual a tensão instantânea de 60 Hz AC atinge pela primeira vez os seguintes valores:
(uma)\(\displaystyle V_0/2\)
(b)\(\displaystyle V_0\)
(c) 0.
Solução
(a) 1,39 ms
(b) 4,17 ms
(c) 8,33 ms
116. (a) Em que duas vezes no primeiro período seguinte\(\displaystyle t=0\) a tensão instantânea em 60 Hz AC é igual\(\displaystyle V_{rms}\)?
(b)\(\displaystyle −V_{rms}\)?
20.6: Riscos elétricos e o corpo humano
117. (a) Quanta energia é dissipada em um curto-circuito de 240 V AC por meio de uma resistência de\(\displaystyle 0.250Ω\)?
(b) Quais fluxos de corrente?
Solução
(a) 230 kW
(b) 960 A
118. Qual voltagem está envolvida em um curto-circuito de 1,44 kW por meio de uma\(\displaystyle 0.100-Ω\) resistência?
119. Encontre a corrente através de uma pessoa e identifique o provável efeito nela se ela tocar em uma fonte CA de 120 V
(a) se ela estiver de pé sobre um tapete de borracha e oferecer uma resistência total de\(\displaystyle 300 kΩ\);
(b) se ela estiver descalça na grama molhada e tiver uma resistência de apenas\(\displaystyle 4000 kΩ\).
Solução
(a) 0,400 mA, sem efeito
(b) 26,7 mA, contração muscular durante o choque (não consigo desistir)
120. Enquanto toma banho, uma pessoa toca na caixa metálica de um rádio. O caminho através da pessoa até o cano de drenagem e o solo tem uma resistência de\(\displaystyle 4000Ω\). Qual é a menor voltagem na caixa do rádio que pode causar fibrilação ventricular?
121. Tentando tolamente pescar um pedaço de pão queimado em uma torradeira com uma faca de manteiga de metal, um homem entra em contato com 120 V AC. Ele nem sente isso, pois, felizmente, está usando sapatos com sola de borracha. Qual é a resistência mínima do caminho que a corrente segue através da pessoa?
Solução
\(\displaystyle 1.20×10^5Ω\)
122. (a) Durante a cirurgia, uma corrente tão pequena quanto\(\displaystyle 20.0 μA\) aplicada diretamente no coração pode causar fibrilação ventricular. Se a resistência do coração exposto for\(\displaystyle 300Ω\), qual é a menor voltagem que representa esse perigo?
(b) Sua resposta implica que são necessárias precauções especiais de segurança elétrica?
123. (a) Qual é a resistência de um curto-circuito de 220 V AC que gera uma potência de pico de 96,8 kW?
(b) Qual seria a potência média se a tensão fosse de 120 V AC?
Solução
(a)\(\displaystyle 1.00Ω\)
(b) 14,4 kW
124. Um desfibrilador cardíaco passa 10,0 A pelo torso do paciente por 5,00 ms na tentativa de restaurar o batimento normal.
(a) Quanta cobrança foi aprovada?
(b) Qual voltagem foi aplicada se 500 J de energia fossem dissipados?
(c) Qual foi a resistência do caminho?
(d) Encontre o aumento de temperatura causado nos 8,00 kg de tecido afetado.
125. Conceitos integrados
Um curto-circuito em um cabo de aparelho de 120 V tem uma\(\displaystyle 0.500-Ω\) resistência. Calcule o aumento de temperatura de 2,00 g de materiais circundantes, assumindo que sua capacidade térmica específica é\(\displaystyle 0.200cal/g⋅ºC\) e que são necessários 0,0500 s para um disjuntor interromper a corrente. É provável que isso seja prejudicial?
A
temperatura da solução aumenta\(\displaystyle 860º C\). É muito provável que seja prejudicial.
126. Construa seu próprio problema
Considere uma pessoa trabalhando em um ambiente onde correntes elétricas podem passar por seu corpo. Crie um problema no qual você calcule a resistência do isolamento necessária para proteger a pessoa contra danos. Entre as coisas a serem consideradas estão a voltagem à qual a pessoa pode estar exposta, a provável resistência corporal (seca, úmida,...) e correntes aceitáveis (seguras, mas detectadas, seguras e não sentidas,...).
20.7: Condução nervosa — Eletrocardiogramas
127. Conceitos integrados
Use o ECG na Figura para determinar a frequência cardíaca em batimentos por minuto, assumindo um tempo constante entre os batimentos.
Solução
80 batimentos/minuto
128. Conceitos integrados
(a) Referindo-se à Figura, determine o tempo em que a pressão sistólica fica atrás do meio do complexo QRS.
(b) Discuta os motivos do intervalo de tempo.

