Skip to main content
Global

17.5: Interferência sonora e ressonância - ondas estacionárias em colunas de ar

  1. Last updated
  2. Save as PDF
  • Page ID
    194202

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Defina antinodo, nodo, fundamental, sobretons e harmônicos.
    • Identifique casos de interferência sonora em situações cotidianas.
    • Descreva como a interferência sonora que ocorre dentro de tubos abertos e fechados altera as características do som e como isso se aplica aos sons produzidos por instrumentos musicais.
    • Calcule o comprimento de um tubo usando medições de ondas sonoras.

    A interferência é a marca registrada das ondas, todas as quais exibem interferência construtiva e destrutiva exatamente análoga à observada nas ondas de água. Na verdade, uma forma de provar que algo “é uma onda” é observar os efeitos de interferência. Portanto, sendo o som uma onda, esperamos que ele exiba interferência; já mencionamos alguns desses efeitos, como as batidas de duas notas semelhantes tocadas simultaneamente.

    Fotografia de um par de fones de ouvido e do conector usado para conectá-lo ao sistema de som.
    Figura\(\PageIndex{1}\): Alguns tipos de fones de ouvido usam os fenômenos de interferência construtiva e destrutiva para cancelar ruídos externos. (crédito: JVC America, Flickr)

    A figura\(\PageIndex{2}\) mostra um uso inteligente da interferência sonora para cancelar o ruído. Aplicações em larga escala de redução ativa de ruído por interferência destrutiva são contempladas em compartimentos inteiros de passageiros em aeronaves comerciais. Para obter interferência destrutiva, uma análise eletrônica rápida é realizada e um segundo som é introduzido com seus máximos e mínimos exatamente invertidos do ruído de entrada. As ondas sonoras em fluidos são ondas de pressão e consistentes com o princípio de Pascal; pressões de duas fontes diferentes somam e subtraem como números simples; ou seja, pressões manométricas positivas e negativas aumentam a pressão, produzindo um som de menor intensidade. Embora a interferência completamente destrutiva seja possível somente nas condições mais simples, é possível reduzir os níveis de ruído em 30 dB ou mais usando essa técnica.

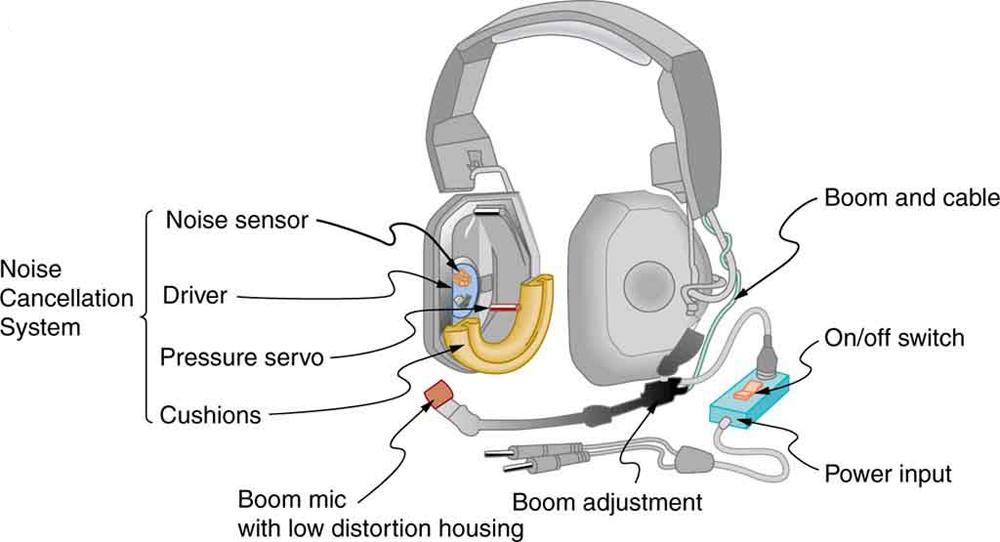
    Uma imagem detalhada dos fones de ouvido com todas as suas partes rotuladas. Ele mostra o sistema de cancelamento de ruído em ambos os tampões de ouvido que consistem no sensor de ruído, driver, servo de pressão e almofadas. Há um microfone de lança com caixa de baixa frequência, um ajuste de lança, lança e cabo, todos conectados a um lado do cabo de entrada de energia. É mostrado que o cabo de entrada de energia tem um botão liga/desliga.
    Figura\(\PageIndex{2}\): Fones de ouvido projetados para cancelar ruídos com interferência destrutiva criam uma onda sonora exatamente oposta ao som recebido. Esses fones de ouvido podem ser mais eficazes do que a simples atenuação passiva usada na maioria dos protetores de ouvido. Esses fones de ouvido foram usados no voo recorde, em todo o mundo, sem escalas da aeronave Voyager, para proteger a audição dos pilotos do ruído do motor.

    Onde mais podemos observar a interferência sonora? Todas as ressonâncias sonoras, como em instrumentos musicais, são devidas a interferências construtivas e destrutivas. Somente as frequências ressonantes interferem construtivamente para formar ondas estacionárias, enquanto outras interferem destrutivamente e estão ausentes. Do pé feito ao soprar sobre uma garrafa, ao sabor característico da caixa de som de um violino e à capacidade de reconhecimento da voz de um grande cantor, a ressonância e as ondas estacionárias desempenham um papel vital.

    Interferência

    A interferência é um aspecto tão fundamental das ondas que observar a interferência é a prova de que algo é uma onda. A natureza ondulatória da luz foi estabelecida por experimentos que mostraram interferência. Da mesma forma, quando elétrons espalhados pelos cristais exibiram interferência, sua natureza ondulatória foi confirmada como sendo exatamente a prevista pela simetria com certas características de onda da luz.

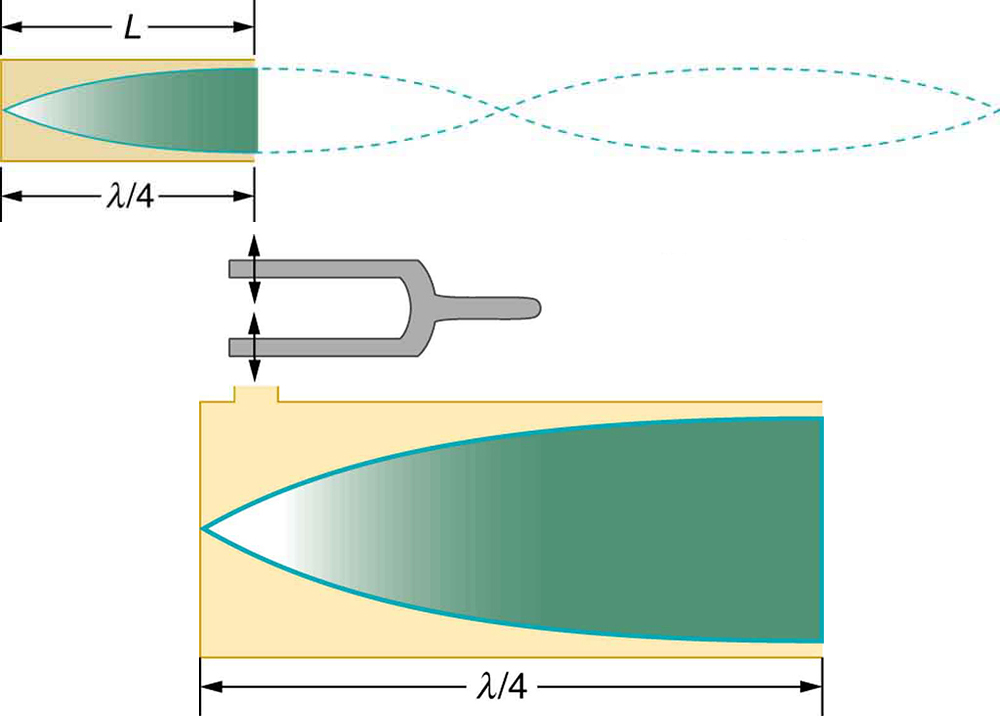
    Suponha que seguremos um diapasão próximo à extremidade de um tubo que está fechado na outra extremidade, conforme mostrado na Figura\(\PageIndex{3}\)\(\PageIndex{4}\), Figura\(\PageIndex{5}\), Figura e Figura\(\PageIndex{6}\). Se o diapasão tiver a frequência certa, a coluna de ar no tubo ressoa alto, mas na maioria das frequências ela vibra muito pouco. Essa observação significa apenas que a coluna de ar tem apenas certas frequências naturais. Os números mostram como uma ressonância na menor dessas frequências naturais é formada. Um distúrbio percorre o tubo na velocidade do som e ricocheteia pela extremidade fechada. Se o tubo tiver o comprimento certo, o som refletido volta ao diapasão exatamente meio ciclo depois e interfere construtivamente com o som contínuo produzido pelo diapasão. Os sons recebidos e refletidos formam uma onda estacionária no tubo, conforme mostrado.

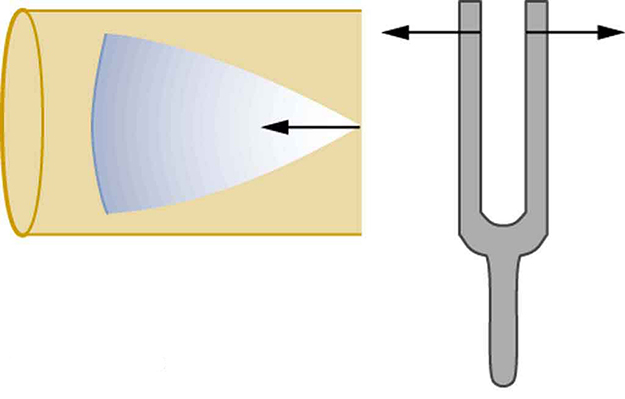
    O lado direito mostra um diapasão vibratório com o braço direito do garfo se movendo para a direita e o braço esquerdo se movendo para a esquerda. O lado esquerdo mostra um cone de ondas de ressonância se movendo através de um tubo da extremidade aberta até a extremidade fechada. A ponta do cone está na extremidade aberta do tubo.
    Figura\(\PageIndex{3}\): Ressonância do ar em um tubo fechado em uma extremidade, causada por um diapasão. Um distúrbio se move pelo tubo
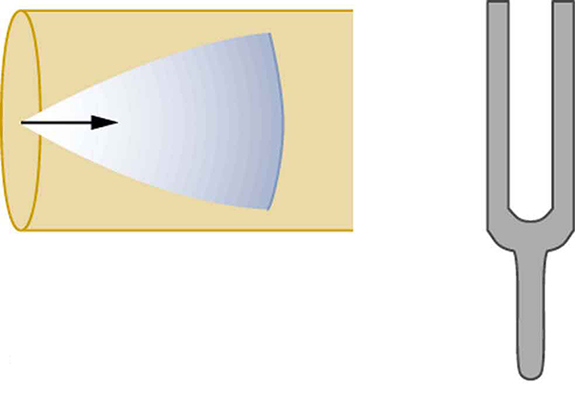
    O lado direito mostra um diapasão vibratório. O lado esquerdo mostra um cone de ondas de ressonância refletidas na extremidade fechada do tubo. A ponta do cone está na extremidade fechada do tubo e a boca do cone está se movendo em direção à extremidade aberta do tubo.
    Figura\(\PageIndex{4}\): Ressonância do ar em um tubo fechado em uma extremidade, causada por um diapasão. A perturbação é refletida na extremidade fechada do tubo.
    O lado esquerdo mostra um cone de ondas de ressonância refletidas na extremidade fechada do tubo. A boca do cone atingiu a extremidade aberta do tubo. O lado direito mostra um diapasão vibratório com o braço esquerdo do garfo se movendo para a direita e o braço direito se movendo para a esquerda.
    Figura\(\PageIndex{5}\): Ressonância do ar em um tubo fechado em uma extremidade, causada por um diapasão. Se o comprimento do tubo\(L\) estiver correto, a perturbação volta ao diapasão meio ciclo depois e interfere de forma construtiva com o som contínuo do diapasão. Essa interferência forma uma onda estacionária e a coluna de ar ressoa.
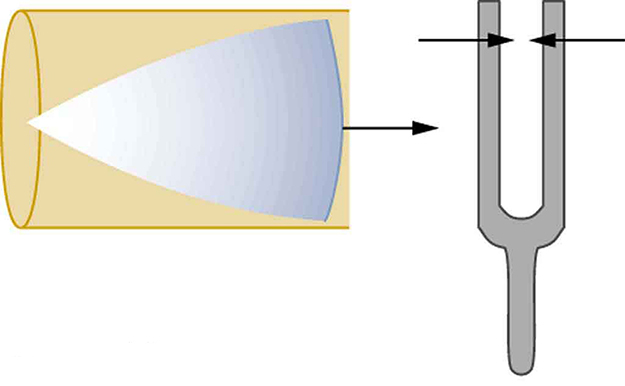
    O lado direito mostra um diapasão vibratório com o braço direito se movendo para a direita e o braço esquerdo se movendo para a esquerda. O lado esquerdo mostra um cone de ondas de ressonância refletidas na extremidade fechada do tubo. O lado curvo do cone atingiu o diapasão. O comprimento do tubo é dado como igual a lambda dividido por quatro.
    Figura\(\PageIndex{6}\): Ressonância do ar em um tubo fechado em uma extremidade, causada por um diapasão. Um gráfico do deslocamento do ar ao longo do comprimento do tubo não mostra nenhum na extremidade fechada, onde o movimento é restrito, e um máximo na extremidade aberta. Essa onda estacionária tem um quarto de seu comprimento de onda no tubo, de modo que\(\lambda = 4L\).

    A onda estacionária formada no tubo tem seu deslocamento máximo de ar (um antinodo) na extremidade aberta, onde o movimento é irrestrito, e nenhum deslocamento (um nó) na extremidade fechada, onde o movimento do ar é interrompido. A distância de um nó a um antinodo é um quarto do comprimento de onda, e isso é igual ao comprimento do tubo; portanto,\(\lambda = 4L\). Essa mesma ressonância pode ser produzida por uma vibração introduzida na extremidade fechada do tubo ou perto dela, conforme mostrado na Figura\(\PageIndex{7}\). É melhor considerar isso uma vibração natural da coluna de ar, independentemente de como ela é induzida.

    Um cone de ondas de ressonância refletido na extremidade fechada do tubo é mostrado. É mostrado que um diapasão vibra em uma pequena abertura acima da extremidade fechada do tubo. O comprimento do tubo L é dado como igual a lambda dividido por quatro.
    Figura\(\PageIndex{7}\): A mesma onda estacionária é criada no tubo por uma vibração introduzida perto de sua extremidade fechada.

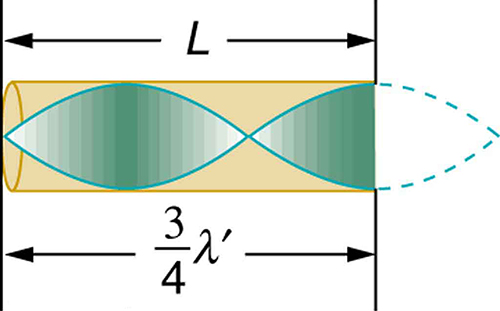
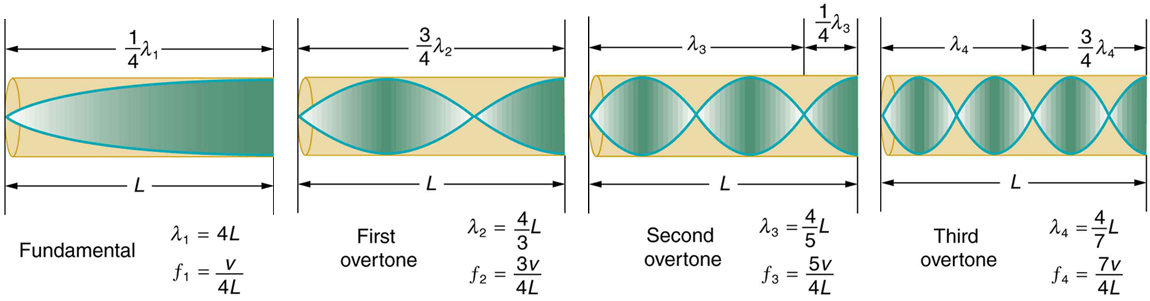
    Dado que deslocamentos máximos de ar são possíveis na extremidade aberta e nenhum na extremidade fechada, existem outros comprimentos de onda mais curtos que podem ressoar no tubo, como o mostrado na Figura\(\PageIndex{8}\). Aqui, a onda estacionária tem três quartos de seu comprimento de onda no tubo, ou seja\(L = (3/4) \lambda'\), assim\(\lambda' = 4L/3\). A continuação desse processo revela toda uma série de sons de menor comprimento de onda e frequência mais alta que ressoam no tubo. Usamos termos específicos para as ressonâncias em qualquer sistema. A frequência ressonante mais baixa é chamada de fundamental, enquanto todas as frequências ressonantes mais altas são chamadas de sobretons. Todas as frequências ressonantes são múltiplos integrais do fundamental e são chamadas coletivamente de harmônicas. O fundamental é o primeiro harmônico, o primeiro tom é o segundo harmônico e assim por diante. A figura\(\PageIndex{9}\) mostra o fundamental e os três primeiros tons (os primeiros quatro harmônicos) em um tubo fechado em uma extremidade.

    Um cone de ondas de ressonância refletido na extremidade fechada do tubo é mostrado como uma onda. Há três quartos da onda dentro do tubo e um quarto externo mostrado como curva pontilhada. O comprimento do tubo é dado como três quartos vezes lambda prime.
    Figura\(\PageIndex{8}\): Outra ressonância para um tubo fechado em uma extremidade. Isso tem deslocamentos máximos de ar na extremidade aberta e nenhum na extremidade fechada. O comprimento de onda é menor, com três quartos\(\lambda'\) igualando o comprimento do tubo, de modo que\(\lambda' = 4L/3\). Essa vibração de alta frequência é o primeiro tom.
    Existem quatro tubos, cada um dos quais está fechado em uma extremidade. Cada tubo tem ondas de ressonância refletidas na extremidade fechada. No primeiro tubo, marcado como Fundamental, o comprimento de onda é longo e apenas um quarto da onda está dentro do tubo, com o deslocamento máximo de ar na extremidade aberta. No segundo tubo, marcado como Primeiro sobretom, o comprimento de onda é um pouco menor e três quartos da onda estão dentro do tubo, com o deslocamento máximo de ar na extremidade aberta. No terceiro tubo, marcado como Segundo sobretom, o comprimento de onda ainda é menor e um e um quarto da onda estão dentro do tubo, com o deslocamento máximo de ar na extremidade aberta. No quarto tubo, marcado como Terceiro tom, o comprimento de onda é menor que os outros, e um e três quartos da onda estão dentro do tubo, com o deslocamento máximo do ar na extremidade aberta.
    Figura\(\PageIndex{9}\): Os tons fundamentais e os três mais baixos de um tubo fechado em uma extremidade. Todos têm deslocamentos máximos de ar na extremidade aberta e nenhum na extremidade fechada.

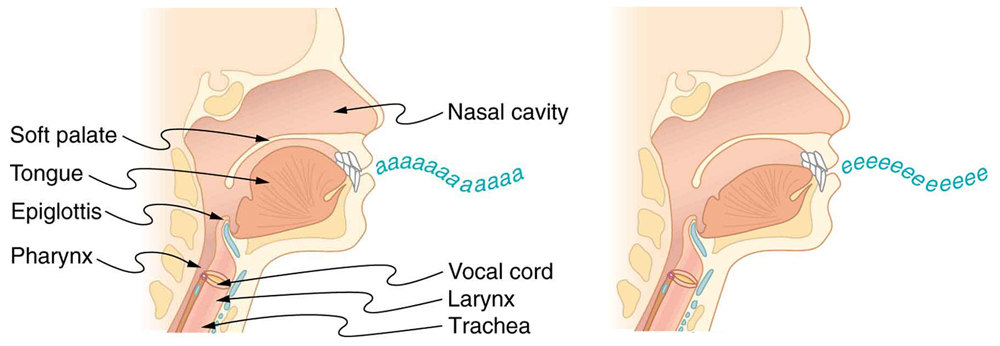
    O fundamental e os tons podem estar presentes simultaneamente em uma variedade de combinações. Por exemplo, o C médio em um trompete tem um som distintamente diferente do C médio em um clarinete, sendo ambos os instrumentos versões modificadas de um tubo fechado em uma extremidade. A frequência fundamental é a mesma (e geralmente a mais intensa), mas os tons e sua mistura de intensidades são diferentes e sujeitos ao sombreamento do músico. Essa mistura é o que dá a vários instrumentos musicais (e vozes humanas) suas características distintivas, sejam eles colunas de ar, cordas, caixas de som ou tambores. De fato, grande parte da nossa fala é determinada pela modelagem da cavidade formada pela garganta e pela boca e pelo posicionamento da língua para ajustar o fundamental e a combinação de conotações. Cavidades ressonantes simples podem ser feitas para ressoar com o som das vogais, por exemplo. (Veja a Figura\(\PageIndex{10}\).) Nos meninos, na puberdade, a laringe cresce e a forma da cavidade ressonante muda, dando origem à diferença nas frequências predominantes na fala entre homens e mulheres.

    Duas fotos da garganta e da boca em seção transversal são mostradas. A primeira foto tem partes da boca e da garganta marcadas. A primeira imagem mostra a posição da boca e da língua ao produzir um som a a a, e a segunda imagem mostra a posição da boca e da língua ao produzir um som e e e.
    Figura\(\PageIndex{10}\): A garganta e a boca formam uma coluna de ar fechada em uma extremidade que ressoa em resposta às vibrações na caixa de voz. O espectro de sobretons e suas intensidades variam com o formato da boca e a posição da língua para formar sons diferentes. A caixa de voz pode ser substituída por um vibrador mecânico e uma fala compreensível ainda é possível. Variações nas formas básicas tornam diferentes vozes reconhecíveis.

    Agora, vamos procurar um padrão nas frequências ressonantes para um tubo simples que está fechado em uma extremidade. O fundamental tem\(\lambda = 4L\) e a frequência estão relacionados ao comprimento de onda e à velocidade do som, conforme dado por:

    \[v_w = f\lambda.\]

    Resolver para\(f\) nesta equação dá

    \[f = \dfrac{v_w}{\lambda} = \dfrac{v_w}{4L},\]

    onde\(v_w\) está a velocidade do som no ar. Da mesma forma, o primeiro tom tem\(\lambda' = 4L/3\) (veja a Figura\(\PageIndex{9}\)), de modo que

    \[f' = 3\dfrac{v_w}{4L} = 3f.\]

    Porque\(f' = 3f\) chamamos o primeiro tom de terceiro harmônico. Continuando esse processo, vemos um padrão que pode ser generalizado em uma única expressão. As frequências ressonantes de um tubo fechado em uma extremidade são

    \[f_n = n\dfrac{v_w}{4L}, \, n = 1, \, 3,\space 5,\]

    onde\(f_1\) está o fundamental,\(f_3\) é o primeiro tom, e assim por diante. É interessante que as frequências ressonantes dependam da velocidade do som e, portanto, da temperatura. Essa dependência representa um problema perceptível para os órgãos em antigas catedrais sem aquecimento, e também é a razão pela qual os músicos geralmente levam seus instrumentos de sopro à temperatura ambiente antes de tocá-los.

    Exemplo\(\PageIndex{1}\): Find the Length of a Tube with a 128 Hz Fundamental

    1. Qual o comprimento de um tubo fechado em uma extremidade em um dia em que a temperatura do ar deve ter\(22^oC\), se sua frequência fundamental for 128 Hz (C abaixo do meio C)?
    2. Qual é a frequência de seu quarto tom?

    Estratégia

    A duração\(L\) pode ser encontrada a partir do relacionamento em\(f_n = n\frac{v_w}{4L}\), mas primeiro precisamos encontrar a velocidade do som\(v_w\).

    Solução para (a)

    (1) Identifique conhecidos:

    • a frequência fundamental é 128 Hz
    • a temperatura do ar é\(22^oC\)

    (2) Use\(f_n = n\frac{v_w}{4L}\) para encontrar a frequência fundamental (n = 1). \[f_1 = \dfrac{v_w}{4L}\]

    (3) Resolva essa equação para o comprimento. \[L = \dfrac{v_w}{4f_1}\]

    (4) Encontre a velocidade do som usando\(v_w = (331 \, m/s)\sqrt{\frac{T}{273 \, K}}\). \[v_w = (331 \, m/s)\sqrt{\dfrac{295 \, K}{273 \, K}} = 344 \, m/s\]

    (5) Insira os valores da velocidade do som e da frequência na expressão para\(L\). \[L = \dfrac{v_w}{4f_1} = \dfrac{344 \, m/s}{4(128 \, Hz)} = 0.672 \, m\]

    Discussão sobre (a)

    Muitos instrumentos de sopro são tubos modificados que têm orifícios para os dedos, válvulas e outros dispositivos para alterar o comprimento da coluna de ar ressonante e, portanto, a frequência da nota tocada. Os chifres que produzem frequências muito baixas, como as tubas, requerem tubos tão longos que sejam enrolados em laços.

    Solução para (b)

    (1) Identifique conhecidos:

    • o primeiro tom tem\(n = 3\)
    • o segundo tom tem\(n = 5\)
    • o terceiro tom tem\(n = 7\)
    • o quarto tom tem\(n = 9\)

    (2) Insira o valor do quarto tom em\(f_n = n\frac{v_w}{4L}\). \[f_9 = 9\dfrac{v_w}{4L} = 9f_1 = 1.15 \, kHz\]

    Discussão sobre (b)

    Se esse tom ocorre em um tubo simples ou em um instrumento musical depende de como ele é estimulado a vibrar e dos detalhes de sua forma. O trombone, por exemplo, não produz sua frequência fundamental e apenas produz conotações.

    Outro tipo de tubo é aquele que está aberto nas duas extremidades. Exemplos são alguns tubos de órgão, flautas e oboés. As ressonâncias dos tubos abertos nas duas extremidades podem ser analisadas de forma muito semelhante às dos tubos fechados em uma extremidade. As colunas de ar em tubos abertos em ambas as extremidades têm deslocamentos máximos de ar em ambas as extremidades, conforme ilustrado na Figura\(\PageIndex{11}\). Ondas estacionárias se formam conforme mostrado.

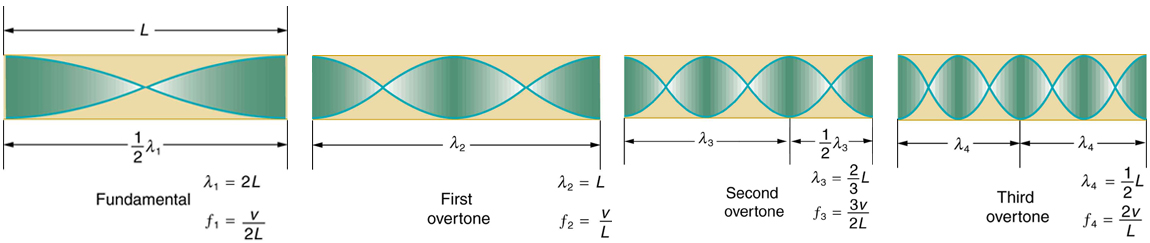
    As ondas de frequência ressonante em um tubo aberto nas duas extremidades são mostradas. Há um conjunto de quatro imagens. A primeira imagem mostra um tubo de comprimento L marcado como fundamental com meia onda. Os máximos das vibrações estão nas duas extremidades abertas do tubo. A segunda imagem mostra um tubo de comprimento L marcado primeiro sobre o tom com uma onda completa. Os máximos das vibrações estão nas duas extremidades abertas do tubo. A terceira imagem mostra um tubo de comprimento L marcado em segundo tom com uma onda completa e meia. Os máximos das vibrações estão nas duas extremidades abertas do tubo. A quarta imagem mostra um tubo de comprimento L marcado como terceiro sobre o tom com duas ondas completas. Os máximos das vibrações estão nas duas extremidades abertas do tubo.
    Figura\(\PageIndex{11}\): As frequências ressonantes de um tubo aberto em ambas as extremidades são mostradas, incluindo os três primeiros tons fundamentais e os três primeiros. Em todos os casos, os deslocamentos máximos de ar ocorrem em ambas as extremidades do tubo, dando-lhe frequências naturais diferentes das de um tubo fechado em uma extremidade.

    Com base no fato de que um tubo aberto em ambas as extremidades tem deslocamentos máximos de ar em ambas as extremidades, e usando a Figura\(\PageIndex{11}\) como guia, podemos ver que as frequências de ressonância de um tubo aberto em ambas as extremidades são:\[f_n = n\dfrac{v_w}{2L}, \, n = 1, \, 2, \, 3...,\] onde\(f_1\) é fundamental,\(f_2\) é o sobretom,\(f_3\) é o segundo sobretom, e assim por diante. Observe que um tubo aberto em ambas as extremidades tem uma frequência fundamental duas vezes maior do que teria se fosse fechado em uma extremidade. Ele também tem um espectro diferente de sobretons do que um tubo fechado em uma extremidade. Então, se você tivesse dois tubos com a mesma frequência fundamental, mas um estava aberto nas duas extremidades e o outro fechado em uma extremidade, eles soariam diferentes quando tocados porque têm conotações diferentes. O C médio, por exemplo, soaria mais rico tocado em um tubo aberto, porque tem múltiplos pares do fundamental e ímpar. Um tubo fechado tem apenas múltiplos ímpares.

    APLICAÇÕES DO MUNDO REAL: RESSONÂNCIA NO COTIDIANO

    A ressonância ocorre em muitos sistemas diferentes, incluindo cordas, colunas de ar e átomos. A ressonância é a oscilação acionada ou forçada de um sistema em sua frequência natural. Na ressonância, a energia é transferida rapidamente para o sistema oscilante e a amplitude de suas oscilações aumenta até que o sistema não possa mais ser descrito pela lei de Hooke. Um exemplo disso é o som distorcido produzido intencionalmente em certos tipos de rock.

    Os instrumentos de sopro usam ressonância nas colunas de ar para amplificar os tons produzidos pelos lábios ou palhetas vibrantes. Outros instrumentos também usam ressonância de ar de forma inteligente para amplificar o som. \(\PageIndex{12}\)A figura mostra um violino e uma guitarra, ambos com caixas de som, mas com formas diferentes, resultando em diferentes estruturas de sobretons. A corda vibrante cria um som que ressoa na caixa de som, amplificando bastante o som e criando conotações que dão ao instrumento seu sabor característico. Quanto mais complexo for o formato da caixa de ressonância, maior será sua capacidade de ressoar em uma ampla faixa de frequências. A marimba, como a mostrada na Figura,\(\PageIndex{13}\) usa panelas ou cabaças abaixo das ripas de madeira para amplificar seus tons. A ressonância da panela pode ser ajustada adicionando água.

    A primeira fotografia é de uma pessoa tocando violão e a segunda foto é de um violino.
    Figura\(\PageIndex{12}\): Instrumentos de cordas, como violinos e violões, usam ressonância em suas caixas de som para amplificar e enriquecer o som criado por suas cordas vibrantes. A ponte e os suportes acoplam as vibrações das cordas às caixas de sondagem e ao ar interno. (créditos: violão, Feliciano Guimares, Fotopedia; violino, Steve Snodgrass, Flickr)
    Fotografia de duas pessoas tocando marimba com cabaças como câmaras de ressonância.
    Figura\(\PageIndex{13}\): A ressonância tem sido usada em instrumentos musicais desde os tempos pré-históricos. Essa marimba usa cabaças como câmaras de ressonância para amplificar seu som. (crédito: APC Events, Flickr)

    Nós enfatizamos as aplicações do som em nossas discussões sobre ressonância e ondas estacionárias, mas essas ideias se aplicam a qualquer sistema que tenha características de onda. As cordas vibratórias, por exemplo, são realmente ressonantes e têm fundamentos e conotações semelhantes aos das colunas de ar. Mais sutis são as ressonâncias nos átomos devido ao caráter ondulatório de seus elétrons. Seus orbitais podem ser vistos como ondas estacionárias, que têm um estado fundamental (estado fundamental) e conotações (estados excitados). É fascinante que as características das ondas se apliquem a uma ampla variedade de sistemas físicos.

    Exercício\(\PageIndex{1}\)

    Descreva como os fones de ouvido com cancelamento de ruído diferem dos fones de ouvido padrão usados para bloquear sons externos.

    Resposta

    Os fones de ouvido comuns bloqueiam apenas as ondas sonoras com uma barreira física. Os fones de ouvido com cancelamento de ruído usam interferência destrutiva para reduzir o volume dos sons externos.

    Exercício\(\PageIndex{2}\)

    Como é possível usar o nó e o antinodo de uma onda estacionária para determinar o comprimento de um tubo de extremidade fechada?

    Resposta

    Quando o tubo ressoa em sua frequência natural, o nó da onda está localizado na extremidade fechada do tubo e o antinodo está localizado na extremidade aberta. O comprimento do tubo é igual a um quarto do comprimento de onda dessa onda. Assim, se soubermos o comprimento de onda da onda, podemos determinar o comprimento do tubo.

    EXPLORAÇÕES PHET: SOM

    Essa simulação permite que você veja as ondas sonoras. Ajuste a frequência ou o volume e você poderá ver e ouvir como a onda muda. Mova a ouvinte e ouça o que ela ouve.

    Resumo

    • A interferência sonora e a ressonância têm as mesmas propriedades definidas para todas as ondas.
    • Nas colunas de ar, a ressonância de frequência mais baixa é chamada de fundamental, enquanto todas as frequências ressonantes mais altas são chamadas de sobretons. Coletivamente, eles são chamados de harmônicos.
    • As frequências ressonantes de um tubo fechado em uma extremidade são:\(f_n = n\dfrac{v_w}{4L}, \, n = 1, \, 3, \, 5...,\)\(f_1\) é fundamental e\(L\) é o comprimento do tubo.
    • As frequências de ressonância de um tubo aberto em ambas as extremidades são:\(f_n = n\dfrac{v_w}{2L}, \, n = 1, \, 2, \, 3...\)

    Glossário

    antinodo
    ponto de deslocamento máximo
    nó
    ponto de deslocamento zero
    fundamental
    a ressonância de frequência mais baixa
    conotações
    todas as frequências ressonantes superiores às fundamentais
    harmônicos
    o termo usado para se referir coletivamente ao fundamental e suas conotações