16.1: Lei de Hooke - Estresse e tensão revisitados

Last updated
Save as PDF

Page ID: 194511

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Explique a terceira lei do movimento de Newton com relação à tensão e à deformação.
Descreva a restauração da força e do deslocamento.
Calcule a energia na Lei de Deformação de Hook e a energia armazenada em uma corda.

A primeira lei de Newton implica que um objeto oscilando para frente e para trás está experimentando forças. Sem força, o objeto se moveria em linha reta a uma velocidade constante em vez de oscilar. Considere, por exemplo, arrancar uma régua de plástico para a esquerda, conforme mostrado na Figura\(\PageIndex{1}\). A deformação da régua cria uma força na direção oposta, conhecida como força restauradora. Uma vez liberada, a força restauradora faz com que a régua volte para sua posição de equilíbrio estável, onde a força total sobre ela é zero. No entanto, quando a régua chega lá, ela ganha impulso e continua se movendo para a direita, produzindo a deformação oposta. Em seguida, é forçado para a esquerda, retornando ao equilíbrio, e o processo é repetido até que as forças dissipativas amortecam o movimento. Essas forças removem a energia mecânica do sistema, reduzindo gradualmente o movimento até que a régua descanse.

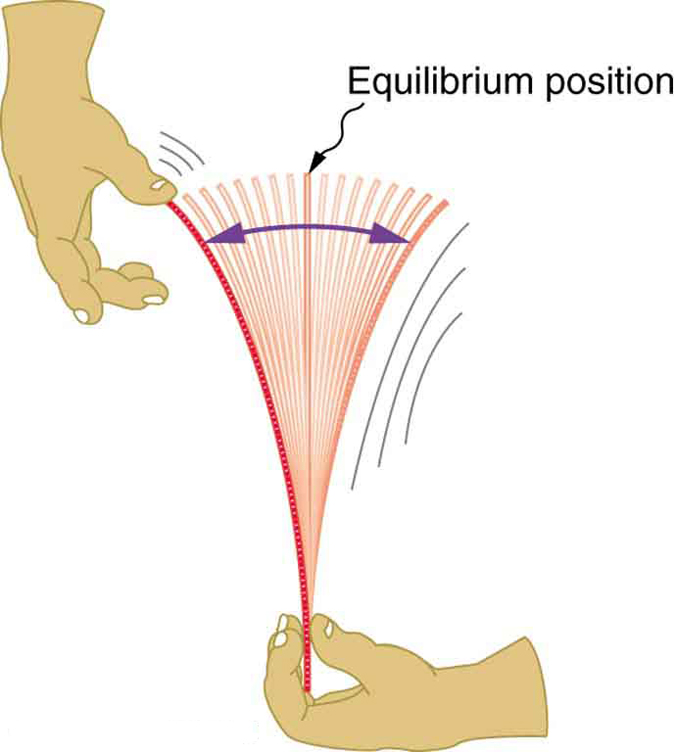
Nesta figura, uma mão segurando uma régua firmemente na parte inferior é mostrada. A outra mão puxa a parte superior da régua e depois a solta. Em seguida, a régua começa a vibrar e oscila em torno da posição de equilíbrio. Uma linha vertical é mostrada para marcar a posição de equilíbrio. Uma seta curva de duas pontas mostra a extensão da oscilação. — Figura\(\PageIndex{1}\): Quando deslocada de sua posição de equilíbrio vertical, essa régua de plástico oscila para frente e para trás devido à força restauradora que se opõe ao deslocamento. Quando a régua está à esquerda, há uma força à direita e vice-versa.

As oscilações mais simples ocorrem quando a força de restauração é diretamente proporcional ao deslocamento. Quando o estresse e a tensão foram abordados na Terceira Lei do Movimento de Newton, o nome dado a essa relação entre força e deslocamento foi a lei de Hooke:

\[F = -kx\]

Aqui,\(F\) está a força restauradora,\(x\) é o deslocamento do equilíbrio ou da deformação e\(k\) é uma constante relacionada à dificuldade de deformar o sistema. O sinal de menos indica que a força de restauração está na direção oposta ao deslocamento.

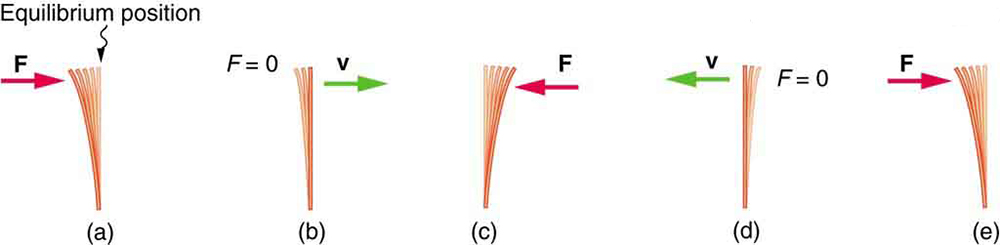
Uma série de ilustrações de réguas vibratórias de plástico é mostrada demonstrando a lei de Hooke. — Figura\(\PageIndex{2}\): (a) A régua de plástico foi liberada e a força restauradora está retornando a régua à sua posição de equilíbrio. (b) A força líquida é zero na posição de equilíbrio, mas a régua tem impulso e continua se movendo para a direita. (c) A força restauradora está na direção oposta. Ele para a régua e a move de volta ao equilíbrio novamente. (d) Agora, o governante tem impulso para a esquerda. (e) Na ausência de amortecimento (causado por forças de atrito), a régua atinge sua posição original. A partir daí, o movimento se repetirá.

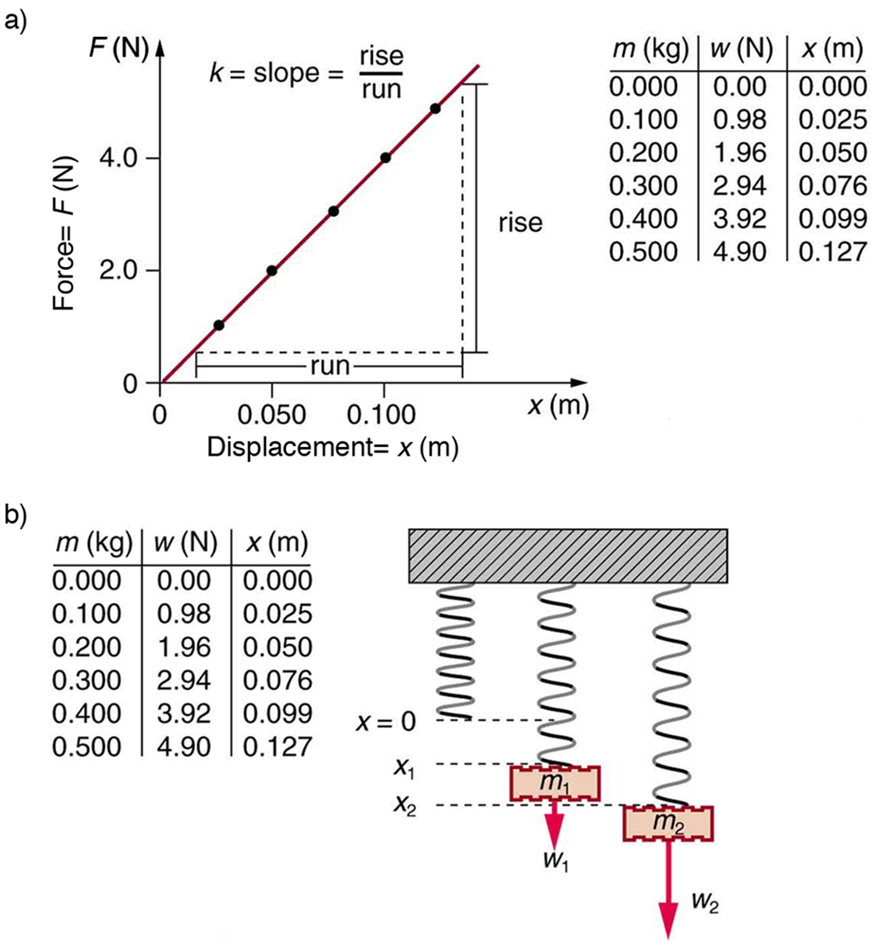
A constante de força\(k\) está relacionada à rigidez (ou rigidez) de um sistema — quanto maior a constante de força, maior a força de restauração e mais rígido é o sistema. As unidades de\(k\) são newtons por metro (N/m). Por exemplo,\(k\) está diretamente relacionado ao módulo de Young quando esticamos uma corda. A figura\(\PageIndex{3}\) mostra um gráfico do valor absoluto da força de restauração versus o deslocamento de um sistema que pode ser descrito pela lei de Hooke — uma simples mola neste caso. A inclinação do gráfico é igual à força constante\(k\) em newtons por metro. Um exercício comum de laboratório de física é medir as forças de restauração criadas pelas molas, determinar se elas seguem a lei de Hooke e calcular suas constantes de força, se o fizerem.

A figura a dada é o gráfico da força de restauração versus deslocamento. O deslocamento é dado por x em metros ao longo do eixo x, com escalas de zero até o ponto zero cinco zero, depois para o ponto um zero e depois para frente. A força de restauração é dada por F em unidade newton ao longo do eixo y, com escalas de zero a dois pontos zero a quatro pontos zero para frente. A linha do gráfico começa do zero e vai para cima até o ponto em que x é maior que o ponto um zero e F é maior que quatro pontos zero com pontos de interseção em distâncias iguais na linha inclinada. A inclinação é representada por K, que é dada pela elevação ao longo do eixo y após a corrida ao longo do eixo x. Os valores de massa em quilograma, peso em newtons e deslocamento em metros são dados junto com o gráfico em formato tabular. Na figura b, uma barra de peso horizontal é mostrada com três molas de medição de peso amarradas à sua parte inferior, penduradas na direção vertical descendente. A primeira barra não tem massa pendurada nela, mostrando deslocamento zero, pois x é igual a zero. É a mola menos esticada para baixo. A segunda mola tem a massa m um amarrada a ela, o que exerce uma força w um, na mola, o que causa o deslocamento na mola mostrada aqui como x um. Da mesma forma, a terceira mola é mais esticada para baixo com uma massa m dois pendurada nela com força w dois e deslocamento x dois. Os valores de massa em kg, peso em newtons e deslocamento em metros são dados com o gráfico em formato tabular. — Figura\(\PageIndex{3}\): (a) Um gráfico do valor absoluto da força de restauração versus deslocamento é exibido. O fato de o gráfico ser uma linha reta significa que o sistema obedece à lei de Hooke. A inclinação do gráfico é a força constante\(k\). (b) Os dados no gráfico foram gerados medindo o deslocamento de uma mola do equilíbrio enquanto suportava vários pesos. A força de restauração é igual ao peso suportado, se a massa estiver estacionária.

Exemplo\(\PageIndex{1}\): How Stiff Are Car Springs?

Qual é a força constante para o sistema de suspensão de um carro que assenta 1,20 cm quando uma pessoa de 80,0 kg entra?

A figura mostra o lado esquerdo da área traseira de um carro hatchback, mostrando a fonte da roda traseira. Há uma flecha na estrada apontando sua cabeça em direção a esta roda. — Figura\(\PageIndex{4}\): A massa de um carro aumenta devido à introdução de um passageiro. Isso afeta o deslocamento do carro em seu sistema de suspensão. (crédito: exfordy no Flickr)

Estratégia

Considere que o carro está em sua posição de equilíbrio\(x = 0\) antes de a pessoa entrar. O carro então se acomoda 1,20 cm, o que significa que ele é deslocado para uma posição\(x = -1.20 \times 10^{-2} m\). Nesse ponto, as molas fornecem uma força restauradora\(F\) igual ao peso da pessoa.\(w = mg = (80.0 \, kg)(9.80 \, m/s^2) = 784 \, N.\) Consideramos que essa força está\(F\) na lei de Hooke. Conhecendo\(F\) e\(x\), podemos então resolver a constante de força\(k\).

Solução

1. Resolva a lei de Hooke,\(F = -kx\), para\(k\):

\[k = -\dfrac{F}{x}. \nonumber\]

2. Substitua valores conhecidos e resolva\(k\):

\[\begin{align*} k &= -\dfrac{784 \, N}{-1.20 \times 10^{-2}m} \\[5pt] &=6.53 \times 10^4 \, N/m.\end{align*}\]

Discussão

Observe isso\(F\) e\(x\) tenha sinais opostos porque eles estão em direções opostas — a força de restauração aumenta e o deslocamento diminui. Além disso, observe que o carro oscilaria para cima e para baixo quando a pessoa entrasse se não fosse para amortecimento (devido às forças de atrito) fornecidas pelos amortecedores. Carros saltitantes são um sinal claro de amortecedores ruins.

Energia na Lei da Deformação de Hooke

Para produzir uma deformação, o trabalho deve ser feito. Ou seja, uma força deve ser exercida à distância, seja você puxando uma corda de violão ou comprimindo uma mola de carro. Se o único resultado for deformação e nenhum trabalho for transformado em energia térmica, sonora ou cinética, todo o trabalho é inicialmente armazenado no objeto deformado como alguma forma de energia potencial. A energia potencial armazenada em uma fonte é\(PE_{el} = \dfrac{1}{2}kx^2\). Aqui, generalizamos a ideia de energia potencial elástica para uma deformação de qualquer sistema que possa ser descrita pela lei de Hooke. Conseqüentemente,

\[PE_{el} = \dfrac{1}{2}kx^2,\]

onde\(PR_{el}\) está a energia potencial elástica armazenada em qualquer sistema deformado que obedeça à lei de Hooke e tenha um deslocamento\(x\) do equilíbrio e uma força constante\(k\).

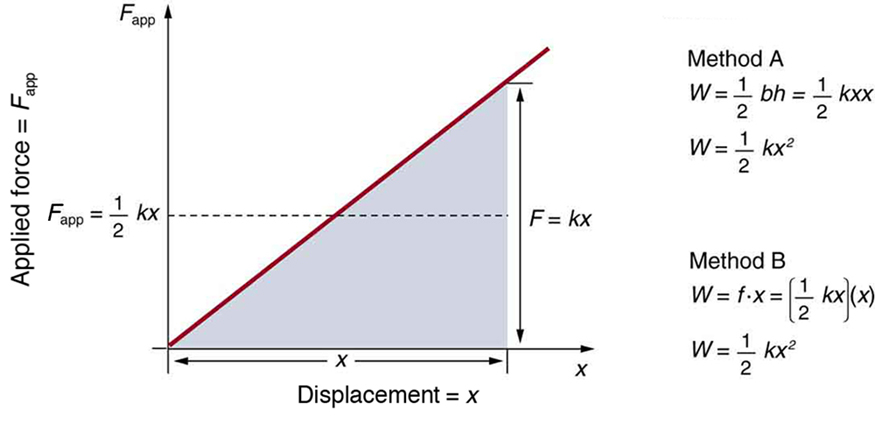
É possível encontrar o trabalho realizado na deformação de um sistema para encontrar a energia armazenada. Este trabalho é realizado por uma força aplicada\(F_{app}\). A força aplicada é exatamente oposta à força restauradora (ação-reação), e assim por diante\(F_{app} = kx\). \(\PageIndex{5}\)A figura mostra um gráfico da força aplicada versus deformação\(x\) em um sistema que pode ser descrito pela lei de Hooke. O trabalho realizado no sistema é a força multiplicada pela distância, que é igual à área sob a curva ou\(\dfrac{1}{2} kx^2\) (Método A na figura). Outra forma de determinar o trabalho é observar que a força aumenta linearmente de 0 para\(kx\), de modo que a força média é\((1/2)kx\), a distância percorrida é e\(x\), portanto,\(W = F_{app} d = [(1/2)kx](x) = (1/2)kx^2\) (Método B na figura).

O gráfico aqui representa a força aplicada, dada ao longo do eixo y, versus deformação ou deslocamento, dada ao longo do eixo x. A inclinação é inclinada linear e a área da inclinação é coberta entre o eixo x e a inclinação, dada por F é igual a k multiplicado por x, onde k é constante e x é deslocamento. A força aplicada ao longo do eixo y é dada pela metade de k multiplicada por x. Junto com o gráfico, dois métodos são fornecidos para calcular o peso, W. O primeiro método fornece a solução multiplicando metade de b multiplicado por h, enquanto no segundo podemos obter a solução multiplicando f por x. — Figura\(\PageIndex{5}\): Um gráfico da força aplicada versus distância para a deformação de um sistema que pode ser descrito pela lei de Hooke é exibido. O trabalho realizado no sistema é igual à área abaixo do gráfico ou à área do triângulo, que é metade de sua base multiplicada por sua altura, ou\(W = (1/2)kx^2\).

Exemplo\(\PageIndex{2}\): Calculating Stored Energy: A Tranquilizer Gun Spring

Podemos usar o mecanismo de mola de uma arma de brinquedo para fazer e responder a duas perguntas simples:

Quanta energia é armazenada na mola de uma pistola tranquilizante que tem uma força constante de 50,0 N/m e é comprimida 0,150 m?
Se você negligenciar o atrito e a massa da mola, a que velocidade um projétil de 2,00 g será ejetado da arma?

Figura\(\PageIndex{6}\): (a) Nesta imagem da arma, a mola é descomprimida antes de ser engatilhada. (b) A mola foi comprimida a uma distância\(x\) e o projétil está no lugar. (c) Quando liberada, a mola converte energia potencial elástica\(PR_{el}\) em energia cinética.

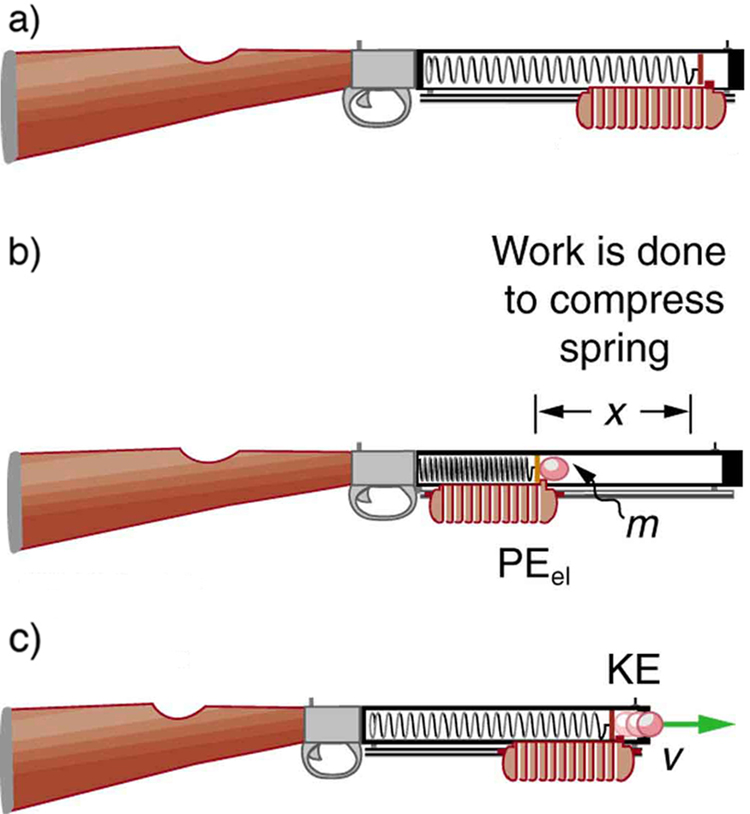
Estratégia para um

(a): A energia armazenada na primavera pode ser encontrada diretamente da equação da energia potencial elástica, porque\(k\) e\(x\) é dada.

Solução para um

Inserir os valores fornecidos para\(k\) e\(x\) rende

\[PE_{el} = \dfrac{1}{2}kx^2 = \dfrac{1}{2}(50.0 \, N/m)(0.150 \, m)^2 = 0.563 \, N \cdot m = 0.563 \, J\]

Estratégia para b

Como não há atrito, a energia potencial é totalmente convertida em energia cinética. A expressão da energia cinética pode ser resolvida pela velocidade do projétil.

Solução para b

Identifique quantidades conhecidas:

\[ KE_f = PE_{el} \, or \, 1/2 mv^2 = (1/2)kx^2 = PE_{el} = 0.563 \, J\]

2. Resolva para\(v\):

\[ v = \left[\dfrac{2PE_{el}}{m}\right] = \left[\dfrac{2(0.563 \, J)}{0.002 \, kg}\right] = 23.7(J/K)^{1/2}\]

3. Unidades de conversão:\(23.7 \, m/s\)

Discussão

(a) e (b): Essa velocidade de projétil é impressionante para um canhão tranquilizante (mais de 80 km/h). Os números desse problema parecem razoáveis. A força necessária para comprimir a mola é pequena o suficiente para um adulto gerenciar, e a energia transmitida ao dardo é pequena o suficiente para limitar os danos que ele pode causar. No entanto, a velocidade do dardo é grande o suficiente para percorrer uma distância aceitável.

Exercício\(\PageIndex{1}\): Check your Understanding

Imagine segurar a ponta de uma régua com uma mão e deformá-la com a outra. Ao soltar, você pode ver as oscilações da régua. De que forma você poderia modificar esse experimento simples para aumentar a rigidez do sistema?

Responda: Você pode segurar a régua em seu ponto médio para que a parte da régua que oscila tenha a metade do comprimento do experimento original.

Exercício\(\PageIndex{2}\): Check your Understanding

Se você aplicar uma força de deformação em um objeto e deixá-lo atingir o equilíbrio, o que aconteceu com o trabalho que você fez no sistema?

Responda: Foi armazenado no objeto como energia potencial.

Resumo

Uma oscilação é um movimento de ida e volta de um objeto entre dois pontos de deformação.
Uma oscilação pode criar uma onda, que é uma perturbação que se propaga de onde foi criada.
O tipo mais simples de oscilações e ondas está relacionado a sistemas que podem ser descritos pela lei de Hooke:\( F = -kx\) onde\(F\) está a força\(x\) restauradora,\(PE_{el}\) é o deslocamento do equilíbrio ou da deformação e\(PE_{el} = (1/2)kx^2.\)

Glossário

deformação: deslocamento do equilíbrio

energia potencial elástica: energia potencial armazenada como resultado da deformação de um objeto elástico, como o alongamento de uma mola

força constante: uma constante relacionada à rigidez de um sistema: quanto maior a constante de força, mais rígido é o sistema; a constante de força é representada por k

força restauradora: força agindo em oposição à força causada por uma deformação