10.6: Colisões de corpos estendidos em duas dimensões

Last updated
Save as PDF

Page ID: 194809

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Observe colisões de corpos estendidos em duas dimensões.
Examine a colisão no ponto de percussão.

Os pinos de boliche são lançados voando e girando quando atingidos por uma bola de boliche - momento angular, bem como impulso linear e energia foram transmitidos aos pinos. (Veja a Figura\(\PageIndex{1}\)). Muitas colisões envolvem momento angular. Os carros, por exemplo, podem girar e colidir no gelo ou em uma superfície molhada. Os arremessadores de beisebol lançam curvas girando na bola de beisebol. Um jogador de tênis pode dar muitas voltas na bola de tênis, o que faz com que ela mergulhe na quadra depois de cruzar a rede. Agora vamos dar uma breve olhada no que acontece quando objetos que podem girar colidem.

Uma bola de boliche, assim como está batendo nos pinos. — Figura\(\PageIndex{1}\): A bola de boliche faz com que os pinos voem, alguns deles girando violentamente. (crédito: Tinou Bao, Flickr)

Considere a colisão relativamente simples mostrada na Figura\(\PageIndex{2}\), na qual um disco bate e adere a um bastão inicialmente imóvel pregado em uma extremidade em uma superfície sem atrito. Após a colisão, os dois giram em torno do prego. Há uma força externa desequilibrada no sistema na unha. Essa força não exerce torque porque o braço da alavanca é zero. O momento angular é, portanto, conservado na colisão. A energia cinética não é conservada, porque a colisão é inelástica. É possível que o momento também não seja conservado porque a força no prego pode ter um componente na direção da velocidade inicial do disco. Vamos examinar um caso de rotação em uma colisão em Example\(\PageIndex{1}\).

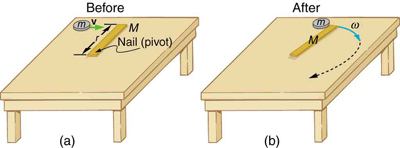
A Figura a mostra um disco m deslizando em direção a um bastão imóvel M de comprimento r girado em torno de um prego, em uma superfície sem atrito. Na figura b, um disco atinge o bastão em uma extremidade e adere a ele, e o bastão gira, girando ao redor do prego na direção mostrada pela seta no sentido horário e na velocidade angular ômega. — Figura\(\PageIndex{2}\): (a) Um disco desliza em direção a um bastão imóvel em uma superfície sem atrito. (b) O disco atinge o bastão em uma extremidade e adere a ele, e eles giram juntos, girando em torno do prego. O momento angular é conservado para essa colisão inelástica porque a superfície não tem atrito e a força externa desequilibrada no prego não exerce torque.

Exemplo\(\PageIndex{1}\): Rotation in a Collision

Suponha que o disco na Figura\(\PageIndex{2}\) tenha uma massa de 50,0 g e uma velocidade inicial de 30,0 m/s ao atingir o bastão de 1,20 m de comprimento e 2,00 kg.

Qual é a velocidade angular dos dois após a colisão?
Qual é a energia cinética antes e depois da colisão?
Qual é o momento linear total antes e depois da colisão?

Estratégia para (a)

Podemos responder à primeira pergunta usando a conservação do momento angular, conforme observado. Como o momento angular é\(I\omega\), podemos resolver a velocidade angular.

Solução para (a)

Conservação dos estados de momento angular

\[L = L',\]

onde quantidades primadas representam condições após a colisão e ambos os momentos são calculados em relação ao ponto de articulação. O momento angular inicial do sistema de disco rígido é o do disco imediatamente antes de atingir o manípulo. Ou seja,

\[L = I\omega,\]

onde\(I\) é o momento de inércia do disco e\(\omega\) sua velocidade angular em torno do ponto de articulação. Agora,\(I = mr^2\) (considerando que o disco tem aproximadamente uma massa pontual) e\(\omega = v/r\), de modo que

\[L = mr^2\dfrac{v}{r} = mvr.\]

Depois da colisão,

\[L' = I'\omega'.\]

É o\(\omega'\) que desejamos encontrar. A conservação do momento angular dá

\[I'\omega' = mvr.\]

Reorganizar a equação produz

\[\omega' = \dfrac{mvr}{I'},\]

onde\(I'\) está o momento de inércia do bastão e do disco presos juntos, que é a soma de seus momentos individuais de inércia sobre o prego. [link] fornece a fórmula para que uma haste girando em torno de uma extremidade seja\(I = Mr^2/3\). Assim,

\[I' = mr^2 + \dfrac{Mr^2}{3} = \left(m + \dfrac{M}{3}\right)r^2\]

Inserir valores conhecidos nessa equação produz,

\[I' = (0.0500 \, kg + 0.667 \, kg)(1.20 \, m)^2 = 1.032 \, kg \cdot m^2\]

O valor de agora\(I'\) é inserido na expressão for\(\omega'\), que gera

\[\omega' = \dfrac{mvr}{I'} = \dfrac{(0.0500 \, kg)(30.0 \, m/s)(1.20 \, m)}{1.032 \, kg \cdot m^2}\]

\[= 1.744 \, rad/s \approx 1.74 \, rad/s.\]

Estratégia para (b)

A energia cinética antes da colisão é a energia cinética translacional do disco de entrada e, após a colisão, é a energia cinética rotacional dos dois presos juntos.

Solução para (b)

Primeiro, calculamos a energia cinética translacional inserindo determinados valores para a massa e a velocidade do disco de entrada.

\[KE = \dfrac{1}{2}mv^2 = (0.500)(0.0500 \, kg)(30.0 \, m/s)^2 = 22.5 \, J.\]

Após a colisão, a energia cinética rotacional pode ser encontrada porque agora conhecemos a velocidade angular final e o momento final de inércia. Assim, inserir os valores na equação da energia cinética rotacional fornece

\[KE' = \dfrac{1}{2} I'\omega^{'2} = (0.5)(1.032 \, kg \cdot m^2)(1.744 \, rad/s)^2\]

\[= 1.57 \, J.\]

Estratégia para (c)

O momento linear antes da colisão é o do disco. Após a colisão, é a soma do momento do disco e do centro de massa do bastão.

Solução de (c)

Antes da colisão, então, o momento linear é

\[p = mv = (0.0500 \, kg)(30.0 \, m/s) = 1.50 \, kg \cdot m/s.\]

Após a colisão, o disco e o centro de massa do bastão se movem na mesma direção. O momento linear total é o do disco se movendo a uma nova velocidade\(v' = r\omega'\) mais a do centro de massa do bastão,

que se move na metade dessa velocidade porque\(v_{CM} = \left(\frac{r}{2}\right)\omega' = \frac{v'}{2}\). Assim,

\[p' = mv' + Mv_{CM} = mv' + \dfrac{Mv'}{2}.\]

A coleta de termos semelhantes na equação produz,

\[p' = \left(m + \dfrac{M}{2}\right)v'\]para que

\[p' = \left(m + \dfrac{M}{2}\right)r\omega'\]

Substituindo valores conhecidos na equação,

\[p' = (1.050 \, kg)(1.20 \, m)(1.744 \, rad/s) = 2.20 \, kg \cdot m/s.\]

Discussão

Primeiro, observe que a energia cinética é menor após a colisão, conforme previsto, porque a colisão é inelástica. O mais surpreendente é que o impulso após a colisão é realmente maior do que antes da colisão. Esse resultado pode ser entendido se você considerar como a unha afeta o bastão e vice-versa. Aparentemente, o bastão empurra o prego para trás quando é atingido pela primeira vez pelo disco. A reação do prego (consistente com a terceira lei de Newton) é empurrar o bastão para frente, transmitindo-lhe impulso na mesma direção em que o disco estava se movendo inicialmente, aumentando assim o impulso do sistema.

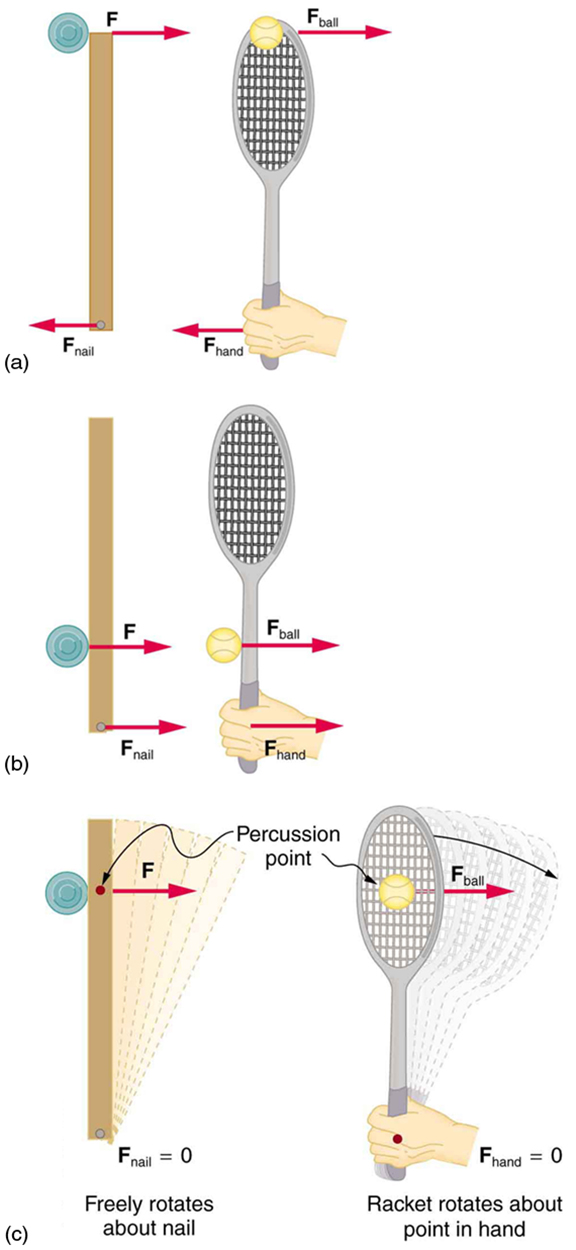
O exemplo acima tem outras implicações. Por exemplo, o que aconteceria se o disco batesse muito perto do prego? Obviamente, uma força seria exercida no prego na direção para frente. Assim, quando o bastão é atingido na extremidade mais distante do prego, uma força para trás é exercida sobre o prego e, quando ele é atingido na extremidade mais próxima do prego, uma força para frente é exercida sobre o prego. Assim, golpeá-lo em um determinado ponto intermediário não produz força na unha. Esse ponto intermediário é conhecido como ponto de percussão.

Uma situação análoga ocorre no tênis, conforme visto na Figura\(\PageIndex{3}\). Se você acertar uma bola com a ponta da raquete, a alça será afastada da sua mão. Se você acertar uma bola muito mais abaixo, por exemplo, no eixo da raquete, a alça é empurrada na palma da mão. E se você acertar a bola no ponto de percussão da raquete (o que algumas pessoas chamam de “ponto ideal”), pouca ou nenhuma força será exercida em sua mão e haverá menos vibração, reduzindo as chances de um cotovelo de tenista. O mesmo efeito ocorre com um taco de beisebol.

Na figura a, um disco batendo em um bastão é comparado a uma bola de tênis sendo atingida por uma raquete. Quando a bola atinge a raquete perto do final com uma força indicada pela bola f, conforme mostrado pela direção da flecha, uma força para trás, a mão f é exercida sobre a mão, Na figura b, quando a raquete é atingida muito mais para baixo por uma força F bola, uma força para frente, f mão é exercida na mão conforme mostrado pelas setas. Na figura (c), quando a raquete é atingida pela bola com uma força f no ponto de percussão, nenhuma força é aplicada à mão. Isso implica que a mão f é igual a zero. — Figura\(\PageIndex{3}\): Um disco batendo em um bastão é comparado a uma bola de tênis sendo atingida por uma raquete. (a) Quando a bola atinge a raquete perto do final, uma força para trás é exercida na mão. (b) Quando a raquete é atingida muito mais para baixo, uma força para frente é exercida na mão. (c) Quando a raquete é atingida no ponto de percussão, nenhuma força é aplicada à mão.

Exercício\(\PageIndex{1}\)

A energia cinética rotacional é um vetor? Justifique sua resposta.

Solução

Não, a energia é sempre escalar, independentemente de o movimento estar envolvido ou não. Nenhuma forma de energia tem uma direção no espaço e você pode ver que a energia cinética rotacional não depende da direção do movimento, assim como a energia cinética linear é independente da direção do movimento.

Resumo

O momento angular\(L\) é análogo ao momento linear e é dado por\(L = I\omega\).
O momento angular é alterado pelo torque, seguindo a relação\(net \, \tau = \frac{\Delta L}{\Delta t}\).
O momento angular é conservado se o torque líquido for zero\(L = constant \, (net \, \tau = 0)\) ou\(L = L' \, (net \, \tau = 0)\). Essa equação é conhecida como a lei da conservação do momento angular, que pode ser conservada em colisões.