Skip to main content
Global

8.2: Impulso

  1. Last updated
  2. Save as PDF
  • Page ID
    194258

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Defina impulso.
    • Descreva os efeitos dos impulsos na vida cotidiana.
    • Determine a força efetiva média usando representação gráfica.
    • Calcule a força e o impulso médios com base na massa, velocidade e tempo.

    O efeito de uma força em um objeto depende de quanto tempo ele age, bem como de quão grande é a força. Em [link], uma força muito grande atuando por um curto período teve um grande efeito no ímpeto da bola de tênis. Uma força pequena poderia causar a mesma mudança de impulso, mas teria que agir por muito mais tempo. Por exemplo, se a bola fosse lançada para cima, a força gravitacional (que é muito menor do que a força da raquete de tênis) acabaria por reverter o impulso da bola. Quantitativamente, o efeito de que estamos falando é a mudança no momentum\(\Delta p\).

    Ao reorganizar a equação\(\Delta F_{net} = \frac{\Delta p}{\Delta t} \) para ser

    \[\Delta p = F_{net} \Delta t,\]

    podemos ver como a mudança no momentum é igual à força externa líquida média multiplicada pelo tempo em que essa força atua. A quantidade\(F_{net} \Delta t\) recebe o nome de impulso. O impulso é o mesmo que a mudança no momentum.

    Impulso: Mudança no momentum

    A mudança no momentum é igual à força externa líquida média multiplicada pelo tempo em que essa força atua.

    \[\Delta p = F_{net} \Delta t\]

    A quantidade\( F_{net}\Delta t\) recebe o nome de impulso.

    Há muitas maneiras pelas quais uma compreensão do impulso pode salvar vidas, ou pelo menos membros. O acolchoamento do painel de um carro e, certamente, os airbags, permitem que a força líquida sobre os ocupantes do carro atue por muito mais tempo quando há uma parada repentina. A mudança de momentum é a mesma para um ocupante, independentemente de um airbag estar instalado ou não, mas a força (para parar o ocupante) será muito menor se ele agir por um período maior. Hoje, os carros têm muitos componentes de plástico. Uma vantagem dos plásticos é seu menor peso, o que resulta em melhor consumo de combustível. Outra vantagem é que um carro se deforma em uma colisão, especialmente no caso de uma colisão frontal. Um tempo de colisão mais longo significa que a força no carro será menor. As mortes durante corridas de carros diminuíram drasticamente quando as estruturas rígidas dos carros de corrida foram substituídas por peças que poderiam se deformar ou desmoronar em caso de acidente.

    Os ossos de um corpo se fraturarão se a força sobre eles for muito grande. Se você pular de uma mesa no chão, a força em suas pernas pode ser imensa se você pousar com as pernas rígidas em uma superfície dura. Rolar no chão depois de pular da mesa ou pousar com um paraquedas prolonga o tempo durante o qual a força (sobre você do chão) atua.

    Exemplo\(\PageIndex{1}\): Calculating Magnitudes of Impulses: Two Billiard Balls Striking a Rigid Wall

    Duas bolas de bilhar idênticas atingem uma parede rígida com a mesma velocidade e são refletidas sem qualquer alteração de velocidade. A primeira bola bate perpendicularmente à parede. A segunda bola atinge a parede em um ângulo\(30^o\) de relação à perpendicular e ricocheteia em um ângulo\(30^o\) perpendicular à parede.

    1. Determine a direção da força na parede devido a cada bola.
    2. Calcule a proporção das magnitudes dos impulsos nas duas bolas ao lado da parede.

    Estratégia para (a)

    Para determinar a força na parede, considere a força na bola devido à parede usando a segunda lei de Newton e, em seguida, aplique a terceira lei de Newton para determinar a direção. Suponha que o\(x-\) eixo esteja normal em relação à parede e seja positivo na direção inicial do movimento. Escolha o\(y-\) eixo a ser colocado ao longo da parede no plano do movimento da segunda bola. A direção do momento e a direção da velocidade são as mesmas.

    Estratégia para (a)

    Para determinar a força na parede, considere a força na bola devido à parede usando a segunda lei de Newton e, em seguida, aplique a terceira lei de Newton para determinar a direção. Suponha que o\(x-\) eixo esteja normal em relação à parede e seja positivo na direção inicial do movimento. Escolha o\(y-\) eixo a ser colocado ao longo da parede no plano do movimento da segunda bola. A direção do momento e a direção da velocidade são as mesmas.

    Solução para (a)

    A primeira bola salta diretamente na parede e exerce uma força sobre ela na\(x\) direção +. Portanto, a parede exerce uma força sobre a bola na\(y\) direção -. A segunda bola continua com o mesmo componente de momento na\(y-\) direção, mas inverte seu\(x\) componente de momento, como visto esboçando um diagrama dos ângulos envolvidos e tendo em mente a proporcionalidade entre velocidade e momento.

    Essas mudanças significam que a mudança no impulso de ambas as bolas está na\(-x\) direção, então a força da parede em cada bola está ao longo da\(-x\) direção.

    Estratégia para (b)

    Calcule a mudança no momento de cada bola, que é igual ao impulso transmitido à bola.

    Solução para (b)

    \(\mu\)Seja a velocidade de cada bola antes e depois da colisão com a parede e\(m\) a massa de cada bola. Escolha o\(x-\)\(y-\) eixo e o eixo conforme descrito anteriormente e considere a mudança no momento da primeira bola que atinge perpendicularmente à parede.

    \[p_{xi} = m\mu; \, p_{yi} = 0\]

    \[p_{xf} = -m\mu; \, p_{yf} = 0\]

    Impulso é a mudança no vetor de momentum. Portanto, o\(x-\) componente do impulso é igual a -\(2m\mu\) e o\(y-\) componente do impulso é igual a zero.

    Agora, considere a mudança no momentum da segunda bola.

    \[p_{xi} = m/mu \, cos 30^o; \, p_{yi} = -m\mu \, 30^o\]

    \[p_{xf} = -m/mu \, cos 30^o; \, p_{yf} = -m\mu \, 30^o\]

    Deve-se notar aqui que, embora\(p_x\) as mudanças sinalizem após a colisão,\(p_y\) não. Portanto, o componente -do impulso é igual a\(-2m\mu \, cos \, 30^o\) e o\(y-\) componente do impulso é igual a zero.

    A proporção das magnitudes do impulso transmitido às bolas é

    \[ \dfrac{2m\mu}{2m\mu \, 30^o} = \dfrac{2}{sqrt{3}} = 1.155.\]

    Discussão

    A direção do impulso e da força é a mesma do caso de (a); é normal para a parede e ao longo da\(x-\) direção negativa. Fazendo uso da terceira lei de Newton, a força na parede devido a cada bola é normal na parede na\(x-\) direção positiva.

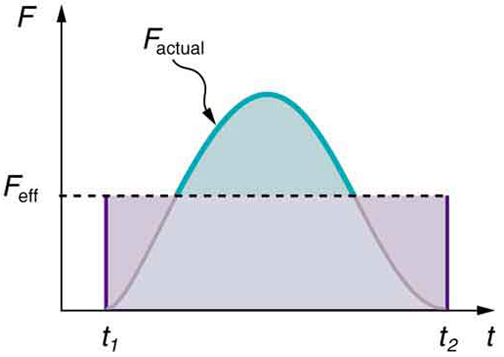
    Nossa definição de impulso inclui a suposição de que a força é constante ao longo do intervalo de tempo\(\Delta t\). As forças geralmente não são constantes. As forças variam consideravelmente mesmo durante os breves intervalos de tempo considerados. No entanto, é possível encontrar uma força efetiva média\(F_{eff}\) que produza o mesmo resultado que a força variável no tempo correspondente. A figura mostra um gráfico da aparência de uma força real em função do tempo de uma bola quicando no chão. A área abaixo da curva tem unidades de momento e é igual ao impulso ou mudança no momento entre os tempos\(t_1\)\(t_2\) e. Essa área é igual à área dentro do retângulo delimitada por\(F_{eff}, \, t_1\), e,\(t_2\) portanto, os impulsos e seus efeitos são os mesmos para as forças reais e efetivas.

    A figura é um gráfico da força, F, versus tempo, t. Duas curvas, F real e F efetiva, são desenhadas. F real é desenhado entre t sub1 e t sub 2 e se assemelha a uma curva em forma de sino que atinge o pico a meio caminho entre t sub 1 e t sub 2. F efetivo é uma linha paralela ao eixo x desenhada a cerca de cinquenta e cinco por cento do valor máximo de F real e se estende até t sub 2.
    Figura\(\PageIndex{1}\): Um gráfico de força versus tempo com tempo ao longo do\(x-\) eixo e força ao longo do\(y-\) eixo para uma força real e uma força efetiva equivalente. As áreas abaixo das duas curvas são iguais.

    FAZENDO CONEXÕES: Investigação para levar para casa — movimento e impulso das mãos

    Tente pegar uma bola enquanto “dá” com a bola, puxando as mãos em direção ao corpo. Em seguida, tente pegar uma bola enquanto mantém as mãos paradas. Bata água em uma banheira com a palma da mão cheia. Depois que a água baixar, bata na água novamente mergulhando a mão com os dedos primeiro na água. (Sua palma inteira representa um nadador fazendo um flop de barriga e sua mão mergulhadora representa um nadador fazendo um mergulho.) Explique o que acontece em cada caso e por quê. Quais orientações você aconselharia as pessoas a evitar e por quê?

    FAZENDO CONEXÕES: Força constante e aceleração constantes

    A suposição de uma força constante na definição de impulso é análoga à suposição de uma aceleração constante na cinemática. Em ambos os casos, a natureza é adequadamente descrita sem o uso do cálculo.

    Resumo

    • Impulso, ou mudança no momento, é igual à força externa líquida média multiplicada pelo momento em que essa força atua:

    \[ \Delta p = F_{net}\Delta t.\]

    • As forças geralmente não são constantes durante um período de tempo.

    Glossário

    mudança no momentum
    a diferença entre o momento final e o inicial; a massa vezes a mudança na velocidade
    impulso
    a força externa líquida média vezes o tempo em que ela age; igual à mudança no momento