4.7: Outras aplicações das Leis do Movimento de Newton

Last updated
Save as PDF

Page ID: 194799

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Aplique técnicas de resolução de problemas para resolver quantidades em sistemas de forças mais complexos.
Integre conceitos da cinemática para resolver problemas usando as leis do movimento de Newton.

Há muitas aplicações interessantes das leis do movimento de Newton, algumas das quais são apresentadas nesta seção. Eles também servem para ilustrar algumas outras sutilezas da física e para ajudar a desenvolver habilidades de resolução de problemas.

Exemplo\(\PageIndex{1}\): Drag Force on a Barge

Suponha que dois rebocadores empurrem uma barcaça em ângulos diferentes, conforme mostrado na Figura. O primeiro rebocador exerce uma força\(2.7 \times 10^5 \, N \) na direção x, e o segundo rebocador exerce uma força\(3.6 \times 10^5 \, N \) na direção y.

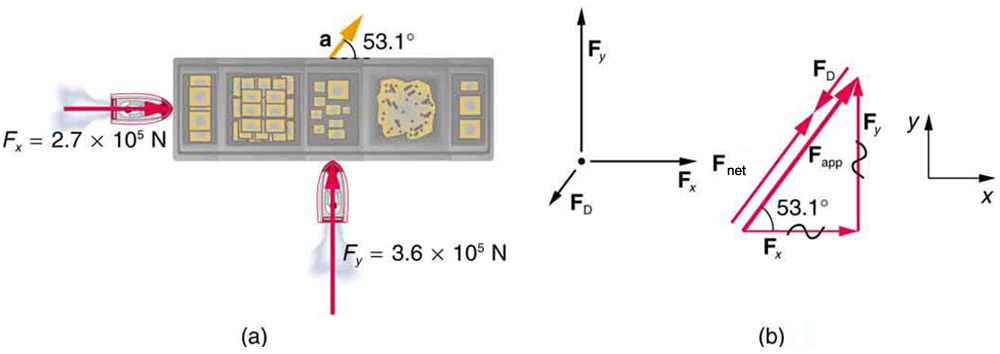
(a) Uma vista de cima de dois rebocadores empurrando uma barcaça. Um rebocador está empurrando com a força F sub x igual a dois pontos sete multiplicada por dez elevada a cinco newtons, mostrada por uma seta vetorial atuando para a direita na direção x. Outro rebocador está empurrando com uma força F sub y igual a três ponto seis multiplicada por dez elevado a cinco newtons atuando para cima na direção y positiva. A aceleração da barcaça, a, é mostrada por uma seta vetorial direcionada a cinquenta e três pontos de um ângulo de um grau acima do eixo x. No diagrama de corpo livre, F sub y está agindo em um ponto para cima, F sub x está agindo para a direita e F sub D está atuando aproximadamente a sudoeste. (b) Um triângulo reto é formado pelos vetores F sub x e F sub y. O vetor base é mostrado pelo vetor de força F sub x. e o vetor perpendicular é mostrado pelo vetor de força F sub y. O resultado é a hipotenusa desse triângulo, formando um ângulo de cinquenta e três pontos a um grau da base, mostrado pelo vetor força F subrede apontando para cima na inclinação. Um vetor F sub D aponta para baixo na inclinação. — Figura\(\PageIndex{1}\): (a) Vista de cima de dois rebocadores empurrando uma barcaça. (b) O diagrama de corpo livre do navio contém apenas forças atuando no plano da água. Ele omite as duas forças verticais: o peso da barcaça e a força de empuxo da água que a sustenta, cancelam e não são mostrados. Como as forças aplicadas são perpendiculares, os eixos x e y estão na mesma direção de\(F_x\) e.\(F_y\) O problema rapidamente se torna um problema unidimensional na direção de\(F_{app} \), já que o atrito está na direção oposta a.\(F_{app} \)

Se a massa da barcaça é\(5.0 \times 10^6 \space kg \) e sua aceleração é observada\(7.5 \times 10^{-2} \, m/s^2 \) na direção mostrada, qual é a força de arrasto da água na barcaça resistindo ao movimento? (Nota: a força de arrasto é uma força de atrito exercida por fluidos, como ar ou água. A força de arrasto se opõe ao movimento do objeto.)

Estratégia

As direções e magnitudes da aceleração e as forças aplicadas são dadas na Figura (a). Definiremos a força total dos rebocadores na barcaça de\(F_{app} \) forma que:\[ F_{app} = F_x + F_y \nonumber \]

Como a barcaça tem fundo plano, o arrasto da água\(F_D\) estará na direção oposta à\(F_{app} \) mostrada no diagrama de corpo livre na Figura (b). O sistema de interesse aqui é a barcaça, já que as forças nela são dadas, assim como sua aceleração. Nossa estratégia é encontrar a magnitude e a direção da força líquida aplicada e\(F_{app} \), em seguida, aplicar a segunda lei de Newton para resolver a força de arrasto\(F_D\).

Solução

Como\(F_x\) e\(F_y\) são perpendiculares, a magnitude e a direção de\(F_{app}\) são facilmente encontradas. Primeiro, a magnitude resultante é dada pelo teorema de Pitágoras:

\[F_{app} = \sqrt{F_x^2 + F_y^2} \nonumber \]

\[F_{app} = \sqrt{(2.7 \times 10^5 \, N)^2 + (3.6 \times 10^5 \, N)^2} = 4.5 \times 10^5 \, N. \nonumber \]

O ângulo é dado por\[ \theta = tan^{-1} \left(\dfrac{F_y}{F_x} \right) \nonumber \]

\[ \theta = tan^{-1} \left( \dfrac{3.6 \times 10^5 \, N}{2.7 \times 10^5 \, N} \right) = 53^o, \nonumber \]

que sabemos, por causa da primeira lei de Newton, é a mesma direção da aceleração. \(F_D\)está na direção oposta de\(F_{app} \), pois age para diminuir a aceleração. Portanto, a força externa líquida está na mesma direção que\(F_{app} \), mas sua magnitude é um pouco menor que\(F_{app} \). O problema agora é unidimensional. Na Figura (b), podemos ver que

\[F_{net} = F_{app} - F_D. \nonumber \]Mas a segunda lei de Newton afirma que\[ F_{net} = ma \nonumber \]

Assim,\[ F_{app} - F_D = ma \nonumber \]

Isso pode ser resolvido pela magnitude da força de arrasto da água\(F_D\) em termos de quantidades conhecidas:\[ F_D = F_{app} - ma \nonumber \] Substituir valores conhecidos fornece\[ F_D = (4.5 \times 10^5 \, N) - (5.0 \times 10^6 \, kg)(7.5 \times 10^{-2} \, m/s^2) = 7.5 \times 10^4 \, N \nonumber \]

A direção de\(F_D\) já foi determinada como sendo na direção oposta\(F_{app} \) ou em um ângulo de\(53^o\) sul ou oeste.

Discussão

Os números usados neste exemplo são razoáveis para uma barcaça moderadamente grande. Certamente é difícil obter acelerações maiores com rebocadores, e pequenas velocidades são desejáveis para evitar que a barcaça caia entre as docas. O arrasto é relativamente pequeno para um casco bem projetado em baixas velocidades, consistente com a resposta a este exemplo, onde\(F_D\) é menos de 1/600 do peso do navio.

No exemplo anterior de um equilibrista, observamos que as tensões nos fios que sustentavam uma massa eram iguais apenas porque os ângulos de cada lado eram iguais. Considere o exemplo a seguir, em que os ângulos não são iguais; um pouco mais de trigonometria está envolvida.

Exemplo\(\PageIndex{2}\): Different Tensions at Different Angles

Considere o semáforo (massa 15,0 kg) suspenso por dois fios, conforme mostrado na Figura. Encontre a tensão em cada fio, negligenciando as massas dos fios.

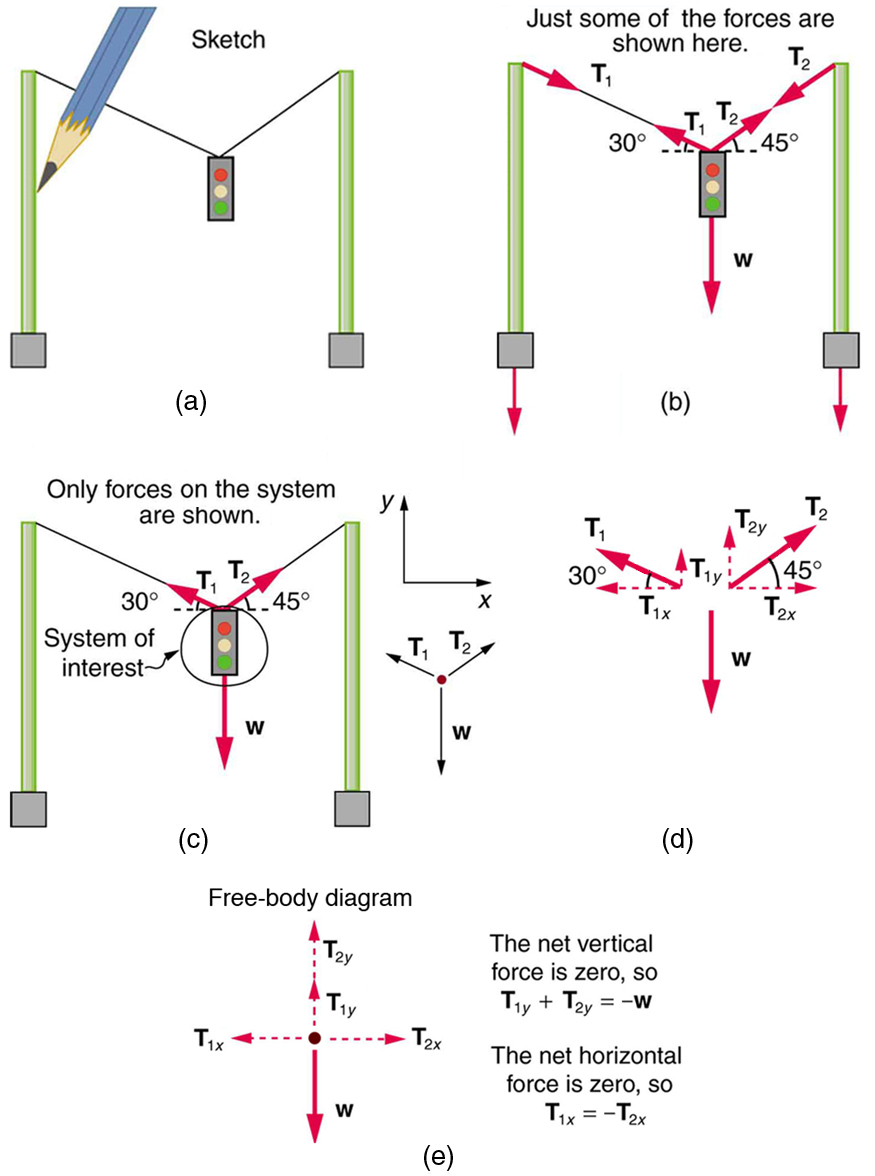
É mostrado um esboço de um semáforo suspenso por dois fios suportados por dois postes. (b) Algumas forças são mostradas neste sistema. A tensão T sub um puxando a parte superior do poste esquerdo é mostrada pela seta vetorial ao longo do fio esquerdo a partir do topo do poste, e uma tensão T sub um igual, mas oposta, é mostrada pela seta apontando para cima ao longo do fio esquerdo, onde está conectado à luz; o fio faz um ângulo de trinta graus com o horizontal. A tensão T sub dois é mostrada por uma seta vetorial apontando para baixo a partir da parte superior do poste direito ao longo do fio direito, e uma tensão igual, mas oposta, T sub dois, é mostrada pela seta apontando para cima ao longo do fio direito, que forma um ângulo de quarenta e cinco graus com a horizontal. O semáforo está suspenso na extremidade inferior dos fios e seu peso W é mostrado por uma seta vetorial atuando para baixo. (c) O semáforo é o sistema de interesse. A tensão T subum a partir do semáforo é mostrada por uma seta ao longo do fio fazendo um ângulo de trinta graus com a horizontal. A tensão T sub dois a partir do semáforo é mostrada por uma seta ao longo do fio fazendo um ângulo de quarenta e cinco graus com a horizontal. O peso W é mostrado por uma seta vetorial apontando para baixo a partir do semáforo. Um diagrama de corpo livre é mostrado com três forças atuando em um ponto. O peso W atua para baixo; T sub um e T sub dois agem em um ângulo com a vertical. (d) As forças são mostradas com seus componentes T sub um y e T sub dois y apontando verticalmente para cima. T sub um x pontos ao longo da direção x negativa, T sub dois pontos x ao longo da direção x positiva e peso W pontos verticalmente para baixo. (e) As forças verticais e as forças horizontais são mostradas separadamente. As forças verticais T sub um y e T sub dois y são mostradas por setas vetoriais atuando ao longo de uma linha vertical apontando para cima, e o peso W é mostrado por uma seta vetorial atuando para baixo. A força vertical líquida é zero, então T sub um y mais T sub dois y é igual a W. Por outro lado, T sub dois x é mostrado por uma seta apontando para a direita e T sub um x é mostrado por uma seta apontando para a esquerda. A força horizontal líquida é zero, então T sub um x é igual a T sub dois x. — Figura\(\PageIndex{2}\): Um semáforo está suspenso por dois fios. (b) Algumas das forças envolvidas. (c) Somente as forças que atuam no sistema são mostradas aqui. O diagrama de corpo livre do semáforo também é mostrado. (d) As forças projetadas nos eixos vertical (y) e horizontal (x). Os componentes horizontais das tensões devem ser cancelados e a soma dos componentes verticais das tensões deve ser igual ao peso do semáforo. (e) O diagrama de corpo livre mostra as forças verticais e horizontais atuando no semáforo.

Estratégia

O sistema de interesse é o semáforo, e seu diagrama de corpo livre é mostrado na Figura (c). As três forças envolvidas não são paralelas e, portanto, devem ser projetadas em um sistema de coordenadas. O sistema de coordenadas mais conveniente tem um eixo vertical e um horizontal, e as projeções vetoriais nele são mostradas na parte (d) da figura. Há duas incógnitas neste problema (\(T_1\)e T_2\)), então duas equações são necessárias para encontrá-las. Essas duas equações vêm da aplicação da segunda lei de Newton ao longo dos eixos vertical e horizontal, observando que a força externa líquida é zero ao longo de cada eixo porque a aceleração é zero.

Solução

Primeiro, considere o eixo horizontal ou o eixo x:\[F_{net \, x} = T_{2x} - T_{1x} = 0. \nonumber \]

Assim, como você poderia esperar,\[T_{1x} = T{2x} \nonumber \]

Isso nos dá a seguinte relação entre\(T_1\) e\(T_2\):\[T_1 \, cos \, 30^o = T_2 \, cos\space 45^o \nonumber \]

Assim,\[ T_2 = (1.225)T_1. \nonumber \]

Observe que\( T_1 \) e não\(T_2\) são iguais nesse caso, porque os ângulos em ambos os lados não são iguais. É razoável que\(T_2\) acabe sendo maior do que\(T_1\), porque é exercido mais verticalmente do que\(T_1\).

Agora, considere os componentes de força ao longo do eixo vertical ou y:

\[ F_{net \, y} = T_{1y} +T_{2y} - w= 0 \nonumber \]

Isso implica\[ T_{1y} +T_{2y} = w \nonumber \]

Substituir as expressões pelos componentes verticais dá\[ T_1 \, sin \, (30^o) + T_2 \, sin \, (45^o) = w. \nonumber \]

Existem duas incógnitas nessa equação, mas substituir a expressão por\(T_2\) em termos de\(T_1\) reduz isso a uma equação por uma desconhecida:

\[T_1(0.500) + (1.225T_1)(0.707) = w = mg \nonumber \]

que rende\[ (1.366)T_1 = (15.0 \, kg)(9.80 \, m/s^2). \nonumber \]

Resolver esta última equação dá a magnitude\(T_1\) de ser\[ T_1 = 108 \, N. \nonumber \]

Finalmente, a magnitude de\(T_2\) é determinada usando a relação entre eles,\(T_2= 1.225 T_1 \) encontrada acima. Assim, obtemos

\[ T_2 = 132 \, N. \nonumber \]

Discussão

Ambas as tensões seriam maiores se os dois fios fossem mais horizontais e seriam iguais se e somente se os ângulos de cada lado fossem os mesmos (como eram no exemplo anterior de um andador de corda bamba).

A balança de banheiro é um excelente exemplo de uma força normal atuando em um corpo. Ele fornece uma leitura quantitativa de quanto ele deve empurrar para cima para suportar o peso de um objeto. Mas você consegue prever o que veria no mostrador de uma balança de banheiro se estivesse sobre ela durante uma viagem de elevador? Você verá um valor maior do que seu peso quando o elevador for ligado? E quando o elevador se move para cima a uma velocidade constante: a balança ainda lerá mais do que seu peso em repouso? Considere o exemplo a seguir.

Exemplo\(\PageIndex{3}\): What does the Bathroom Scale Read in an Elevator?

A figura mostra um homem de 75,0 kg (peso de cerca de 165 libras) parado em uma balança de banheiro em um elevador. Calcule a leitura da escala: (a) se o elevador acelerar para cima a uma taxa de\(1.20 m/s^2 \) e (b) se o elevador se mover para cima a uma velocidade constante de 1 m/s.

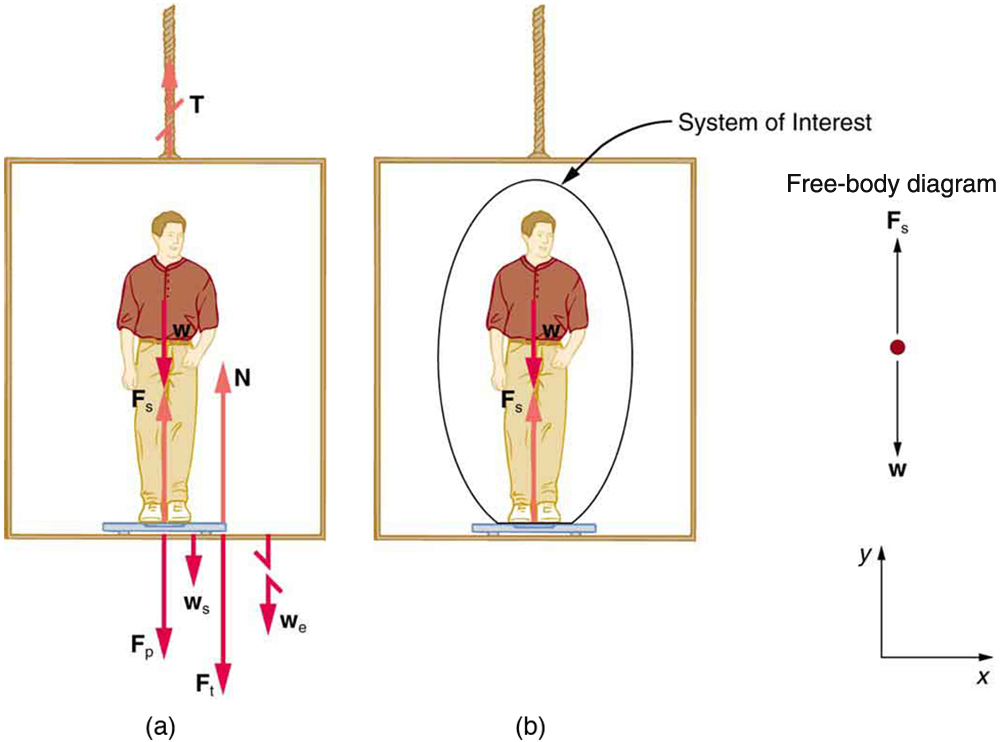
Uma pessoa está parada em uma balança de banheiro em um elevador. Seu peso w é mostrado por uma seta apontando para baixo. F sub s é a força da balança sobre a pessoa, mostrada por um vetor partindo de seus pés apontando verticalmente para cima. W sub s é o peso da balança apontando verticalmente para baixo. W sub e é o peso do elevador, mostrado pela seta quebrada apontando verticalmente para baixo. F sub p é a força da pessoa na balança, atuando verticalmente para baixo. F sub t é a força da balança no piso do elevador, apontando verticalmente para baixo, e N é a força normal do piso na balança, apontando para cima. (b) A mesma pessoa é mostrada na balança do elevador, mas apenas algumas forças são mostradas atuando sobre a pessoa, que é o nosso sistema de interesse. W é mostrado por uma seta atuando para baixo, e F sub s é a força da escala na pessoa, mostrada por um vetor que começa com seus pés apontando verticalmente para cima. O diagrama de corpo livre também é mostrado, com duas forças atuando em um ponto. F sub s atua verticalmente para cima e w atua verticalmente para baixo. — Figura\(\PageIndex{3}\) :( a) As várias forças que atuam quando uma pessoa está em uma balança de banheiro em um elevador. As setas estão aproximadamente corretas para quando o elevador está acelerando para cima — flechas quebradas representam forças muito grandes para serem desenhadas em escala. \(T\)é a tensão no cabo de suporte,\(w\) é o peso da pessoa,\(w_s\) é o peso da balança,\(w_e\) é o peso do elevador,\(F_s\) é a força da balança na pessoa,\(F_p\) é a força da pessoa na balança,\(F_t\) é a força do escala no chão do elevador, e\(N\) é a força do piso para cima na balança. (b) O diagrama de corpo livre mostra apenas as forças externas que atuam no sistema de interesse designado — a pessoa.

Estratégia

Se a escala for precisa, sua leitura será igual\(F_p\) à magnitude da força que a pessoa exerce sobre ela. A Figura (a) mostra as inúmeras forças que atuam no elevador, na balança e na pessoa. Isso faz com que esse problema unidimensional pareça muito mais formidável do que se a pessoa fosse escolhida para ser o sistema de interesse e um diagrama de corpo livre fosse desenhado como na Figura (b). A análise do diagrama de corpo livre usando as leis de Newton pode produzir respostas para as partes (a) e (b) desse exemplo, bem como para algumas outras questões que possam surgir. As únicas forças que atuam sobre a pessoa são seu peso\(w\) e a força ascendente da balança.\(F_s.\) De acordo com a terceira lei\(F_p\) de Newton,\(F_s\) são iguais em magnitude e direção oposta, então precisamos encontrar\(F_s\) para encontrar o que a balança diz. Podemos fazer isso, como sempre, aplicando a segunda lei de Newton,

\[F_{net} = ma \nonumber \]

A partir do diagrama de corpo livre, vemos\(F_{net} = F_s - w, \) isso para que\[ F_s - w = ma. \nonumber \]

Resolver para\(F_s\) dá uma equação com apenas uma incógnita:\[ F_s = ma + w, \nonumber \]

ou, porque\(w = mg \), simplesmente\[ F_s = ma + mg. \nonumber \]

Nenhuma suposição foi feita sobre a aceleração e, portanto, essa solução deve ser válida para uma variedade de acelerações, além das deste exercício.

Solução para (a)

Nesta parte do problema,\(a = 1.20 m/s^2\), de modo que

\[ F_s = (75.0 \, kg)(1.20 \, m/s^2) + (75.0 \, kg)(9.80 \, m/s^2), \nonumber \]

produzindo\[ F_s = 825 \, N. \nonumber \]

Discussão para (a)

Isso é cerca de 185 libras. O que a balança teria lido se ele estivesse parado? Como sua aceleração seria zero, a força da balança seria igual ao seu peso:

\[ F_{net} = ma = 0 = F_s - w\nonumber \]

\[ F_s = w = mg \nonumber \]

\[F_s = (75.0 \, kg)(9.80 \, m/s^2) \nonumber \]

\[F_s = 735 \, N. \nonumber \]

Portanto, a leitura da balança no elevador é maior do que seu peso de 735 N (165 lb). Isso significa que a balança está empurrando a pessoa com uma força maior que seu peso, como deveria, para acelerá-la para cima. Claramente, quanto maior a aceleração do elevador, maior a leitura da escala, consistente com o que você sente em elevadores acelerando rapidamente versus acelerando lentamente.

Solução para (b)

Agora, o que acontece quando o elevador atinge uma velocidade ascendente constante? A balança ainda lerá mais do que seu peso? Para qualquer velocidade constante — para cima, para baixo ou estacionária — a aceleração é zero porque\(a = \frac{\Delta v}{\Delta t} \)\(\Delta v = 0 \) e.

Assim,\[F_s = ma + mg = 0 + mg. \nonumber \]

Agora\[ F_s = (75.0 \, kg)(9.80 \, m/s^2), \nonumber \]

que dá\[ F_s = 735 \, N. \nonumber \]

Discussão para (b)

A leitura da balança é 735 N, o que equivale ao peso da pessoa. Esse será o caso sempre que o elevador tiver uma velocidade constante — subindo, descendo ou parado.

A solução para o exemplo anterior também se aplica a um elevador acelerando para baixo, conforme mencionado. Quando um elevador acelera para baixo,\(a\) é negativo e a leitura da balança é menor que o peso da pessoa, até que uma velocidade descendente constante seja atingida, momento em que a leitura da balança novamente se torna igual ao peso da pessoa. Se o elevador estiver em queda livre e acelerando para baixo\(g\), a leitura da balança será zero e a pessoa parecerá estar sem peso.

Integrando conceitos: as leis do movimento e da cinemática de Newton

A física é mais interessante e poderosa quando aplicada a situações gerais que envolvem mais do que um conjunto restrito de princípios físicos. As leis do movimento de Newton também podem ser integradas a outros conceitos que foram discutidos anteriormente neste texto para resolver problemas de movimento. Por exemplo, forças produzem acelerações, um tópico de cinemática e, portanto, a relevância dos capítulos anteriores. Ao abordar problemas que envolvem vários tipos de forças, aceleração, velocidade e/ou posição, use as seguintes etapas para abordar o problema:

Estratégia de resolução de problemas

Etapa 1. Identifique quais princípios físicos estão envolvidos. Listar os dados fornecidos e as quantidades a serem calculadas permitirá que você identifique os princípios envolvidos.

Etapa 2. Resolva o problema usando as estratégias descritas no texto. Se eles estiverem disponíveis para o tópico específico, você deve consultá-los. Você também deve consultar as seções do texto que tratam de um tópico específico. O exemplo prático a seguir ilustra como essas estratégias são aplicadas a um problema de conceito integrado.

Exemplo\(\PageIndex{4}\): What Force Must a Soccer Player Exert to Reach Top Speed?

Um jogador de futebol começa do repouso e acelera para frente, atingindo uma velocidade de 8,00 m/s em 2,50 s. (a) Qual foi sua aceleração média? (b) Que força média ele exerceu para trás no solo para alcançar essa aceleração? A massa do jogador é de 70,0 kg e a resistência do ar é insignificante.

Estratégia

Para resolver um problema de conceito integrado, devemos primeiro identificar os princípios físicos envolvidos e identificar os capítulos nos quais eles se encontram. A parte (a) deste exemplo considera a aceleração ao longo de uma linha reta. Esse é um tópico de cinemática. A parte (b) trata da força, um tópico de dinâmica encontrado neste capítulo.
As soluções a seguir para cada parte do exemplo ilustram como as estratégias específicas de solução de problemas são aplicadas. Isso envolve identificar conhecidos e incógnitos, verificar se a resposta é razoável e assim por diante.

Solução para (a)

Recebemos as velocidades inicial e final (zero e 8,00 m/s para frente); portanto, a mudança na velocidade é\(\Delta v = 8.00 \, m/s \). Nós recebemos o tempo decorrido, e assim por diante\(\Delta t = 2.50 \, s\). O desconhecido é a aceleração, que pode ser encontrada em sua definição:

\[ a = \dfrac{\Delta v}{\Delta t}. \nonumber \]

Substituir os valores conhecidos produz\[ a = \dfrac{8.00 \, m/s}{2.50 \, s} = 3.20 \, m/s^2 \nonumber \]

Discussão para (a)

Esta é uma aceleração alcançável para um atleta em boas condições.

Solução para (b)

Aqui, somos solicitados a encontrar a força média que o jogador exerce para trás para alcançar essa aceleração para frente. Negligenciando a resistência do ar, isso seria igual em magnitude à força externa líquida sobre o jogador, pois essa força causa sua aceleração. Como agora conhecemos a aceleração do jogador e recebemos sua massa, podemos usar a segunda lei de Newton para encontrar a força exercida. Ou seja,

\[ F_{net} = ma\nonumber \]

Substituindo os valores conhecidos de\(m\) e\(a\) dá

\[ F_{net} = (70 \, kg)(3.2 \, m/s^2) = 224 \, N. \nonumber \]

Discussão para (b)

Isso é cerca de 50 libras, uma força média razoável.

Este exemplo prático ilustra como aplicar estratégias de resolução de problemas a situações que incluem tópicos de diferentes capítulos. O primeiro passo é identificar os princípios físicos envolvidos no problema. O segundo passo é resolver o desconhecido usando estratégias familiares de resolução de problemas. Essas estratégias são encontradas em todo o texto, e muitos exemplos úteis mostram como usá-las para tópicos individuais. Você encontrará essas técnicas para problemas de conceito integrados úteis em aplicações da física fora de um curso de física, como em sua profissão, em outras disciplinas científicas e na vida cotidiana. Os problemas a seguir desenvolverão suas habilidades na ampla aplicação dos princípios físicos.

Resumo

As leis do movimento de Newton podem ser aplicadas em várias situações para resolver problemas de movimento.
Alguns problemas conterão vários vetores de força atuando em direções diferentes em um objeto. Certifique-se de desenhar diagramas, resolver todos os vetores de força em componentes horizontais e verticais e desenhar um diagrama de corpo livre. Sempre analise a direção na qual um objeto acelera para que você possa determinar se\(F_{net} = ma\) ou\(F_{net} = 0 \).
A força normal em um objeto nem sempre é igual em magnitude ao peso do objeto. Se um objeto estiver acelerando, a força normal será menor ou maior que o peso do objeto. Além disso, se o objeto estiver em um plano inclinado, a força normal sempre será menor que o peso total do objeto.
Alguns problemas conterão várias grandezas físicas, como forças, aceleração, velocidade ou posição. Você pode aplicar conceitos de cinemática e dinâmica para resolver esses problemas de movimento.